2.6.1直角三角形的性质 课件(20张PPT)
文档属性
| 名称 | 2.6.1直角三角形的性质 课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 617.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 09:04:45 | ||
图片预览



文档简介
(共20张PPT)
直角三角形的性质
直角三角形的性质
浙教版 八上
目录
目录
直角三角形
01
斜中线性质
03
直角三角形锐角互余
02
直角三角形中的30度
04
导入新课
内角三兄弟之争
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大! ”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了......”“为什么 ” 老二很纳闷.你知道其中的道理吗
导入新课
老大的度数为90°,老二若是比老大的度数大,那么老二的度数要大于90°,而三角形的内角和为180°相互矛盾,因而是不可能的.
在这个家里,我是永远的老大.
讲授新课
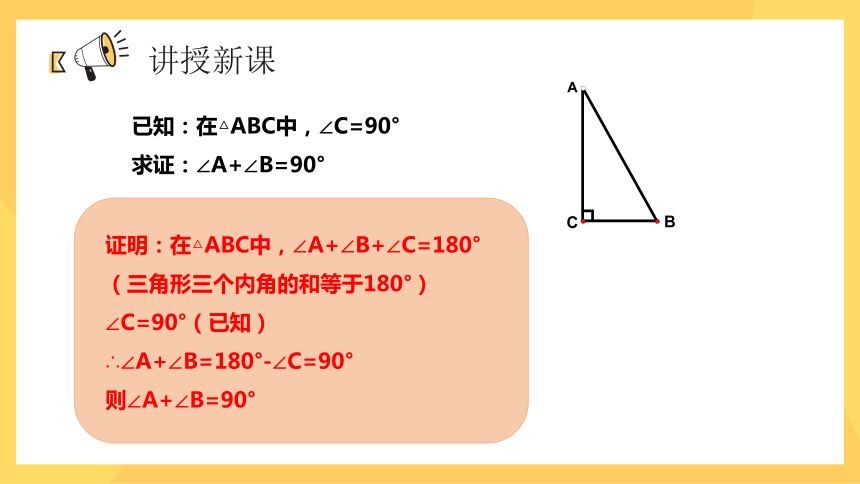
已知:在△ABC中,∠C=90°
求证:∠A+∠B=90°
证明:在△ABC中,∠A+∠B+∠C=180°
(三角形三个内角的和等于180°)
∠C=90°(已知)
∴∠A+∠B=180°-∠C=90°
则∠A+∠B=90°
合作学习
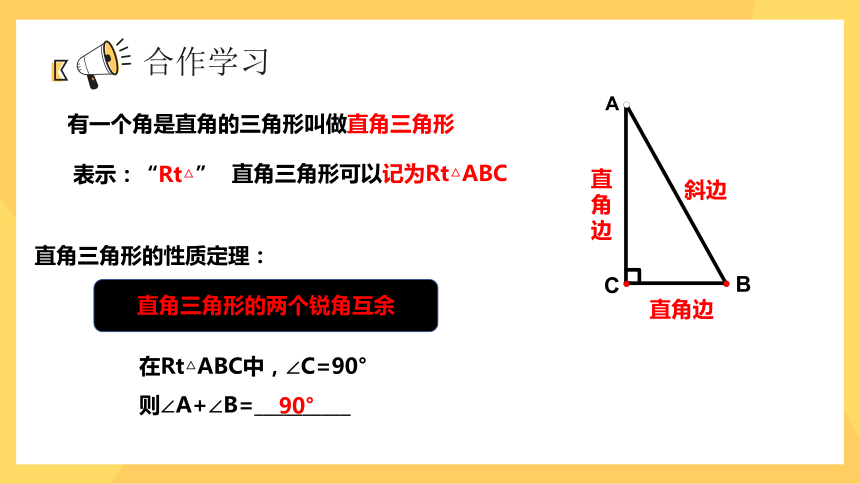
有一个角是直角的三角形叫做直角三角形
表示:
“Rt△”
直角三角形可以记为Rt△ABC
斜边
直
角
边
直角边
直角三角形的两个锐角互余
直角三角形的性质定理:
在Rt△ABC中,∠C=90°
则∠A+∠B=__________
90°
巩固练习
已知直角三角形两个锐角的度数之比为3:2,求这两个锐角的度数。
解:∵三角形内角和是180°,直角三角形中有一个角是90°
∴直角三角形的两个锐角度数的和是90°,
又3+2=5,
∴这两个锐角分别为:90°×=54°;
90°×=36°,
答:这个三角形两个锐角的度数分别是 54°,36°.
讲授新课
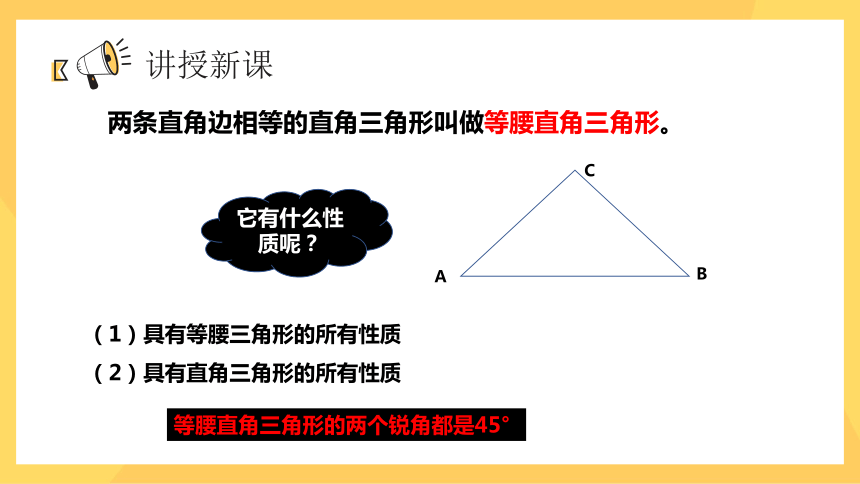
两条直角边相等的直角三角形叫做等腰直角三角形。
它有什么性质呢?
(1)具有等腰三角形的所有性质
(2)具有直角三角形的所有性质
等腰直角三角形的两个锐角都是45°
C
A
B
巩固练习
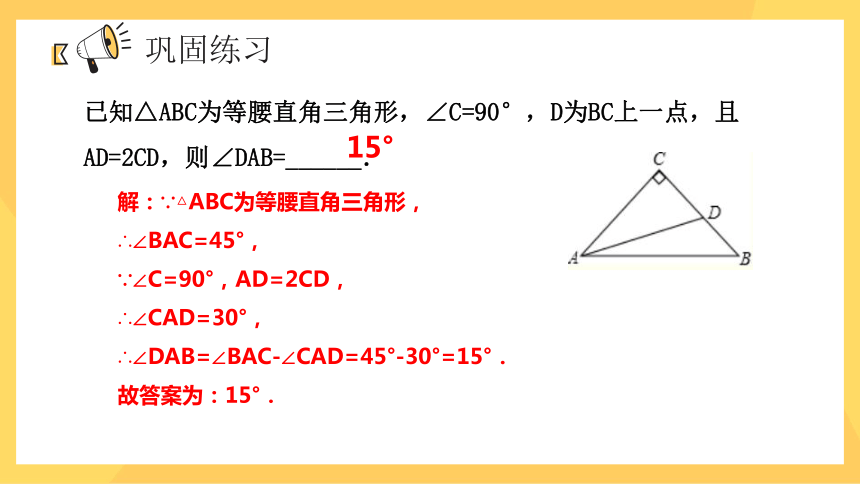
已知△ABC为等腰直角三角形,∠C=90°,D为BC上一点,且AD=2CD,则∠DAB=______.
解:∵△ABC为等腰直角三角形,
∴∠BAC=45°,
∵∠C=90°,AD=2CD,
∴∠CAD=30°,
∴∠DAB=∠BAC-∠CAD=45°-30°=15°.
故答案为:15°.
15°
探究学习
已知:如图,D是Rt△ABC斜边AB上的一点,BD=CD,求证:AD=CD
证明:∵∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,
∵BD=CD,∴∠B=∠BCD,
∴∠A=∠ACD(等角的余角相等),
∴AD=CD.
D
合作学习
直角三角形还有以下性质定理:
直角三角形斜边上的中线等于斜边的一半
数学语言表述为:
在Rt△ABC中,
∵CD是斜边AB上的中线
∴CD=AD=BD=AB
D
例题讲解
例1 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少米
直角三角形斜边上的中线等于斜边的一半
直角三角形的两个锐角互余
A
B
C
D
30°
有一个角为60°的等腰三角形是等边三角形
解:作Rt△ABC的斜边上的中线CD,
则CD=AD=AB=×200=100(m)
(_________________________________________)
∵∠B=30°
∴∠A=90°-∠B=60°(_______________________________)
∴△ADC是等边三角形(为什么?)
∴AC=AD=100(m)
答:这名滑雪运动员的高度下降了100m。
合作学习
直角三角形还有以下性质定理:
在直角三角形中,30°角所对的直角边等于斜边的一半
数学语言表述为:
在Rt△ABC中,∠A=30°,
∴BC=AB
30°
例2:如图,∠C=∠D=90°,AD,BC相交于点E.∠CAE与∠DBE有什么关系 为什么
解:在Rt△ACE中,
∠CAE=90°- ∠AEC
在Rt△BDE中,
∠DBE=90°- ∠BED
∵∠AEC= ∠BED
∴∠CAE= ∠DBE
C
D
E
A
B
例题讲解
例题讲解
例3:右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m, ∠A= 30 °,立柱BC、DE要多长?
B
A
D
C
E
解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=AB,DE=AD,
∴BC=×7.4=3.7(m)
又AD=AB=BC
∴DE=AD=×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.
举一反三
1.如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD的长是( )
A.20 B.10 C.5 D.
【解析】∵在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,
∴CD=×AB=5,故选C.
C
举一反三
2.如图,直角三角形ABC中,O是BC中点且BD⊥CD,试说明AO与OD的关系.
解:AO=DO,
理由是:∵∠BAC=90°,O为BC中点,
∴AO=BC,
∵BD⊥CD,
∴∠BDC=90°,
∵O为BC中点,
∴DO=BC,
∴AO=DO
举一反三
3. 如图,已知AD⊥BD,AC⊥BC,E为AB的中点.
试判断DE与CE是否相等,并给出证明.
A
B
C
D
E
解:∵AD⊥BD,AC⊥BC,E是AB的中点
∴DE= AB,CE= AB
∴DE=CE
举一反三
4.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形。
解: 连结AD,∵AB=AC,∠BAC=90°,D为BC的中点
∴AD⊥BC ,BD=AD,
∴∠B=∠DAC=45°
又BE=AF,
∴△BDE≌△ADF(SAS)
∴ED=FD,∠BDE=∠ADF
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°
∴△DEF为等腰直角三角形
举一反三
4.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论。
解:如图所示,连结AD, ∵ AB=AC,∠BAC=90°,D为BC的中点
∴AD=BD,AD⊥BC, ∴ ∠DAC=∠ABD=45°
∴ ∠DAF=∠DBE=135°
又AF=BE,
∴ △DAF≌△DBE
∴ FD=ED,∠FDA=∠EDB
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°
∴ △DEF仍为等腰直角三角形
直角三角形的性质
直角三角形的性质
浙教版 八上
目录
目录
直角三角形
01
斜中线性质
03
直角三角形锐角互余
02
直角三角形中的30度
04
导入新课
内角三兄弟之争
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大! ”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了......”“为什么 ” 老二很纳闷.你知道其中的道理吗
导入新课
老大的度数为90°,老二若是比老大的度数大,那么老二的度数要大于90°,而三角形的内角和为180°相互矛盾,因而是不可能的.
在这个家里,我是永远的老大.
讲授新课
已知:在△ABC中,∠C=90°
求证:∠A+∠B=90°
证明:在△ABC中,∠A+∠B+∠C=180°
(三角形三个内角的和等于180°)
∠C=90°(已知)
∴∠A+∠B=180°-∠C=90°
则∠A+∠B=90°
合作学习
有一个角是直角的三角形叫做直角三角形
表示:
“Rt△”
直角三角形可以记为Rt△ABC
斜边
直
角
边
直角边
直角三角形的两个锐角互余
直角三角形的性质定理:
在Rt△ABC中,∠C=90°
则∠A+∠B=__________
90°
巩固练习
已知直角三角形两个锐角的度数之比为3:2,求这两个锐角的度数。
解:∵三角形内角和是180°,直角三角形中有一个角是90°
∴直角三角形的两个锐角度数的和是90°,
又3+2=5,
∴这两个锐角分别为:90°×=54°;
90°×=36°,
答:这个三角形两个锐角的度数分别是 54°,36°.
讲授新课
两条直角边相等的直角三角形叫做等腰直角三角形。
它有什么性质呢?
(1)具有等腰三角形的所有性质
(2)具有直角三角形的所有性质
等腰直角三角形的两个锐角都是45°
C
A
B
巩固练习
已知△ABC为等腰直角三角形,∠C=90°,D为BC上一点,且AD=2CD,则∠DAB=______.
解:∵△ABC为等腰直角三角形,
∴∠BAC=45°,
∵∠C=90°,AD=2CD,
∴∠CAD=30°,
∴∠DAB=∠BAC-∠CAD=45°-30°=15°.
故答案为:15°.
15°
探究学习
已知:如图,D是Rt△ABC斜边AB上的一点,BD=CD,求证:AD=CD
证明:∵∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,
∵BD=CD,∴∠B=∠BCD,
∴∠A=∠ACD(等角的余角相等),
∴AD=CD.
D
合作学习
直角三角形还有以下性质定理:
直角三角形斜边上的中线等于斜边的一半
数学语言表述为:
在Rt△ABC中,
∵CD是斜边AB上的中线
∴CD=AD=BD=AB
D
例题讲解
例1 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少米
直角三角形斜边上的中线等于斜边的一半
直角三角形的两个锐角互余
A
B
C
D
30°
有一个角为60°的等腰三角形是等边三角形
解:作Rt△ABC的斜边上的中线CD,
则CD=AD=AB=×200=100(m)
(_________________________________________)
∵∠B=30°
∴∠A=90°-∠B=60°(_______________________________)
∴△ADC是等边三角形(为什么?)
∴AC=AD=100(m)
答:这名滑雪运动员的高度下降了100m。
合作学习
直角三角形还有以下性质定理:
在直角三角形中,30°角所对的直角边等于斜边的一半
数学语言表述为:
在Rt△ABC中,∠A=30°,
∴BC=AB
30°
例2:如图,∠C=∠D=90°,AD,BC相交于点E.∠CAE与∠DBE有什么关系 为什么
解:在Rt△ACE中,
∠CAE=90°- ∠AEC
在Rt△BDE中,
∠DBE=90°- ∠BED
∵∠AEC= ∠BED
∴∠CAE= ∠DBE
C
D
E
A
B
例题讲解
例题讲解
例3:右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m, ∠A= 30 °,立柱BC、DE要多长?
B
A
D
C
E
解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=AB,DE=AD,
∴BC=×7.4=3.7(m)
又AD=AB=BC
∴DE=AD=×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.
举一反三
1.如图,在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,则CD的长是( )
A.20 B.10 C.5 D.
【解析】∵在Rt△ABC中,∠ACB=90°,AB=10,CD是AB边上的中线,
∴CD=×AB=5,故选C.
C
举一反三
2.如图,直角三角形ABC中,O是BC中点且BD⊥CD,试说明AO与OD的关系.
解:AO=DO,
理由是:∵∠BAC=90°,O为BC中点,
∴AO=BC,
∵BD⊥CD,
∴∠BDC=90°,
∵O为BC中点,
∴DO=BC,
∴AO=DO
举一反三
3. 如图,已知AD⊥BD,AC⊥BC,E为AB的中点.
试判断DE与CE是否相等,并给出证明.
A
B
C
D
E
解:∵AD⊥BD,AC⊥BC,E是AB的中点
∴DE= AB,CE= AB
∴DE=CE
举一反三
4.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形。
解: 连结AD,∵AB=AC,∠BAC=90°,D为BC的中点
∴AD⊥BC ,BD=AD,
∴∠B=∠DAC=45°
又BE=AF,
∴△BDE≌△ADF(SAS)
∴ED=FD,∠BDE=∠ADF
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°
∴△DEF为等腰直角三角形
举一反三
4.已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论。
解:如图所示,连结AD, ∵ AB=AC,∠BAC=90°,D为BC的中点
∴AD=BD,AD⊥BC, ∴ ∠DAC=∠ABD=45°
∴ ∠DAF=∠DBE=135°
又AF=BE,
∴ △DAF≌△DBE
∴ FD=ED,∠FDA=∠EDB
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°
∴ △DEF仍为等腰直角三角形
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
