第2章 特殊三角形章末测试卷（含解析）

特殊三角形章末测试卷
考试时间：60分钟；满分：100分
姓名：___________班级：___________考号：___________
考卷信息：
本卷试题共23题，单选10题，填空6题，解答7题，满分100分，限时60分钟，本卷题型针对性较高，覆盖面广，选题有深度，可衡量学生掌握本章内容的具体情况！
一．选择题（共10小题，满分30分，每小题3分）
1．（2022秋 徐州期中）下列四个浏览器的图标中，属于轴对称图形的是（　　）
A． B． C． D．
2．（2022 昆明一模）如图，BE＝CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还要添加一个条件是（　　）
A．AB＝DC B．∠A＝∠D C．∠B＝∠C D．AE＝BF
3．（2022春 富阳区期末）用反证法证明：“一个三角形中，至少有一个内角大于或等于60°”．应假设（　　）
A．一个三角形中没有一个角大于或等于60°
B．一个三角形中至少有一个角小于60°
C．一个三角形中三个角都大于等于60°
D．一个三角形中有一个角大于等于60°
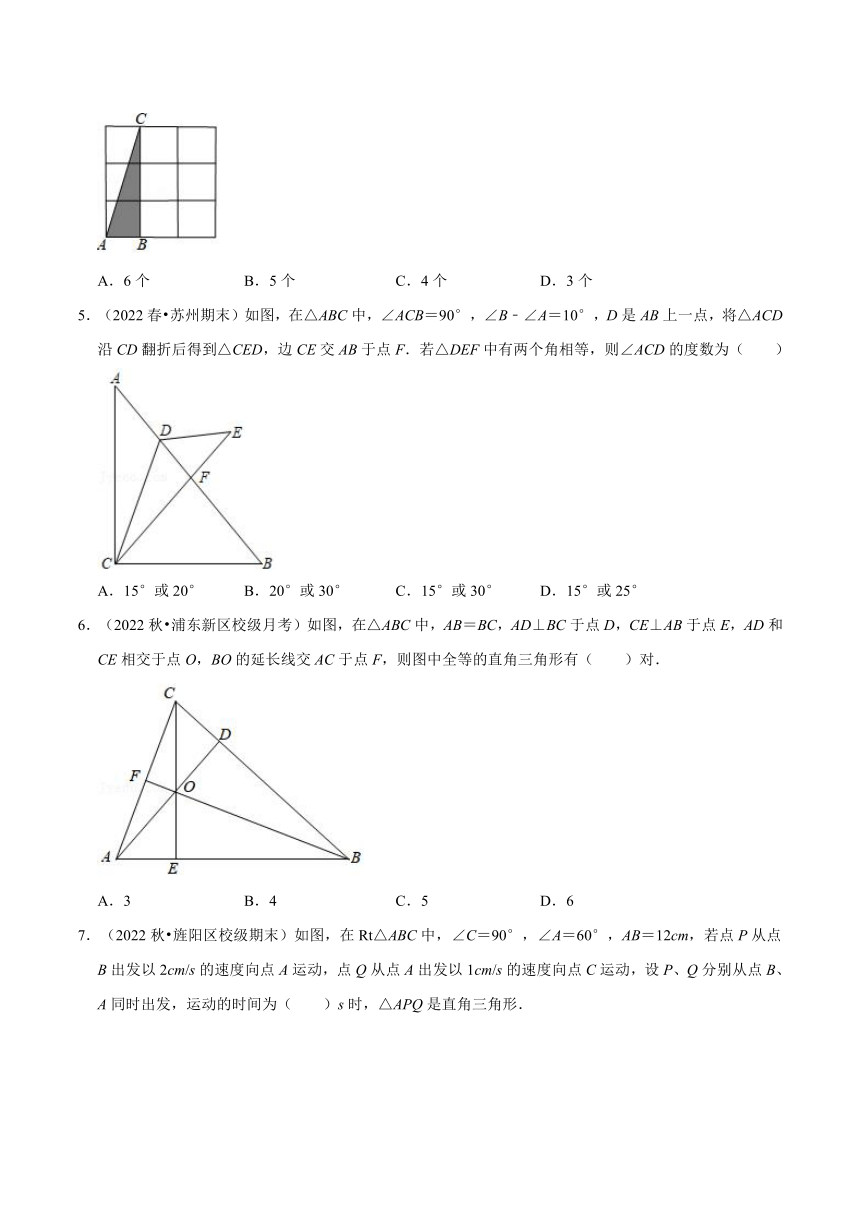
4．（2022秋 仓山区期末）如图，在3×3的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的△ABC为格点三角形，在图中最多能画出（　　）个格点三角形与△ABC成轴对称．
A．6个 B．5个 C．4个 D．3个
5．（2022春 苏州期末）如图，在△ABC中，∠ACB＝90°，∠B﹣∠A＝10°，D是AB上一点，将△ACD沿CD翻折后得到△CED，边CE交AB于点F．若△DEF中有两个角相等，则∠ACD的度数为（　　）
A．15°或20° B．20°或30° C．15°或30° D．15°或25°
6．（2022秋 浦东新区校级月考）如图，在△ABC中，AB＝BC，AD⊥BC于点D，CE⊥AB于点E，AD和CE相交于点O，BO的延长线交AC于点F，则图中全等的直角三角形有（　　）对．
A．3 B．4 C．5 D．6
7．（2022秋 旌阳区校级期末）如图，在Rt△ABC中，∠C＝90°，∠A＝60°，AB＝12cm，若点P从点B出发以2cm/s的速度向点A运动，点Q从点A出发以1cm/s的速度向点C运动，设P、Q分别从点B、A同时出发，运动的时间为（　　）s时，△APQ是直角三角形．
A．2.4 B．3 C．2.4或3 D．3或4.8
8．（2022秋 江夏区期末）如图，△ABC中，∠CAB＝∠CBA＝48°，点O为△ABC内一点，∠OAB＝12°，∠OBC＝18°，则∠ACO+∠AOB＝（　　）
A．190° B．195° C．200° D．210°
9．（2022秋 万州区期末）Rt△ABC和Rt△CDE按如图所示的位置摆放，顶点B、C、D在同一直线上，AC＝CE，∠B＝∠D＝90°，AB＞BC．将Rt△ABC沿着AC翻折，得到Rt△AB'C，将Rt△CDE沿着CE翻折，得Rt△CD'E，点B、D的对应点B'、D'与点C恰好在同一直线上，若AC＝13，BD＝17，则B'D'的长度为（　　）
A．7 B．6 C．5 D．4
10．（2022春 洪雅县期末）在直角三角形ABC中，∠C＝90°，∠BAC的平分线AD交BC于点D，∠ABC的平分线BE交AC于点E，AD、BE相交于点F，过点D作DG∥AB，过点B作BG⊥DG交DG于点G．有以下结论：①∠AFB＝135°；②∠BDG＝2∠CBE；③BC平分∠ABG；④∠BEC＝∠FBG．其中正确的个数是（　　）
A．1个 B．2个 C．3个 D．4个
二．填空题（共6小题，满分18分，每小题3分）
11．（2022春 锦江区校级期末）已知△ABC为等边三角形，AB＝10，M在AB边所在直线上，点N在AC边所在直线上，且MN＝MC，若AM＝16，则CN的长为 　 　．
12．（2022春 菏泽期末）如图，在Rt△ABC中，∠C＝90°，两锐角的角平分线交于点P，点E、F分别在边BC、AC上，且都不与点C重合，若∠EPF＝45°，连接EF，当AC＝6，BC＝8，AB＝10时，则△CEF的周长为 　 　．
13．（2022春 罗湖区校级期中）已知一个等腰三角形腰上的高与底边的夹角为37°，则这个等腰三角形的顶角等于　 　度．
14．（2022秋 余姚市期末）如图，∠BAC＝90°，点B是射线AM上的一个动点．点C是射线AN上一个动点，且线段BC的长度不变，点D是点A关于直线BC的对称点，连接AD，若2AD＝BC，则∠ABD的度数是　 　．
15．（2022秋 江夏区期末）在Rt△ABC中，∠BAC＝90°，BD、CE分别平分∠ABC和∠ACB且BD、CE相交于点O，过点O作FO⊥BD交AB于点F，连FD．若∠A﹣∠ACB＝α（0°＜α＜60°），则∠AFD＝　 　．
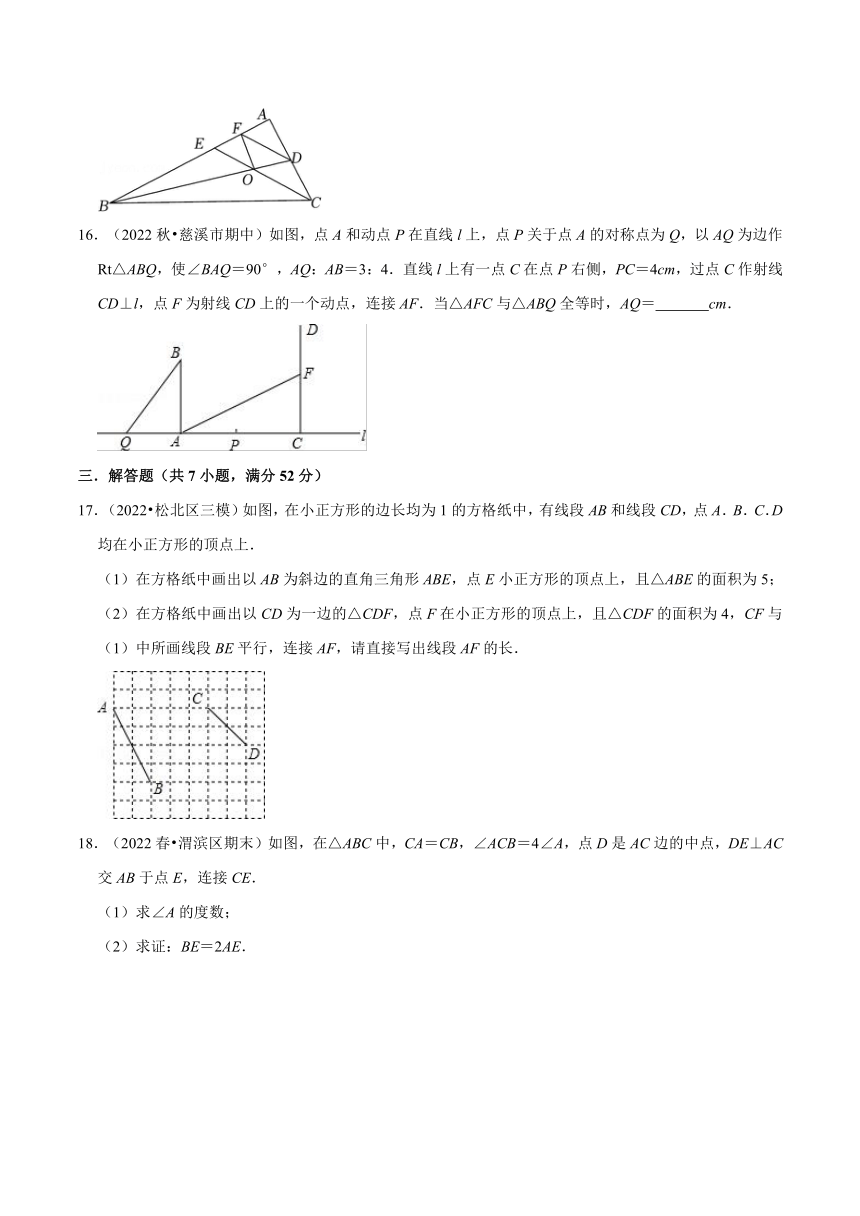
16．（2022秋 慈溪市期中）如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ＝90°，AQ：AB＝3：4．直线l上有一点C在点P右侧，PC＝4cm，过点C作射线CD⊥l，点F为射线CD上的一个动点，连接AF．当△AFC与△ABQ全等时，AQ＝　 　cm．
三．解答题（共7小题，满分52分）
17．（2022 松北区三模）如图，在小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A．B．C．D均在小正方形的顶点上．
（1）在方格纸中画出以AB为斜边的直角三角形ABE，点E小正方形的顶点上，且△ABE的面积为5；
（2）在方格纸中画出以CD为一边的△CDF，点F在小正方形的顶点上，且△CDF的面积为4，CF与（1）中所画线段BE平行，连接AF，请直接写出线段AF的长．
18．（2022春 渭滨区期末）如图，在△ABC中，CA＝CB，∠ACB＝4∠A，点D是AC边的中点，DE⊥AC交AB于点E，连接CE．
（1）求∠A的度数；
（2）求证：BE＝2AE．
19．（2022秋 永定县校级期中）（1）如图1，△ABC中，∠BAC＝90°，AB＝AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD＝DE+CE．
（2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．
20．（2022秋 咸丰县期末）如图，等边△ABC的边长为12cm，D为AC边上一动点，E为AB延长线上一动点，DE交CB于点P，点P为DE中点
（1）求证：CD＝BE；
（2）若DE⊥AC，求BP的长．
21．（2022秋 临河区期末）在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且AE＝BD，
（1）当点E为AB的中点时，如图1，求证：EC＝ED；
（2）当点E不是AB的中点时，如图2，过点E作EF∥BC，求证：△AEF是等边三角形；
（3）在第（2）小题的条件下，EC与ED还相等吗，请说明理由．
22．（2022春 无锡期中）如图①，△ABC的角平分线BD、CE相交于点P．
（1）如果∠A＝80°，求∠BPC的度数；
（2）如图②，过P点作直线MN，分别交AB和AC于点M和N，且MN平行于BC，试求∠MPB+∠NPC的度数（用含∠A的代数式表示）；
（3）将（2）中的直线MN绕点P旋转，分别交线段AB于点M（不与A、B重合），交直线AC于N，试探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明理由．
23．（2022秋 婺城区校级期末）已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1，h2，h3，△ABC的高为h．回答以下问题：
（1）如图（1），若点P在一边BC上，此时h3＝0，可得结论　 　（结论用h1，h2，h3，h的关系式表示）
（2）如图（2），当点P在△ABC内，此时可得结论　 　（结论用h1，h2，h3，h的关系式表示）
（3）如图（3），当点P在△ABC外，上述结论是否成立？若成立，请予以证明；若不成立，h1，h2，h3和h之间又有怎样的关系，并说明理由．
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．（2022秋 徐州期中）下列四个浏览器的图标中，属于轴对称图形的是（　　）
A． B． C． D．
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【详解】解：A、不是轴对称图形，故此选项不符合题意；
B、不是轴对称图形，故此选项不符合题意；
C、不是轴对称图形，故此选项不符合题意；
D、是轴对称图形，故此选项符合题意；
故选：D．
【点睛】此题主要考查了轴对称图形，关键是掌握轴对称图形概念．
2．（2022 昆明一模）如图，BE＝CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还要添加一个条件是（　　）
A．AB＝DC B．∠A＝∠D C．∠B＝∠C D．AE＝BF
【分析】根据垂直定义求出∠CFD＝∠AEB＝90°，再根据全等三角形的判定定理推出即可．
【详解】解：条件是AB＝CD，
理由是：∵AE⊥BC，DF⊥BC，
∴∠CFD＝∠AEB＝90°，
在Rt△ABE和Rt△DCF中，
，
∴Rt△ABE≌Rt△DCF（HL），
故选：A．
【点睛】本题考查了全等三角形的判定定理的应用，能灵活运用全等三角形的判定定理进行推理是解此题的关键．
3．（2022春 富阳区期末）用反证法证明：“一个三角形中，至少有一个内角大于或等于60°”．应假设（　　）
A．一个三角形中没有一个角大于或等于60°
B．一个三角形中至少有一个角小于60°
C．一个三角形中三个角都大于等于60°
D．一个三角形中有一个角大于等于60°
【分析】根据反证法的步骤，假设的命题肯定不成立．从这一点出发，一一判断即可．
【详解】解：要证明原命题成立，则反证法假设的命题肯定不成立．从这一点出发，可以排除B，D这两个选项；反证法的核心是假设出原命题的相反面（或者说除原命题外的其他情况），证明假设的命题不成立，进而间接的证明原命题成立！原命题中出现“至少有一个”，则其对立面应该是“没有”、“不存在”、“没有一个”，所以应假设：一个三角形中没有一个角大于或等于60°
故选：A．
【点睛】本题考查反证法，解题的关键是作为反证法的步骤，属于中考常考题型．
4．（2022秋 仓山区期末）如图，在3×3的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的△ABC为格点三角形，在图中最多能画出（　　）个格点三角形与△ABC成轴对称．
A．6个 B．5个 C．4个 D．3个
【分析】根据网格结构分别确定出不同的对称轴，然后作出轴对称三角形即可得解
【详解】解：如图，最多能画出6个格点三角形与△ABC成轴对称．
故选：A．
【点睛】本题考查了利用轴对称变换作图，熟练掌握网格结构并准确找出对应点的位置是解题的关键，本题难点在于确定出不同的对称轴．
5．（2022春 苏州期末）如图，在△ABC中，∠ACB＝90°，∠B﹣∠A＝10°，D是AB上一点，将△ACD沿CD翻折后得到△CED，边CE交AB于点F．若△DEF中有两个角相等，则∠ACD的度数为（　　）
A．15°或20° B．20°或30° C．15°或30° D．15°或25°
【分析】由三角形的内角和定理可求解∠A＝40°，设∠ACD＝x°，则∠CDF＝（40+x）°，∠ADC＝（140﹣x）°，由折叠可知：∠ADC＝∠CDE，∠E＝∠A＝40°，可分三种情况：当∠DFE＝∠E＝40°时；当∠FDE＝∠E＝40°时；当∠DFE＝∠FDE时，根据∠ADC＝∠CDE列方程，解方程可求解x值，即可求解．
【详解】解：在△ABC中，∠ACB＝90°，
∴∠B+∠A＝90°，
∵∠B﹣∠A＝10°，
∴∠A＝40°，∠B＝50°，
设∠ACD＝x°，则∠CDF＝（40+x）°，∠ADC＝180°﹣40°﹣x°＝（140﹣x）°，
由折叠可知：∠ADC＝∠CDE，∠E＝∠A＝40°，
当∠DFE＝∠E＝40°时，
∵∠FDE+∠DFE+∠E＝180°，
∴∠FDE＝180°﹣40°﹣40°＝100°，
∴140﹣x＝100+40+x，
解得x＝0（不存在）；
当∠FDE＝∠E＝40°时，
∴140﹣x＝40+40+x，
解得x＝30，
即∠ACD＝30°；
当∠DFE＝∠FDE时，
∵∠FDE+∠DFE+∠E＝180°，
∴∠FDE，
∴140﹣x＝70+40+x，
解得x＝15，
即∠ACD＝15°，
综上，∠ACD＝15°或30°，
故选：C．
【点睛】本题主要考查直角三角形的性质，等腰三角形的性质，三角形的内角和定理，根据∠ADC＝∠CDE分三种情况列方程是解题的关键．
6．（2022秋 浦东新区校级月考）如图，在△ABC中，AB＝BC，AD⊥BC于点D，CE⊥AB于点E，AD和CE相交于点O，BO的延长线交AC于点F，则图中全等的直角三角形有（　　）对．
A．3 B．4 C．5 D．6
【分析】全等三角形有△ABF≌△CBF，△ADB≌△CEB，△COD≌△AOE，△COF≌△AOF，△ADC≌△CEA，△EOB≌△DOB，根据全等三角形的判定和性质定理证明即可．
【详解】解：全等三角形有△ABF≌△CBF，△ADB≌△CEB，△COD≌△AOE，△COF≌△AOF，△ADC≌△CEA，△EOB≌△DOB，共6对，
理由是：∵AD⊥BC，CE⊥AB，
∴∠CEB＝∠ADB＝90°，∠AEC＝∠CDA＝90°，
在△ADB和△CEB中，
，
∴△ADB≌△CEB（AAS），
∴AD＝CE，BD＝BE，∠DCO＝∠EAO，
∵AB＝CB，
∴BC﹣BD＝AB﹣BE，
即CD＝AE，
在△CDO和△AEO中，
，
∴△CDO≌△AEO（ASA），
∴CO＝AO，DO＝EO，
在△COB和△AOB中，
，
∴△COB≌△AOB（SSS），
∴∠CBF＝∠ABF，
在△ABF和△CBF中，
，
∴△ABF≌△CBF（SAS），
∴CF＝AF，
在Rt△AFO和Rt△CFO中，
，
∴Rt△AFO≌Rt△CFO（HL），
同理：△ADC≌△CEA（HL），
在△EOB和△DOB中，
，
∴△EOB≌△DOB（SSS）
故选：D．
【点睛】本题考查了全等三角形的性质和判定，能正确运用全等三角形的性质和判定定理进行推理是解此题的关键，注意：①全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有HL；②全等三角形的对应边相等，对应角相等．
7．（2022春 交城县期中）勾股定理是一个古老的数学定理，它有很多种证明方法，如所示四幅几何图形中，不能用于证明勾股定理的是（　　）
A． B．
C． D．
【分析】用几个全等的直角三角形拼成一个规则的图形，然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理．
【详解】解：A．根据图形可知：
＝2ab+b2﹣2ab+a2
＝a2+b2，
∵，
∴a2+b2＝c2；故A选项不符合题意；
B．不能用于证明勾股定理，故B选项符合题意；
C．根据图形可知：S大正方形＝4ab+c2＝2ab+c2，
S大正方形＝（a+b）2＝a2+2ab+b2，
∴2ab+c2＝a2+2ab+b2，
∴a2+b2＝c2，故C选项不符合题意；
D．根据图形可知：S大正方形＝c2，
S大正方形（b+b+a）×b（a+b+a）×a﹣2ab＝a2+b2，
∴a2+b2＝c2，故D选项不符合题意，
故选：B．
【点睛】本题考查了勾股定理的证明及其应用，掌握勾股定理是解本题的关键．
8．（2022秋 江夏区期末）如图，△ABC中，∠CAB＝∠CBA＝48°，点O为△ABC内一点，∠OAB＝12°，∠OBC＝18°，则∠ACO+∠AOB＝（　　）
A．190° B．195° C．200° D．210°
【分析】根据已知易证CA＝CB，所以想到等腰三角形的三线合一性质，过点C作CD⊥AB，垂足为D，延长BO交CD与点P，然后连接AP，易证∠CAP＝∠CBP＝18°，从而求出∠PAO＝18°，再利用三角形的外角求出∠POA的度数，放在直角三角形中求出∠ACP的度数，进而证△ACP≌△AOP，可得AC＝AO，最后放在等腰三角形ACO中求出∠ACO即可．
【详解】解：过点C作CD⊥AB，垂足为D，延长BO交CD与点P，连接AP，
∵∠OBC＝18°，∠CBA＝48°，
∴∠ABP＝∠CBA﹣∠OBC＝30°，
∵∠CAB＝∠CBA＝48°，
∴CA＝CB，
∵CD⊥AB，
∴CD是AB的垂直平分线，
∴PA＝PB，
∴∠PAB＝∠PBA＝30°，
∴∠CAP＝∠CAB﹣∠PAB＝18°，
∵∠AOP是△AOB的一个外角，
∴∠AOP＝∠OAB+∠OBA＝42°，
∵∠CDA＝90°，
∴∠ACD＝90°﹣∠CAD＝42°，
∴∠AOP＝∠ACD，
∵∠PAB＝30°，∠OAB＝12°，
∴∠PAO＝∠PAB﹣∠OAB＝18°，
∴∠CAP＝∠OAP，
∵AP＝AP，
∴△ACP≌△AOP（AAS），
∴AC＝AO，
∵∠CAO＝∠CAP+∠OAP＝36°，
∴∠ACO＝∠AOC＝72°，
∵∠AOB＝180°﹣∠OAB﹣∠OBA＝138°，
∴∠ACO+∠AOB＝210°，
故选：D．
【点睛】本题考查了等腰三角形的性质，三角形内角和定理，三角形的外角性质，全等三角形的判定与性质，利用等腰三角形的三线合一性质添加辅助线是解题的关键．
9．（2022秋 万州区期末）Rt△ABC和Rt△CDE按如图所示的位置摆放，顶点B、C、D在同一直线上，AC＝CE，∠B＝∠D＝90°，AB＞BC．将Rt△ABC沿着AC翻折，得到Rt△AB'C，将Rt△CDE沿着CE翻折，得Rt△CD'E，点B、D的对应点B'、D'与点C恰好在同一直线上，若AC＝13，BD＝17，则B'D'的长度为（　　）
A．7 B．6 C．5 D．4
【分析】根据翻折的性质证明△BAC≌ECD，可得BC＝DE，AC＝CE＝13，然后根据勾股定理可以解决问题．
【详解】解：由翻折可知：∠ACB＝∠ACB′，∠ECD＝∠ECD′，
∵∠ACB+∠ACB′+∠ECD+∠ECD′＝180°，
∴∠ACB+∠ECD＝90°，
∵∠ACB+∠BAC＝90°，
∴∠BAC＝∠ECD，
在△BAC和ECD中，
，
∴△BAC≌ECD（AAS），
∴BC＝DE，AC＝CE＝13，
在RtCDE中，根据勾股定理，得
CD2+DE2＝CE2，
∴（17﹣BC）2+BC2＝132，
解得BC＝5或BC＝12（舍去），
∴B′C＝5，CD＝17﹣5＝12，
∴B′D′＝CD′﹣B′C＝12﹣5＝7．
故选：A．
【点睛】本题考查了翻折变换，全等三角形的判定与性质，解决本题的关键是得到∠ACE＝90°．
10．（2022春 洪雅县期末）在直角三角形ABC中，∠C＝90°，∠BAC的平分线AD交BC于点D，∠ABC的平分线BE交AC于点E，AD、BE相交于点F，过点D作DG∥AB，过点B作BG⊥DG交DG于点G．有以下结论：①∠AFB＝135°；②∠BDG＝2∠CBE；③BC平分∠ABG；④∠BEC＝∠FBG．其中正确的个数是（　　）
A．1个 B．2个 C．3个 D．4个
【分析】由三角形的内角和与角平分线的定义求∠AFB，由DG∥AB和BE平分∠ABC判断②，结合DG⊥DG求∠GBC与∠ABC的关系判断③，由三角形的内角和与平行线的性质判断④．
【详解】解：∵AD平分∠BAC，BE平分∠ABC，
∴∠BAF＝∠CAF∠BAC，∠FBA＝∠CBE∠ABC，
∵∠C＝90°，
∴∠BAC+∠ABC＝180°﹣90°＝90°，
∴∠FAB+∠FBA（∠BAC+∠ABC）＝45°，
∴∠AFB＝180°﹣（∠FAB+∠FBA）＝180°﹣45°＝135°，故①正确，符合题意；
∵DG∥AB，
∴∠BDG＝∠ABC，
∵∠CBE∠ABC，
∴∠BDG＝2∠CBE，故②正确，符合题意；
∵BG⊥DG，
∴∠G＝90°，
∴∠GDB+∠GBD＝90°，
又∵∠GDB＝∠ABC，
∴∠ABC+∠GBD＝90°，无法判定∠GBD＝∠ABC，故③错误，不符合题意；
又∵∠BAC+∠ABC＝90°，
∴∠BAC＝∠GBD，
∵∠ABF＝∠EBC，
∴∠ABF+∠BAC＝∠EBC+∠GBD，
∴∠BEC＝∠EBG，故④正确，符合题意；
故选：C．
【点睛】本题考查了三角形的内角和与外角和、平行线的性质、垂直的定义和角平分线的定义，整体思想的应用是判断①的关键，解题的时候要多次应用等量代换．
二．填空题（共6小题，满分18分，每小题3分）
11．（2022春 锦江区校级期末）已知△ABC为等边三角形，AB＝10，M在AB边所在直线上，点N在AC边所在直线上，且MN＝MC，若AM＝16，则CN的长为 　4或36　．
【分析】分两种情形：①当点M在AB的延长线上时，作MD⊥AC于D．②当点M在BA的延长线上时，作MD⊥CN于D．分别求解即可．
【详解】解：由题意可知，BM＝AN＝6，
①如图，当点M在AB的延长线上时，作MD⊥AC于D．
在Rt△AMD中，
∵∠ADM＝90°，∠A＝60°，AM＝16，
∴ADAM＝8，
∴CD＝AC﹣AD＝2，
∵MN＝MC，MD⊥CN，
∴DN＝CD，
∴CN＝2CD＝4．
②如图，当点M在BA的延长线上时，作MD⊥CN于D，
在Rt△AMD中，
∵∠ADM＝90°，∠DAM＝60°，AM＝16，
∴ADAM＝8，
∴CD＝AD+AC＝18，
∵MN＝MC，MD⊥CN，
∴DN＝CD，
∴CN＝2CD＝36，
故答案为：4或36．
【点睛】本题考查等边三角形的性质，解直角三角形的应用，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线面构造直角三角形解决问题．
12．（2022春 菏泽期末）如图，在Rt△ABC中，∠C＝90°，两锐角的角平分线交于点P，点E、F分别在边BC、AC上，且都不与点C重合，若∠EPF＝45°，连接EF，当AC＝6，BC＝8，AB＝10时，则△CEF的周长为 　4　．
【分析】如图，过点P作PM⊥BC于M，PN⊥AC于N，PK⊥AB于K，在EB上取一点J，使得MJ＝FN，连接PJ．利用全等三角形的性质证明EF＝EM+FN，可得结论．
【详解】解：如图，过点P作PM⊥BC于M，PN⊥AC于N，PK⊥AB于K，在EB上取一点J，使得MJ＝FN，连接PJ．
∵BP平分∠BC，PA平分∠CAB，PM⊥BC，PN⊥AC，PK⊥AB，
∴PM＝PK，PK＝PN，
∴PM＝PN，
∵∠C＝∠PMC＝∠PNC＝90°，
∴四边形PMCN是矩形，
∴四边形PMCN是正方形，
∴CM＝PM，
∴∠MPN＝90°，
在△PMJ和△PNF中，
，
∴△PMJ≌△PNF（SAS），
∴∠MPJ＝∠FPN，PJ＝PF，
∴∠JPF＝∠MPN＝90°，
∵∠EPF＝45°，
∴∠EPF＝∠EPJ＝45°，
在△PEF和△PEJ中，
，
∴△PEF≌△PEJ（SAS），
∴EF＝EJ，
∴EF＝EM+FN，
∴△CEF的周长＝CE+EF+CF＝CE+EM+CF+FN＝2CM＝2PM，
∵S△ABC BC AC（AC+BC+AB） PM，
∴PM＝2，
∴△ECF的周长为4，
故答案为：4．
【点睛】本题考查角平分线的性质定理，正方形的判定，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，证明EF＝EM+FN是本题的突破点．
13．（2022春 罗湖区校级期中）已知一个等腰三角形腰上的高与底边的夹角为37°，则这个等腰三角形的顶角等于　74　度．
【分析】此题要分两种情况推论：
（1）设等腰三角形的顶角是钝角时，腰上的高在三角形的外部，根据三角形的内角和求解；
（2）设等腰三角形的顶角是锐角时，根据直角三角形的两个锐角互余，求得底角，再根据三角形的内角和是180°，得顶角的度数．
【详解】
解：如图
（1）顶角是钝角时，
∵等腰三角形腰上的高与底边的夹角为37°，
∴∠OCB＝37°，
∵OC⊥OB，
∴∠ABC＝90°﹣37°＝53°，
∴∠BAC＝180°﹣53°﹣53°＝74°，
即△ABC为锐角三角形，顶角是钝角这种情况不成立；
（2）顶角是锐角时，∠B＝90°﹣37°＝53°，
∠A＝180°﹣2×53°＝74°．
因此，顶角为74°．
故答案为：74．
【点睛】本题考查了等腰三角形的性质及三角形的内角和定理；本题考查分情况讨论，但要注意，假设顶角是钝角，但求出后却是锐角，所以一定要舍去．
14．（2022秋 余姚市期末）如图，∠BAC＝90°，点B是射线AM上的一个动点．点C是射线AN上一个动点，且线段BC的长度不变，点D是点A关于直线BC的对称点，连接AD，若2AD＝BC，则∠ABD的度数是　30°或150°　．
【分析】分两种情况，取BC的中点E，连接AE，DE，依据直角三角形斜边上中线的性质，即可得到△ADE是等边三角形，进而依据轴对称的性质得出∠ABD的度数．
【详解】解：分两种情况：
如图，当AB＞AC时，取BC的中点E，连接AE，DE，
则AE＝DEBC，
即BC＝2AE＝2DE，
又∵BC＝2AD，
∴AD＝AE＝DE，
∴△ADE是等边三角形，
∴∠AED＝60°，
又∵BC垂直平分AD，
∴∠AEC＝30°，
又∵BE＝AE，
∴∠ABC∠AEC＝15°，
∴∠ABD＝2∠ABC＝30°；
如图，当AB＜AC时，同理可得∠ACD＝30°，
又∵∠BAC＝∠BDC＝90°，
∴∠ABD＝150°，
故答案为：30°或150°．
【点睛】本题主要考查了轴对称的性质的运用，如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．
15．（2022秋 江夏区期末）在Rt△ABC中，∠BAC＝90°，BD、CE分别平分∠ABC和∠ACB且BD、CE相交于点O，过点O作FO⊥BD交AB于点F，连FD．若∠A﹣∠ACB＝α（0°＜α＜60°），则∠AFD＝　45°α　．
【分析】连接AO，过O点作OM⊥AB于M，作ON⊥AC于点N，则∠FMO＝∠DNO＝90°，由∠BAC＝90°，∠BAC﹣∠ACB＝α知∠ACB＝90°﹣α，∠ABC＝α，∠ABDα，根据FO⊥BD可得∠AFO＝90°α，再证明△MOF≌△NOD求得∠OFD＝45°，进而可求解．
【详解】解：如图，连接AO，过O点作OM⊥AB于M，作ON⊥AC于点N，则∠FMO＝∠DNO＝90，
∵∠BAC＝90°，∠BAC﹣∠ACB＝α，
∴∠ACB＝90°﹣α，∠MON＝90°，
∴∠ABC＝α，
∵BD平分∠ABC，
∴∠ABDα，
∵FO⊥BD，
∴∠BOF＝∠FOD＝90°，
∴∠MOF＝∠NOD，∠AFO＝∠BOF+∠ABD＝90°α，
∵BO平分∠ABC，CO平分∠ACB，
∴AO平分∠BAC，
∴∠OAD＝45°，MO＝NO，
在△MOF和△NOD中，
，
∴△MOF≌△NOD（ASA），
∴OF＝OD，
∴∠OFD＝45°，
∴∠AFD＝∠AFO﹣∠OFD＝45°α，
故答案为：45°α．
【点睛】本题是三角形的综合问题，主要考查了等腰直角三角形，三角形的内角和定理、角平分线的性质、全等三角形的判定与性质等知识点，解题的关键是证明△MOF≌△NOD．
16．（2022秋 慈溪市期中）如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ＝90°，AQ：AB＝3：4．直线l上有一点C在点P右侧，PC＝4cm，过点C作射线CD⊥l，点F为射线CD上的一个动点，连接AF．当△AFC与△ABQ全等时，AQ＝　12或2或　cm．
【分析】根据直角三角形的全等的判定解答即可．
【详解】解：当P在A点的右侧时，AC不可能等于AQ，要使三角形全等，只能AC＝AB
要使△AFC与△ABQ全等，
则应满足，
∵AQ：AB＝3：4，AQ＝AP，PC＝4cm，
设AQ＝3x，AB＝4x，则有4x﹣3x＝4，
∴x＝4，
∴AQ＝12（cm），
当P在A点的左侧时，若AC＝AQ（即C，Q重合），可得AQ长为2；
若AC＝AB，可得AQ长为，
故答案为：12或2或．
【点睛】此题考查直角三角形的全等问题，关键是根据SAS证明三角形的全等．
三．解答题（共7小题，满分52分）
17．（2022 松北区三模）如图，在小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A．B．C．D均在小正方形的顶点上．
（1）在方格纸中画出以AB为斜边的直角三角形ABE，点E小正方形的顶点上，且△ABE的面积为5；
（2）在方格纸中画出以CD为一边的△CDF，点F在小正方形的顶点上，且△CDF的面积为4，CF与（1）中所画线段BE平行，连接AF，请直接写出线段AF的长．
【分析】（1）根据题意可知：AB，因为、、恰好构成以AB为斜边的直角三角形，由此画出图形即可；
（2）根据题意可知：CD，以CD为底，高为的三角形面积为4，由此画出图形，根据勾股定理求出AF的长即可．
【详解】解：（1）作图如下：
（2）AF5．
【点睛】此题考查勾股定理运用，三角形的面积计算方法，灵活利用数据之间的联系，结合图形解决问题．
18．（2022春 渭滨区期末）如图，在△ABC中，CA＝CB，∠ACB＝4∠A，点D是AC边的中点，DE⊥AC交AB于点E，连接CE．
（1）求∠A的度数；
（2）求证：BE＝2AE．
【分析】（1）设∠A的度数为x，则∠ACB＝4∠A＝4x，根据等腰三角形的性质得出∠B＝∠A＝x，根据三角形的内角和定理得出x+x+4x＝180°，再求出x即可；
（2）根据线段垂直平分线的性质得出AE＝CE，求出∠ECA＝∠A＝30°，求出∠BCE，再根据直角三角形的性质得出即可．
【详解】（1）解：设∠A的度数为x，则∠ACB＝4∠A＝4x，
∵AC＝BC，
∴∠B＝∠A＝x，
在△ABC中，∠A+∠B+∠ACB＝180°，
∴x+x+4x＝180°，
解得：x＝30°，
∴∠A＝30°，
答：∠A的度数是30°；
（2）证明：∵点D是AC边的中点，DE⊥AC，
∴AE＝CE
∴∠ECA＝∠A＝30°
又∠ACB＝4∠A＝120°，
∴∠BCE＝90°，
又∵∠B＝30°
∴BE＝2CE，
∴BE＝2AE．
【点睛】本题考查了线段垂直平分线性质，等腰三角形的性质，三角形内角和定理等知识点，能熟记线段垂直平分线上的点到线段两个端点的距离相等是解此题的关键．
19．（2022秋 永定县校级期中）（1）如图1，△ABC中，∠BAC＝90°，AB＝AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD＝DE+CE．
（2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．
【分析】根据已知利用AAS判定△ABD≌△CAE从而得到BD＝AE，AD＝CE，因为AE＝AD+DE，所以BD＝DE+CE；
根据已知利用AAS判定△ABD≌△CAE从而得到BD＝AE，AD＝CE，因为AD+AE＝BD+CE，所以BD＝DE﹣CE．
【详解】解：（1）∵∠BAC＝90°，BD⊥AE，CE⊥AE，
∴∠BDA＝∠AEC＝90°，
∵∠ABD+∠BAE＝90°，∠CAE+∠BAE＝90°
∴∠ABD＝∠CAE，
∵AB＝AC，
在△ABD和△CAE中，
∵，
∴△ABD≌△CAE（AAS），
∴BD＝AE，AD＝CE，
∵AE＝AD+DE，
∴BD＝DE+CE；
（2）BD＝DE﹣CE；
∵∠BAC＝90°，BD⊥AE，CE⊥AE，
∴∠BDA＝∠AEC＝90°，
∴∠ABD+∠DAB＝∠DAB+∠CAE，
∴∠ABD＝∠CAE，
∵AB＝AC，
在△ABD和△CAE中，
∵，
∴△ABD≌△CAE（AAS），
∴BD＝AE，AD＝CE，
∴AD+AE＝BD+CE，
∵DE＝BD+CE，
∴BD＝DE﹣CE．
【点睛】此题主要考查学生对全等三角形的判定方法的理解及运用，常用的判定方法有SSS，SAS，AAS等．这种类型的题目经常考到，要注意掌握．
20．（2022秋 咸丰县期末）如图，等边△ABC的边长为12cm，D为AC边上一动点，E为AB延长线上一动点，DE交CB于点P，点P为DE中点
（1）求证：CD＝BE；
（2）若DE⊥AC，求BP的长．
【分析】（1）作DF∥AB交BC于F，由等边三角形的性质得出∠A＝∠ABC＝∠C＝60°，由平行线的性质得出∠CDF＝∠A＝60°，∠DFC＝∠ABC＝60°，∠DFP＝∠EBP，证出△CDF是等边三角形，得出CD＝DF，由AAS证明△PDF≌△PEB，得出对应边相等DF＝BE，即可得出结论；
（2）由含30°角的直角三角形的性质得出ADAE，证出BP＝BE，得出BP＝BE＝CD，设BP＝x，则BE＝CD＝x，AD＝12﹣x，得出方程12+x＝2（12﹣x），解方程即可．
【详解】（1）证明：作DF∥AB交BC于F，如图所示：
∵△ABC是等边三角形，
∴∠A＝∠ABC＝∠C＝60°，
∵DF∥AB，
∴∠CDF＝∠A＝60°，∠DFC＝∠ABC＝60°，∠DFP＝∠EBP，
∴△CDF是等边三角形，
∴CD＝DF，
∵点P为DE中点，
∴PD＝PE，
在△PDF和△PEB中，，
∴△PDF≌△PEB（AAS），
∴DF＝BE，
∴CD＝BE；
（2）解：∵DE⊥AC，
∴∠ADE＝90°，
∴∠E＝90°﹣∠A＝30°，
∴ADAE，∠BPE＝∠ACB﹣∠E＝30°＝∠E，
∴BP＝BE，
由（1）得：CD＝BE，
∴BP＝BE＝CD，
设BP＝x，则BE＝CD＝x，AD＝12﹣x，
∵AE＝2AD，
∴12+x＝2（12﹣x），
解得：x＝4，
即BP的长为4．
【点睛】本题考查了全等三角形的判定与性质、等边三角形的判定与性质、平行线的性质、含30°角的直角三角形的性质等知识；本题综合性强，难度适中，证明三角形全等是解决问题的关键．
21．（2022秋 临河区期末）在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且AE＝BD，
（1）当点E为AB的中点时，如图1，求证：EC＝ED；
（2）当点E不是AB的中点时，如图2，过点E作EF∥BC，求证：△AEF是等边三角形；
（3）在第（2）小题的条件下，EC与ED还相等吗，请说明理由．
【分析】（1）根据等边三角形三线合一的性质可得∠ECB＝30°，∠ABC＝60°，根据AE＝EB＝BD，可得∠ECB∠ACB＝30°，∠EDB＝∠DEB∠ACB＝30°，根据等角对等边即可证得结论；
（2）根据平行线的性质证得∠AEF＝∠ABC＝60°，∠AFE＝∠C＝60°，即可证得结论；
（3）先求得BE＝FC，然后证得△DBE≌△EFC即可；
【详解】证明：（1）如图1，在等边△ABC中，AB＝BC＝AC，
∴∠ABC＝∠ACB＝∠A＝60°，
∵AE＝EB＝BD，
∴∠ECB∠ACB＝30°，∠EDB＝∠DEB∠ACB＝30°，
∴∠EDB＝∠ECB，
∴EC＝ED；
（2）如图2，∵EF∥BC，
∴∠AEF＝∠ABC＝60°，∠AFE＝∠C＝60°，
∴△AEF为等边三角形；
（3）EC＝ED；
理由：∵∠AEF＝∠ABC＝60°，
∴∠EFC＝∠DBE＝120°，
∵AB＝AC，AE＝AF，
∴AB﹣AE＝AC﹣AF，即BE＝FC，
在△DBE和△EFC中，
，
∴△DBE≌△EFC（SAS），
∴ED＝EC．
【点睛】本题考查了等边三角形的判定和性质性质，平行线的性质，三角形全等的判定和性质，熟练掌握性质和定理是解题的关键．
22．（2022春 无锡期中）如图①，△ABC的角平分线BD、CE相交于点P．
（1）如果∠A＝80°，求∠BPC的度数；
（2）如图②，过P点作直线MN，分别交AB和AC于点M和N，且MN平行于BC，试求∠MPB+∠NPC的度数（用含∠A的代数式表示）；
（3）将（2）中的直线MN绕点P旋转，分别交线段AB于点M（不与A、B重合），交直线AC于N，试探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明理由．
【分析】（1）利用角平分线的定义和三角形的内角和计算即可；
（2）利用角平分线的定义和三角形的内角和计算即可；
（3）利用角平分线的定义和三角形的内角和计算即可．
【详解】解：（1）∵∠BPC+∠PBC+∠PCB＝180°，
∴∠BPC＝180°﹣（∠PBC+∠PCB），
∵∠PBC，∠PCB，
∴∠PBC+∠PCB，
∵∠ABC+∠ACB+∠A＝180°，
∴∠ABC+∠ACB＝180°﹣∠A，
∴∠PBC+∠PCB°﹣∠A），
∵∠BPC＝180°﹣（∠PBC+∠PCB），
∴∠BPC＝180°
＝90°，
∵∠A＝80°，
∴∠BPC＝90°+40°＝130°；
（2）由（1）得，∠BPC＝90°∠A，
又∵∠BPC+∠MPB+∠NPC＝180°，
∴∠MPB+∠NPC＝180°﹣（90°∠A）＝90°∠A，
即∠MPB+∠NPC＝90°∠A；
（3）点M在线段AB上，点N在直线AC上，
所以分三种情况：
①点N在线段AC上时，如备用图1，
结论同（2），∠MPB+∠NPC＝90°∠A；
②点N在AC的延长线上时，如备用图2，
∵∠MPB+∠BPN＝180°，
∠BPN＝∠BPC﹣∠NPC，∠BPC＝90°，
∴∠MPB+∠BPC﹣∠NPC＝180°
∴∠MPB﹣∠NPC＝180°﹣∠BPC
＝90°∠A，
即∠MPB﹣∠NPC＝90°∠A；
③点N在CA的延长线上时，如备用图3，
∵∠MPB+∠NPC+∠BPC＝360°，
∴∠MPB+∠NPC＝360°﹣∠BPC
＝360°﹣（90°∠A）
＝270°∠A，
即∠MPB+∠NPC＝270°∠A．
【点睛】本题考查的是三角形内角和与角平分线，解题的关键是画出正确图形，会利用内角和表示角之间的关系．
23．（2022秋 婺城区校级期末）已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1，h2，h3，△ABC的高为h．回答以下问题：
（1）如图（1），若点P在一边BC上，此时h3＝0，可得结论　h＝h1+h2　（结论用h1，h2，h3，h的关系式表示）
（2）如图（2），当点P在△ABC内，此时可得结论　h＝h1+h2+h3　（结论用h1，h2，h3，h的关系式表示）
（3）如图（3），当点P在△ABC外，上述结论是否成立？若成立，请予以证明；若不成立，h1，h2，h3和h之间又有怎样的关系，并说明理由．
【分析】（1）连接AP，根据S△ABC＝S△ABP+S△APC可知BC AMAB PDAC PF，再把AB＝BC＝AC及AM＝h，PD＝h1，PF＝h2，代入即可得出结论；
（2）连接AP、BP、CP，根据S△ABC＝S△ABP+S△BPC+S△ACP即可得出结论；
（3）连接PB，PC，PA，由三角形的面积公式得：S△ABC＝S△PAB+S△PAC﹣S△PBC，即BC AMAB PDAC PEBC PF，再由AB＝BC＝AC即可得出结论．
【详解】解：（1）h＝h1+h2，理由如下：
连接AP，则 S△ABC＝S△ABP+S△APC
∴BC AMAB PDAC PF
即 BC hAB h1AC h2
又∵△ABC是等边三角形
∴BC＝AB＝AC，
∴h＝h1+h2．
故答案为：h＝h1+h2．
（2）h＝h1+h2+h3 ，理由如下：
连接AP、BP、CP，则 S△ABC＝S△ABP+S△BPC+S△ACP
∴BC AMAB PDAC PFBC PE
即 BC hAB h1AC h2+BC h3
又∵△ABC是等边三角形，
∴BC＝AB＝AC．
∴h＝h1+h2+h3．
故答案为：h＝h1+h2+h3；
（3）h＝h1+h2﹣h3．
当点P在△ABC外时，结论h1+h2+h3＝h不成立．此时，它们的关系是h1+h2﹣h3＝h．
理由如下：连接PB，PC，PA
由三角形的面积公式得：S△ABC＝S△PAB+S△PAC﹣S△PBC，
即BC AMAB PDAC PEBC PF，
∵AB＝BC＝AC，
∴h1+h2﹣h3＝h，
即h1+h2﹣h3＝h．
【点睛】本题考查的是等边三角形的性质，根据题意作出辅助线，构造出三角形，根据三角形的面积公式求解是解答此题的关键．