第四章 相似三角形章末复习---A+X型+旋转型相似课件（共20张PPT）

(共20张PPT)
浙教版九年级上册
第四章 相似三角形章末复习
--------A型+8字型+旋转型+飞镖型
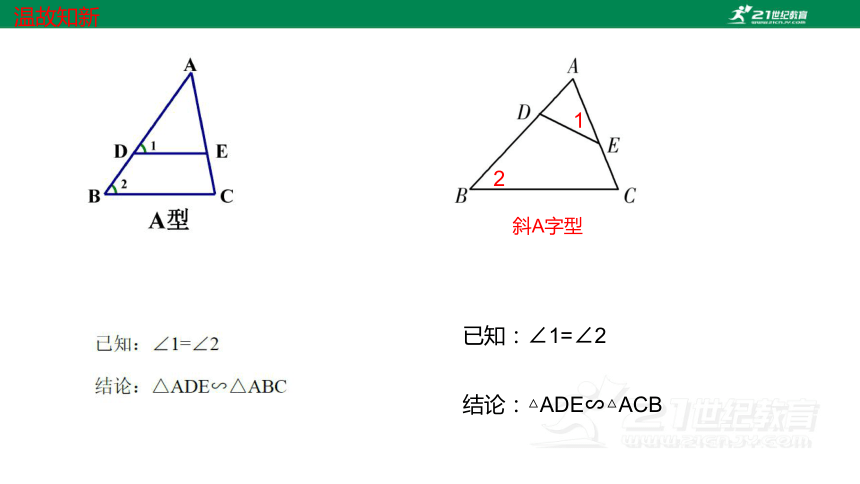
斜A字型
1
2
已知：∠1=∠2
结论：△ADE∽△ACB
温故知新
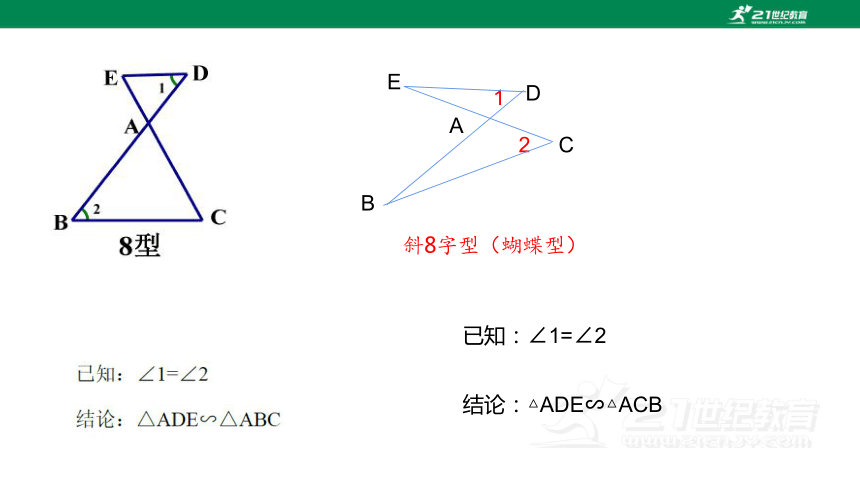
斜8字型（蝴蝶型）
已知：∠1=∠2
结论：△ADE∽△ACB
1
2
A
B
C
D
E
A
B
C
D
E
F
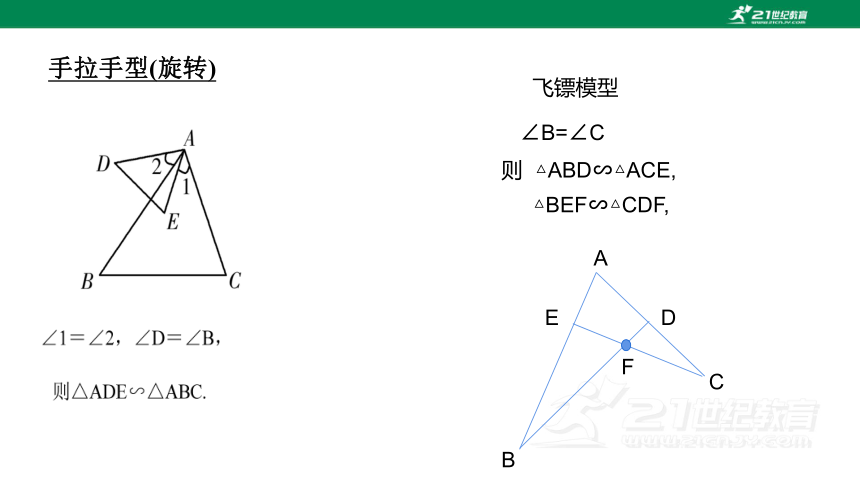
飞镖模型
∠B=∠C
则 △ABD∽△ACE,
△BEF∽△CDF,
手拉手型(旋转)
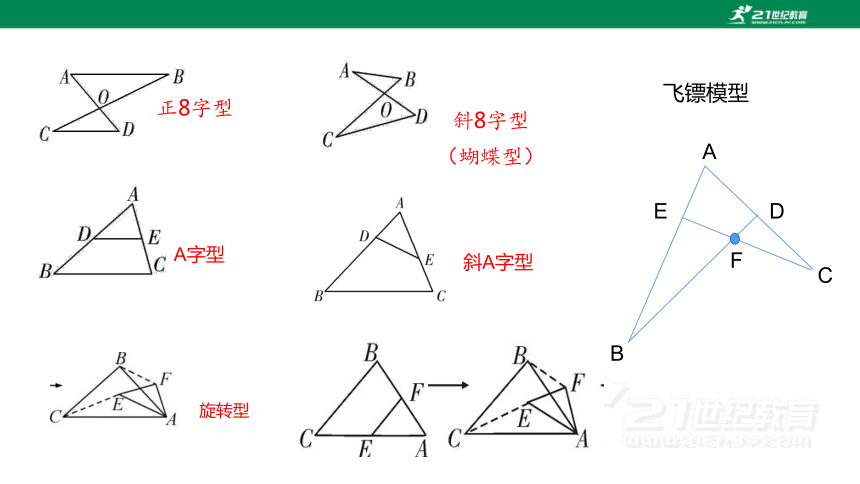
正8字型
斜8字型（蝴蝶型）
A字型
斜A字型
旋转型
A
B
C
D
E
F
飞镖模型
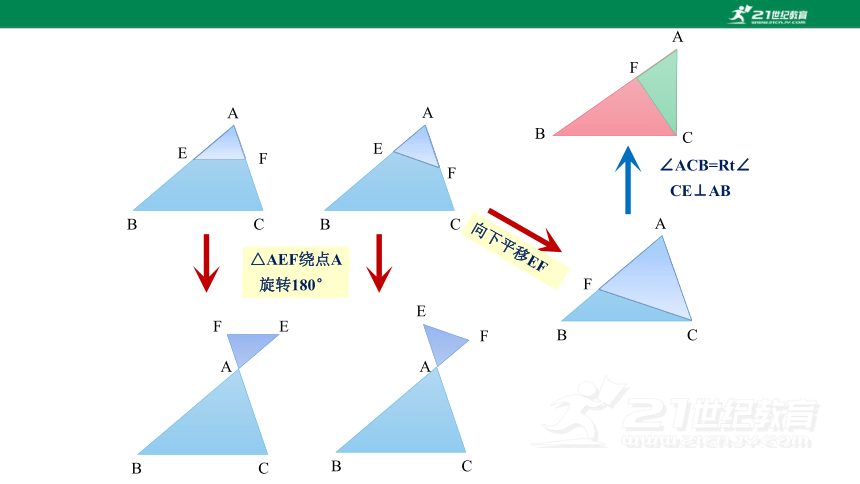
A
E
F
B
C
△AEF绕点A
旋转180°
A
E
F
B
C
A
E
F
B
C
向下平移EF
A
F
B
C
∠ACB=Rt∠
CE⊥AB
A
F
B
C
A
E
B
C
F
C
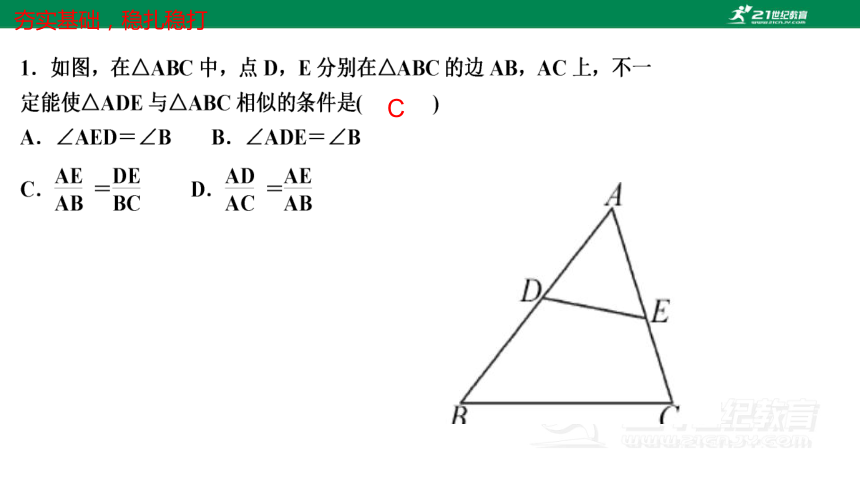
夯实基础，稳扎稳打
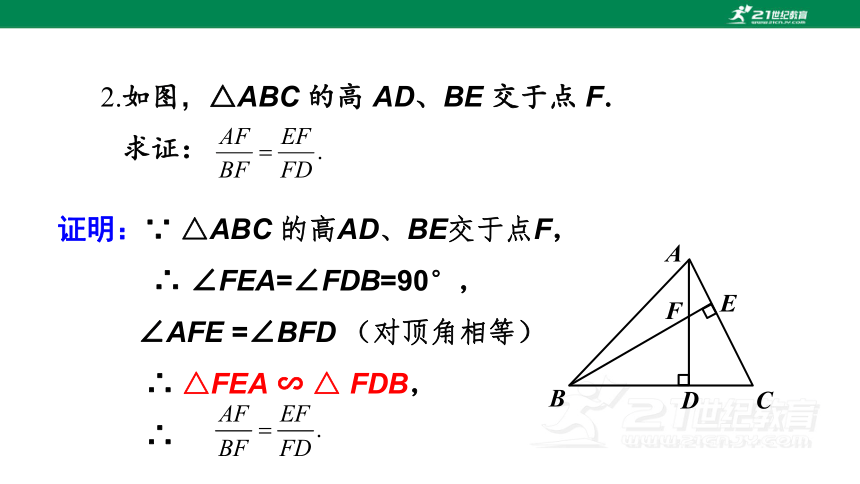
2.如图，△ABC 的高 AD、BE 交于点 F．
求证：
D
C
A
B
E
F
证明：∵ △ABC 的高AD、BE交于点F，
∴ ∠FEA=∠FDB=90°，
∠AFE =∠BFD （对顶角相等）
∴ △FEA ∽ △ FDB，
∴
图中找模型
相似得比例
比例来计算
计算求线段
5.已知：弦AB和CD相交于⊙O内一点P,
求证:
A
B
P
O
O
D
C
B
P
证明:连接AC、BD.
∵∠A、∠D都是弧CB所对的圆周角,
∴ ∠A=∠D.
同理: ∠C=∠B.
∴△PAC∽△PDB.
∴ .
04
1
2
6.已知：四边形ABDC,∠1=∠2，求证：△AOB∽△COD
证明：
∵∠1=∠2，
∴ △AOC∽△BOD
∠AOC=∠BOD
∴
.
∴
.
∵∠AOB=∠COD
∴ △AOB∽△COD
A、B、C、D四点共圆
连续递推，豁然开朗
7. 如图，CD⊥AB于D，BE⊥AC于E，
（1）求证：△ADC∽△AEB；
E
D
A
B
C
（1）证明：∵CD⊥AB，BE⊥AC，
∴∠ADC=∠AEB=90°
又∠A=∠A
∴△ADC∽△AEB
（2）连接DE，△ADE与△ABC相似吗？为什么？
（2）答△ADE与△ABC相似。
理由：由（1）知△ADC∽△AEB，
∴ ，∴ ，
又∠A=∠A， ∴△ADE∽△ACB
8. 在△ABC中,AC=4,AB=5.D是AB上一动点,且∠ADE=∠B,设AD=x,AE=y,写出y与x之间的函数关系式.
试确定x的取值范围.
( 0解: ∵∠A=∠A ∵∠ADE=∠B ∴△ADE∽△ABC ∴AD:AB=AE:AC ∴x:5=y:4 ∴y=0.8x
9:如图, 在Rt△ABC中，AC=3，BC=4，若P ， Q 分别是 BA ，BC 上的动点，
连接 PQ ， BP=CQ=m. 是否存在这样的 m ，使得 △BPQ 与△ABC相似
若存在，求出 m 的值；若不存在，请说明理由.
P
Q
m
m
Q
P
m
m
m=
.
m=
.
10.如图，已知 是半圆 的直径，弦 ， 相交于点 ，
若 ，则 的值为( )
A. B. C. D.
D
11.如图,在边长为的菱形ABCD中,∠B=30°,过点A作AE⊥BC于点E,现将△ABE沿直线AE翻折至△AFE的位置,AF与CD交于点G,则CG的长为　　　　
解:在Rt△ABE中,∠B=30°,AB=,
∴BE=.
根据折叠性质可得BF=2BE=3.
∴CF=3-.
∵AD∥CF,∴△ADG∽△FCG.
∴.设CG=x,则,解得x=-1.
.
12. 如图，O为矩形ABCD的中心，将三角尺的直角顶点与点O重合，直角边分别与矩形的两边AB，BC分别相交于点N和M，当三角尺绕点O旋转时始终与AB，BC相交.如果AB＝4，AD＝6，OM＝x，ON＝y，试写出y与x的表达式.
解：如图所示，过点 O作OE⊥AB 于点E，过点 O作OF⊥BC 于点F.
F
E
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin