浙教版八上数学压轴题--专题04 三角形压轴题考点训练(解析版)
文档属性
| 名称 | 浙教版八上数学压轴题--专题04 三角形压轴题考点训练(解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-28 16:52:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
三角形压轴题考点训练
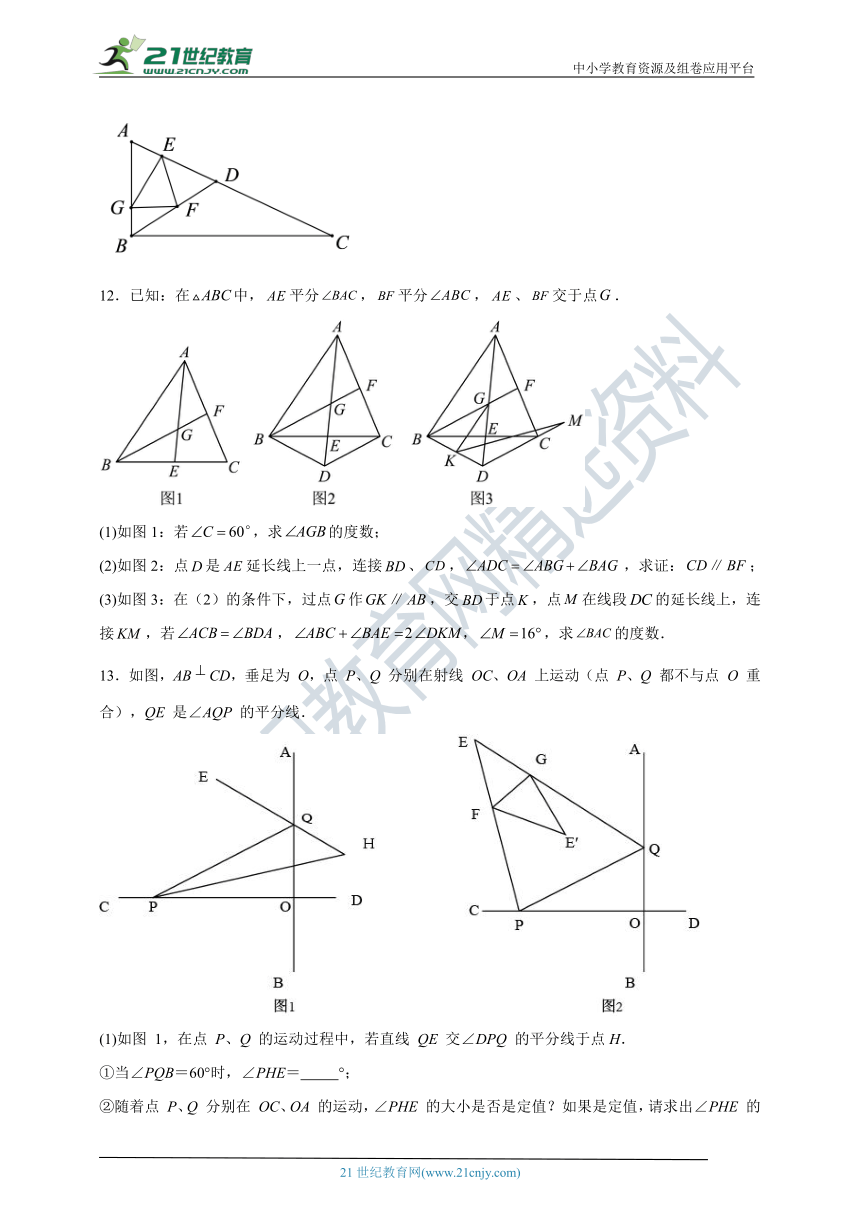
1.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第2021个三角形中以A2020为顶点的底角度数是( )
A.()2020 75° B.()2020 65°
C.()2021 75 D.()2021 65°
2.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
3.如图,在中,平分,于点.的角平分线所在直线与射线相交于点,若,且,则的度数为( )
A. B. C. D.
4.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G.若∠BEG=40°,则∠DEH的度数为( )
A.50° B.75° C.100° D.125°
5.如图,AB⊥AF,∠B、∠C、∠D、∠E、∠F的关系为( )
A.∠B+∠C+∠D+∠E+∠F=270° B.∠B+∠C﹣∠D+∠E+∠F=270°
C.∠B+∠C+∠D+∠E+∠F=360° D.∠B+∠C﹣∠D+∠E+∠F=360°
6.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3 B. C. D.6
7.如图,是的中线,点F在上,延长交于点D.若,则______.
8.如图,在中,,、分别平分、,M、N、Q分别在、、的延长线上,、分别平分、,、分别平分、,则_______.
9.如图,在中,点D,点E分别是AC和AB上的点,且满足,,过点A的直线l平行BC,射线BD交CE于点O,交直线l于点若的面积为12,则四边形AEOD的面积为____________.
10.如图,在中,,和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得,则________度.
11.如图,在中,,在边上取点,使得,连接.点、分别为、边上的点,且,将沿直线翻折,使点落在边上的点处,若,则的度数为_______.
12.已知:在中,平分,平分,、交于点.
(1)如图1:若,求的度数;
(2)如图2:点是延长线上一点,连接、,,求证:;
(3)如图3:在(2)的条件下,过点作,交于点,点在线段的延长线上,连接,若,,,求的度数.
13.如图,AB CD,垂足为 O,点 P、Q 分别在射线 OC、OA 上运动(点 P、Q 都不与点 O 重合),QE 是∠AQP 的平分线.
(1)如图 1,在点 P、Q 的运动过程中,若直线 QE 交∠DPQ 的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点 P、Q 分别在 OC、OA 的运动,∠PHE 的大小是否是定值?如果是定值,请求出∠PHE 的度数;如果不是定值,请说明理由;
(2)如图 2,若 QE 所在直线交∠QPC 的平分线于点 E 时,将△EFG 沿 FG 折叠,使点 E 落在四边形PFGQ 内点E′ 的位置,猜测∠PFE′与∠QGE′ 之间的数量关系,并说明理由.
14.阅读下列材料:
阳阳同学遇到这样一个问题:如图1,在中,是的高,是边上一点,、分别与直线,垂直,垂足分别为点、.
求证:.
阳阳发现,连接,有,即.由,可得.
他又画出了当点在的延长线上,且上面问题中其他条件不变时的图形,如图2所示,他猜想此时、、之间的数量关系是:.
请回答:
(1)请补全阳阳同学证明猜想的过程;
证明:连接.________,
________________.
,.
(2)参考阳阳同学思考问题的方法,解决下列问题:
在中,,是的高.是所在平面上一点,、、分别与直线、、垂直,垂足分别为点、、.
①如图3,若点在的内部,猜想、、、之间的数量关系并写出推理过程.
②若点在如图4所示的位置,利用图4探究得此时、、、之间的数量关系是:_______.(直接写出结论即可)
15.如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、之间存在着怎样的数量关系(用、表示),直接写出结论.
三角形压轴题考点训练
1.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第2021个三角形中以A2020为顶点的底角度数是( )
A.()2020 75° B.()2020 65°
C.()2021 75 D.()2021 65°
【答案】A
【详解】解∶∵∠B=30°,A1B=CB,∴∠BA1C=∠C,30°+∠BA1C+∠C=180°.
∴2∠BA1C=150°.∴∠BA1C=×150°=75°.
∵A1A2=A1D,∴∠DA2A1=∠A1DA2.∴∠BA1C=∠DA2A1+∠A2DA1=2∠DA2A1.
∴∠DA2A1=∠BA1C=××150°.同理可得:∠EA3A2=∠DA2A1=×××150°.…
以此类推,以An为顶点的内角度数是.
∴以A2021为顶点的内角度数是.
故选 A.
2.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
【答案】C
【详解】∵BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠ABC+∠ACB+∠1=180°,
∴∠ABC+∠ACB=180°-∠1,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠1)=90°-∠1,
∴∠BOC=180°-∠OBC-∠OCB=180°-(90°-∠1)=90°+∠1,
∵∠ACD=∠ABC+∠1,CE平分∠ACD,
∴∠ECD=∠ACD=(∠ABC+∠1),
∵∠ECD=∠OBC+∠2,
∴∠2=∠1,即∠1=2∠2,
∴∠BOC=90°+∠1=90°+∠2,
∴①④正确,②③错误,
故选C.
3.如图,在中,平分,于点.的角平分线所在直线与射线相交于点,若,且,则的度数为( )
A. B. C. D.
【答案】C
【详解】∵平分,平分
∴,
设
∵
∴可以假设,
∴
∵
∴
∴
设,则
∴
∴
∵
∴
故答案选:C
4.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G.若∠BEG=40°,则∠DEH的度数为( )
A.50° B.75° C.100° D.125°
【答案】C
【详解】解:设∠FBE=∠FEB=α,则∠AFE=2α,
∠FEH的角平分线为EG,设∠GEH=∠GEF=β,
∵AD∥BC,∴∠ABC+∠BAD=180°,
∵∠D=∠ABC,∴∠D+∠BAD=180°,∴AB∥CD,
∵∠BEG=40°,∴∠BEG=∠FEG-∠FEB=β-α=40°,
∵∠AEF=180°-∠FEG-∠HEG=180°-2β,
在△AEF中,180°-2β+2α+∠FAE=180°,∴∠FAE=2β-2α=2(β-α)=80°,
∵AB∥CD,∴∠CEH=∠FAE=80°,∴∠DEH=180°-∠CEH=100°.
故选:C.
5.如图,AB⊥AF,∠B、∠C、∠D、∠E、∠F的关系为( )
A.∠B+∠C+∠D+∠E+∠F=270° B.∠B+∠C﹣∠D+∠E+∠F=270°
C.∠B+∠C+∠D+∠E+∠F=360° D.∠B+∠C﹣∠D+∠E+∠F=360°
【答案】B
【详解】解:连接AD,
在△DMA中,∠DMA+∠MDA+∠MAD=180°,
在△DNA中,∠DNA+∠NDA+∠NAD=180°,
∴∠DMA+∠MDA+∠MAD+∠DMA+∠NDA+∠NAD=360°,
∵∠MAD+∠NAD=360°﹣∠BAF,
∴∠DMA+∠DNA+∠MDN+360°﹣∠BAF=360°,
∵AB⊥AF,
∴∠BAF=90°,
∴∠DMA+∠DNA=90°﹣∠MDN,
∵∠DMA=∠1,∠DNA=∠2,
∵∠1=180°﹣∠B﹣∠C,∠2=180°﹣∠E﹣∠F,
∴∠1+∠2=360°﹣(∠B+∠C+∠E+∠F),
∴90°﹣∠MDN=360°﹣(∠B+∠C+∠E+∠F),
∴∠B+∠C+∠E+∠F﹣∠MDN=270°.
故选:B.
6.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3 B. C. D.6
【答案】A
【详解】解:∵,
∴,
∵,,,
∴,
∴①,
同理,∵,,
∴,,∴,∴②,
由①-②得:.
故选:A.
7.如图,是的中线,点F在上,延长交于点D.若,则______.
【答案】
【详解】解:连接ED
是的中线,
,
设,
与是等高三角形,
,故答案为:.
8.如图,在中,,、分别平分、,M、N、Q分别在、、的延长线上,、分别平分、,、分别平分、,则_______.
【答案】52°
【详解】解:、分别平分、,,,
,,
即,,,
、分别平分、,,,
,
,∴,
∴,
、分别平分、,
,,
∴,
,
故答案为:52°.
9.如图,在中,点D,点E分别是AC和AB上的点,且满足,,过点A的直线l平行BC,射线BD交CE于点O,交直线l于点若的面积为12,则四边形AEOD的面积为____________.
【答案】
【详解】如图,连接AO,
∵CD=3AD,∴AD:CD=1:3,∴,,,
∵,∴,,
∵AF∥BC,∴,∴,∴,,
∵AE=2BE,∴BE:AE=1:2,∴,,
∴,,
∴,
即,
∴,即,
∴,
∵,
∴,
∴S四边形AEOD.
故答案为:.
10.如图,在中,,和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得,则________度.
【答案】
【详解】解:∵BA1平分∠ABC,A1C平分∠ACD,
∴∠A1CD=∠ACD,∠A1BC=∠ABC.
∵∠A1=∠A1CD-∠A1BC,
∴∠A1=∠ACD ABC=∠A.
同理可证:∠A2=∠A1.
∴∠A2= ∠A= ()2∠A.
以此类推,∠An=()n∠A.
当n=2022,∠A2021=()2022∠A=()2022 m°=()°.
故答案为:.
11.如图,在中,,在边上取点,使得,连接.点、分别为、边上的点,且,将沿直线翻折,使点落在边上的点处,若,则的度数为_______.
【答案】
【详解】折叠
,
设
,
,
是的一个外角,,即①
即
即②
②-①得
即
故答案为:
12.已知:在中,平分,平分,、交于点.
(1)如图1:若,求的度数;
(2)如图2:点是延长线上一点,连接、,,求证:;
(3)如图3:在(2)的条件下,过点作,交于点,点在线段的延长线上,连接,若,,,求的度数.
【答案】(1);(2)证明见解析;(3)64°
【解析】(1)证明:∵、分别平分与
∴,,
在中,,
∴
∴
∴
(2)证明:∵是得一个外角,∴,
∵,∴,∴.
(3)解: , ,
∵平分,平分,
∴设,,∴,
∵,
∴,
∵,
∴
∴,
∴
∵,,
而
∴
∴
∴
13.如图,AB CD,垂足为 O,点 P、Q 分别在射线 OC、OA 上运动(点 P、Q 都不与点 O 重合),QE 是∠AQP 的平分线.
(1)如图 1,在点 P、Q 的运动过程中,若直线 QE 交∠DPQ 的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点 P、Q 分别在 OC、OA 的运动,∠PHE 的大小是否是定值?如果是定值,请求出∠PHE 的度数;如果不是定值,请说明理由;
(2)如图 2,若 QE 所在直线交∠QPC 的平分线于点 E 时,将△EFG 沿 FG 折叠,使点 E 落在四边形PFGQ 内点E′ 的位置,猜测∠PFE′与∠QGE′ 之间的数量关系,并说明理由.
【答案】(1)①45°;②∠PHE 是一个定值,∠PHE =45°,理由见解析
(2),理由见解析
【解析】(1)解:①∵AB⊥CD,∴∠POQ=90°,∴∠PQO+∠QPO=90°,
∵∠PQB=60°,∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,∴,,
∴,故答案为:45;
②∠PHE 是一个定值,∠PHE =45°,理由如下: ∵AB⊥CD,∴∠POQ=90°,
∴∠PQO+∠QPO=90°,∴∠QPO=90°-∠PQO,∠AQP=180°-∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴;
(2)解:,理由如下:
如图所示,连接,
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°-∠CPQ+180°-∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°-∠EPQ-∠EQP=45°,
由折叠的性质可知,
∵,
∴,
∴,
∵,
∴.
14.阅读下列材料:
阳阳同学遇到这样一个问题:如图1,在中,是的高,是边上一点,、分别与直线,垂直,垂足分别为点、.
求证:.
阳阳发现,连接,有,即.由,可得.
他又画出了当点在的延长线上,且上面问题中其他条件不变时的图形,如图2所示,他猜想此时、、之间的数量关系是:.
请回答:
(1)请补全阳阳同学证明猜想的过程;
证明:连接.________,
________________.
,.
(2)参考阳阳同学思考问题的方法,解决下列问题:
在中,,是的高.是所在平面上一点,、、分别与直线、、垂直,垂足分别为点、、.
①如图3,若点在的内部,猜想、、、之间的数量关系并写出推理过程.
②若点在如图4所示的位置,利用图4探究得此时、、、之间的数量关系是:_______.(直接写出结论即可)
【答案】(1)S△APB;PN;PM;(2)①BD=PM+PN+PQ,证明见解析②BD=PM+PQ PN.
【详解】解:(1)证明:连接AP.∵S△ABC=S△APC S△APB,∴AC BD=AC PN AB PM.
∵AB=AC,∴BD=PN PM.故答案为:S△APB;PN;PM;
(2)①BD=PM+PN+PQ; 如图3,连接AP、BP、CP,
∵S△ABC=S△APC+S△APB+S△BPC,∴AC BD=AC PN+AB PM+BC PQ,
∵AB=AC=BC,∴BD=PM+PN+PQ;
②BD=PM+PQ PN;如图4,连接AP、BP、CP,∵S△ABC=S△APB+S△BPC S△APC.
∴AC BD=AB PM+BC PQ AC PN,
∵AB=AC=BC,∴BD=PM+PQ PN.
15.如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、之间存在着怎样的数量关系(用、表示),直接写出结论.
【答案】(1)33°;(2) .
【详解】解:(1)∵AP是∠DAB的角平分线,CP是∠DCB的角平分线
∴∠DAP=PAB,∠DCP=∠PCB
∵∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP
∴∠P+∠PAB+∠P+∠PCD=∠B+∠PCB+∠D+∠DAP
∴2∠P=∠B+∠D
∵∠B=28°,∠D=38°
∴∠P=33°
(2) ∠P=
∵∠P+∠PCD=∠D+∠DAP
∴∠PCD-∠DAP=∠D-∠P
∵∠D+∠DAO=∠B+∠OCB
∴∠DAB-∠DCB=∠B-∠D
∵,
∴∠DAB-∠DCB=3(∠DAP-∠DCP)
∴∠B-∠D=3(∠P-∠D)
∵,
∴∠P=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
三角形压轴题考点训练
1.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第2021个三角形中以A2020为顶点的底角度数是( )
A.()2020 75° B.()2020 65°
C.()2021 75 D.()2021 65°
2.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
3.如图,在中,平分,于点.的角平分线所在直线与射线相交于点,若,且,则的度数为( )
A. B. C. D.
4.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G.若∠BEG=40°,则∠DEH的度数为( )
A.50° B.75° C.100° D.125°
5.如图,AB⊥AF,∠B、∠C、∠D、∠E、∠F的关系为( )
A.∠B+∠C+∠D+∠E+∠F=270° B.∠B+∠C﹣∠D+∠E+∠F=270°
C.∠B+∠C+∠D+∠E+∠F=360° D.∠B+∠C﹣∠D+∠E+∠F=360°
6.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3 B. C. D.6
7.如图,是的中线,点F在上,延长交于点D.若,则______.
8.如图,在中,,、分别平分、,M、N、Q分别在、、的延长线上,、分别平分、,、分别平分、,则_______.
9.如图,在中,点D,点E分别是AC和AB上的点,且满足,,过点A的直线l平行BC,射线BD交CE于点O,交直线l于点若的面积为12,则四边形AEOD的面积为____________.
10.如图,在中,,和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得,则________度.
11.如图,在中,,在边上取点,使得,连接.点、分别为、边上的点,且,将沿直线翻折,使点落在边上的点处,若,则的度数为_______.
12.已知:在中,平分,平分,、交于点.
(1)如图1:若,求的度数;
(2)如图2:点是延长线上一点,连接、,,求证:;
(3)如图3:在(2)的条件下,过点作,交于点,点在线段的延长线上,连接,若,,,求的度数.
13.如图,AB CD,垂足为 O,点 P、Q 分别在射线 OC、OA 上运动(点 P、Q 都不与点 O 重合),QE 是∠AQP 的平分线.
(1)如图 1,在点 P、Q 的运动过程中,若直线 QE 交∠DPQ 的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点 P、Q 分别在 OC、OA 的运动,∠PHE 的大小是否是定值?如果是定值,请求出∠PHE 的度数;如果不是定值,请说明理由;
(2)如图 2,若 QE 所在直线交∠QPC 的平分线于点 E 时,将△EFG 沿 FG 折叠,使点 E 落在四边形PFGQ 内点E′ 的位置,猜测∠PFE′与∠QGE′ 之间的数量关系,并说明理由.
14.阅读下列材料:
阳阳同学遇到这样一个问题:如图1,在中,是的高,是边上一点,、分别与直线,垂直,垂足分别为点、.
求证:.
阳阳发现,连接,有,即.由,可得.
他又画出了当点在的延长线上,且上面问题中其他条件不变时的图形,如图2所示,他猜想此时、、之间的数量关系是:.
请回答:
(1)请补全阳阳同学证明猜想的过程;
证明:连接.________,
________________.
,.
(2)参考阳阳同学思考问题的方法,解决下列问题:
在中,,是的高.是所在平面上一点,、、分别与直线、、垂直,垂足分别为点、、.
①如图3,若点在的内部,猜想、、、之间的数量关系并写出推理过程.
②若点在如图4所示的位置,利用图4探究得此时、、、之间的数量关系是:_______.(直接写出结论即可)
15.如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、之间存在着怎样的数量关系(用、表示),直接写出结论.
三角形压轴题考点训练
1.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第2021个三角形中以A2020为顶点的底角度数是( )
A.()2020 75° B.()2020 65°
C.()2021 75 D.()2021 65°
【答案】A
【详解】解∶∵∠B=30°,A1B=CB,∴∠BA1C=∠C,30°+∠BA1C+∠C=180°.
∴2∠BA1C=150°.∴∠BA1C=×150°=75°.
∵A1A2=A1D,∴∠DA2A1=∠A1DA2.∴∠BA1C=∠DA2A1+∠A2DA1=2∠DA2A1.
∴∠DA2A1=∠BA1C=××150°.同理可得:∠EA3A2=∠DA2A1=×××150°.…
以此类推,以An为顶点的内角度数是.
∴以A2021为顶点的内角度数是.
故选 A.
2.如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC=3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是( )
A.①②③ B.①③④ C.①④ D.①②④
【答案】C
【详解】∵BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠ABC+∠ACB+∠1=180°,
∴∠ABC+∠ACB=180°-∠1,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠1)=90°-∠1,
∴∠BOC=180°-∠OBC-∠OCB=180°-(90°-∠1)=90°+∠1,
∵∠ACD=∠ABC+∠1,CE平分∠ACD,
∴∠ECD=∠ACD=(∠ABC+∠1),
∵∠ECD=∠OBC+∠2,
∴∠2=∠1,即∠1=2∠2,
∴∠BOC=90°+∠1=90°+∠2,
∴①④正确,②③错误,
故选C.
3.如图,在中,平分,于点.的角平分线所在直线与射线相交于点,若,且,则的度数为( )
A. B. C. D.
【答案】C
【详解】∵平分,平分
∴,
设
∵
∴可以假设,
∴
∵
∴
∴
设,则
∴
∴
∵
∴
故答案选:C
4.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G.若∠BEG=40°,则∠DEH的度数为( )
A.50° B.75° C.100° D.125°
【答案】C
【详解】解:设∠FBE=∠FEB=α,则∠AFE=2α,
∠FEH的角平分线为EG,设∠GEH=∠GEF=β,
∵AD∥BC,∴∠ABC+∠BAD=180°,
∵∠D=∠ABC,∴∠D+∠BAD=180°,∴AB∥CD,
∵∠BEG=40°,∴∠BEG=∠FEG-∠FEB=β-α=40°,
∵∠AEF=180°-∠FEG-∠HEG=180°-2β,
在△AEF中,180°-2β+2α+∠FAE=180°,∴∠FAE=2β-2α=2(β-α)=80°,
∵AB∥CD,∴∠CEH=∠FAE=80°,∴∠DEH=180°-∠CEH=100°.
故选:C.
5.如图,AB⊥AF,∠B、∠C、∠D、∠E、∠F的关系为( )
A.∠B+∠C+∠D+∠E+∠F=270° B.∠B+∠C﹣∠D+∠E+∠F=270°
C.∠B+∠C+∠D+∠E+∠F=360° D.∠B+∠C﹣∠D+∠E+∠F=360°
【答案】B
【详解】解:连接AD,
在△DMA中,∠DMA+∠MDA+∠MAD=180°,
在△DNA中,∠DNA+∠NDA+∠NAD=180°,
∴∠DMA+∠MDA+∠MAD+∠DMA+∠NDA+∠NAD=360°,
∵∠MAD+∠NAD=360°﹣∠BAF,
∴∠DMA+∠DNA+∠MDN+360°﹣∠BAF=360°,
∵AB⊥AF,
∴∠BAF=90°,
∴∠DMA+∠DNA=90°﹣∠MDN,
∵∠DMA=∠1,∠DNA=∠2,
∵∠1=180°﹣∠B﹣∠C,∠2=180°﹣∠E﹣∠F,
∴∠1+∠2=360°﹣(∠B+∠C+∠E+∠F),
∴90°﹣∠MDN=360°﹣(∠B+∠C+∠E+∠F),
∴∠B+∠C+∠E+∠F﹣∠MDN=270°.
故选:B.
6.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3 B. C. D.6
【答案】A
【详解】解:∵,
∴,
∵,,,
∴,
∴①,
同理,∵,,
∴,,∴,∴②,
由①-②得:.
故选:A.
7.如图,是的中线,点F在上,延长交于点D.若,则______.
【答案】
【详解】解:连接ED
是的中线,
,
设,
与是等高三角形,
,故答案为:.
8.如图,在中,,、分别平分、,M、N、Q分别在、、的延长线上,、分别平分、,、分别平分、,则_______.
【答案】52°
【详解】解:、分别平分、,,,
,,
即,,,
、分别平分、,,,
,
,∴,
∴,
、分别平分、,
,,
∴,
,
故答案为:52°.
9.如图,在中,点D,点E分别是AC和AB上的点,且满足,,过点A的直线l平行BC,射线BD交CE于点O,交直线l于点若的面积为12,则四边形AEOD的面积为____________.
【答案】
【详解】如图,连接AO,
∵CD=3AD,∴AD:CD=1:3,∴,,,
∵,∴,,
∵AF∥BC,∴,∴,∴,,
∵AE=2BE,∴BE:AE=1:2,∴,,
∴,,
∴,
即,
∴,即,
∴,
∵,
∴,
∴S四边形AEOD.
故答案为:.
10.如图,在中,,和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得和的平分线交于点,得,则________度.
【答案】
【详解】解:∵BA1平分∠ABC,A1C平分∠ACD,
∴∠A1CD=∠ACD,∠A1BC=∠ABC.
∵∠A1=∠A1CD-∠A1BC,
∴∠A1=∠ACD ABC=∠A.
同理可证:∠A2=∠A1.
∴∠A2= ∠A= ()2∠A.
以此类推,∠An=()n∠A.
当n=2022,∠A2021=()2022∠A=()2022 m°=()°.
故答案为:.
11.如图,在中,,在边上取点,使得,连接.点、分别为、边上的点,且,将沿直线翻折,使点落在边上的点处,若,则的度数为_______.
【答案】
【详解】折叠
,
设
,
,
是的一个外角,,即①
即
即②
②-①得
即
故答案为:
12.已知:在中,平分,平分,、交于点.
(1)如图1:若,求的度数;
(2)如图2:点是延长线上一点,连接、,,求证:;
(3)如图3:在(2)的条件下,过点作,交于点,点在线段的延长线上,连接,若,,,求的度数.
【答案】(1);(2)证明见解析;(3)64°
【解析】(1)证明:∵、分别平分与
∴,,
在中,,
∴
∴
∴
(2)证明:∵是得一个外角,∴,
∵,∴,∴.
(3)解: , ,
∵平分,平分,
∴设,,∴,
∵,
∴,
∵,
∴
∴,
∴
∵,,
而
∴
∴
∴
13.如图,AB CD,垂足为 O,点 P、Q 分别在射线 OC、OA 上运动(点 P、Q 都不与点 O 重合),QE 是∠AQP 的平分线.
(1)如图 1,在点 P、Q 的运动过程中,若直线 QE 交∠DPQ 的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点 P、Q 分别在 OC、OA 的运动,∠PHE 的大小是否是定值?如果是定值,请求出∠PHE 的度数;如果不是定值,请说明理由;
(2)如图 2,若 QE 所在直线交∠QPC 的平分线于点 E 时,将△EFG 沿 FG 折叠,使点 E 落在四边形PFGQ 内点E′ 的位置,猜测∠PFE′与∠QGE′ 之间的数量关系,并说明理由.
【答案】(1)①45°;②∠PHE 是一个定值,∠PHE =45°,理由见解析
(2),理由见解析
【解析】(1)解:①∵AB⊥CD,∴∠POQ=90°,∴∠PQO+∠QPO=90°,
∵∠PQB=60°,∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,∴,,
∴,故答案为:45;
②∠PHE 是一个定值,∠PHE =45°,理由如下: ∵AB⊥CD,∴∠POQ=90°,
∴∠PQO+∠QPO=90°,∴∠QPO=90°-∠PQO,∠AQP=180°-∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴;
(2)解:,理由如下:
如图所示,连接,
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°-∠CPQ+180°-∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°-∠EPQ-∠EQP=45°,
由折叠的性质可知,
∵,
∴,
∴,
∵,
∴.
14.阅读下列材料:
阳阳同学遇到这样一个问题:如图1,在中,是的高,是边上一点,、分别与直线,垂直,垂足分别为点、.
求证:.
阳阳发现,连接,有,即.由,可得.
他又画出了当点在的延长线上,且上面问题中其他条件不变时的图形,如图2所示,他猜想此时、、之间的数量关系是:.
请回答:
(1)请补全阳阳同学证明猜想的过程;
证明:连接.________,
________________.
,.
(2)参考阳阳同学思考问题的方法,解决下列问题:
在中,,是的高.是所在平面上一点,、、分别与直线、、垂直,垂足分别为点、、.
①如图3,若点在的内部,猜想、、、之间的数量关系并写出推理过程.
②若点在如图4所示的位置,利用图4探究得此时、、、之间的数量关系是:_______.(直接写出结论即可)
【答案】(1)S△APB;PN;PM;(2)①BD=PM+PN+PQ,证明见解析②BD=PM+PQ PN.
【详解】解:(1)证明:连接AP.∵S△ABC=S△APC S△APB,∴AC BD=AC PN AB PM.
∵AB=AC,∴BD=PN PM.故答案为:S△APB;PN;PM;
(2)①BD=PM+PN+PQ; 如图3,连接AP、BP、CP,
∵S△ABC=S△APC+S△APB+S△BPC,∴AC BD=AC PN+AB PM+BC PQ,
∵AB=AC=BC,∴BD=PM+PN+PQ;
②BD=PM+PQ PN;如图4,连接AP、BP、CP,∵S△ABC=S△APB+S△BPC S△APC.
∴AC BD=AB PM+BC PQ AC PN,
∵AB=AC=BC,∴BD=PM+PQ PN.
15.如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、之间存在着怎样的数量关系(用、表示),直接写出结论.
【答案】(1)33°;(2) .
【详解】解:(1)∵AP是∠DAB的角平分线,CP是∠DCB的角平分线
∴∠DAP=PAB,∠DCP=∠PCB
∵∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP
∴∠P+∠PAB+∠P+∠PCD=∠B+∠PCB+∠D+∠DAP
∴2∠P=∠B+∠D
∵∠B=28°,∠D=38°
∴∠P=33°
(2) ∠P=
∵∠P+∠PCD=∠D+∠DAP
∴∠PCD-∠DAP=∠D-∠P
∵∠D+∠DAO=∠B+∠OCB
∴∠DAB-∠DCB=∠B-∠D
∵,
∴∠DAB-∠DCB=3(∠DAP-∠DCP)
∴∠B-∠D=3(∠P-∠D)
∵,
∴∠P=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
