第三章 圆的基本性质----定点定长存隐圆课件(共16张PPT)
文档属性
| 名称 | 第三章 圆的基本性质----定点定长存隐圆课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-29 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
浙教版九年级上册
第三章 圆的基本性质章末复习
-----------定点定长
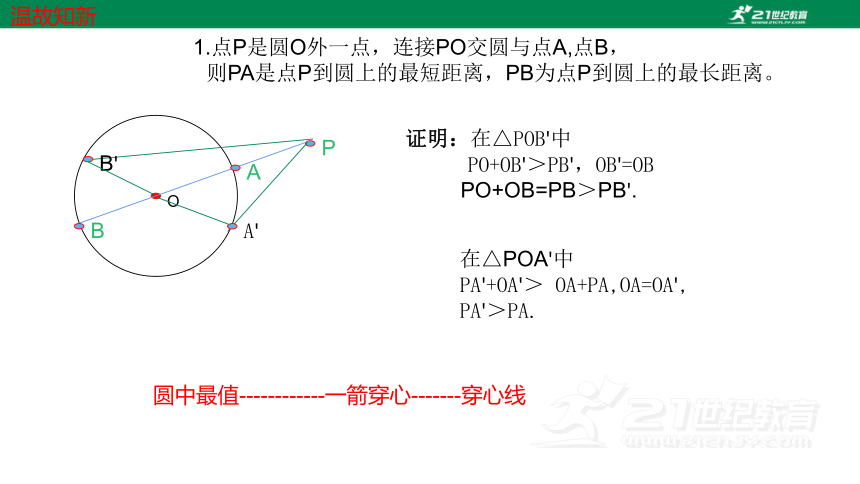
证明:在△POB'中
PO+OB'>PB',OB'=OB
PO+OB=PB>PB'.
在△POA'中
PA'+OA'> OA+PA,OA=OA',
PA'>PA.
1.点P是圆O外一点,连接PO交圆与点A,点B,
则PA是点P到圆上的最短距离,PB为点P到圆上的最长距离。
圆中最值------------一箭穿心-------穿心线
O
P
A
B
B'
A'
温故知新
2.点P是圆O内一点,连接PO交圆与点A,点B,则PA是点P到圆上
的最短距离,PB为点P到圆上的最长距离。
O
P
A
B
A'
B'
证明:在△POB'中
PO+OB'>PB',OB'=OB
PO+OB=PB>PB'.
在△POA'中
PA'+OP> OA'=PA+OP,
PA'>PA.
圆中最值------------一箭穿心-------穿心线
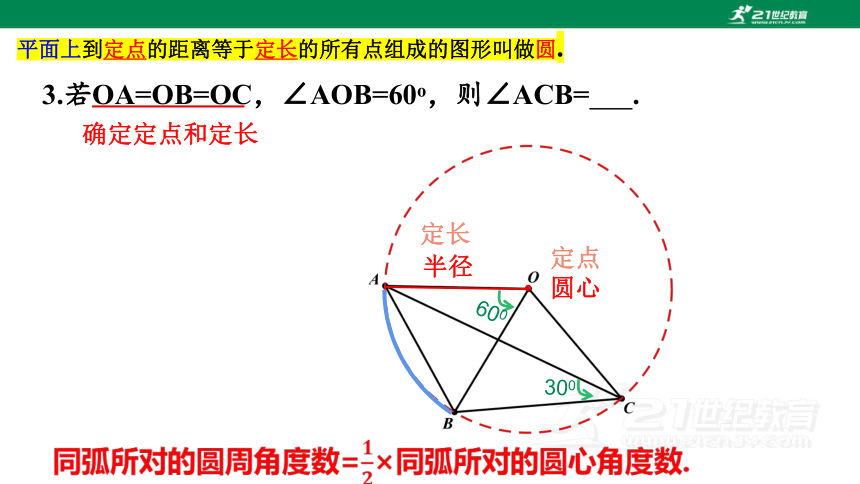
3.若OA=OB=OC,∠AOB=60o,则∠ACB= .
确定定点和定长
圆心
定点
定长
半径
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
600
300
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
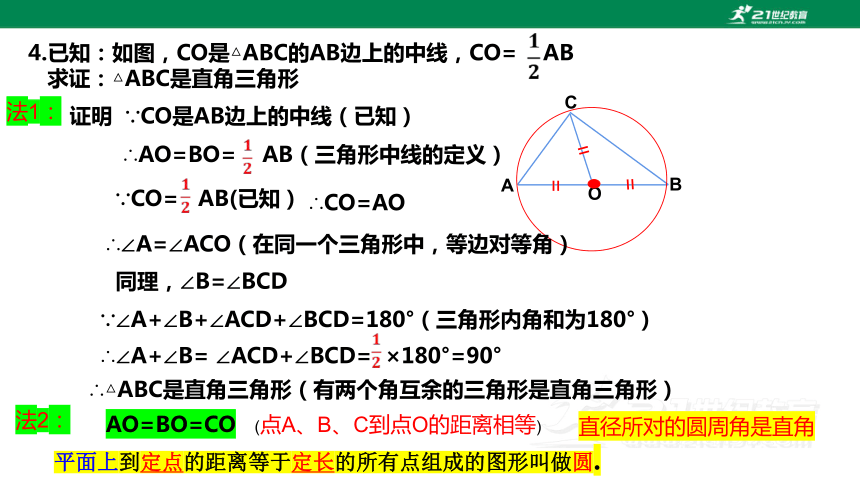
4.已知:如图,CO是△ABC的AB边上的中线,CO= AB
求证:△ABC是直角三角形
C
A
O
B
=
=
=
证明 ∵CO是AB边上的中线(已知)
∴AO=BO= AB(三角形中线的定义)
∵CO= AB(已知)
(点A、B、C到点O的距离相等)
∴CO=AO
∴∠A=∠ACO(在同一个三角形中,等边对等角)
同理,∠B=∠BCD
∵∠A+∠B+∠ACD+∠BCD=180°(三角形内角和为180°)
∴∠A+∠B= ∠ACD+∠BCD= ×180°=90°
∴△ABC是直角三角形(有两个角互余的三角形是直角三角形)
法1:
法2:
AO=BO=CO
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
直径所对的圆周角是直角
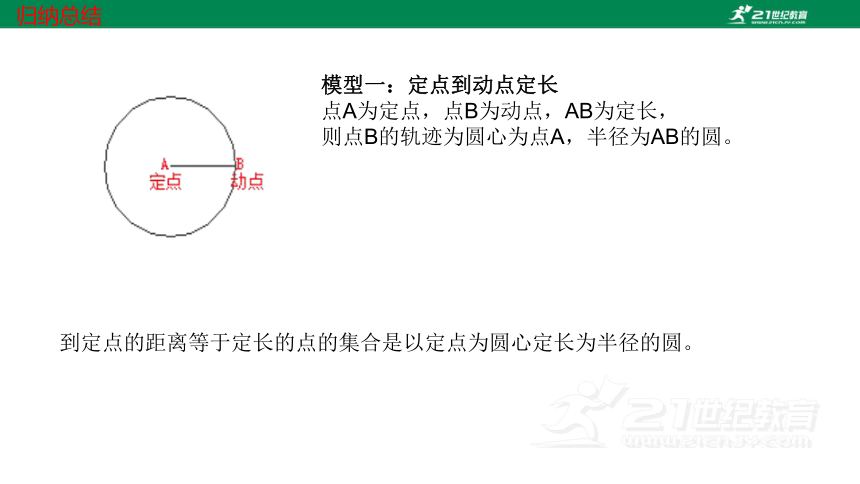
到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆。
模型一:定点到动点定长
点A为定点,点B为动点,AB为定长,
则点B的轨迹为圆心为点A,半径为AB的圆。
归纳总结
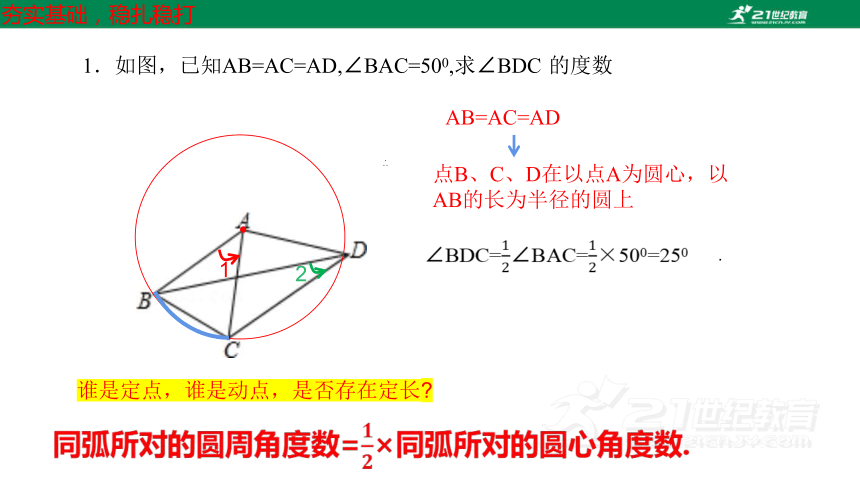
1.如图,已知AB=AC=AD,∠BAC=500,求∠BDC 的度数
AB=AC=AD
点B、C、D在以点A为圆心,以
AB的长为半径的圆上
∠BDC=∠BAC=×500=250
.
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
1
2
夯实基础,稳扎稳打
谁是定点,谁是动点,是否存在定长
2.如图,木杆AB=2,靠在墙壁上,当木杆的上端A沿墙壁竖直下滑时,木杆的底端B 也沿着水平方向向右滑动.你能用虚线画出木杆中点M 随之运动的轨迹吗?
OM=1
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
点M在以O为圆心,
1为半径的 圆上
.
谁是定点,谁是动点,是否存在定长
3.木杆AB=2,以AB为作等边△ABC,如图所示, 连接OC,
当木杆AB在下滑过程中,试求OC的最大值.
OM+MC≥OC
1+
OC≤1+
4.如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,
求∠ADC的度数.
圆内接四边形对角互补
E
解:∵AB=BD=BC,
∴A、D、C在以B为圆心,以AB为半径的圆上,
如图,作圆周角∠AEC,
∵∠ABC=112°,
∴∠E=∠ABC=56°,
∵四边形ADCE是⊙B的圆内接四边形,
∴∠ADC+∠E=180°,
∴∠ADC=180°﹣56°=124°,
.
谁是定点,谁是动点,是否存在定长
5.如图,四边形ABCD中,AE、AF分别是BC,CD的中垂线,∠EAF=800,∠C BD=300, 求∠ABC的度数
B,C,D在以A为圆心,AB为半径的圆上
AB=AC=AD
∠DAC=2∠DBC=2×300=600
.
∠DAF=∠CAF=300
.
300
600
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
连续递推,豁然开朗
6.如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点M,求线段MC的最小值
M在以A圆心,3为半径的圆上
当A,M,C三点共线时,CM最短
AB=AM=3
M
谁是定点,谁是动点,是否存在定长
7.如图,点A,B的坐标分别为A(3,0)、A'( -3, 0) 、B(0,3),点C为坐标平面内的一点,且BC=2,点M为线段AC的中点,连接OM,求OM的最大值
∴当A'C最大时,OM最大,
∵点C为坐标平面内的一点,且BC=2,
∴点C在以B为圆心,2为半径的⊙B上运动,
∴当A'C经过圆心B时,A′C最大,即点C在图中C'位置.A'C'=AB+BC'=3
∴OM的最大值 +1
.
A'
解:∵点O是AA'的中点,
点M是AC的中点,
∴OM是△AA'C的中位线,
∴OM=
.
BC=2
点C在以B为圆心,
BC为半径的 圆上
C
谁是定点,谁是动点,是否存在定长
8.如图,在矩形ABCD中,AB=6,BC=8,点E为平面内一动点,且DE=2,连接BE,点M为BE的中点,求AM的最小值。
【解答】解:由题意知:E点在以D为圆心,以2为半径的圆上,连接BD,取BD的中点O,连接AO,MO,
在矩形ABCD中,∠BAD=90°,AB=8,BC=6,∴BD= =10
∵O为BD的中点,∴AO=5
∵M为BE的中点,DE=2,∴OM=1,
∵AM≥AO﹣OM,即AM≥4,∴当A,O,M三点共线时,AM有最小值为4,
思维拓展,更上一层
谁是定点,谁是动点,是否存在定长
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
第三章 圆的基本性质章末复习
-----------定点定长
证明:在△POB'中
PO+OB'>PB',OB'=OB
PO+OB=PB>PB'.
在△POA'中
PA'+OA'> OA+PA,OA=OA',
PA'>PA.
1.点P是圆O外一点,连接PO交圆与点A,点B,
则PA是点P到圆上的最短距离,PB为点P到圆上的最长距离。
圆中最值------------一箭穿心-------穿心线
O
P
A
B
B'
A'
温故知新
2.点P是圆O内一点,连接PO交圆与点A,点B,则PA是点P到圆上
的最短距离,PB为点P到圆上的最长距离。
O
P
A
B
A'
B'
证明:在△POB'中
PO+OB'>PB',OB'=OB
PO+OB=PB>PB'.
在△POA'中
PA'+OP> OA'=PA+OP,
PA'>PA.
圆中最值------------一箭穿心-------穿心线
3.若OA=OB=OC,∠AOB=60o,则∠ACB= .
确定定点和定长
圆心
定点
定长
半径
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
600
300
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
4.已知:如图,CO是△ABC的AB边上的中线,CO= AB
求证:△ABC是直角三角形
C
A
O
B
=
=
=
证明 ∵CO是AB边上的中线(已知)
∴AO=BO= AB(三角形中线的定义)
∵CO= AB(已知)
(点A、B、C到点O的距离相等)
∴CO=AO
∴∠A=∠ACO(在同一个三角形中,等边对等角)
同理,∠B=∠BCD
∵∠A+∠B+∠ACD+∠BCD=180°(三角形内角和为180°)
∴∠A+∠B= ∠ACD+∠BCD= ×180°=90°
∴△ABC是直角三角形(有两个角互余的三角形是直角三角形)
法1:
法2:
AO=BO=CO
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
直径所对的圆周角是直角
到定点的距离等于定长的点的集合是以定点为圆心定长为半径的圆。
模型一:定点到动点定长
点A为定点,点B为动点,AB为定长,
则点B的轨迹为圆心为点A,半径为AB的圆。
归纳总结
1.如图,已知AB=AC=AD,∠BAC=500,求∠BDC 的度数
AB=AC=AD
点B、C、D在以点A为圆心,以
AB的长为半径的圆上
∠BDC=∠BAC=×500=250
.
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
1
2
夯实基础,稳扎稳打
谁是定点,谁是动点,是否存在定长
2.如图,木杆AB=2,靠在墙壁上,当木杆的上端A沿墙壁竖直下滑时,木杆的底端B 也沿着水平方向向右滑动.你能用虚线画出木杆中点M 随之运动的轨迹吗?
OM=1
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
点M在以O为圆心,
1为半径的 圆上
.
谁是定点,谁是动点,是否存在定长
3.木杆AB=2,以AB为作等边△ABC,如图所示, 连接OC,
当木杆AB在下滑过程中,试求OC的最大值.
OM+MC≥OC
1+
OC≤1+
4.如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,
求∠ADC的度数.
圆内接四边形对角互补
E
解:∵AB=BD=BC,
∴A、D、C在以B为圆心,以AB为半径的圆上,
如图,作圆周角∠AEC,
∵∠ABC=112°,
∴∠E=∠ABC=56°,
∵四边形ADCE是⊙B的圆内接四边形,
∴∠ADC+∠E=180°,
∴∠ADC=180°﹣56°=124°,
.
谁是定点,谁是动点,是否存在定长
5.如图,四边形ABCD中,AE、AF分别是BC,CD的中垂线,∠EAF=800,∠C BD=300, 求∠ABC的度数
B,C,D在以A为圆心,AB为半径的圆上
AB=AC=AD
∠DAC=2∠DBC=2×300=600
.
∠DAF=∠CAF=300
.
300
600
同弧所对的圆周角度数=×同弧所对的圆心角度数.
.
连续递推,豁然开朗
6.如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点M,求线段MC的最小值
M在以A圆心,3为半径的圆上
当A,M,C三点共线时,CM最短
AB=AM=3
M
谁是定点,谁是动点,是否存在定长
7.如图,点A,B的坐标分别为A(3,0)、A'( -3, 0) 、B(0,3),点C为坐标平面内的一点,且BC=2,点M为线段AC的中点,连接OM,求OM的最大值
∴当A'C最大时,OM最大,
∵点C为坐标平面内的一点,且BC=2,
∴点C在以B为圆心,2为半径的⊙B上运动,
∴当A'C经过圆心B时,A′C最大,即点C在图中C'位置.A'C'=AB+BC'=3
∴OM的最大值 +1
.
A'
解:∵点O是AA'的中点,
点M是AC的中点,
∴OM是△AA'C的中位线,
∴OM=
.
BC=2
点C在以B为圆心,
BC为半径的 圆上
C
谁是定点,谁是动点,是否存在定长
8.如图,在矩形ABCD中,AB=6,BC=8,点E为平面内一动点,且DE=2,连接BE,点M为BE的中点,求AM的最小值。
【解答】解:由题意知:E点在以D为圆心,以2为半径的圆上,连接BD,取BD的中点O,连接AO,MO,
在矩形ABCD中,∠BAD=90°,AB=8,BC=6,∴BD= =10
∵O为BD的中点,∴AO=5
∵M为BE的中点,DE=2,∴OM=1,
∵AM≥AO﹣OM,即AM≥4,∴当A,O,M三点共线时,AM有最小值为4,
思维拓展,更上一层
谁是定点,谁是动点,是否存在定长
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
