二次函数的图象和性质
图片预览


文档简介
(共13张PPT)
二次函数的图象和性质(复习)
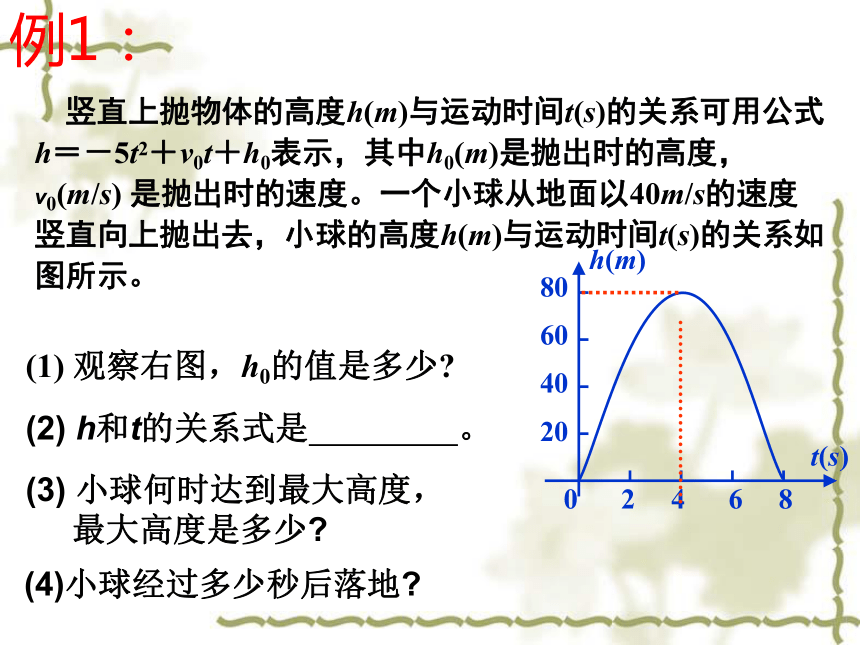
(1) 观察右图,h0的值是多少
竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式 h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s) 是抛出时的速度。一个小球从地面以40m/s的速度竖直向上抛出去,小球的高度h(m)与运动时间t(s)的关系如图所示。
(3) 小球何时达到最大高度,
最大高度是多少
0 2 4 6 8
80
60
40
20
t(s)
h(m)
(2) h和t的关系式是 。
(4)小球经过多少秒后落地
例1:
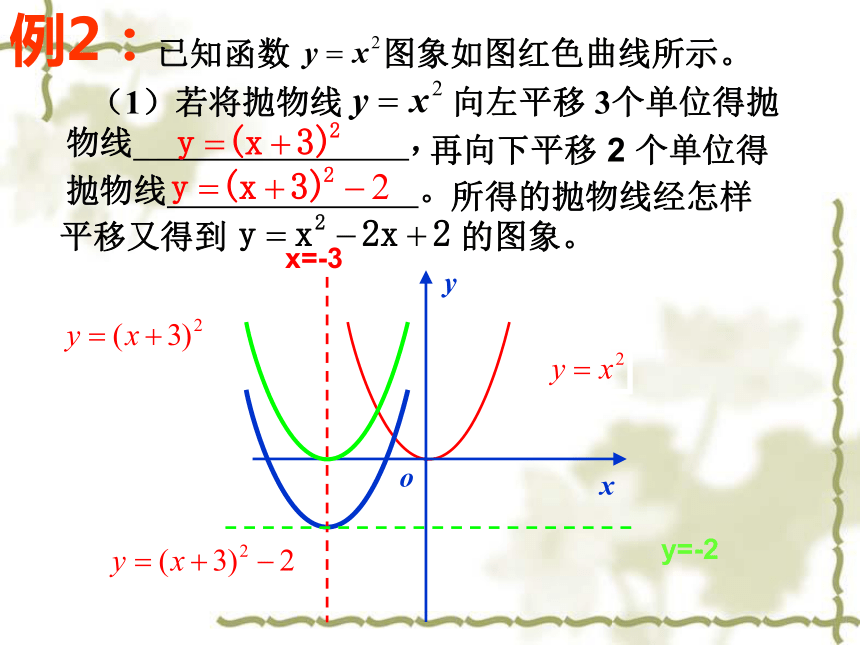
例2:
已知函数 图象如图红色曲线所示。
x
y
o
y=-2
x=-3
(1)若将抛物线 向左平移 3个单位得抛物线 ,
所得的抛物线经怎样平移又得到 的图象。
再向下平移 2 个单位得
抛物线 。
若将抛物线 沿 x 轴向左或向右平移后经过点(3,10),则平移后抛物线的解析式是 。(学生练习)
(2)将抛物线 沿 y 轴向上或向下平移后经过点(3,4),则平移后抛物线的解析式是 ;
x
y
o
(3,5)
Y=5
Y=4
Y=1
x=3
x=1
Y=x2-2x+2
(3,4)
Y=x2-2x+1
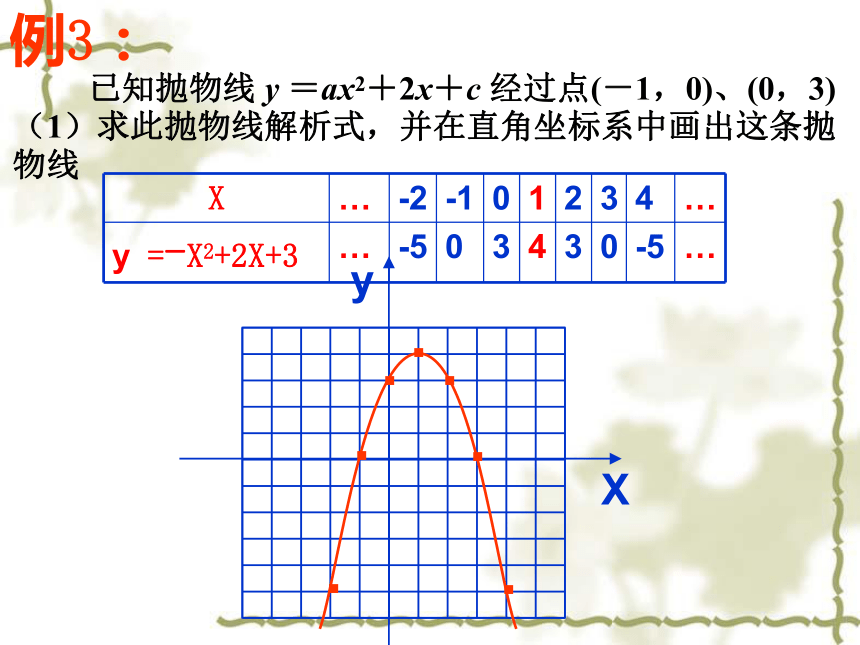
已知抛物线 y =ax2+2x+c 经过点(-1,0)、(0,3)
(1)求此抛物线解析式,并在直角坐标系中画出这条抛物线
例3:
·
·
·
·
·
X
y
·
·
X … -2 -1 0 1 2 3 4 …
y =-X2+2X+3 … -5 0 3 4 3 0 -5 …
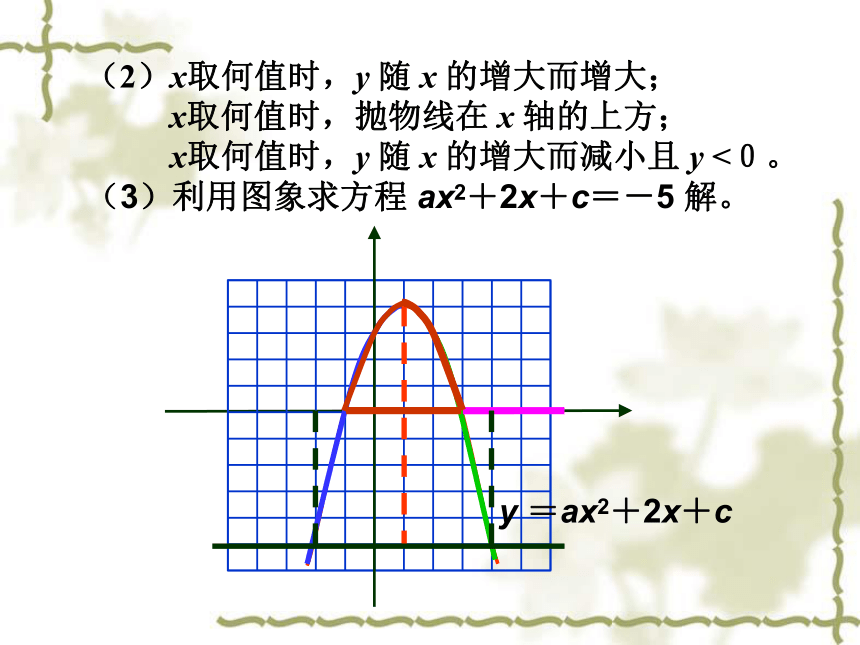
(2)x取何值时,y 随 x 的增大而增大;
x取何值时,抛物线在 x 轴的上方;
x取何值时,y 随 x 的增大而减小且 y <0。
y =ax2+2x+c
(3)利用图象求方程 ax2+2x+c=-5 解。
(4)若将上题的-5 改为2x-1, 又如何利用图象求方程ax2+2x+c=2x-1的解呢?并比较ax2+2x+c与2x-1的大小。
y =ax2+2x+c
y =2x--1
y1
y2
x
y
·
·
·
·
(5)判断方程 的解的个数。
·
·
·
·
·
·
·
答案:3个
(6)已知函数y =x3 的图象,求方程x3-x-2=0的近似解,(结果保留两个有效数字)
x
y
1.5
y =x3
y =x+2
答案:X=1.5
(1)二次函数y=ax2+bx+c的图象如图所示,那abc,b2-4ac,2a+b,a+b+c,a-b+c 这五个代数式中,值为正数的有( )
练习
A.4个 B.3个
C.2个 D.1个
y
x
-1
1
y
x
0
2
-3
(2)小明从右边的二次函数y=ax2+bx+c的图象观察得出下面的五条信息:① a< 0;② c=0;③ 函数的最小值为-3; ④当x<0时,y>0; ⑤当0<x1<x2<2时,y1 > y2 你认为其中正确的个数有( )
A.2 B.3
C.4 D.5
(3)请你写出一个二次函数y=ax2+bx+c,使它同时具有如下性质:①图象关于直线x=1对称; ②当x=2时,y>0;③当x=-2时,y<0。
答:____________ ?N!k齉pe剉?螾孴'`( .�p�p�t
二次函数的图象和性质(复习)
(1) 观察右图,h0的值是多少
竖直上抛物体的高度h(m)与运动时间t(s)的关系可用公式 h=-5t2+v0t+h0表示,其中h0(m)是抛出时的高度,v0(m/s) 是抛出时的速度。一个小球从地面以40m/s的速度竖直向上抛出去,小球的高度h(m)与运动时间t(s)的关系如图所示。
(3) 小球何时达到最大高度,
最大高度是多少
0 2 4 6 8
80
60
40
20
t(s)
h(m)
(2) h和t的关系式是 。
(4)小球经过多少秒后落地
例1:
例2:
已知函数 图象如图红色曲线所示。
x
y
o
y=-2
x=-3
(1)若将抛物线 向左平移 3个单位得抛物线 ,
所得的抛物线经怎样平移又得到 的图象。
再向下平移 2 个单位得
抛物线 。
若将抛物线 沿 x 轴向左或向右平移后经过点(3,10),则平移后抛物线的解析式是 。(学生练习)
(2)将抛物线 沿 y 轴向上或向下平移后经过点(3,4),则平移后抛物线的解析式是 ;
x
y
o
(3,5)
Y=5
Y=4
Y=1
x=3
x=1
Y=x2-2x+2
(3,4)
Y=x2-2x+1
已知抛物线 y =ax2+2x+c 经过点(-1,0)、(0,3)
(1)求此抛物线解析式,并在直角坐标系中画出这条抛物线
例3:
·
·
·
·
·
X
y
·
·
X … -2 -1 0 1 2 3 4 …
y =-X2+2X+3 … -5 0 3 4 3 0 -5 …
(2)x取何值时,y 随 x 的增大而增大;
x取何值时,抛物线在 x 轴的上方;
x取何值时,y 随 x 的增大而减小且 y <0。
y =ax2+2x+c
(3)利用图象求方程 ax2+2x+c=-5 解。
(4)若将上题的-5 改为2x-1, 又如何利用图象求方程ax2+2x+c=2x-1的解呢?并比较ax2+2x+c与2x-1的大小。
y =ax2+2x+c
y =2x--1
y1
y2
x
y
·
·
·
·
(5)判断方程 的解的个数。
·
·
·
·
·
·
·
答案:3个
(6)已知函数y =x3 的图象,求方程x3-x-2=0的近似解,(结果保留两个有效数字)
x
y
1.5
y =x3
y =x+2
答案:X=1.5
(1)二次函数y=ax2+bx+c的图象如图所示,那abc,b2-4ac,2a+b,a+b+c,a-b+c 这五个代数式中,值为正数的有( )
练习
A.4个 B.3个
C.2个 D.1个
y
x
-1
1
y
x
0
2
-3
(2)小明从右边的二次函数y=ax2+bx+c的图象观察得出下面的五条信息:① a< 0;② c=0;③ 函数的最小值为-3; ④当x<0时,y>0; ⑤当0<x1<x2<2时,y1 > y2 你认为其中正确的个数有( )
A.2 B.3
C.4 D.5
(3)请你写出一个二次函数y=ax2+bx+c,使它同时具有如下性质:①图象关于直线x=1对称; ②当x=2时,y>0;③当x=-2时,y<0。
答:____________ ?N!k齉pe剉?螾孴'`( .�p�p�t
