2023--2024学年浙教版八年级数学上册 第1章 三角形的初步知识单元测试卷(2)(含答案)
文档属性
| 名称 | 2023--2024学年浙教版八年级数学上册 第1章 三角形的初步知识单元测试卷(2)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 440.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 19:59:32 | ||
图片预览



文档简介
第1章《三角形的初步知识》单元测试卷(2)
本卷满分120分,考试时间120分钟
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列长度的3根小木棒,不能搭成三角形的是( )
A.1 cm,2 cm,3 cm B.2 cm,3 cm,4 cm
C.3 cm,4 cm,5 cm D.4 cm,5 cm,6 cm
2.如图,用尺规作角平分线,根据作图步骤,在说明射线AN是∠BAC的平分线的过程中,错误的是( )
A.由作弧可知AE=AF
B.由作弧可知FP=EP
C.由SAS证明△AFP≌△AEP
D.由△AFP≌△AEP得到∠FAP=∠EAP
3.小桐把一副三角尺按如图所示的方式摆放在一起,其中∠E=∠C=90°,∠A=45°,∠D=30°,∠1=60°,则∠2的度数为( )
A.140° B.150°
C.160° D.170°
4.如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠AED=105°,∠CAD=15°,∠B=30°,则∠1的度数为( )
A.50° B.55°
C.60° D.65°
5.如图,在△ABC中,BC边上的高为h1,在△DEF中,DE边上的高为h2.下列结论中,正确的是( )
A.h1>h2 B.h1C.h1=h2 D.无法确定
6.如图,在△ABC中,已知D,E,F分别是边AC,BD,CE的中点,且阴影部分图形的面积为7,则△ABC的面积为( )
A.14 B.21
C.28 D.32
7.如图,已知△ABC≌△DEF,CD平分∠BCA.若∠A=30°,∠CGF=85°,则∠E的度数为( )
A.35° B.40°
C.45° D.50°
8.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,连结了AC,BD,并设交点为O,得到了如下结论,其中错误的是( )
A.AC⊥BD B.AO=CO=AC
C.△ABD≌△CBD D.AO+DO=BO
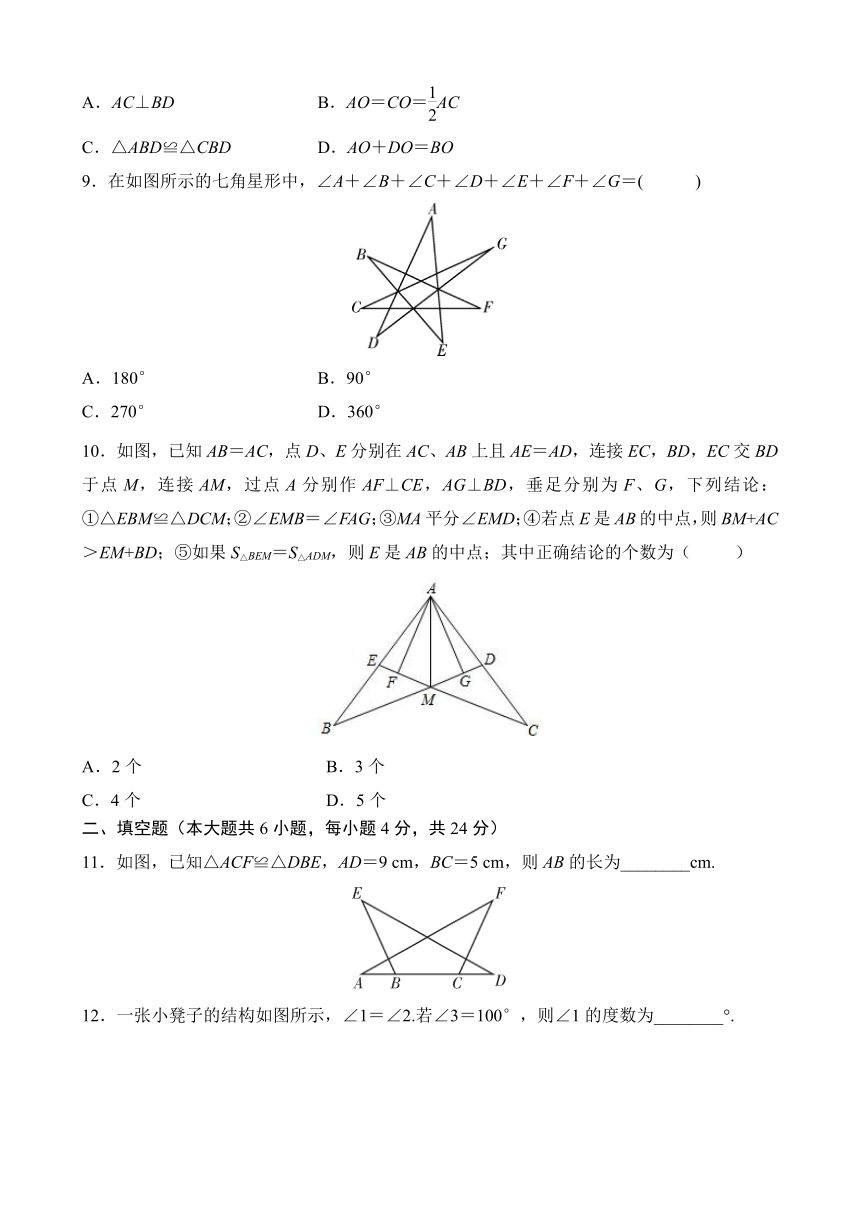
9.在如图所示的七角星形中,∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )
A.180° B.90°
C.270° D.360°
10.如图,已知AB=AC,点D、E分别在AC、AB上且AE=AD,连接EC,BD,EC交BD于点M,连接AM,过点A分别作AF⊥CE,AG⊥BD,垂足分别为F、G,下列结论:①△EBM≌△DCM;②∠EMB=∠FAG;③MA平分∠EMD;④若点E是AB的中点,则BM+AC>EM+BD;⑤如果S△BEM=S△ADM,则E是AB的中点;其中正确结论的个数为( )
A.2个 B.3个
C.4个 D.5个
二、填空题(本大题共6小题,每小题4分,共24分)
11.如图,已知△ACF≌△DBE,AD=9 cm,BC=5 cm,则AB的长为________cm.
12.一张小凳子的结构如图所示,∠1=∠2.若∠3=100°,则∠1的度数为________°.
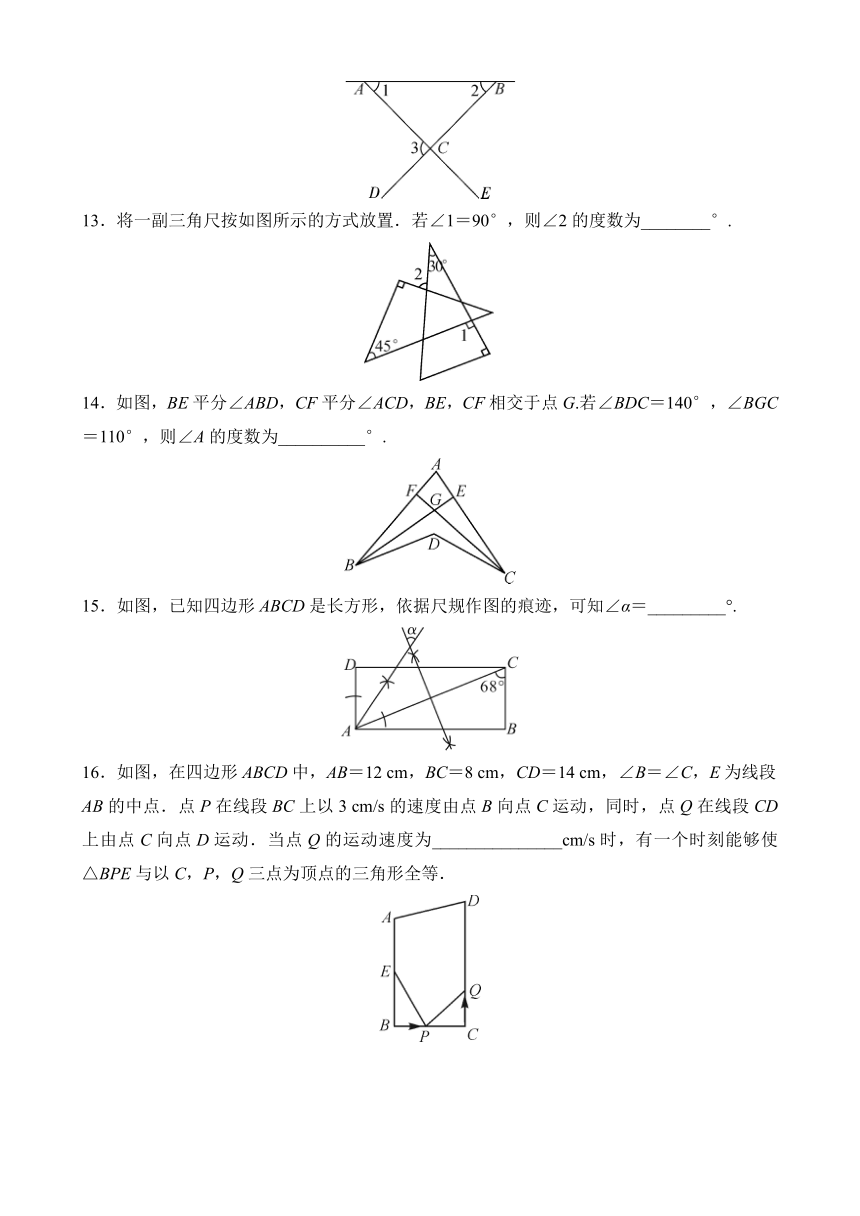
13.将一副三角尺按如图所示的方式放置.若∠1=90°,则∠2的度数为________°.
14.如图,BE平分∠ABD,CF平分∠ACD,BE,CF相交于点G.若∠BDC=140°,∠BGC=110°,则∠A的度数为__________°.
15.如图,已知四边形ABCD是长方形,依据尺规作图的痕迹,可知∠α=_________°.
16.如图,在四边形ABCD中,AB=12 cm,BC=8 cm,CD=14 cm,∠B=∠C,E为线段AB的中点.点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.当点Q的运动速度为_______________cm/s时,有一个时刻能够使△BPE与以C,P,Q三点为顶点的三角形全等.
二、解答题(本大题共8小题,共66分)
17.(本题6分)如图,AC与BD相交于点O,AD=BC,∠D=∠C,求证:BD=AC.
18.(本题6分)一个零件的形状如图所示,已知∠B和∠C应分别是19°和23°,按规定∠A应等于70°这个零件才合格,而某质检员测得∠BDC=111°,就断定这个零件不合格.这是怎么回事呢?聪明的小东想到了原因:延长CD,与AB相交于点E……
请你运用三角形的有关知识帮小东补充完整说理过程.
19.(本题6分)如图,BC的垂直平分线交AB于点D,交BC于点E,已知△ACD的周长是14,AB-AC=2,求AB和AC的长.
20.(本题8分)已知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
21.(本题8分)如图,已知△ABC是直角三角形,∠ACB=90°,AD∥BC,E是线段AC上的一点,AE=BC且DE⊥AB于点F,交AC于点E,连结DC.
(1)求证:AB=DE.
(2)若BC=4,CE=3,求AD的长.
22.(本题10分)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,且BE=BD,连结AE,DE,DC.
(1)求证:△ABE≌△CBD.
(2)若∠CAE=30°,求∠BDC的度数.
23.(本题10分)(1)如图1,A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.求证:DE=BD+CE.
(2)若点A在ED的延长线上,其余条件与(1)相同,如图2,线段DE,BD,CE 之间又有怎样的数量关系?请说明理由.
24.(本题12分)已知在四边形ABCD中,∠DAB+∠BCD=180°,∠ABC+∠ADC=180°,AB=BC,点E,F分别在射线DA,DC上,满足EF=AE+CF.
(1)如图1,若点E,F分别在线段DA,DC上,求证:∠EBF=90°-∠ADC.
(2)如图2,若点E,F分别在线段DA,DC的延长线上,请直接写出∠EBF与∠ADC的数量关系.
答案解析
一、选择题(本大题共10小题,每小题3分,共30分)
1.选A.
2.选C.
3.选B.
4.选C.
【解析】 ∵△ABC≌△ADE,
∴∠ACB=∠AED=105°,
∠D=∠B=30°,
∴∠ACF=180°-∠ACB=75°.
∵∠1+∠D=∠AFG=∠CAD+∠ACF,
即∠1+30°=15°+75°,
∴∠1=60°.
5.选C.
【解析】 如答图,过点A作AM⊥BC于点M,过点F作FN⊥DE,交DE的延长线于点N,则AM=h1,FN=h2.
在△AMC和△FNE中,
∵AM⊥BC,FN⊥DE,
∴∠AMC=∠FNE=90°.
∵∠FED=115°,
∴∠FEN=180°-∠FED=65°=∠ACM.
又∵AC=2.4=FE,
∴△AMC≌△FNE(AAS),
∴AM=FN,即h1=h2.
6.选C.
7.选B.
【解析】 ∵△ABC≌△DEF,
∴∠D=∠A=30°,∠E=∠B,
∴∠BCD=∠CGF-∠D=55°.
又∵CD平分∠BCA,
∴∠BCA=2∠BCD=110°,
∴∠E=∠B=180°-∠A-∠BCA=40°.
8.选D.
9.选A.
【解析】 如答图,设BE,CF,DG相交于点H,AE,BF,DG相交于点P.
由三角形的外角性质,得∠DPE=∠A+∠D,∠EHF=∠B+∠F,∠FHG=∠C+∠G.
又∵∠DPE+∠EHF+∠FHG+∠E=∠HPE+∠EHP+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
10.选D.
【解析】解:①在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠C,
∵AB=AC,AE=AD,
∴AB﹣AE=AC﹣AD,
即BE=CD,
在△EBM和△DCM中,
,
∴△EBM≌△DCM(AAS),
故①正确;
②∵AF⊥CE,AG⊥BD,
∴∠AFM=∠AGM=90°,
∴∠FAG+∠FMG=180°,
∵∠FMG+∠EMB=180°,
∴∠EMB=∠FAG,
故②正确;
③由①知:△EBM≌△DCM,
∴EM=DM,
在△AEM和△ADM中,
,
∴△AEM≌△ADM(SSS),
∴∠AME=∠AMD,
∴MA平分∠EMD;
故③正确;
④如图,延长CE至N,使EN=EM,连接AN,BN,
∵E是AB的中点,
∴AE=BE,
在△AEN和△BEM中,
,
∴△AEN≌△BEM(SAS),
∴AN=BM,
由①知:△ABD≌△ACE,
∴BD=CE,
△ACN中,AC+AN>CN,
∴BM+AC>BD+EM,
故④正确;
⑤∵S△BEM=S△ADM,S△EBM=S△DCM,
∴S△ADM=S△CDM,
∴AD=CDAC,
∵AD=AE,AB=AC,
∴AEAB,
∴E是AB的中点;
故⑤正确;
本题正确的有5个;
故选:D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.答案:2cm.
12.答案:50°.
13.答案:75°.
14.答案:80°.
【解析】 如答图,连结BC.
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABE=∠DBE,∠ACF=∠DCF.
又∵∠BDC=140°,∠BGC=110°,
∴∠DBC+∠DCB=180°-∠BDC=40°,∠GBC+∠GCB=180°-∠BGC=70°,
∴∠ABE+∠ACF=∠DBE+∠DCF=∠GBC-∠DBC+∠GCB-∠DCB=30°,
∴∠ABE+∠ACF+∠GBC+∠GCB=100°,即∠ABC+∠ACB=100°,
∴∠A=180°-(∠ABC+∠ACB)=80°.
15.答案:56°.
【解析】 如答图所示标注字母.
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DAC=∠ACB=68°.
由作法可知,AF是∠DAC的平分线,
∴∠EAF=∠DAC=34°.
由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=180°-∠AEF-∠EAF=56°,
∴∠α=∠AFE=56°.
16.答案:或3cm/s.
【解析】 ∵E为线段AB的中点,AB=12 cm,
∴BE=AB=6 cm.
设运动时间为t(s),点Q的运动速度为v(cm/s),则BP=3t(cm),CQ=vt(cm).
∵BC=8 cm,
∴CP=(8-3t)cm.
又∵∠B=∠C,
∴可分两种情况讨论:
①当△BEP≌△CQP时,
BE=CQ,BP=CP,
∴
解得t=,v=,此时BE=CQ=6 cm,BP=CP=4 cm,符合题意;
②当△BEP≌△CPQ时,
BE=CP,BP=CQ,
∴
解得t=,v=3,此时BE=CP=6 cm,BP=CQ=2 cm,符合题意.
综上所述,当点Q的运动速度为 cm/s 或3 cm/s时,有一个时刻能够使△BPE与以C,P,Q三点为顶点的三角形全等.
二、解答题(本大题共8小题,共66分)
17.(本题6分)
证明:在△OAD和△OBC中,
∵
∴△OAD≌△OBC(AAS),
∴OD=OC,OA=OB,
∴OB+OD=OA+OC,即BD=AC.
18.(本题6分)
解:如答图,延长CD,与AB相交于点E.
∵∠CDB=111°,∠B=19°,∴∠CEB=∠CDB-∠B=111°-19°=92°.
又∵∠C=23°,∴∠A=∠CEB-∠C=92°-23°=69°≠70°,
∴这个零件不合格.
19.(本题6分)
解:∵BC的垂直平分线交AB于点D,
∴DB=DC.
∵△ACD的周长是14,
∴AD+AC+CD=14,即AC+AB=14,
则
解得AB=8,AC=6.
20.(本题8分)
证明:如答图,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠F=∠DEB=90°.
∵∠B+∠ACD=180°,
∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∵
∴△DFC≌△DEB(AAS),
∴DB=DC.
21.(本题8分)
解:(1)∵∠ACB=90°,AD∥BC,
∴∠DAE=180°-∠ACB=90°=∠ACB,
∴∠CAB+∠DAB=90°.
∵DE⊥AB,∴∠AFD=90°,
∴∠ADE+∠DAB=180°-∠AFD=90°,
∴∠CAB=∠ADE.
又∵CB=AE,∴△ABC≌△DEA(AAS),
∴AB=DE.
(2)∵△ABC≌△DEA,
∴CA=AD.
∵AE=BC=4,CE=3,
∴CA=CE+AE=7,
∴AD=7.
22.(本题10分)
解:(1)∵∠ABC=90°,
∴∠CBD=180°-∠ABC=90°.
在△ABE和△CBD中,
∵
∴△ABE≌△CBD(SAS).
(2)如答图,在△ABC中,作AC边上的中线BF,易证△CBF≌△ABF(SSS),
∴∠BCF=∠BAF==45°.
又∵△ABE≌△CBD,∠CAE=30°,
∴∠BDC=∠BEA=∠CAE+∠BCF=75°.
23.(本题10分)
解:(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=180°-∠D=90°.
∵∠BAC=90°,
∴∠DAB+∠EAC=180°-∠BAC=90°,
∴∠DBA=∠EAC.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
(2)DE=BD-CE.理由如下:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=180°-∠ADB=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE-AD=BD-CE.
24.(本题12分)
解:(1)如答图1,延长DA至点H,使AH=CF,连结BH.
∵∠DAB+∠BCD=180°,
∠DAB+∠BAH=180°,
∴∠BCD=∠BAH,即∠BCF=∠BAH.
又∵AB=CB,AH=CF,
∴△HAB≌△FCB(SAS),
∴BH=BF,∠ABH=∠CBF.
又∵EF=AE+CF,
∴EF=AE+AH=EH.
又∵BH=BF,BE=BE,
∴△BEH≌△BEF(SSS),
∴∠EBH=∠EBF,
∴∠EBA+∠CBF=∠EBF,
∴∠EBF=∠ABC=(180°-∠ADC)=90°-∠ADC.
(2)∠EBF=90°+∠ADC.
如答图2,延长CD至点H,使CH=AE,连结BH.
∵∠DAB+∠BCD=180°,
∠DAB+∠BAE=180°,
∴∠BCD=∠BAE,即∠BCH=∠BAE.
又∵AB=CB,AE=CH,
∴△AEB≌△CHB(SAS),
∴BE=BH,∠EBA=∠HBC.
又∵EF=AE+CF,
∴EF=CH+CF=HF.
又∵BF=BF,BE=BH,
∴△EBF≌△HBF(SSS),
∴∠EBF=∠HBF.
∵∠EBF+∠HBF+∠EBA+∠ABH=360°,
∴2∠EBF+∠HBC+∠ABH=360°,
∴2∠EBF+∠ABC=360°,
∴2∠EBF+180°-∠ADC=360°,
∴∠EBF=90°+∠ADC.
本卷满分120分,考试时间120分钟
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列长度的3根小木棒,不能搭成三角形的是( )
A.1 cm,2 cm,3 cm B.2 cm,3 cm,4 cm
C.3 cm,4 cm,5 cm D.4 cm,5 cm,6 cm
2.如图,用尺规作角平分线,根据作图步骤,在说明射线AN是∠BAC的平分线的过程中,错误的是( )
A.由作弧可知AE=AF
B.由作弧可知FP=EP
C.由SAS证明△AFP≌△AEP
D.由△AFP≌△AEP得到∠FAP=∠EAP
3.小桐把一副三角尺按如图所示的方式摆放在一起,其中∠E=∠C=90°,∠A=45°,∠D=30°,∠1=60°,则∠2的度数为( )
A.140° B.150°
C.160° D.170°
4.如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠AED=105°,∠CAD=15°,∠B=30°,则∠1的度数为( )
A.50° B.55°
C.60° D.65°
5.如图,在△ABC中,BC边上的高为h1,在△DEF中,DE边上的高为h2.下列结论中,正确的是( )
A.h1>h2 B.h1
6.如图,在△ABC中,已知D,E,F分别是边AC,BD,CE的中点,且阴影部分图形的面积为7,则△ABC的面积为( )
A.14 B.21
C.28 D.32
7.如图,已知△ABC≌△DEF,CD平分∠BCA.若∠A=30°,∠CGF=85°,则∠E的度数为( )
A.35° B.40°
C.45° D.50°
8.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,连结了AC,BD,并设交点为O,得到了如下结论,其中错误的是( )
A.AC⊥BD B.AO=CO=AC
C.△ABD≌△CBD D.AO+DO=BO
9.在如图所示的七角星形中,∠A+∠B+∠C+∠D+∠E+∠F+∠G=( )
A.180° B.90°
C.270° D.360°
10.如图,已知AB=AC,点D、E分别在AC、AB上且AE=AD,连接EC,BD,EC交BD于点M,连接AM,过点A分别作AF⊥CE,AG⊥BD,垂足分别为F、G,下列结论:①△EBM≌△DCM;②∠EMB=∠FAG;③MA平分∠EMD;④若点E是AB的中点,则BM+AC>EM+BD;⑤如果S△BEM=S△ADM,则E是AB的中点;其中正确结论的个数为( )
A.2个 B.3个
C.4个 D.5个
二、填空题(本大题共6小题,每小题4分,共24分)
11.如图,已知△ACF≌△DBE,AD=9 cm,BC=5 cm,则AB的长为________cm.
12.一张小凳子的结构如图所示,∠1=∠2.若∠3=100°,则∠1的度数为________°.
13.将一副三角尺按如图所示的方式放置.若∠1=90°,则∠2的度数为________°.
14.如图,BE平分∠ABD,CF平分∠ACD,BE,CF相交于点G.若∠BDC=140°,∠BGC=110°,则∠A的度数为__________°.
15.如图,已知四边形ABCD是长方形,依据尺规作图的痕迹,可知∠α=_________°.
16.如图,在四边形ABCD中,AB=12 cm,BC=8 cm,CD=14 cm,∠B=∠C,E为线段AB的中点.点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.当点Q的运动速度为_______________cm/s时,有一个时刻能够使△BPE与以C,P,Q三点为顶点的三角形全等.
二、解答题(本大题共8小题,共66分)
17.(本题6分)如图,AC与BD相交于点O,AD=BC,∠D=∠C,求证:BD=AC.
18.(本题6分)一个零件的形状如图所示,已知∠B和∠C应分别是19°和23°,按规定∠A应等于70°这个零件才合格,而某质检员测得∠BDC=111°,就断定这个零件不合格.这是怎么回事呢?聪明的小东想到了原因:延长CD,与AB相交于点E……
请你运用三角形的有关知识帮小东补充完整说理过程.
19.(本题6分)如图,BC的垂直平分线交AB于点D,交BC于点E,已知△ACD的周长是14,AB-AC=2,求AB和AC的长.
20.(本题8分)已知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
21.(本题8分)如图,已知△ABC是直角三角形,∠ACB=90°,AD∥BC,E是线段AC上的一点,AE=BC且DE⊥AB于点F,交AC于点E,连结DC.
(1)求证:AB=DE.
(2)若BC=4,CE=3,求AD的长.
22.(本题10分)如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,且BE=BD,连结AE,DE,DC.
(1)求证:△ABE≌△CBD.
(2)若∠CAE=30°,求∠BDC的度数.
23.(本题10分)(1)如图1,A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.求证:DE=BD+CE.
(2)若点A在ED的延长线上,其余条件与(1)相同,如图2,线段DE,BD,CE 之间又有怎样的数量关系?请说明理由.
24.(本题12分)已知在四边形ABCD中,∠DAB+∠BCD=180°,∠ABC+∠ADC=180°,AB=BC,点E,F分别在射线DA,DC上,满足EF=AE+CF.
(1)如图1,若点E,F分别在线段DA,DC上,求证:∠EBF=90°-∠ADC.
(2)如图2,若点E,F分别在线段DA,DC的延长线上,请直接写出∠EBF与∠ADC的数量关系.
答案解析
一、选择题(本大题共10小题,每小题3分,共30分)
1.选A.
2.选C.
3.选B.
4.选C.
【解析】 ∵△ABC≌△ADE,
∴∠ACB=∠AED=105°,
∠D=∠B=30°,
∴∠ACF=180°-∠ACB=75°.
∵∠1+∠D=∠AFG=∠CAD+∠ACF,
即∠1+30°=15°+75°,
∴∠1=60°.
5.选C.
【解析】 如答图,过点A作AM⊥BC于点M,过点F作FN⊥DE,交DE的延长线于点N,则AM=h1,FN=h2.
在△AMC和△FNE中,
∵AM⊥BC,FN⊥DE,
∴∠AMC=∠FNE=90°.
∵∠FED=115°,
∴∠FEN=180°-∠FED=65°=∠ACM.
又∵AC=2.4=FE,
∴△AMC≌△FNE(AAS),
∴AM=FN,即h1=h2.
6.选C.
7.选B.
【解析】 ∵△ABC≌△DEF,
∴∠D=∠A=30°,∠E=∠B,
∴∠BCD=∠CGF-∠D=55°.
又∵CD平分∠BCA,
∴∠BCA=2∠BCD=110°,
∴∠E=∠B=180°-∠A-∠BCA=40°.
8.选D.
9.选A.
【解析】 如答图,设BE,CF,DG相交于点H,AE,BF,DG相交于点P.
由三角形的外角性质,得∠DPE=∠A+∠D,∠EHF=∠B+∠F,∠FHG=∠C+∠G.
又∵∠DPE+∠EHF+∠FHG+∠E=∠HPE+∠EHP+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
10.选D.
【解析】解:①在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠C,
∵AB=AC,AE=AD,
∴AB﹣AE=AC﹣AD,
即BE=CD,
在△EBM和△DCM中,
,
∴△EBM≌△DCM(AAS),
故①正确;
②∵AF⊥CE,AG⊥BD,
∴∠AFM=∠AGM=90°,
∴∠FAG+∠FMG=180°,
∵∠FMG+∠EMB=180°,
∴∠EMB=∠FAG,
故②正确;
③由①知:△EBM≌△DCM,
∴EM=DM,
在△AEM和△ADM中,
,
∴△AEM≌△ADM(SSS),
∴∠AME=∠AMD,
∴MA平分∠EMD;
故③正确;
④如图,延长CE至N,使EN=EM,连接AN,BN,
∵E是AB的中点,
∴AE=BE,
在△AEN和△BEM中,
,
∴△AEN≌△BEM(SAS),
∴AN=BM,
由①知:△ABD≌△ACE,
∴BD=CE,
△ACN中,AC+AN>CN,
∴BM+AC>BD+EM,
故④正确;
⑤∵S△BEM=S△ADM,S△EBM=S△DCM,
∴S△ADM=S△CDM,
∴AD=CDAC,
∵AD=AE,AB=AC,
∴AEAB,
∴E是AB的中点;
故⑤正确;
本题正确的有5个;
故选:D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.答案:2cm.
12.答案:50°.
13.答案:75°.
14.答案:80°.
【解析】 如答图,连结BC.
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABE=∠DBE,∠ACF=∠DCF.
又∵∠BDC=140°,∠BGC=110°,
∴∠DBC+∠DCB=180°-∠BDC=40°,∠GBC+∠GCB=180°-∠BGC=70°,
∴∠ABE+∠ACF=∠DBE+∠DCF=∠GBC-∠DBC+∠GCB-∠DCB=30°,
∴∠ABE+∠ACF+∠GBC+∠GCB=100°,即∠ABC+∠ACB=100°,
∴∠A=180°-(∠ABC+∠ACB)=80°.
15.答案:56°.
【解析】 如答图所示标注字母.
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DAC=∠ACB=68°.
由作法可知,AF是∠DAC的平分线,
∴∠EAF=∠DAC=34°.
由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=180°-∠AEF-∠EAF=56°,
∴∠α=∠AFE=56°.
16.答案:或3cm/s.
【解析】 ∵E为线段AB的中点,AB=12 cm,
∴BE=AB=6 cm.
设运动时间为t(s),点Q的运动速度为v(cm/s),则BP=3t(cm),CQ=vt(cm).
∵BC=8 cm,
∴CP=(8-3t)cm.
又∵∠B=∠C,
∴可分两种情况讨论:
①当△BEP≌△CQP时,
BE=CQ,BP=CP,
∴
解得t=,v=,此时BE=CQ=6 cm,BP=CP=4 cm,符合题意;
②当△BEP≌△CPQ时,
BE=CP,BP=CQ,
∴
解得t=,v=3,此时BE=CP=6 cm,BP=CQ=2 cm,符合题意.
综上所述,当点Q的运动速度为 cm/s 或3 cm/s时,有一个时刻能够使△BPE与以C,P,Q三点为顶点的三角形全等.
二、解答题(本大题共8小题,共66分)
17.(本题6分)
证明:在△OAD和△OBC中,
∵
∴△OAD≌△OBC(AAS),
∴OD=OC,OA=OB,
∴OB+OD=OA+OC,即BD=AC.
18.(本题6分)
解:如答图,延长CD,与AB相交于点E.
∵∠CDB=111°,∠B=19°,∴∠CEB=∠CDB-∠B=111°-19°=92°.
又∵∠C=23°,∴∠A=∠CEB-∠C=92°-23°=69°≠70°,
∴这个零件不合格.
19.(本题6分)
解:∵BC的垂直平分线交AB于点D,
∴DB=DC.
∵△ACD的周长是14,
∴AD+AC+CD=14,即AC+AB=14,
则
解得AB=8,AC=6.
20.(本题8分)
证明:如答图,过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠F=∠DEB=90°.
∵∠B+∠ACD=180°,
∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∵
∴△DFC≌△DEB(AAS),
∴DB=DC.
21.(本题8分)
解:(1)∵∠ACB=90°,AD∥BC,
∴∠DAE=180°-∠ACB=90°=∠ACB,
∴∠CAB+∠DAB=90°.
∵DE⊥AB,∴∠AFD=90°,
∴∠ADE+∠DAB=180°-∠AFD=90°,
∴∠CAB=∠ADE.
又∵CB=AE,∴△ABC≌△DEA(AAS),
∴AB=DE.
(2)∵△ABC≌△DEA,
∴CA=AD.
∵AE=BC=4,CE=3,
∴CA=CE+AE=7,
∴AD=7.
22.(本题10分)
解:(1)∵∠ABC=90°,
∴∠CBD=180°-∠ABC=90°.
在△ABE和△CBD中,
∵
∴△ABE≌△CBD(SAS).
(2)如答图,在△ABC中,作AC边上的中线BF,易证△CBF≌△ABF(SSS),
∴∠BCF=∠BAF==45°.
又∵△ABE≌△CBD,∠CAE=30°,
∴∠BDC=∠BEA=∠CAE+∠BCF=75°.
23.(本题10分)
解:(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=180°-∠D=90°.
∵∠BAC=90°,
∴∠DAB+∠EAC=180°-∠BAC=90°,
∴∠DBA=∠EAC.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE+AD=BD+CE.
(2)DE=BD-CE.理由如下:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=180°-∠ADB=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE.
在△ADB和△CEA中,
∵
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,
∴DE=AE-AD=BD-CE.
24.(本题12分)
解:(1)如答图1,延长DA至点H,使AH=CF,连结BH.
∵∠DAB+∠BCD=180°,
∠DAB+∠BAH=180°,
∴∠BCD=∠BAH,即∠BCF=∠BAH.
又∵AB=CB,AH=CF,
∴△HAB≌△FCB(SAS),
∴BH=BF,∠ABH=∠CBF.
又∵EF=AE+CF,
∴EF=AE+AH=EH.
又∵BH=BF,BE=BE,
∴△BEH≌△BEF(SSS),
∴∠EBH=∠EBF,
∴∠EBA+∠CBF=∠EBF,
∴∠EBF=∠ABC=(180°-∠ADC)=90°-∠ADC.
(2)∠EBF=90°+∠ADC.
如答图2,延长CD至点H,使CH=AE,连结BH.
∵∠DAB+∠BCD=180°,
∠DAB+∠BAE=180°,
∴∠BCD=∠BAE,即∠BCH=∠BAE.
又∵AB=CB,AE=CH,
∴△AEB≌△CHB(SAS),
∴BE=BH,∠EBA=∠HBC.
又∵EF=AE+CF,
∴EF=CH+CF=HF.
又∵BF=BF,BE=BH,
∴△EBF≌△HBF(SSS),
∴∠EBF=∠HBF.
∵∠EBF+∠HBF+∠EBA+∠ABH=360°,
∴2∠EBF+∠HBC+∠ABH=360°,
∴2∠EBF+∠ABC=360°,
∴2∠EBF+180°-∠ADC=360°,
∴∠EBF=90°+∠ADC.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
