期末复习—相似三角形

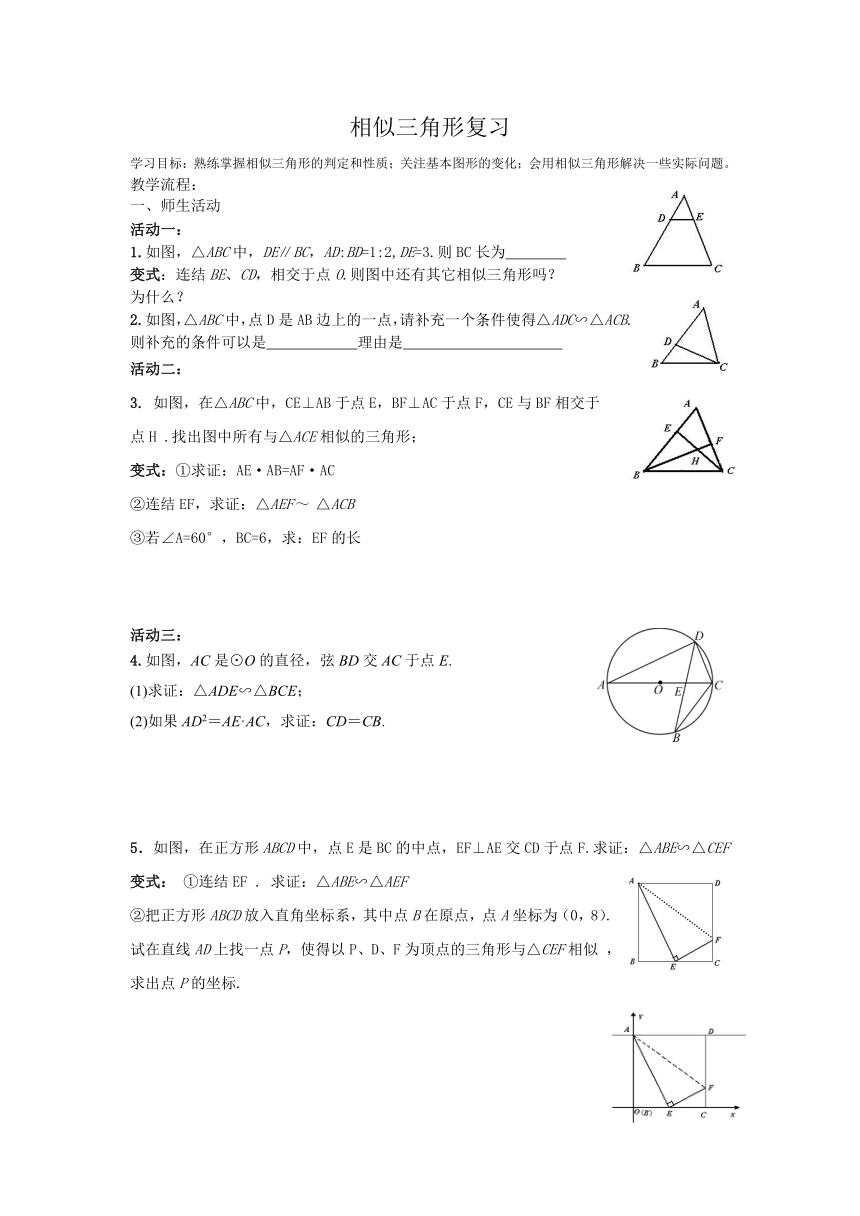
相似三角形复习
学习目标：熟练掌握相似三角形的判定和性质；关注基本图形的变化；会用相似三角形解决一些实际问题。
教学流程：
师生活动
活动一：
1.如图，△ABC中，DE∥BC，AD:BD=1:2,DE=3.则BC长为
变式：连结BE、CD，相交于点O.则图中还有其它相似三角形吗？
为什么？
2.如图，△ABC中，点D是AB边上的一点，请补充一个条件使得△ADC∽△ACB.
则补充的条件可以是 理由是
活动二：
3. 如图，在△ABC中，CE⊥AB于点E，BF⊥AC于点F，CE与BF相交于
点H .找出图中所有与△ACE相似的三角形；
变式：①求证：AE·AB=AF·AC
②连结EF，求证：△AEF～ △ACB
③若∠A=60°，BC=6，求：EF的长
活动三：
4.如图，AC是⊙O的直径，弦BD交AC于点E.
(1)求证：△ADE∽△BCE；
(2)如果AD2＝AE·AC，求证：CD＝CB.
5．如图，在正方形ABCD中，点E是BC的中点，EF⊥AE交CD于点F.求证：△ABE∽△CEF
变式： ①连结EF . 求证：△ABE∽△AEF
②把正方形ABCD放入直角坐标系，其中点 ( http: / / www.21cnjy.com )B在原点，点A坐标为（0，8）. 试在直线AD上找一点P，使得以P、D、F为顶点的三角形与△CEF相似 ，求出点P的坐标.
二、当堂检测
1.如图，△ABC中，BC = 2，DE是它的中位线，下面三个结论：⑴DE=1；
⑵△ADE∽△ABC；⑶△ADE的面积与△ABC的面积之比为1 : 2。
其中正确的有（ ）
A . 0 个 B.1个 C . 2 个 D.3个
2.如图2，△ABC中，点D在边AB上，满足∠ACD =∠ABC，若
AC = 2，AD = 1，则DB = __________.
3．如图4－5－19，在直角三角形ABC中(∠C＝90°)放置边长分别
为3，4，x的三个正方形，则x的值为(　　)
A．5　　　B．6 C．7　　　D．12
4．如图，在△ABC中，∠B＝45°，BC＝5，高AD＝4，矩形EFPQ的一边QP在BC边上，E，F分别在AB，AC上，AD交EF于点H.
(1)求证：＝
(2)设EF＝x，当x为何值时，矩形EFPQ的面积最大？并求出最大面积．
5．如图，直线与抛物线交于A，B两点，点A在x轴上，点B的横坐标为，直线与y轴交于点M。（1）求M点坐标和该抛物线的解析式；
（2）点P是直线AB上方抛物线上一动点（不 ( http: / / www.21cnjy.com )与A，B重合），过点P作x轴的垂线，垂足为点C，交直线AB于点D，作PE⊥AB于点E. 设△PDE的周长为l，点P的横坐标为x，①用含x的代数式表示线段PD的长；
②求l关于x的函数关系式，并求出l的最大值。
C
B
E
D
A
E
B
P
D
M
A
x
O
C
y