第三章 圆的基本性质章末复习----对角互补,四点共圆 课件(共21张PPT)
文档属性
| 名称 | 第三章 圆的基本性质章末复习----对角互补,四点共圆 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 09:09:33 | ||
图片预览


文档简介
(共21张PPT)
浙教版九年级上册
第三章 圆的基本性质章末复习
-----------对角互补
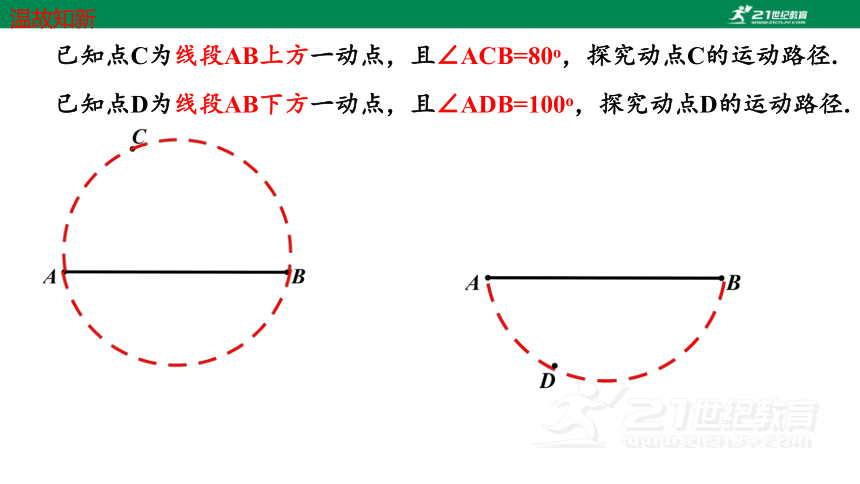
已知点C为线段AB上方一动点,且∠ACB=80o,探究动点C的运动路径.
已知点D为线段AB下方一动点,且∠ADB=100o,探究动点D的运动路径.
温故知新
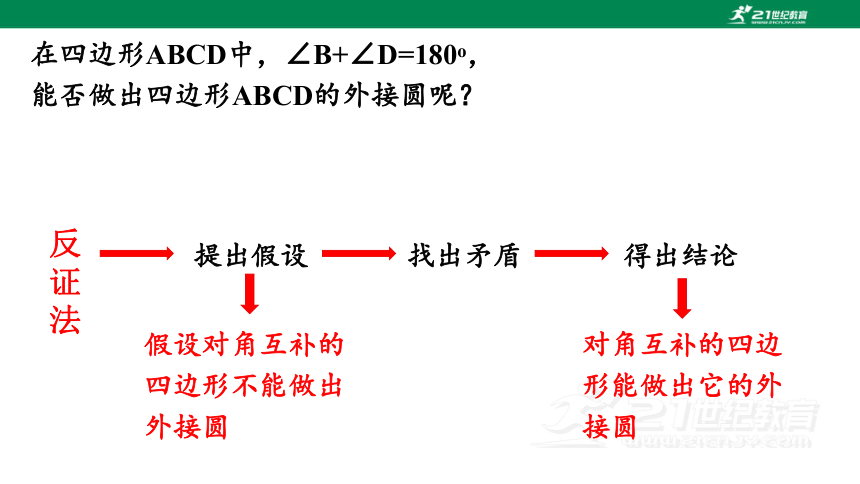
在四边形ABCD中,∠B+∠D=180o,
能否做出四边形ABCD的外接圆呢?
反
证
法
提出假设
假设对角互补的四边形不能做出外接圆
找出矛盾
得出结论
对角互补的四边形能做出它的外接圆
情况一:四边形ABCD,其中点A、B、C三点共圆,点D在圆外.且∠B+∠D=180o.
A
B
C
D
O
E
∵∠B+∠AEC=180o
∠B+∠D=180o.
∴∠AEC=∠D
∵∠AEC>∠D
∴矛盾
情况一矛盾,所以点D不能在圆外.
情况二:四边形ABCD,其中点A、B、C三点共圆,点D在圆内.且∠B+∠D=180o.
A
B
C
D
O
E
∵∠B+∠AEC=180o
∠B+∠ADC=180o.
∴∠AEC=∠ADC
∵∠ADC>∠AEC
∴矛盾
情况二矛盾,所以点D不能在圆内.
结论:点D只能在圆上.
若∠B+∠D=180°,
则点A、B、C、D四点共圆。
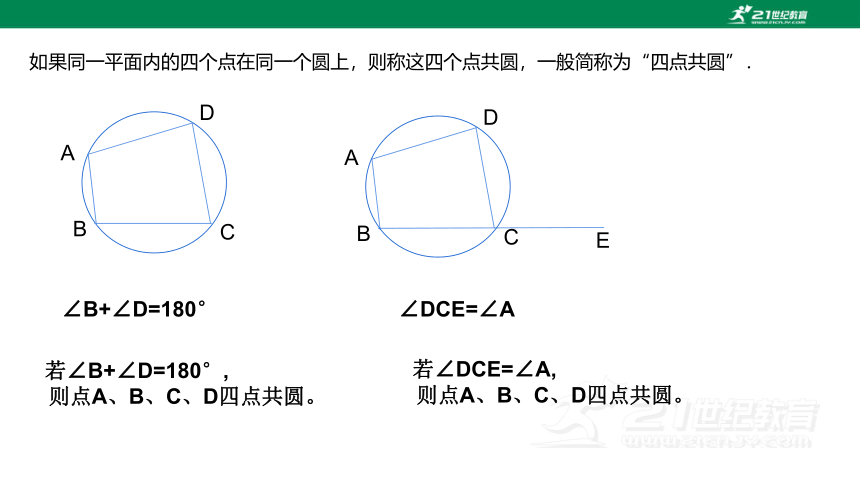
如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”.
∠B+∠D=180°
∠DCE=∠A
A
B
C
D
A
B
C
D
E
若∠DCE=∠A,
则点A、B、C、D四点共圆。
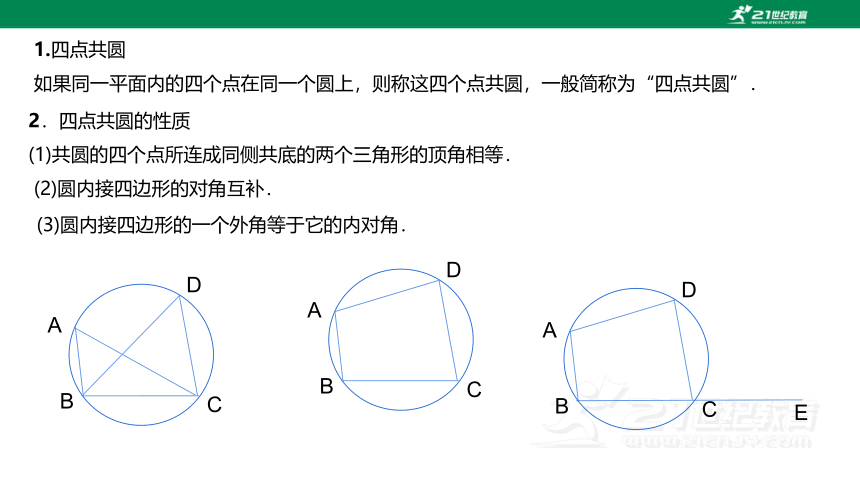
1.四点共圆
如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”.
A
B
C
D
A
B
C
D
E
A
B
C
D
2.四点共圆的性质
(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等.
(2)圆内接四边形的对角互补.
(3)圆内接四边形的一个外角等于它的内对角.
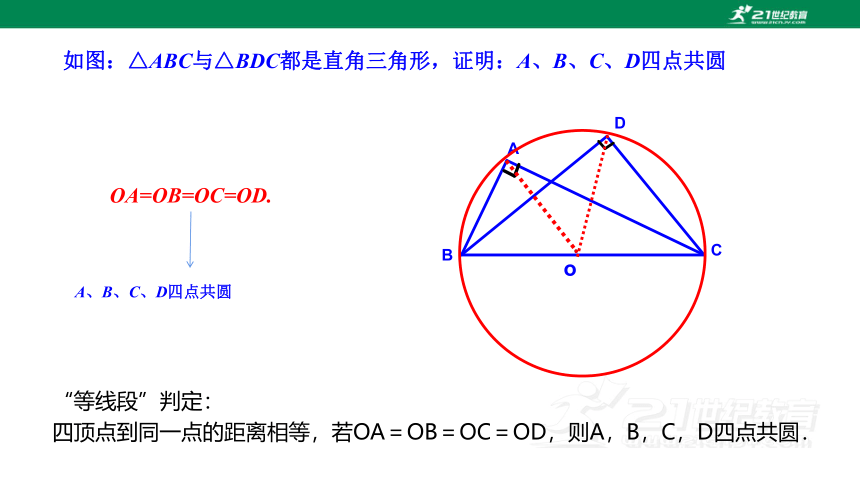
如图:△ABC与△BDC都是直角三角形,证明:A、B、C、D四点共圆
OA=OB=OC=OD.
C
A
D
B
o
A、B、C、D四点共圆
“等线段”判定:
四顶点到同一点的距离相等,若OA=OB=OC=OD,则A,B,C,D四点共圆.
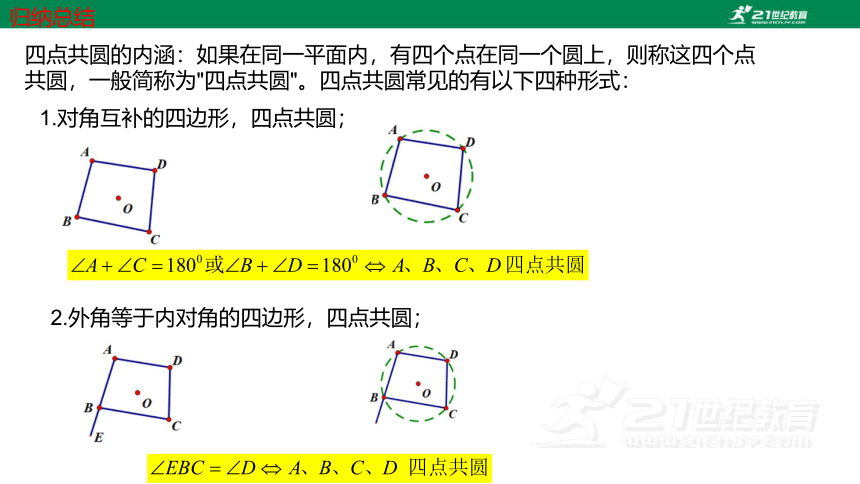
四点共圆的内涵:如果在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为"四点共圆"。四点共圆常见的有以下四种形式:
2.外角等于内对角的四边形,四点共圆;
1.对角互补的四边形,四点共圆;
归纳总结
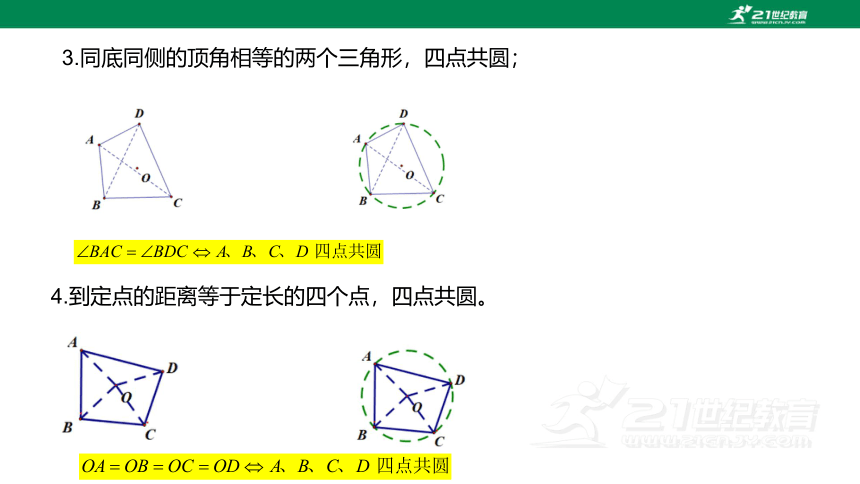
4.到定点的距离等于定长的四个点,四点共圆。
3.同底同侧的顶角相等的两个三角形,四点共圆;
1、在(1)矩形、(2)平行四边形、(3)等腰梯形、(4)菱形中
能过四个顶点作圆的有__________________.
(1) 、(3)
夯实基础,稳扎稳打
2.若EA·ED=EB·EC,则点A、B、C、D四点共圆。
A
B
C
D
E
EA·ED=EB·EC
∠E=∠E
△EAB∽△ECD
∠ECD=∠A
点A、B、C、D四点共圆
3. AD、BE、CF是△ABC的三条高,相交于垂心H,
在A、B、C、D、E、F、H七点中,有几组四点共圆,试逐一举出, 并问各圆心在何处?
4. 如图,平面上有四个点A、O、B、C,
其中∠AOB=1200,∠ACB=600,AO=BO,AB=2 ,
求OC的长
.
连续递推,豁然开朗
配套数字: 1:1:
OC=OA=2
5. 如图,正方形ABCD,点O是对角线AC,BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,求∠OFB的度数.
┛┛
┛
┛
450
450
∠OFB=450
6.如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ABD=72°,求∠CAD的度数
解:∵∠ABC=∠ADC=90°,
∴点A,点B,点C,点D四点共圆,
∴∠ABD=∠ACD=72°,
∴∠CAD=90°﹣∠ACD=18°,
同斜边的直角三角形四点共圆。
7.如图,AB是Rt△ABC和Rt△ABD的公共斜边,AC=BC,∠BAD=320,E是AB的中点,联结DE、CE、CD,求∠ECD的度数
解:∵AB是Rt△ABC和Rt△ABD的公共斜边,
E是AB中点,
∴AE=EB=EC=ED,
∴A、C、B、D在以E为圆心的圆上,
∵∠BAD=32°,
∴∠DCB=∠BAD=32°,
又∵AC=BC,E是Rt△ABC的中点,
∴∠ECB=45°,
∴∠ECD=∠ECB-∠DCB=13°.
320
320
8.如图所示,正方形ABCD中,BD为对角线,点E为BD上一点,过E作EF⊥AE,交DC于F,求证:AE=FE
解:在正方形ABCD中,∠ADC=90°,∠BDC=45°
∵EF⊥AE∴∠AEF=90°
∴∠ADC+∠AEF=180°,A,E,F,D共圆,∴∠EAF=∠BDC=45°,∴∠EAF=∠EFA=45°,AE=EF
.
450
450
9.如图所示,在平行四边形ABCD中,点E为AB,BC的垂直平分线的交点,若∠D=600,求∠AEC.
解:连结EB,
∵点E为AB,BC的垂直平分线的交点
∴EA=EB=EC,
∴A,B,C在以E为圆心,EA为半径的圆上,
作出辅助圆,由圆的性质知
∠AEC=2∠ABC
,又平行四边形ABCD中,
∠ABC=∠D=600
∠AEC=2∠ABC=1200
∴
A
B
C
D
“圆”来如此简单!
“圆”来如此美妙!
“圆”汁“圆”味!
有“圆”千里来相会!
无“圆”对面不相逢!
“圆”形必漏!
“圆”木求鱼!
“圆”“圆”不断!
“圆”来是你!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
第三章 圆的基本性质章末复习
-----------对角互补
已知点C为线段AB上方一动点,且∠ACB=80o,探究动点C的运动路径.
已知点D为线段AB下方一动点,且∠ADB=100o,探究动点D的运动路径.
温故知新
在四边形ABCD中,∠B+∠D=180o,
能否做出四边形ABCD的外接圆呢?
反
证
法
提出假设
假设对角互补的四边形不能做出外接圆
找出矛盾
得出结论
对角互补的四边形能做出它的外接圆
情况一:四边形ABCD,其中点A、B、C三点共圆,点D在圆外.且∠B+∠D=180o.
A
B
C
D
O
E
∵∠B+∠AEC=180o
∠B+∠D=180o.
∴∠AEC=∠D
∵∠AEC>∠D
∴矛盾
情况一矛盾,所以点D不能在圆外.
情况二:四边形ABCD,其中点A、B、C三点共圆,点D在圆内.且∠B+∠D=180o.
A
B
C
D
O
E
∵∠B+∠AEC=180o
∠B+∠ADC=180o.
∴∠AEC=∠ADC
∵∠ADC>∠AEC
∴矛盾
情况二矛盾,所以点D不能在圆内.
结论:点D只能在圆上.
若∠B+∠D=180°,
则点A、B、C、D四点共圆。
如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”.
∠B+∠D=180°
∠DCE=∠A
A
B
C
D
A
B
C
D
E
若∠DCE=∠A,
则点A、B、C、D四点共圆。
1.四点共圆
如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”.
A
B
C
D
A
B
C
D
E
A
B
C
D
2.四点共圆的性质
(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等.
(2)圆内接四边形的对角互补.
(3)圆内接四边形的一个外角等于它的内对角.
如图:△ABC与△BDC都是直角三角形,证明:A、B、C、D四点共圆
OA=OB=OC=OD.
C
A
D
B
o
A、B、C、D四点共圆
“等线段”判定:
四顶点到同一点的距离相等,若OA=OB=OC=OD,则A,B,C,D四点共圆.
四点共圆的内涵:如果在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为"四点共圆"。四点共圆常见的有以下四种形式:
2.外角等于内对角的四边形,四点共圆;
1.对角互补的四边形,四点共圆;
归纳总结
4.到定点的距离等于定长的四个点,四点共圆。
3.同底同侧的顶角相等的两个三角形,四点共圆;
1、在(1)矩形、(2)平行四边形、(3)等腰梯形、(4)菱形中
能过四个顶点作圆的有__________________.
(1) 、(3)
夯实基础,稳扎稳打
2.若EA·ED=EB·EC,则点A、B、C、D四点共圆。
A
B
C
D
E
EA·ED=EB·EC
∠E=∠E
△EAB∽△ECD
∠ECD=∠A
点A、B、C、D四点共圆
3. AD、BE、CF是△ABC的三条高,相交于垂心H,
在A、B、C、D、E、F、H七点中,有几组四点共圆,试逐一举出, 并问各圆心在何处?
4. 如图,平面上有四个点A、O、B、C,
其中∠AOB=1200,∠ACB=600,AO=BO,AB=2 ,
求OC的长
.
连续递推,豁然开朗
配套数字: 1:1:
OC=OA=2
5. 如图,正方形ABCD,点O是对角线AC,BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,求∠OFB的度数.
┛┛
┛
┛
450
450
∠OFB=450
6.如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ABD=72°,求∠CAD的度数
解:∵∠ABC=∠ADC=90°,
∴点A,点B,点C,点D四点共圆,
∴∠ABD=∠ACD=72°,
∴∠CAD=90°﹣∠ACD=18°,
同斜边的直角三角形四点共圆。
7.如图,AB是Rt△ABC和Rt△ABD的公共斜边,AC=BC,∠BAD=320,E是AB的中点,联结DE、CE、CD,求∠ECD的度数
解:∵AB是Rt△ABC和Rt△ABD的公共斜边,
E是AB中点,
∴AE=EB=EC=ED,
∴A、C、B、D在以E为圆心的圆上,
∵∠BAD=32°,
∴∠DCB=∠BAD=32°,
又∵AC=BC,E是Rt△ABC的中点,
∴∠ECB=45°,
∴∠ECD=∠ECB-∠DCB=13°.
320
320
8.如图所示,正方形ABCD中,BD为对角线,点E为BD上一点,过E作EF⊥AE,交DC于F,求证:AE=FE
解:在正方形ABCD中,∠ADC=90°,∠BDC=45°
∵EF⊥AE∴∠AEF=90°
∴∠ADC+∠AEF=180°,A,E,F,D共圆,∴∠EAF=∠BDC=45°,∴∠EAF=∠EFA=45°,AE=EF
.
450
450
9.如图所示,在平行四边形ABCD中,点E为AB,BC的垂直平分线的交点,若∠D=600,求∠AEC.
解:连结EB,
∵点E为AB,BC的垂直平分线的交点
∴EA=EB=EC,
∴A,B,C在以E为圆心,EA为半径的圆上,
作出辅助圆,由圆的性质知
∠AEC=2∠ABC
,又平行四边形ABCD中,
∠ABC=∠D=600
∠AEC=2∠ABC=1200
∴
A
B
C
D
“圆”来如此简单!
“圆”来如此美妙!
“圆”汁“圆”味!
有“圆”千里来相会!
无“圆”对面不相逢!
“圆”形必漏!
“圆”木求鱼!
“圆”“圆”不断!
“圆”来是你!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
