第三章 圆的基本性质章末复习---定弦对定角 课件(共19张PPT)
文档属性
| 名称 | 第三章 圆的基本性质章末复习---定弦对定角 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 09:11:32 | ||
图片预览


文档简介
(共19张PPT)
浙教版九年级上册
第三章 圆的基本性质章末复习
-----------定弦对定角
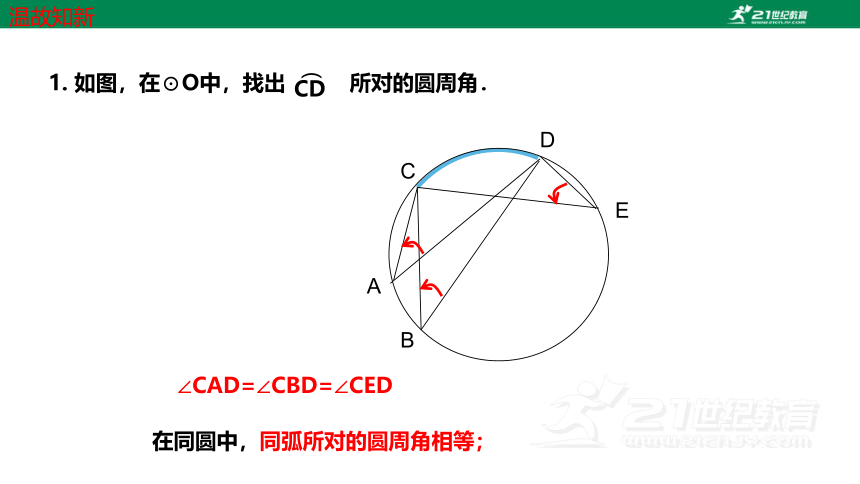
在同圆中,同弧所对的圆周角相等;
∠CAD=∠CBD=∠CED
1. 如图,在⊙O中,找出 所对的圆周角.
CD
(
A
B
C
D
E
温故知新
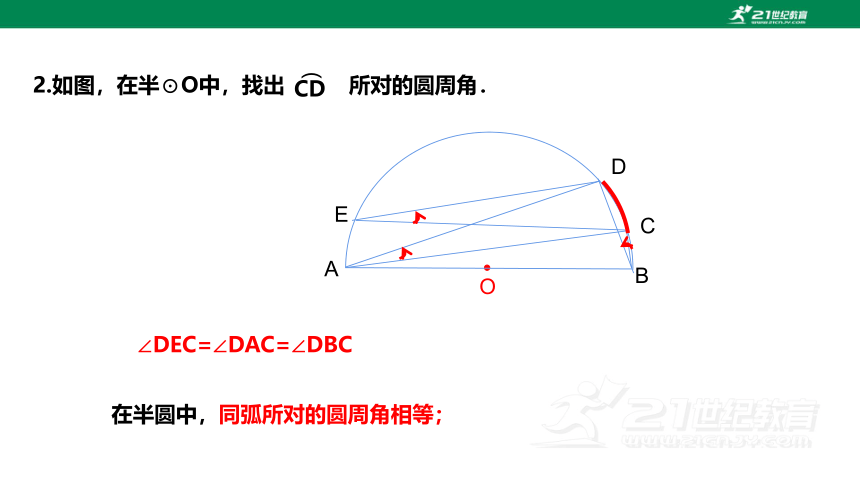
∠DEC=∠DAC=∠DBC
在半圆中,同弧所对的圆周角相等;
O
A
B
E
D
C
2.如图,在半⊙O中,找出 所对的圆周角.
CD
(
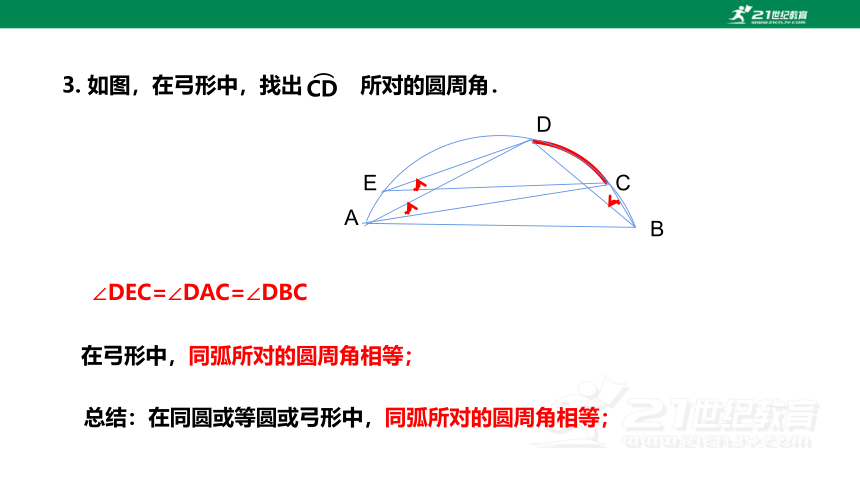
∠DEC=∠DAC=∠DBC
在弓形中,同弧所对的圆周角相等;
3. 如图,在弓形中,找出 所对的圆周角.
CD
(
C
A
D
B
E
总结:在同圆或等圆或弓形中,同弧所对的圆周角相等;
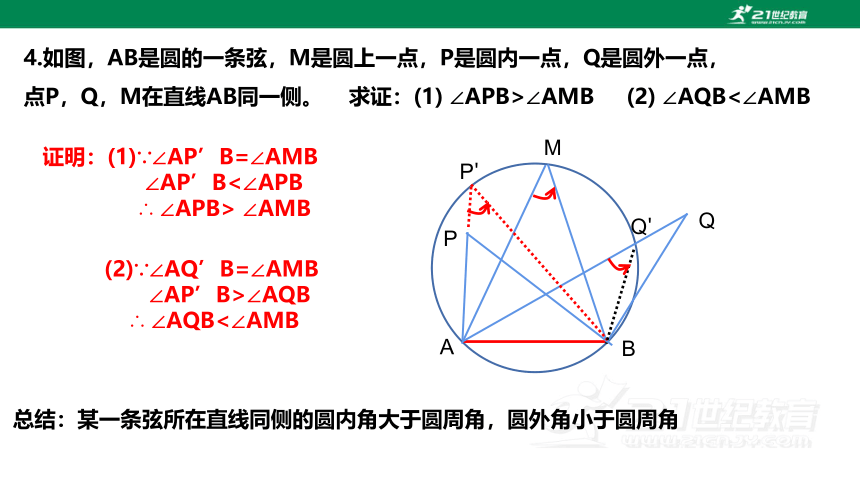
4.如图,AB是圆的一条弦,M是圆上一点,P是圆内一点,Q是圆外一点,
点P,Q,M在直线AB同一侧。 求证:(1) ∠APB>∠AMB (2) ∠AQB<∠AMB
证明:(1)∵∠AP’B=∠AMB
∠AP’B<∠APB
∴ ∠APB> ∠AMB
(2)∵∠AQ’B=∠AMB
∠AP’B>∠AQB
∴ ∠AQB<∠AMB
总结:某一条弦所在直线同侧的圆内角大于圆周角,圆外角小于圆周角
A
B
M
P
Q
P'
Q'
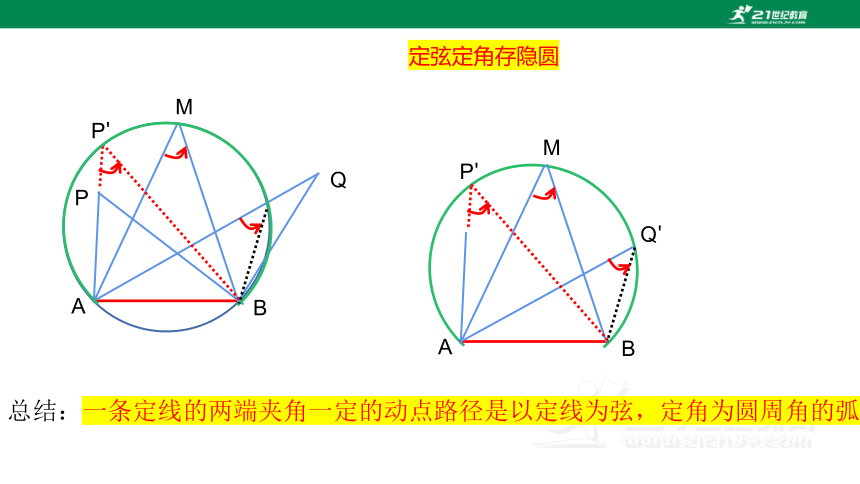
总结:一条定线的两端夹角一定的动点路径是以定线为弦,定角为圆周角的弧
Q'
A
B
M
P'
定弦定角存隐圆
A
B
M
P
Q
P'
1.已知线段BC=2,作△PBC,使∠P=300,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=600时,点P在优弧BPC上,
满足条件的点P有无数个.
B
C
O
P1
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=600
∠P=300,
30°的顶点在动,定长线段位置不变
夯实基础,稳扎稳打
P2
P3
P4
2.已知线段BC=2,作△PBC,使∠P=450,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=900时,点P在优弧BPC上,
满足条件的点有无数个.
B
C
O
P1
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=900
∠P=450
45°的顶点在动,定长线段位置不变
P2
P3
P4
3.已知线段BC=2,作△PBC,使∠P=600,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=1200时,点P在优弧BPC上,
满足条件的点P有无数个.
B
C
O
P
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=1200
∠P=600,
60°的顶点在动,定长线段位置不变
4.已知线段BC=2,作△PBC,使∠P=900,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=1800时,点P在圆上,
满足条件的点P有无数个.
B
C
O
P
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=1800
∠P=900,
90°的顶点在动,定长线段位置不变
2∏
5.已知线段BC=2,用尺规作△PBC,使∠P=1200,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=1200时,点P在劣弧BC上,
满足条件的点P有无数个.
B
C
O
P
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=1200
∠P=1200,
120°的顶点在动,定长线段位置不变
(定角的顶点在动,定长线段位置不变)
题型识别:
有一条长度固定的线段,这条线段所对的张角固定不变。
原理:如图在⊙O中,弦AB所对同侧的圆周角恒相等.
定弦定角存隐圆
6.如图, 点A(2,0),点B(6,0),点P为x轴上方一动点,且∠APB=60o,
求点P的运动路径的长度.
y
x
O
A
B
P
2
6
2
C
∵定弦:线段AB
定角:∠APB=60o
连续递推,豁然开朗
7.在平行四边形ABCD中,AD= ,问AB边上是否存在一个点P,使得 ?若存在,请求出AP的长;若不存在,请说明理由
.
A
B
C
D
P
以B为圆心,BC為半徑画圆交AB于P,
解三角形ABD
8.如图,△ABC为等边三角形,AC=3.若P为△ABC内一动点,
且满足∠PAB=∠ACP,求求点P的运动路径的长度.
.
解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=3,
∵∠PAB=∠ACP,∴∠PAC+∠ACP=60°, ∴∠APC=120°,∴点P的运动轨迹是AC
O
AC=3,
.
∵∠AOC=120°
OA=
.
定弦定角存隐圆
9.在△ABC中,AB=4,∠C=60°,∠A>∠B,求BC的长的取值范围
解题思路:由定角对定长可得点C的运动轨迹,
如图所示,当∠A=∠B时,BC取最小为4,
当BC为直径时,可取最大值为
.
B
C
c
定弦定角存隐圆
10.如图所示,边长为2的等边△ABC的,点B在X轴的正半轴运动,
∠BOD=30°,点A在射线OD上移动,求顶点C到原点的最大距离
解题思路:定角的顶点不动,定长线段位置在变化。
由此可得△OAB的外接圆在变化,但是半径不变,
取任意一个位置作出△OAB的外接圆,
如图所示,此时可取AB的中点F,无论在什么时刻,
OE、EF、CF的长度是不变的,
当点O、E、F、C四点共线时,OC值取最大,
最大值为:OE+EF+CF=2+2
思维拓展,更上一层
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
第三章 圆的基本性质章末复习
-----------定弦对定角
在同圆中,同弧所对的圆周角相等;
∠CAD=∠CBD=∠CED
1. 如图,在⊙O中,找出 所对的圆周角.
CD
(
A
B
C
D
E
温故知新
∠DEC=∠DAC=∠DBC
在半圆中,同弧所对的圆周角相等;
O
A
B
E
D
C
2.如图,在半⊙O中,找出 所对的圆周角.
CD
(
∠DEC=∠DAC=∠DBC
在弓形中,同弧所对的圆周角相等;
3. 如图,在弓形中,找出 所对的圆周角.
CD
(
C
A
D
B
E
总结:在同圆或等圆或弓形中,同弧所对的圆周角相等;
4.如图,AB是圆的一条弦,M是圆上一点,P是圆内一点,Q是圆外一点,
点P,Q,M在直线AB同一侧。 求证:(1) ∠APB>∠AMB (2) ∠AQB<∠AMB
证明:(1)∵∠AP’B=∠AMB
∠AP’B<∠APB
∴ ∠APB> ∠AMB
(2)∵∠AQ’B=∠AMB
∠AP’B>∠AQB
∴ ∠AQB<∠AMB
总结:某一条弦所在直线同侧的圆内角大于圆周角,圆外角小于圆周角
A
B
M
P
Q
P'
Q'
总结:一条定线的两端夹角一定的动点路径是以定线为弦,定角为圆周角的弧
Q'
A
B
M
P'
定弦定角存隐圆
A
B
M
P
Q
P'
1.已知线段BC=2,作△PBC,使∠P=300,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=600时,点P在优弧BPC上,
满足条件的点P有无数个.
B
C
O
P1
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=600
∠P=300,
30°的顶点在动,定长线段位置不变
夯实基础,稳扎稳打
P2
P3
P4
2.已知线段BC=2,作△PBC,使∠P=450,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=900时,点P在优弧BPC上,
满足条件的点有无数个.
B
C
O
P1
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=900
∠P=450
45°的顶点在动,定长线段位置不变
P2
P3
P4
3.已知线段BC=2,作△PBC,使∠P=600,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=1200时,点P在优弧BPC上,
满足条件的点P有无数个.
B
C
O
P
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=1200
∠P=600,
60°的顶点在动,定长线段位置不变
4.已知线段BC=2,作△PBC,使∠P=900,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=1800时,点P在圆上,
满足条件的点P有无数个.
B
C
O
P
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=1800
∠P=900,
90°的顶点在动,定长线段位置不变
2∏
5.已知线段BC=2,用尺规作△PBC,使∠P=1200,你能作出多少个满足条件的三角形?
当BC=2,∠BOC=1200时,点P在劣弧BC上,
满足条件的点P有无数个.
B
C
O
P
有一条长度固定的线段,这条线段所对的张角固定不变。
点P的运动路径的长度
∠BOC=1200
∠P=1200,
120°的顶点在动,定长线段位置不变
(定角的顶点在动,定长线段位置不变)
题型识别:
有一条长度固定的线段,这条线段所对的张角固定不变。
原理:如图在⊙O中,弦AB所对同侧的圆周角恒相等.
定弦定角存隐圆
6.如图, 点A(2,0),点B(6,0),点P为x轴上方一动点,且∠APB=60o,
求点P的运动路径的长度.
y
x
O
A
B
P
2
6
2
C
∵定弦:线段AB
定角:∠APB=60o
连续递推,豁然开朗
7.在平行四边形ABCD中,AD= ,问AB边上是否存在一个点P,使得 ?若存在,请求出AP的长;若不存在,请说明理由
.
A
B
C
D
P
以B为圆心,BC為半徑画圆交AB于P,
解三角形ABD
8.如图,△ABC为等边三角形,AC=3.若P为△ABC内一动点,
且满足∠PAB=∠ACP,求求点P的运动路径的长度.
.
解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=3,
∵∠PAB=∠ACP,∴∠PAC+∠ACP=60°, ∴∠APC=120°,∴点P的运动轨迹是AC
O
AC=3,
.
∵∠AOC=120°
OA=
.
定弦定角存隐圆
9.在△ABC中,AB=4,∠C=60°,∠A>∠B,求BC的长的取值范围
解题思路:由定角对定长可得点C的运动轨迹,
如图所示,当∠A=∠B时,BC取最小为4,
当BC为直径时,可取最大值为
.
B
C
c
定弦定角存隐圆
10.如图所示,边长为2的等边△ABC的,点B在X轴的正半轴运动,
∠BOD=30°,点A在射线OD上移动,求顶点C到原点的最大距离
解题思路:定角的顶点不动,定长线段位置在变化。
由此可得△OAB的外接圆在变化,但是半径不变,
取任意一个位置作出△OAB的外接圆,
如图所示,此时可取AB的中点F,无论在什么时刻,
OE、EF、CF的长度是不变的,
当点O、E、F、C四点共线时,OC值取最大,
最大值为:OE+EF+CF=2+2
思维拓展,更上一层
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
