第三章 圆的基本性质章末复习-----直角对直径 课件(共16张PPT)
文档属性
| 名称 | 第三章 圆的基本性质章末复习-----直角对直径 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 09:12:49 | ||
图片预览

文档简介
(共16张PPT)
浙教版九年级上册
第三章
第三章 圆的基本性质章末复习
-----------直角对直径
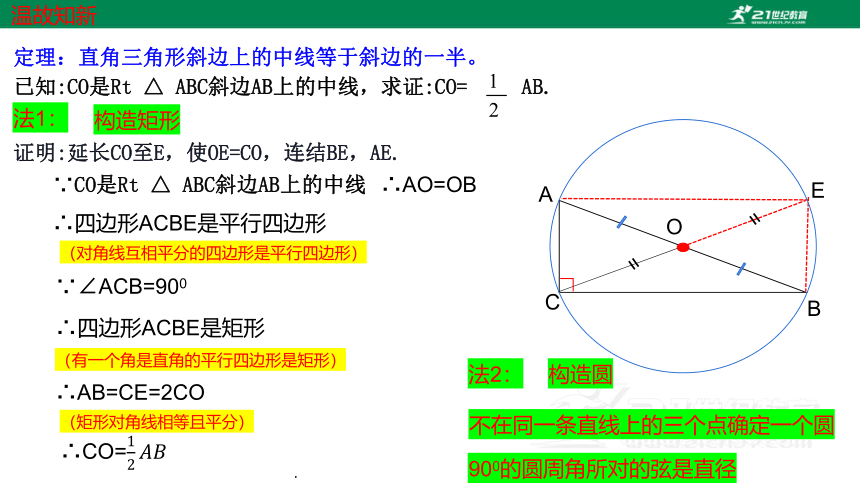
定理:直角三角形斜边上的中线等于斜边的一半。
已知:CO是Rt △ ABC斜边AB上的中线,求证:CO= AB.
证明:延长CO至E,使OE=CO,连结BE,AE.
∵CO是Rt △ ABC斜边AB上的中线
∴AO=OB
∴四边形ACBE是平行四边形
∵∠ACB=900
∴四边形ACBE是矩形
∴AB=CE=2CO
A
B
C
O
∟
E
=
=
(对角线互相平分的四边形是平行四边形)
(有一个角是直角的平行四边形是矩形)
(矩形对角线相等且平分)
∴CO=
.
900的圆周角所对的弦是直径
法1:
法2:
构造矩形
构造圆
不在同一条直线上的三个点确定一个圆
温故知新
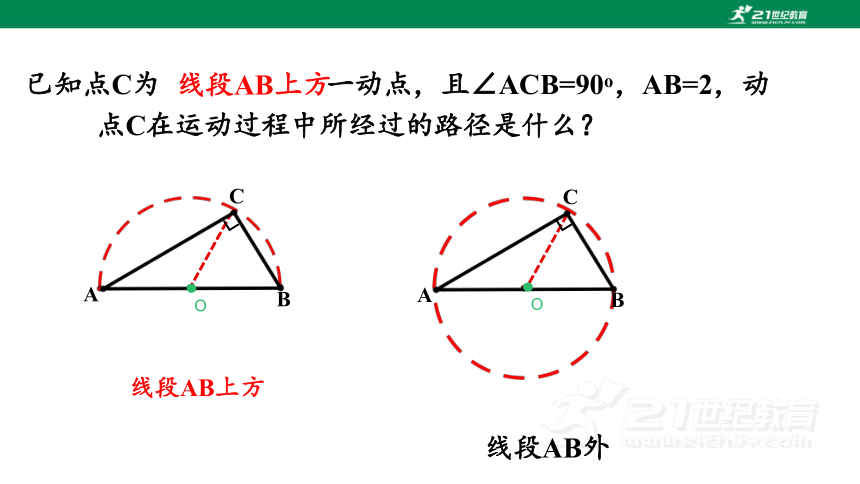
已知点C为 一动点,且∠ACB=90o,AB=2,动
点C在运动过程中所经过的路径是什么?
线段AB上方
线段AB外
线段AB上方
C
A
B
C
A
B
O
O
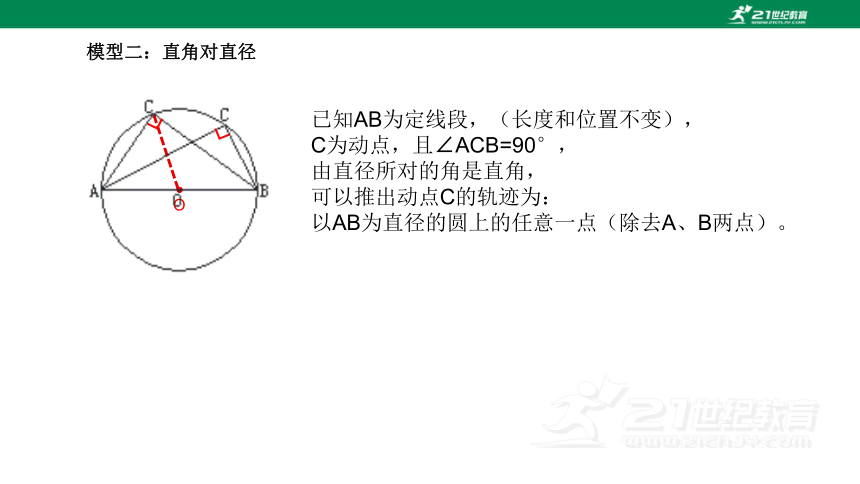
模型二:直角对直径
已知AB为定线段,(长度和位置不变),
C为动点,且∠ACB=90°,
由直径所对的角是直角,
可以推出动点C的轨迹为:
以AB为直径的圆上的任意一点(除去A、B两点)。
O
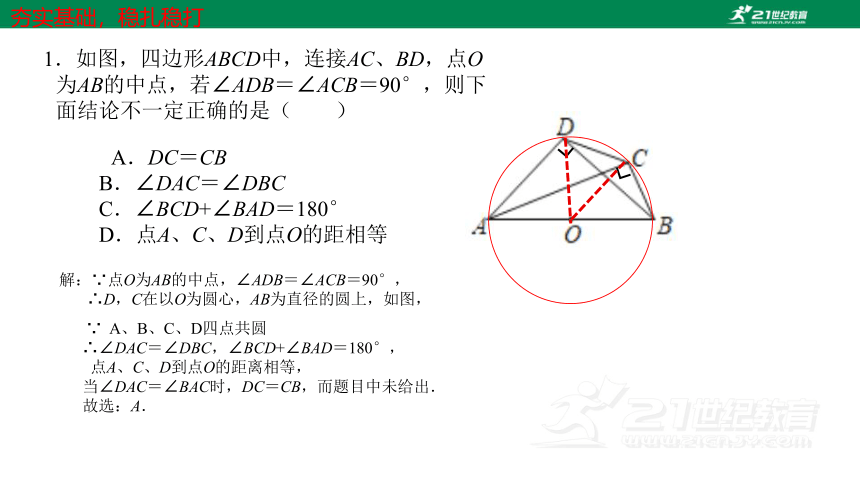
1.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距相等
解:∵点O为AB的中点,∠ADB=∠ACB=90°,
∴D,C在以O为圆心,AB为直径的圆上,如图,
∵ A、B、C、D四点共圆
∴∠DAC=∠DBC,∠BCD+∠BAD=180°,
点A、C、D到点O的距离相等,
当∠DAC=∠BAC时,DC=CB,而题目中未给出.
故选:A.
夯实基础,稳扎稳打
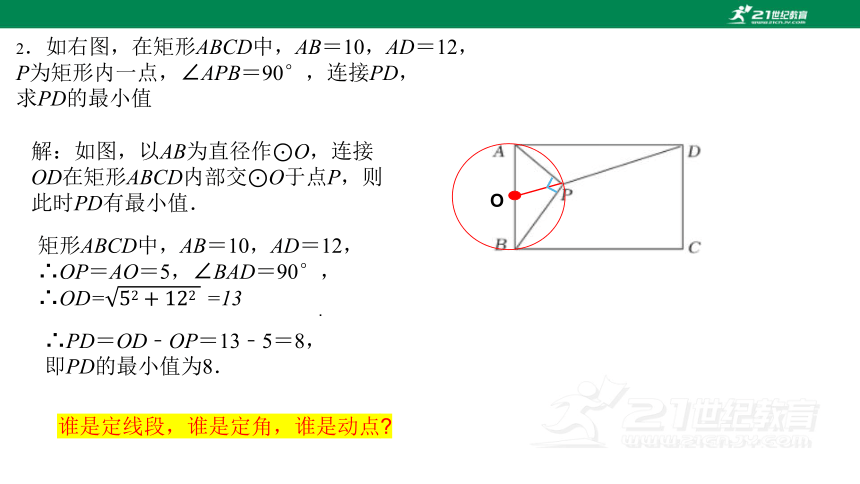
2.如右图,在矩形ABCD中,AB=10,AD=12,
P为矩形内一点,∠APB=90°,连接PD,
求PD的最小值
解:如图,以AB为直径作⊙O,连接OD在矩形ABCD内部交⊙O于点P,则此时PD有最小值.
∴PD=OD﹣OP=13﹣5=8,
即PD的最小值为8.
矩形ABCD中,AB=10,AD=12,
∴OP=AO=5,∠BAD=90°,
∴OD= =13
.
O
谁是定线段,谁是定角,谁是动点
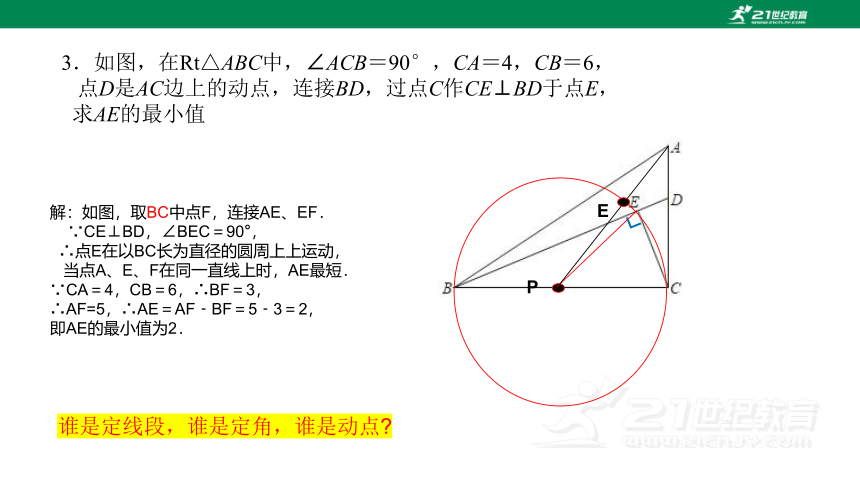
3.如图,在Rt△ABC中,∠ACB=90°,CA=4,CB=6,
点D是AC边上的动点,连接BD,过点C作CE⊥BD于点E,
求AE的最小值
解:如图,取BC中点F,连接AE、EF.
∵CE⊥BD,∠BEC=90°,
∴点E在以BC长为直径的圆周上上运动,
当点A、E、F在同一直线上时,AE最短.
∵CA=4,CB=6,∴BF=3,
∴AF=5,∴AE=AF﹣BF=5﹣3=2,
即AE的最小值为2.
P
E
谁是定线段,谁是定角,谁是动点
4.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
P是△ABC内部的一个动点,且满足∠PAC=∠PCB,
求线段PB的最小值
解:∵∠ACB=90°,∴∠ACP+∠PCB=90°,
∵∠PAC=∠PCB,∴∠CAP+∠ACP=90°,∴∠APC=90°,
∴点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,
在Rt△CBO中,∠OCB=90°,BC=3,OC=2,
∴OB= =
.
∴PB=OB﹣OP=
.
∴PB最小值为
.
O
谁是定线段,谁是定角,谁是动点
连续递推,豁然开朗
5.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,求线段DP的最小值
O
P
OP=1
OD=
.
PD
.
点P的路径是一段以AB为直径的弧
△ABE ≌△DAF
∠APB=900
6.如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,求CP的最小值
O
P
-2
7.如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=900时,连接PD,求线段PD的最小值。
点P在以AB为直径的圆弧上
O
P
PD最小值=
OP=2
∠ACB=1200
∠DBC=300
∠ABD=900
BD=4
.
8.如图,AB是半圆O的直径,AB=10,弦AC长为8,点D是弧BC上一个动点,连接AD,作CE⊥AD,垂足为E,连接BE,则BE的最小值是_______________.
P
E
9.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,求MD+MP的最小值
如图,作点D关于BC的对称点D',连接PD'
D'
O
P的轨迹为以AB为直径的四分之一圆弧上
MD+MP的最小值:
P
G
思维拓展,更上一层
10.如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,
把△PAB沿着AP翻折到△PB'C(点B'在矩形的内部),连接B'C,B'D.点P在整个运动过程中,若存在唯一的位置使得△B'CD为直角三角形,求a,b之间的数量关系
O
a>0,b>0
B'
如图,以CD为直径作 ,当点A到 的最小距离等于AB时,
使得△为直角三角形且唯一,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
第三章
第三章 圆的基本性质章末复习
-----------直角对直径
定理:直角三角形斜边上的中线等于斜边的一半。
已知:CO是Rt △ ABC斜边AB上的中线,求证:CO= AB.
证明:延长CO至E,使OE=CO,连结BE,AE.
∵CO是Rt △ ABC斜边AB上的中线
∴AO=OB
∴四边形ACBE是平行四边形
∵∠ACB=900
∴四边形ACBE是矩形
∴AB=CE=2CO
A
B
C
O
∟
E
=
=
(对角线互相平分的四边形是平行四边形)
(有一个角是直角的平行四边形是矩形)
(矩形对角线相等且平分)
∴CO=
.
900的圆周角所对的弦是直径
法1:
法2:
构造矩形
构造圆
不在同一条直线上的三个点确定一个圆
温故知新
已知点C为 一动点,且∠ACB=90o,AB=2,动
点C在运动过程中所经过的路径是什么?
线段AB上方
线段AB外
线段AB上方
C
A
B
C
A
B
O
O
模型二:直角对直径
已知AB为定线段,(长度和位置不变),
C为动点,且∠ACB=90°,
由直径所对的角是直角,
可以推出动点C的轨迹为:
以AB为直径的圆上的任意一点(除去A、B两点)。
O
1.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距相等
解:∵点O为AB的中点,∠ADB=∠ACB=90°,
∴D,C在以O为圆心,AB为直径的圆上,如图,
∵ A、B、C、D四点共圆
∴∠DAC=∠DBC,∠BCD+∠BAD=180°,
点A、C、D到点O的距离相等,
当∠DAC=∠BAC时,DC=CB,而题目中未给出.
故选:A.
夯实基础,稳扎稳打
2.如右图,在矩形ABCD中,AB=10,AD=12,
P为矩形内一点,∠APB=90°,连接PD,
求PD的最小值
解:如图,以AB为直径作⊙O,连接OD在矩形ABCD内部交⊙O于点P,则此时PD有最小值.
∴PD=OD﹣OP=13﹣5=8,
即PD的最小值为8.
矩形ABCD中,AB=10,AD=12,
∴OP=AO=5,∠BAD=90°,
∴OD= =13
.
O
谁是定线段,谁是定角,谁是动点
3.如图,在Rt△ABC中,∠ACB=90°,CA=4,CB=6,
点D是AC边上的动点,连接BD,过点C作CE⊥BD于点E,
求AE的最小值
解:如图,取BC中点F,连接AE、EF.
∵CE⊥BD,∠BEC=90°,
∴点E在以BC长为直径的圆周上上运动,
当点A、E、F在同一直线上时,AE最短.
∵CA=4,CB=6,∴BF=3,
∴AF=5,∴AE=AF﹣BF=5﹣3=2,
即AE的最小值为2.
P
E
谁是定线段,谁是定角,谁是动点
4.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
P是△ABC内部的一个动点,且满足∠PAC=∠PCB,
求线段PB的最小值
解:∵∠ACB=90°,∴∠ACP+∠PCB=90°,
∵∠PAC=∠PCB,∴∠CAP+∠ACP=90°,∴∠APC=90°,
∴点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,
在Rt△CBO中,∠OCB=90°,BC=3,OC=2,
∴OB= =
.
∴PB=OB﹣OP=
.
∴PB最小值为
.
O
谁是定线段,谁是定角,谁是动点
连续递推,豁然开朗
5.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,求线段DP的最小值
O
P
OP=1
OD=
.
PD
.
点P的路径是一段以AB为直径的弧
△ABE ≌△DAF
∠APB=900
6.如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,求CP的最小值
O
P
-2
7.如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=900时,连接PD,求线段PD的最小值。
点P在以AB为直径的圆弧上
O
P
PD最小值=
OP=2
∠ACB=1200
∠DBC=300
∠ABD=900
BD=4
.
8.如图,AB是半圆O的直径,AB=10,弦AC长为8,点D是弧BC上一个动点,连接AD,作CE⊥AD,垂足为E,连接BE,则BE的最小值是_______________.
P
E
9.如图,正方形ABCD中,AB=2,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,求MD+MP的最小值
如图,作点D关于BC的对称点D',连接PD'
D'
O
P的轨迹为以AB为直径的四分之一圆弧上
MD+MP的最小值:
P
G
思维拓展,更上一层
10.如图,在矩形ABCD中,AB=a,BC=b,点P是BC上的一个动点,连接AP,
把△PAB沿着AP翻折到△PB'C(点B'在矩形的内部),连接B'C,B'D.点P在整个运动过程中,若存在唯一的位置使得△B'CD为直角三角形,求a,b之间的数量关系
O
a>0,b>0
B'
如图,以CD为直径作 ,当点A到 的最小距离等于AB时,
使得△为直角三角形且唯一,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
