3.7正多边形随堂练习(无答案)浙教版数学九年级上册
文档属性
| 名称 | 3.7正多边形随堂练习(无答案)浙教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 717.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-02 00:00:00 | ||
图片预览


文档简介
3.7正多边形随堂练习-浙教版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,若已知该外接圆的半径是4,则正六边形的面积是( )
A. B.24 C. D.
2.如图,正边形两条对角线、的延长线交于点,若,则的值是( )
A.12 B.15 C.18 D.24
3.一个正六边形的半径为R,边心距为r,那么R与r的关系是( )
A.r=R B.r=R C.r=R D.r=R
4.如图,是的内接正三角形,四边形是的内接正四边形,若线段恰是的一个内接正边形的一条边,则( )
A. B. C. D.
5.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为
A.6, B.,3 C.6,3 D.,
6.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为( )cm.
A.2 B.2 C. D.4
7.一元钱硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大不能超过( )
A.12 mm B.12 mm
C.6 mm D.6 mm
8.如图,正六边形,,点P从点A出发,沿以每秒1个单位长度的速度运动,当运动到第秒时,的面积为( )
A. B. C. D.1
9.一般地,如果在一次实验中,结果落在区域D中每一个点都是等可能的,用A表示“实验结果落在D中的某个小区域M中”这个事件,那么事件A发生的概率.如图,现向等边的外接圆区域内射入一个点,则该点落在内的概率是( )
A. B. C. D.
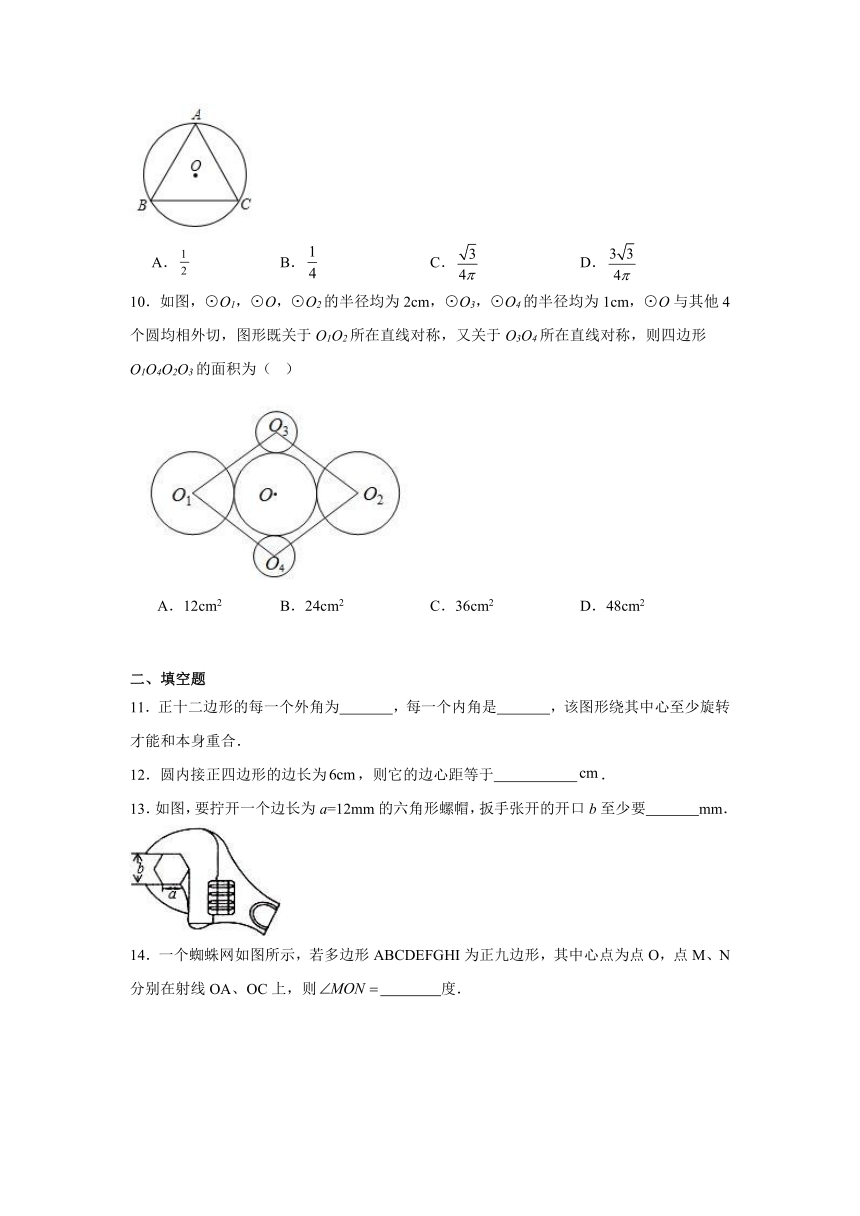
10.如图,⊙O1,⊙O,⊙O2的半径均为2cm,⊙O3,⊙O4的半径均为1cm,⊙O与其他4个圆均相外切,图形既关于O1O2所在直线对称,又关于O3O4所在直线对称,则四边形O1O4O2O3的面积为( )
A.12cm2 B.24cm2 C.36cm2 D.48cm2
二、填空题
11.正十二边形的每一个外角为 ,每一个内角是 ,该图形绕其中心至少旋转 才能和本身重合.
12.圆内接正四边形的边长为,则它的边心距等于 .
13.如图,要拧开一个边长为a=12mm的六角形螺帽,扳手张开的开口b至少要 mm.
14.一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则 度.
15.边长为6的正三角形的外接圆的周长为 .
16.正六边形的中心角等于 度.
17.边长为6的正六边形的外接圆的面积为 .
18.若正六边形的周长为6,则它的面积为 .
19.如图,万名塔,位于凤凰古城沙湾的沱江之滨,于1988年建成,该塔是一个六角塔,如果它的地基是半径为2米的正六边形,那么这个地基的周长是 米.
20.边长为4cm的正六边形,它的内切圆与外接圆半径的比值是_____.
三、解答题
21.如图,把边长为6的正三角形剪去三个三角形得到一个正六边形,求这个正六边形的面积.
22.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
23.将正三角形ABC各边三等分,设分点为D、E、F、G、H、I,
求证:DEFGHI是正六边形.
24.如图①,正六边形ABCDEF的边长为a,P是BC上一动点,过P作PMAB交AF于M,作PNCD交DE于N.
(1)求出的度数,并证明;
(2)如图②,点是的中点,连接、,求证:;
(3)如图③,点O是AD的中点,OG平分,求证:四边形OMGN是菱形.
25.如图,正五边形的两条对角线相交于点F.
(1)求的度数;
(2)求证:四边形为菱形.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,若已知该外接圆的半径是4,则正六边形的面积是( )
A. B.24 C. D.
2.如图,正边形两条对角线、的延长线交于点,若,则的值是( )
A.12 B.15 C.18 D.24
3.一个正六边形的半径为R,边心距为r,那么R与r的关系是( )
A.r=R B.r=R C.r=R D.r=R
4.如图,是的内接正三角形,四边形是的内接正四边形,若线段恰是的一个内接正边形的一条边,则( )
A. B. C. D.
5.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为
A.6, B.,3 C.6,3 D.,
6.已知正六边形ABCDEF的边心距为 cm,则正六边形的半径为( )cm.
A.2 B.2 C. D.4
7.一元钱硬币的直径约为24 mm,则用它能完全覆盖住的正六边形的边长最大不能超过( )
A.12 mm B.12 mm
C.6 mm D.6 mm
8.如图,正六边形,,点P从点A出发,沿以每秒1个单位长度的速度运动,当运动到第秒时,的面积为( )
A. B. C. D.1
9.一般地,如果在一次实验中,结果落在区域D中每一个点都是等可能的,用A表示“实验结果落在D中的某个小区域M中”这个事件,那么事件A发生的概率.如图,现向等边的外接圆区域内射入一个点,则该点落在内的概率是( )
A. B. C. D.
10.如图,⊙O1,⊙O,⊙O2的半径均为2cm,⊙O3,⊙O4的半径均为1cm,⊙O与其他4个圆均相外切,图形既关于O1O2所在直线对称,又关于O3O4所在直线对称,则四边形O1O4O2O3的面积为( )
A.12cm2 B.24cm2 C.36cm2 D.48cm2
二、填空题
11.正十二边形的每一个外角为 ,每一个内角是 ,该图形绕其中心至少旋转 才能和本身重合.
12.圆内接正四边形的边长为,则它的边心距等于 .
13.如图,要拧开一个边长为a=12mm的六角形螺帽,扳手张开的开口b至少要 mm.
14.一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则 度.
15.边长为6的正三角形的外接圆的周长为 .
16.正六边形的中心角等于 度.
17.边长为6的正六边形的外接圆的面积为 .
18.若正六边形的周长为6,则它的面积为 .
19.如图,万名塔,位于凤凰古城沙湾的沱江之滨,于1988年建成,该塔是一个六角塔,如果它的地基是半径为2米的正六边形,那么这个地基的周长是 米.
20.边长为4cm的正六边形,它的内切圆与外接圆半径的比值是_____.
三、解答题
21.如图,把边长为6的正三角形剪去三个三角形得到一个正六边形,求这个正六边形的面积.
22.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:PA=PC+ PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
23.将正三角形ABC各边三等分,设分点为D、E、F、G、H、I,
求证:DEFGHI是正六边形.
24.如图①,正六边形ABCDEF的边长为a,P是BC上一动点,过P作PMAB交AF于M,作PNCD交DE于N.
(1)求出的度数,并证明;
(2)如图②,点是的中点,连接、,求证:;
(3)如图③,点O是AD的中点,OG平分,求证:四边形OMGN是菱形.
25.如图,正五边形的两条对角线相交于点F.
(1)求的度数;
(2)求证:四边形为菱形.
同课章节目录
