一元二次方程解法(浙江省温州市)

课件14张PPT。一元二次方程的
解法举例富春三中八年级数学组 ①因式分解法
②直接开平方法
③公式法
④配方法
（方程一边是0，另一边整式容易因式分解）（ (x+m)2=k k≥0 ）(化方程为一般式）（二次项系数为1，而一次项系数为偶数）解一元二次方程的方法方法1方法2方法3解:移项,得
方程左边因式分解,得
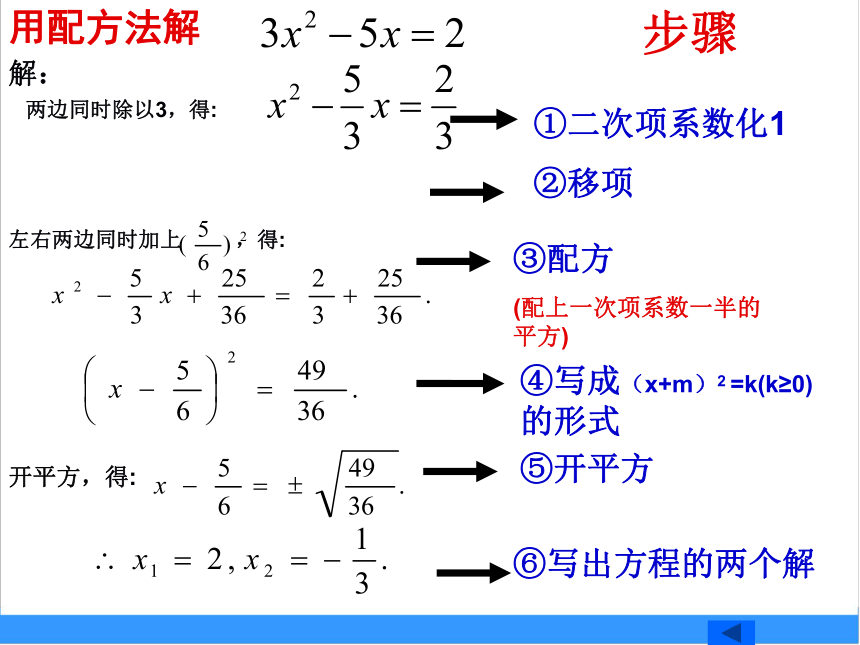
解题步骤用因式分解法解用配方法解解：两边同时除以3，得:左右两边同时加上 ，得:开平方，得:步骤用公式法解解:移项,得
这里a=3,b=-5,c=-2=49解题步骤例1.选择适当的方法解下列方程：①
②
③结论先考虑开平方法,
再用因式分解法;
最后才用公式法和配方法.请你选择恰当的方法解方程　
①　(x-1)(x+1)=x
②　x (2x+5)=2 (2x+5)
③　(2x－1)2=4(x+3)2
④　3(x-2)2－9=0试一试能不能用整体
思想？例2. 解方程

② 2(x-2)2+5(x-2)-3=0
总结：方程中有括号时，应先用整体思想考虑有没有简单方法，若看不出合适的方法时，则把它去括号并整理为一般形式再选取合理的方法。变1： 2(x-2)2+5(2-x)-3=0再变为： 2(x-2)2+5x-13=02(x-2)2+5x-10-3=0变2： 2(2-x)2+5(2-x)-3=0① (2m+3)2=2(4m+7)比一比谁最快：谈谈你的收获能力拓展解关于x的方程：①②小结：ax2+c=0 ====>ax2+bx=0 ====>ax2+bx+c=0 ====>因式分解法公式法（配方法）2、公式法虽然是万能的，对任何一元二次方程都适用，但不一定 是最简单的，因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法，若不行，再考虑公式法（适当也可考虑配方法）3、方程中有括号时，应先用整体思想考虑有没有简单方法，若看不出合适的方法时，则把它去括号并整理为一般形式再选取合理的方法。1、直接开平方法因式分解法结束寄语配方法和公式法是解一元二次方程重要方法,要作为一种基本技能来掌握.
一元二次方程也是刻画现实世界的有效数学模型.