第一章 二次函数章末复习----建立适当的坐标系课件(共18张PPT)
文档属性
| 名称 | 第一章 二次函数章末复习----建立适当的坐标系课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
浙教版九年级上册
第一章 二次函数章末复习
----建立适当的坐标系
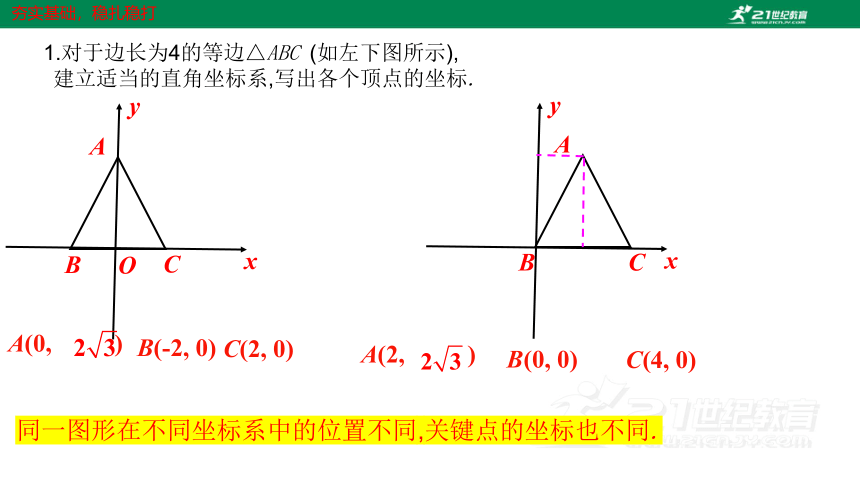
1.对于边长为4的等边△ABC (如左下图所示),
建立适当的直角坐标系,写出各个顶点的坐标.
同一图形在不同坐标系中的位置不同,关键点的坐标也不同.
C
A
B
x
y
O
A(0, )
B(-2, 0)
C(2, 0)
C
A
B
x
y
A(2, )
B(0, 0)
C(4, 0)
夯实基础,稳扎稳打
对于边长为4的等边△ABC(如左下图所示),
建立适当的直角坐标系,写出各个顶点的坐标.
同一图形在不同坐标系中的位置不同,关键点的坐标也不同.
C
A
B
x
y
A(0, 0)
C
A
B
x
y
A(-2, )
B(-4, 0)
C(0, 0)
B(-2, - )
C(2,- )
C
A
B
x
y
O
A(0, )
B(-2, 0)
C(2, 0)
C
A
B
x
y
A(2, )
B(0, 0)
C(4, 0)
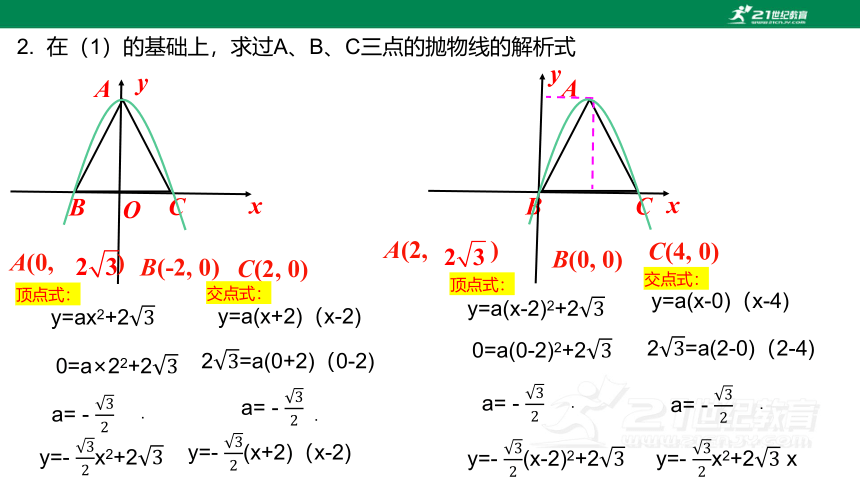
2. 在(1)的基础上,求过A、B、C三点的抛物线的解析式
y=ax2+2
0=a×22+2
a= -
.
y=- x2+2
.
y=a(x+2)(x-2)
2=a(0+2)(0-2)
a= -
.
y=- (x+2)(x-2)
.
y=a(x-2)2+2
0=a(0-2)2+2
a= -
.
y=- (x-2)2+2
y=a(x-0)(x-4)
2=a(2-0)(2-4)
a= -
.
y=- x2+2 x
.
顶点式:
交点式:
顶点式:
交点式:
C
A
B
x
y
A(-2, )
B(-4, 0)
C(0, 0)
C
A
B
x
y
A(0, 0)
B(-2, - )
C(2,- )
y=ax2
-2=a×22
a= -
.
y=- x2
.
y=a(x+2)2+2
0=a(0+2)2+2
a= -
.
y=- (x+2)2+2
y=a(x-0)(x+4)
2=a(-2-0)(-2+4)
a= -
.
y=- x2 -2 x
.
交点式:
顶点式:
顶点式:
2.如何选择不同形式的二次函数的关系式?
1. 一般式
(已知抛物线上三点或三对x、y的值,用一般式.)
2.顶点式:
(已知抛物线的顶点或对称轴或最值,用顶点式.)
3.交点式 :
(已知抛物线与 x 轴两交点的坐标,用交点式。)
3.位于中国贵州省内的射电望远镜(FAST)是目前世界上口径最大、精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点C到口径面AB的距离是100米.若按如图2建立平面直角坐标系,求抛物线的解析式
A(-250,0),B(250,0),C(0,-100)
y=ax2-100
0=a×2502-100
a=
.
y=x2-100
.
y=a(x+250)(x-250)
-100=a(0+250)(0-250)
a=
.
y=(x+250)(x-250)
y=x2-100
.
顶点式:
交点式:
4.图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,
灯罩D距离地面1.86 m,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,求茶几到灯柱的距离AE的长度.
x
y
O
y=a(x-1.5)2+2.5
A(0,0), B(0,1.5),C(1.5.2.5)
1.5=a(0-1.5)2+2.5
a= -
.
y= - (x-1.5)2+2.5
.
(x-1.5)2=1.44
.
1.86= - (x-1.5)2+2.5
.
x1=2.7, x2=0.3(舍去)
连续递推,豁然开朗
5.如示,一拱桥的截面呈抛物线形状,拱桥两端点与水面的距离都是1m,拱桥的跨度为10m,拱桥与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.
(1)建立适当的平面直角坐标系并求出抛物线对应的函数表达式;
(2)求两盏景观灯之间的水平距离.
x
y
O
解:(1)如图:顶点坐标是(5,5),与y轴的交点坐标是(0,1).
设y=a(x-5)2+5,1=a(0-5)2+5,
得a=- y=- (x-5)2+5(0≤x≤10).
.
(2)由已知得两盏景观灯的纵坐标都是4,
令4=- (x-5)2+5,∴x1= ,x2=
∴两盏景观灯之间的水平距离为 =5(m).
.
x
y
O
y=ax2
(5, -4)
-4=a×52
a= -
.
两盏景观灯的纵坐标都是-1,
x1= ,x2=-
.
y=- x2
.
-1=- x2
.
两盏景观灯之间的水平距离为=5(m)
.
6.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状.身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,求绳子的最低点到地面的距离.
x
y
O
y=a(x-1)2+k
7.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,
求在线段AB上离中心M处5米的地方桥的高度
x
y
O
x
y
O
顶点坐标是(20,16),
设y=a(x-20)2+16, 0=a(0-20)2+16,
得a=- y=- (x-20)2+16.
.
当X=25时,y=- (25-20)2+16=12.
.
y=ax2
(20, -16)
-16=a×202
a= -
.
当X=5时,y=- 52=-4
.
16-4=12
y=- x2
.
8. 某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为1.6米,求他在不弯腰的情况下在大棚里活动的范围.
x
y
O
x
y
O
顶点坐标是(2.5,2),
设y=a(x-2.5)2+2, 0=a(0-2.5)2+2,
得a=- y=- (x-2.5)2+2.
.
当y=1.6时,1.6=- (x-2.5)2+2.
.
x1=
x2=
x1-x2=
.
y=ax2
(2.5, -2)
-2=a×2.52
a= -
.
当y=-0.4时,- x2=-0.4
.
x1=
x2=
x1-x2=
.
y=- x2
.
9. 如图,某公园草坪的防护栏形状是抛物线型.为了安全起见,每段防护栏要间距0.4 m架设一根不锈钢的支柱,防护栏的最高点距离底部0.5 m.
(1)建立适当的平面直角坐标系,求防护栏所在抛物线对应的函数解析式;
(2)根据(1)中求得的函数解析式,求防护栏支柱A3B3的长度.
(0,0.5),(1,0),
设y=ax2+0.5,a=-0.5,
y=-0.5x2+0.5
x
y
O
当x=0.2时,y=-0.5×0.22+0.5=0.48,
“建系”是灵活应用二次函数解决实际问题的一种方法
在解决实际问题时,我们应建立简单方便的平面直角坐标系.
10.随着新农村的建设和旧城的改造,我们的家园越来越美丽.小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少.
y=a(x-1)2+k(0≤x≤3).
y=(x-1)2+(0≤x≤3).
思维拓展,更上一层
11.平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,求学生丁的身高
x
y
O
(-1,1),(0,1.5),(3,1),
y=ax2+,
.
当x=1.5时,代入求出y=1.625
.
y=-x2+,
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
第一章 二次函数章末复习
----建立适当的坐标系
1.对于边长为4的等边△ABC (如左下图所示),
建立适当的直角坐标系,写出各个顶点的坐标.
同一图形在不同坐标系中的位置不同,关键点的坐标也不同.
C
A
B
x
y
O
A(0, )
B(-2, 0)
C(2, 0)
C
A
B
x
y
A(2, )
B(0, 0)
C(4, 0)
夯实基础,稳扎稳打
对于边长为4的等边△ABC(如左下图所示),
建立适当的直角坐标系,写出各个顶点的坐标.
同一图形在不同坐标系中的位置不同,关键点的坐标也不同.
C
A
B
x
y
A(0, 0)
C
A
B
x
y
A(-2, )
B(-4, 0)
C(0, 0)
B(-2, - )
C(2,- )
C
A
B
x
y
O
A(0, )
B(-2, 0)
C(2, 0)
C
A
B
x
y
A(2, )
B(0, 0)
C(4, 0)
2. 在(1)的基础上,求过A、B、C三点的抛物线的解析式
y=ax2+2
0=a×22+2
a= -
.
y=- x2+2
.
y=a(x+2)(x-2)
2=a(0+2)(0-2)
a= -
.
y=- (x+2)(x-2)
.
y=a(x-2)2+2
0=a(0-2)2+2
a= -
.
y=- (x-2)2+2
y=a(x-0)(x-4)
2=a(2-0)(2-4)
a= -
.
y=- x2+2 x
.
顶点式:
交点式:
顶点式:
交点式:
C
A
B
x
y
A(-2, )
B(-4, 0)
C(0, 0)
C
A
B
x
y
A(0, 0)
B(-2, - )
C(2,- )
y=ax2
-2=a×22
a= -
.
y=- x2
.
y=a(x+2)2+2
0=a(0+2)2+2
a= -
.
y=- (x+2)2+2
y=a(x-0)(x+4)
2=a(-2-0)(-2+4)
a= -
.
y=- x2 -2 x
.
交点式:
顶点式:
顶点式:
2.如何选择不同形式的二次函数的关系式?
1. 一般式
(已知抛物线上三点或三对x、y的值,用一般式.)
2.顶点式:
(已知抛物线的顶点或对称轴或最值,用顶点式.)
3.交点式 :
(已知抛物线与 x 轴两交点的坐标,用交点式。)
3.位于中国贵州省内的射电望远镜(FAST)是目前世界上口径最大、精度最高的望远镜.根据有关资料显示,该望远镜的轴截面呈抛物线状,口径AB为500米,最低点C到口径面AB的距离是100米.若按如图2建立平面直角坐标系,求抛物线的解析式
A(-250,0),B(250,0),C(0,-100)
y=ax2-100
0=a×2502-100
a=
.
y=x2-100
.
y=a(x+250)(x-250)
-100=a(0+250)(0-250)
a=
.
y=(x+250)(x-250)
y=x2-100
.
顶点式:
交点式:
4.图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,
灯罩D距离地面1.86 m,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,求茶几到灯柱的距离AE的长度.
x
y
O
y=a(x-1.5)2+2.5
A(0,0), B(0,1.5),C(1.5.2.5)
1.5=a(0-1.5)2+2.5
a= -
.
y= - (x-1.5)2+2.5
.
(x-1.5)2=1.44
.
1.86= - (x-1.5)2+2.5
.
x1=2.7, x2=0.3(舍去)
连续递推,豁然开朗
5.如示,一拱桥的截面呈抛物线形状,拱桥两端点与水面的距离都是1m,拱桥的跨度为10m,拱桥与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.
(1)建立适当的平面直角坐标系并求出抛物线对应的函数表达式;
(2)求两盏景观灯之间的水平距离.
x
y
O
解:(1)如图:顶点坐标是(5,5),与y轴的交点坐标是(0,1).
设y=a(x-5)2+5,1=a(0-5)2+5,
得a=- y=- (x-5)2+5(0≤x≤10).
.
(2)由已知得两盏景观灯的纵坐标都是4,
令4=- (x-5)2+5,∴x1= ,x2=
∴两盏景观灯之间的水平距离为 =5(m).
.
x
y
O
y=ax2
(5, -4)
-4=a×52
a= -
.
两盏景观灯的纵坐标都是-1,
x1= ,x2=-
.
y=- x2
.
-1=- x2
.
两盏景观灯之间的水平距离为=5(m)
.
6.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状.身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,求绳子的最低点到地面的距离.
x
y
O
y=a(x-1)2+k
7.如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,
求在线段AB上离中心M处5米的地方桥的高度
x
y
O
x
y
O
顶点坐标是(20,16),
设y=a(x-20)2+16, 0=a(0-20)2+16,
得a=- y=- (x-20)2+16.
.
当X=25时,y=- (25-20)2+16=12.
.
y=ax2
(20, -16)
-16=a×202
a= -
.
当X=5时,y=- 52=-4
.
16-4=12
y=- x2
.
8. 某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为1.6米,求他在不弯腰的情况下在大棚里活动的范围.
x
y
O
x
y
O
顶点坐标是(2.5,2),
设y=a(x-2.5)2+2, 0=a(0-2.5)2+2,
得a=- y=- (x-2.5)2+2.
.
当y=1.6时,1.6=- (x-2.5)2+2.
.
x1=
x2=
x1-x2=
.
y=ax2
(2.5, -2)
-2=a×2.52
a= -
.
当y=-0.4时,- x2=-0.4
.
x1=
x2=
x1-x2=
.
y=- x2
.
9. 如图,某公园草坪的防护栏形状是抛物线型.为了安全起见,每段防护栏要间距0.4 m架设一根不锈钢的支柱,防护栏的最高点距离底部0.5 m.
(1)建立适当的平面直角坐标系,求防护栏所在抛物线对应的函数解析式;
(2)根据(1)中求得的函数解析式,求防护栏支柱A3B3的长度.
(0,0.5),(1,0),
设y=ax2+0.5,a=-0.5,
y=-0.5x2+0.5
x
y
O
当x=0.2时,y=-0.5×0.22+0.5=0.48,
“建系”是灵活应用二次函数解决实际问题的一种方法
在解决实际问题时,我们应建立简单方便的平面直角坐标系.
10.随着新农村的建设和旧城的改造,我们的家园越来越美丽.小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少.
y=a(x-1)2+k(0≤x≤3).
y=(x-1)2+(0≤x≤3).
思维拓展,更上一层
11.平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,求学生丁的身高
x
y
O
(-1,1),(0,1.5),(3,1),
y=ax2+,
.
当x=1.5时,代入求出y=1.625
.
y=-x2+,
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
