4.6 相似多边形课件(共22张PPT)
文档属性
| 名称 | 4.6 相似多边形课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-03 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
浙教版九年级上册
4.6 相似多边形
第四章 相似三角形
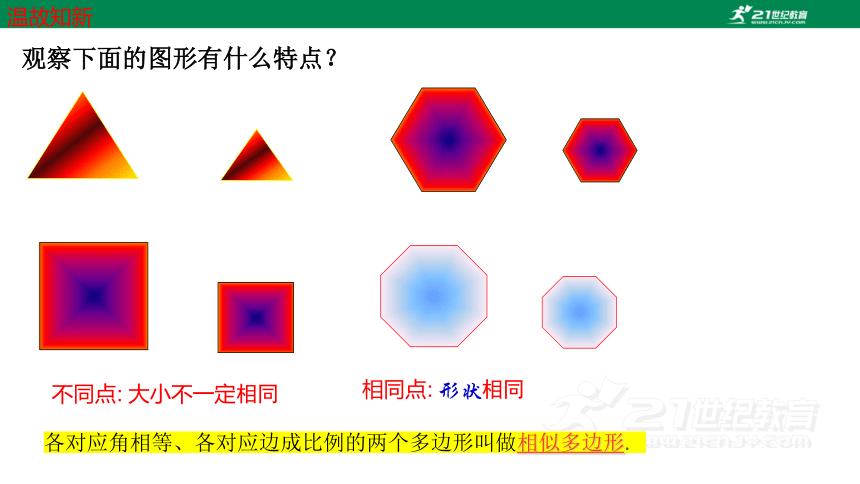
观察下面的图形有什么特点?
相同点: 形状相同
不同点: 大小不一定相同
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
温故知新
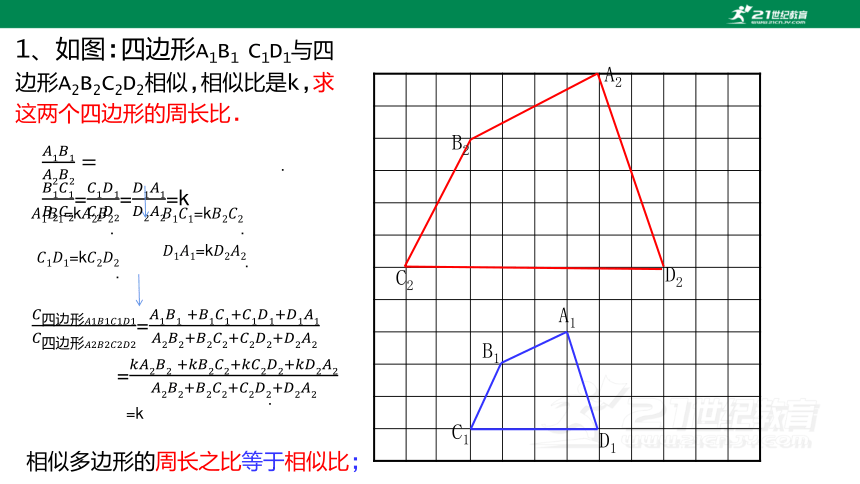
1、如图:四边形A1B1 C1D1与四边形A2B2C2D2相似,相似比是k,求这两个四边形的周长比.
A2
B2
C2
D2
A1
B1
C1
D1
===k
.
=k
.
=k
.
=k
.
=k
.
=
.
.
=
.
=k
相似多边形的周长之比等于相似比;
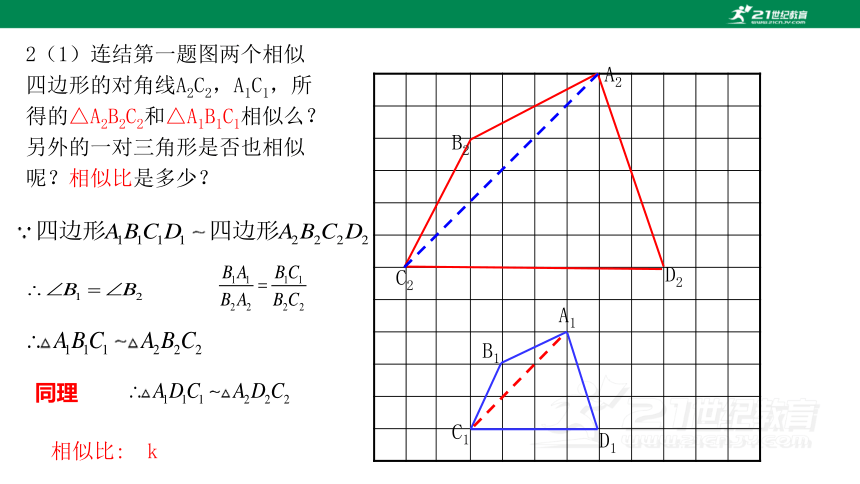
2(1)连结第一题图两个相似四边形的对角线A2C2,A1C1,所得的△A2B2C2和△A1B1C1相似么?另外的一对三角形是否也相似呢?相似比是多少?
A2
B2
C2
D2
A1
B1
C1
D1
同理
相似比: k
同理
A2
B2
C2
D2
A1
B1
C1
D1
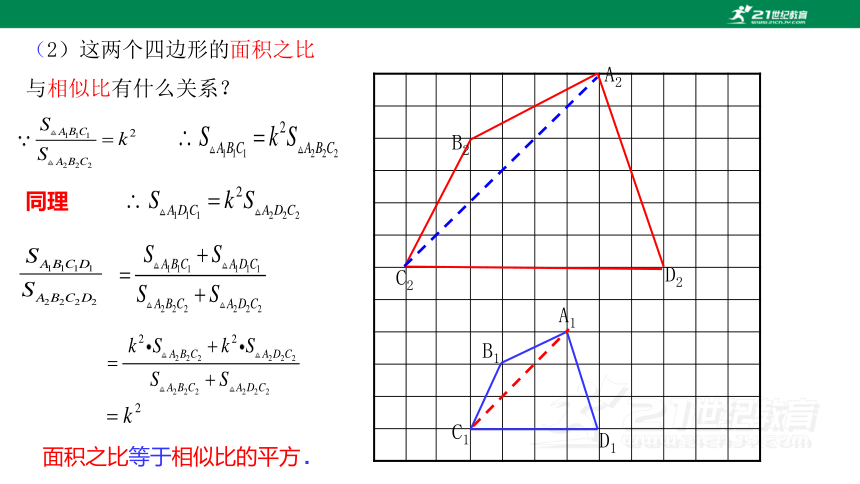
(2)这两个四边形的面积之比
与相似比有什么关系?
面积之比等于相似比的平方.
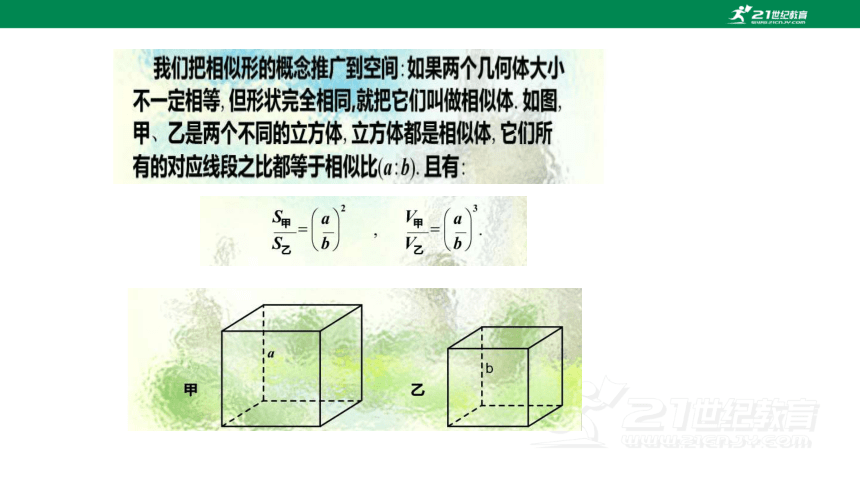
生活中我们会碰到许多这样形状相同,大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
【提问1】全等图形和相似图形有什么关系呢?
相似图形
全等形
全等图形是相似图形的一种特殊形式
【提问2】如果两个图形相似,这两个图形有什么关系呢?
两个图形相似,其中一个图形可以看作由另一个图形_____________得到.
放大或缩小
解:两张矩形纸张相似,理由如下:
矩形纸张的长与宽的比为 ,对开后所得的矩形纸张是否与原来的矩形纸相似 请说明理由.
A
B
C
D
E
F
设原来的纸张为矩形ABCD,
对折线EF把矩形ABCD分为两个全等的矩形.
在矩形ABFE中
∴矩形ABFE与矩形BCDA相似.
∴两个矩形的对应角相等,对应边成比例
.
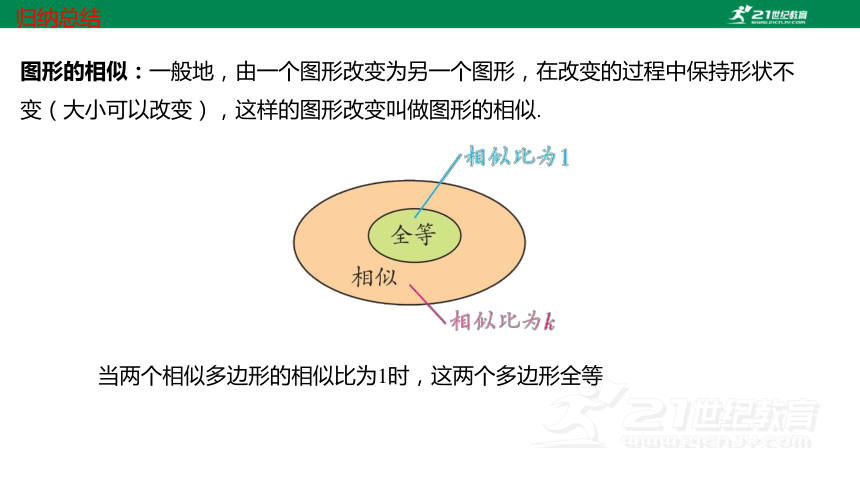
图形的相似:一般地,由一个图形改变为另一个图形,在改变的过程中保持形状不变(大小可以改变),这样的图形改变叫做图形的相似.
当两个相似多边形的相似比为1时,这两个多边形全等
归纳总结
1.在如图所示的相似四边形中,求未知的边长x和角度α的大小.
x=2.5
α=3600-1200-1250-550=60°
夯实基础,稳扎稳打
正方形
10
10
菱形
12
12
正方形
10
10
矩形
12
8
它们相似吗?
它们呢?
注意:两个多边形相似必须同时具有两个条件
2.
各对应边成比例
各对应角相等
(1)对应角都相等的两个多边形不一定相似,如矩形;
(2)对应边成比例的两个多边形不一定相似,如菱形;
(3)边数相同的正多边形都相似,如正方形,正五边形等.
注意:两个多边形相似必须同时具有两个条件
各对应边成比例+
各对应角相等
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
如图,五边形ABCDE∽五边形ABCDE ,它们的角和边有什么关系?
.
.
∠A=∠A, ∠B=∠B, ∠C=∠C, ∠D=∠D, ∠E=∠E
.
= = = =
.
3. 如图,在长为8cm,宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】
设留下矩形的宽为xcm,
∵留下的矩形(图中阴影部分)与原矩形相似,
∴,解得
则留下矩形的面积为 .故选C.
.
4.如图,在四边形ABCD中,B′,C′,D′分别是AB,AC,AD上的点,B′C′∥BC,C′D′∥CD.判断四边形ABCD与四边形A′B′C′D′是否相似,并说明理由.
相似,理由如下:由B′C′∥BC,得
△AB′C′∽△ABC,可得,
∠A′B′C′=∠B,∠AC′B′=∠ACB.
同理,由C′D′∥CD,可△AC′D′∽△ACD,
可得 ,∠AC′D′=∠ACD,
∠AD′C′=∠D.
所以在四边形A′B′C′D和四边形ABCD中
,
∠AB′C′=∠B,
∠B′C′D′=∠AC′B′+∠AC′D′
=∠ACB+∠ACD =∠BCD,
∠AD′C′=∠D,∠BAD是公共角,
即对应边成比例,对应角相等,故四边形ABCD与四边形A′B′C′D′相似.
连续递推,豁然开朗
点E,F分别是AB,AD的中点时,四边形AEGF的面积是四边形ABCD面积的
5.如图,四边形AEGF∽四边形ABCD,点E,F分别在AB,AD上.当点E,F
满足什么条件时,四边形AEGF的面积是四边形ABCD的面积的
6. 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所构成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
解:由题意得,EF=10 ,EH=20,AB=12,AD=22
∴小路内外边缘所构成的矩形EFGH和矩形ABCD不相似
.
7. 把一个长方形(如图)划分成三个全等的长方形.
若要使每一个小长方形与原长方形相似,则原长方形应满足什么条件
解: 由题意得
∵矩形ABFE与矩形BCDA相似
长方形纸张的长与宽的比为 满足要求.
8.
思维拓展,更上一层
9.把标准纸(长与宽之比为 )一次又一次对开如右图叠起来,
你发现了什么有趣的现象?你能给出数学解释吗?
.
x
y
0
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
4.6 相似多边形
第四章 相似三角形
观察下面的图形有什么特点?
相同点: 形状相同
不同点: 大小不一定相同
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
温故知新
1、如图:四边形A1B1 C1D1与四边形A2B2C2D2相似,相似比是k,求这两个四边形的周长比.
A2
B2
C2
D2
A1
B1
C1
D1
===k
.
=k
.
=k
.
=k
.
=k
.
=
.
.
=
.
=k
相似多边形的周长之比等于相似比;
2(1)连结第一题图两个相似四边形的对角线A2C2,A1C1,所得的△A2B2C2和△A1B1C1相似么?另外的一对三角形是否也相似呢?相似比是多少?
A2
B2
C2
D2
A1
B1
C1
D1
同理
相似比: k
同理
A2
B2
C2
D2
A1
B1
C1
D1
(2)这两个四边形的面积之比
与相似比有什么关系?
面积之比等于相似比的平方.
生活中我们会碰到许多这样形状相同,大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为相似形.
【提问1】全等图形和相似图形有什么关系呢?
相似图形
全等形
全等图形是相似图形的一种特殊形式
【提问2】如果两个图形相似,这两个图形有什么关系呢?
两个图形相似,其中一个图形可以看作由另一个图形_____________得到.
放大或缩小
解:两张矩形纸张相似,理由如下:
矩形纸张的长与宽的比为 ,对开后所得的矩形纸张是否与原来的矩形纸相似 请说明理由.
A
B
C
D
E
F
设原来的纸张为矩形ABCD,
对折线EF把矩形ABCD分为两个全等的矩形.
在矩形ABFE中
∴矩形ABFE与矩形BCDA相似.
∴两个矩形的对应角相等,对应边成比例
.
图形的相似:一般地,由一个图形改变为另一个图形,在改变的过程中保持形状不变(大小可以改变),这样的图形改变叫做图形的相似.
当两个相似多边形的相似比为1时,这两个多边形全等
归纳总结
1.在如图所示的相似四边形中,求未知的边长x和角度α的大小.
x=2.5
α=3600-1200-1250-550=60°
夯实基础,稳扎稳打
正方形
10
10
菱形
12
12
正方形
10
10
矩形
12
8
它们相似吗?
它们呢?
注意:两个多边形相似必须同时具有两个条件
2.
各对应边成比例
各对应角相等
(1)对应角都相等的两个多边形不一定相似,如矩形;
(2)对应边成比例的两个多边形不一定相似,如菱形;
(3)边数相同的正多边形都相似,如正方形,正五边形等.
注意:两个多边形相似必须同时具有两个条件
各对应边成比例+
各对应角相等
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
如图,五边形ABCDE∽五边形ABCDE ,它们的角和边有什么关系?
.
.
∠A=∠A, ∠B=∠B, ∠C=∠C, ∠D=∠D, ∠E=∠E
.
= = = =
.
3. 如图,在长为8cm,宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】
设留下矩形的宽为xcm,
∵留下的矩形(图中阴影部分)与原矩形相似,
∴,解得
则留下矩形的面积为 .故选C.
.
4.如图,在四边形ABCD中,B′,C′,D′分别是AB,AC,AD上的点,B′C′∥BC,C′D′∥CD.判断四边形ABCD与四边形A′B′C′D′是否相似,并说明理由.
相似,理由如下:由B′C′∥BC,得
△AB′C′∽△ABC,可得,
∠A′B′C′=∠B,∠AC′B′=∠ACB.
同理,由C′D′∥CD,可△AC′D′∽△ACD,
可得 ,∠AC′D′=∠ACD,
∠AD′C′=∠D.
所以在四边形A′B′C′D和四边形ABCD中
,
∠AB′C′=∠B,
∠B′C′D′=∠AC′B′+∠AC′D′
=∠ACB+∠ACD =∠BCD,
∠AD′C′=∠D,∠BAD是公共角,
即对应边成比例,对应角相等,故四边形ABCD与四边形A′B′C′D′相似.
连续递推,豁然开朗
点E,F分别是AB,AD的中点时,四边形AEGF的面积是四边形ABCD面积的
5.如图,四边形AEGF∽四边形ABCD,点E,F分别在AB,AD上.当点E,F
满足什么条件时,四边形AEGF的面积是四边形ABCD的面积的
6. 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所构成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
解:由题意得,EF=10 ,EH=20,AB=12,AD=22
∴小路内外边缘所构成的矩形EFGH和矩形ABCD不相似
.
7. 把一个长方形(如图)划分成三个全等的长方形.
若要使每一个小长方形与原长方形相似,则原长方形应满足什么条件
解: 由题意得
∵矩形ABFE与矩形BCDA相似
长方形纸张的长与宽的比为 满足要求.
8.
思维拓展,更上一层
9.把标准纸(长与宽之比为 )一次又一次对开如右图叠起来,
你发现了什么有趣的现象?你能给出数学解释吗?
.
x
y
0
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
