2。1一元二次方程(1)(浙江省温州市)
文档属性
| 名称 | 2。1一元二次方程(1)(浙江省温州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 560.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-05 00:00:00 | ||
图片预览






文档简介
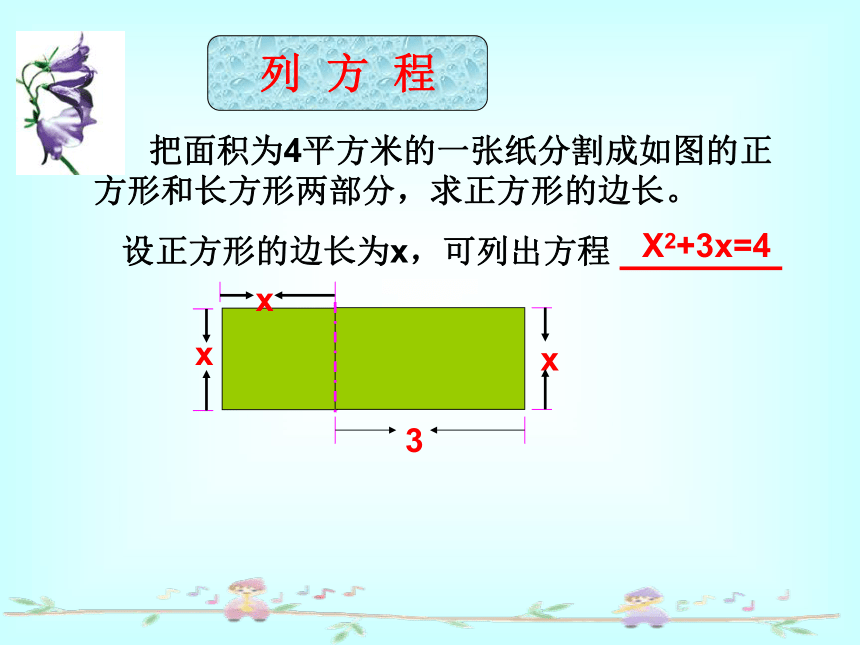
课件22张PPT。2.1一元二次方程列 方 程 把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
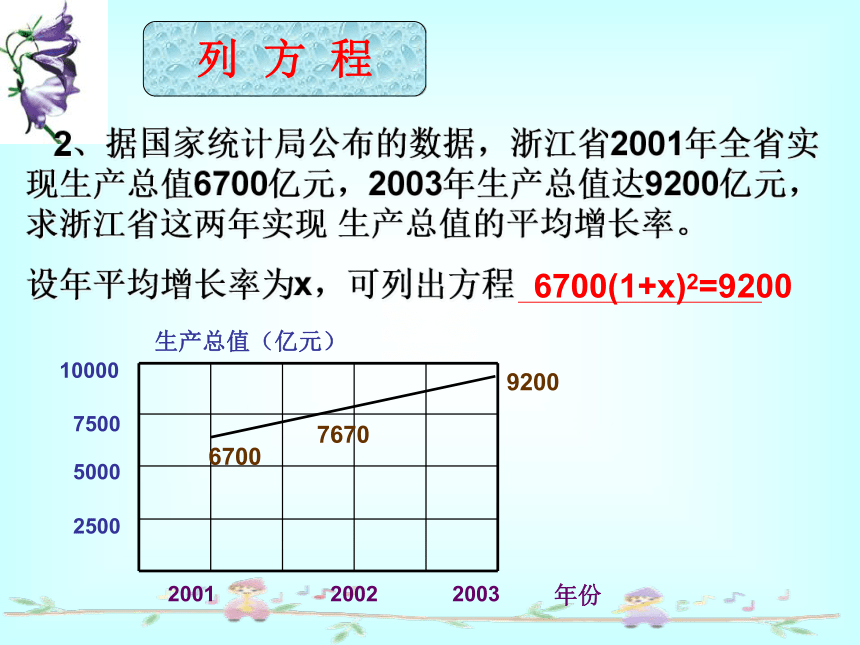
设正方形的边长为x,可列出方程 xX2+3x=4 2、据国家统计局公布的数据,浙江省2001年全省实现生产总值6700亿元,2003年生产总值达9200亿元,求浙江省这两年实现 生产总值的平均增长率。
设年平均增长率为x,可列出方程6700(1+x)2=920025005000750010000200120022003年份生产总值(亿元)920076706700列 方 程观察所列方程,说出这些方程与一元一次方程的相同和不同之处。
x2+3x=4; 6700(1+x)2=9200,
一元二次方程:
两边都是整式,只含有一个未知数,并且未知数的最高次数是2次。2.1一元二次方程一元二次方程①方程两边都是整式②只含有一个未知数③未知数的最高次数是2次 能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).1、判断下列方程是否为一元二次方程:① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
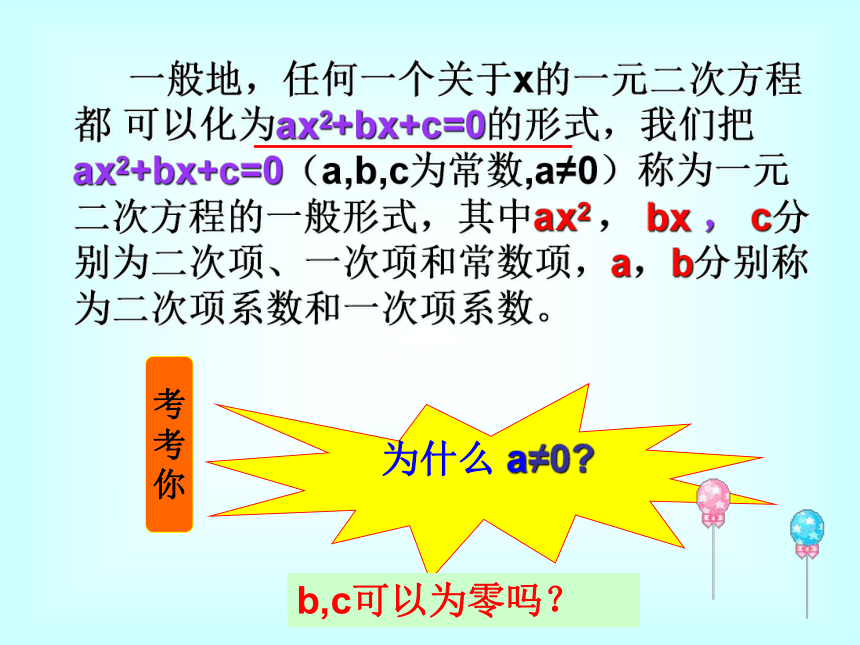
⑦4x2=5x ( ) ⑧3y2+4=5y ( ) 是是是是不是不是不是是2、判断未知数的值 x=-1,x=0,x=2是不是方程x2-2=x的根。 一般地,任何一个关于x的一元二次方程都 可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2 , bx , c分别为二次项、一次项和常数项,a,b分别称为二次项系数和一次项系数。考
考
你为什么 a≠0?
b,c可以为零吗?例1:把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.注意:
在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。一元二次方程的一般形式:ax2+bx+c=0(a≠0)课内练习1、在下列方程中,是一元二次方程的为( )
(A)x2+3x= (B)2(x-1)+x=2.
(C)x2=2+3x (D)x2-x3+4=0.2
XC 2、把一元二次方程(x-√5 )(x+√5 )+(2x-1)2=0化为一般形式,正确的是( )A、5x2-4x-4=0B、x2-5=0C、5x2-2x+1=0D、5x2-4x+6=0A3、填空:X2-4x-3=01 -4 -3 0.5 0 -4 0 3x2-2x-1=03 -2 -1 4、已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值。5、已知关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根是1, 求a+b+c的值。若a-b+c=0,你能通过观察,求出一元二次方程ax2+bx+c=0的一个根吗?6、一个长为10m的梯子斜靠在墙上,梯子的顶端距离地面的垂直距离为8m, 如果梯子的顶端下滑1m,那么梯子的底端滑动多少m?由勾股定理可知,滑动前梯子底端距墙 m,6如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m. (x+6)根据题意,可得方程(x+6)2+72=102请你把它化成一般形式6(x+6)7、这是温州市区某条大道上的一个长方形花坛,它的长为___米,宽为___米,现要求在四周种上宽度相等的红花作为花边,花坛中央黄、白两种花的长方形种植面积为18平方米,问______________?
(花坛四周的边沿建筑面积不计) 请在上面的句子中设计所要求的问题,使它能够通过列一元二次方程来解决。85花边有多宽布置作业作业纸
课本作业题(1~4做书上)
教学练2.1探索与交流 请找出符合下列要求的一元二次方程:(1)含有未知数x;
(2)方程有一个根是2. 比比谁找得多,形式又丰富.并与同学交流你的方法.欣赏民谣一群猴子分两队,高高兴兴在游戏。
八分之一再平方,蹦蹦跳跳树林里。
其余十二高声喊,充分活跃的空气,
告我总数共多少,两队猴子在一起? 请把民谣里所蕴涵的数学问题用方程表示出来(不用求解)。 1(印度)
牧童王小良,放牧一群羊。
问他羊几只,请你仔细想。
头数加只数,只数减头数。
只数乘头数,只数除头数。
四数连加起,正好一百数。
2(中国)2、填表:
提高与延伸 某百货商店服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接“六·一”国际儿童节,商场决定采取适当的降价措施,如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元? (1)如果设每件童装应降价x元,则可以列出怎样的方程?(2)方程列出后,你会解吗?拓展加深已知关于x的一元二次方程有一个根是0,求m的值.
设正方形的边长为x,可列出方程 xX2+3x=4 2、据国家统计局公布的数据,浙江省2001年全省实现生产总值6700亿元,2003年生产总值达9200亿元,求浙江省这两年实现 生产总值的平均增长率。
设年平均增长率为x,可列出方程6700(1+x)2=920025005000750010000200120022003年份生产总值(亿元)920076706700列 方 程观察所列方程,说出这些方程与一元一次方程的相同和不同之处。
x2+3x=4; 6700(1+x)2=9200,
一元二次方程:
两边都是整式,只含有一个未知数,并且未知数的最高次数是2次。2.1一元二次方程一元二次方程①方程两边都是整式②只含有一个未知数③未知数的最高次数是2次 能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).1、判断下列方程是否为一元二次方程:① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5x ( ) ⑧3y2+4=5y ( ) 是是是是不是不是不是是2、判断未知数的值 x=-1,x=0,x=2是不是方程x2-2=x的根。 一般地,任何一个关于x的一元二次方程都 可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2 , bx , c分别为二次项、一次项和常数项,a,b分别称为二次项系数和一次项系数。考
考
你为什么 a≠0?
b,c可以为零吗?例1:把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.注意:
在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。一元二次方程的一般形式:ax2+bx+c=0(a≠0)课内练习1、在下列方程中,是一元二次方程的为( )
(A)x2+3x= (B)2(x-1)+x=2.
(C)x2=2+3x (D)x2-x3+4=0.2
XC 2、把一元二次方程(x-√5 )(x+√5 )+(2x-1)2=0化为一般形式,正确的是( )A、5x2-4x-4=0B、x2-5=0C、5x2-2x+1=0D、5x2-4x+6=0A3、填空:X2-4x-3=01 -4 -3 0.5 0 -4 0 3x2-2x-1=03 -2 -1 4、已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值。5、已知关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根是1, 求a+b+c的值。若a-b+c=0,你能通过观察,求出一元二次方程ax2+bx+c=0的一个根吗?6、一个长为10m的梯子斜靠在墙上,梯子的顶端距离地面的垂直距离为8m, 如果梯子的顶端下滑1m,那么梯子的底端滑动多少m?由勾股定理可知,滑动前梯子底端距墙 m,6如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m. (x+6)根据题意,可得方程(x+6)2+72=102请你把它化成一般形式6(x+6)7、这是温州市区某条大道上的一个长方形花坛,它的长为___米,宽为___米,现要求在四周种上宽度相等的红花作为花边,花坛中央黄、白两种花的长方形种植面积为18平方米,问______________?
(花坛四周的边沿建筑面积不计) 请在上面的句子中设计所要求的问题,使它能够通过列一元二次方程来解决。85花边有多宽布置作业作业纸
课本作业题(1~4做书上)
教学练2.1探索与交流 请找出符合下列要求的一元二次方程:(1)含有未知数x;
(2)方程有一个根是2. 比比谁找得多,形式又丰富.并与同学交流你的方法.欣赏民谣一群猴子分两队,高高兴兴在游戏。
八分之一再平方,蹦蹦跳跳树林里。
其余十二高声喊,充分活跃的空气,
告我总数共多少,两队猴子在一起? 请把民谣里所蕴涵的数学问题用方程表示出来(不用求解)。 1(印度)
牧童王小良,放牧一群羊。
问他羊几只,请你仔细想。
头数加只数,只数减头数。
只数乘头数,只数除头数。
四数连加起,正好一百数。
2(中国)2、填表:
提高与延伸 某百货商店服装柜在销售中发现:“宝乐”牌童装平均每天可售出20件,每件盈利40元,为了迎接“六·一”国际儿童节,商场决定采取适当的降价措施,如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天在销售这种童装上盈利1200元,那么每件童装应降价多少元? (1)如果设每件童装应降价x元,则可以列出怎样的方程?(2)方程列出后,你会解吗?拓展加深已知关于x的一元二次方程有一个根是0,求m的值.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
