【浙教版】数学2014-2015学年八年级下册“单元精品卷”第五章 特殊平行四边形(卷1)
文档属性
| 名称 | 【浙教版】数学2014-2015学年八年级下册“单元精品卷”第五章 特殊平行四边形(卷1) |  | |
| 格式 | zip | ||
| 文件大小 | 413.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-23 08:59:47 | ||
图片预览


文档简介
【浙教版】数学2014-2015学年八年级下册“单元精品卷”(卷1)
第五章 特殊平行四边形
题号
仔细选一选
认真填一填
全面答一答
总 分
得分
一、仔细选一选。(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内.注意可以用多种不同的方法来选取正确答案.
1.如图,把一长方形纸片ABCD沿EG折叠后,点A、B分别落在A′、B′的位置上,EA′与BC相交于点F,已知∠1=130°,则∠2的度数是( )【来源:21·世纪·教育·网】
A.40° B.50° C.65° D.80°
2.下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互 相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
3.下列图形都是由同样大小的矩形按一定规律组成,其中第(1)个图形的面积为2,第(2)个图形的面积为8,第(3)个图形的面积为18,……,则第(10)个图形的面积为( )21·世纪*教育网
A.196 B.200 C. 216 D.256
4.顺次连结一个四边形各边中点所得的四边形必定是( )
A、平行四边形 B、矩形 C、菱形 D、正方形.
5.如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分别是AB,BC的中点,则下列结论不一定正确的是( )2-1-c-n-j-y
A.△ABC是等腰三角形
B.四边形EFAM是菱形
C.S△BEF=S△ACD
D.DE平分∠CDF
6.矩形具有而菱形不一定具有的性质是( )
A.两组对边分别平行
B.对角线相等
C.对角线互相平分
D.两组对角分别相等
7.如图,在正方形ABCD中,F为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,那么∠EFD的度数为( )
A.10° B.15° C.20° D.25°
8.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为( ) 21*cnjy*com
A.(﹣,1) B.(﹣1,)
C.(,1) D.(﹣,﹣1)
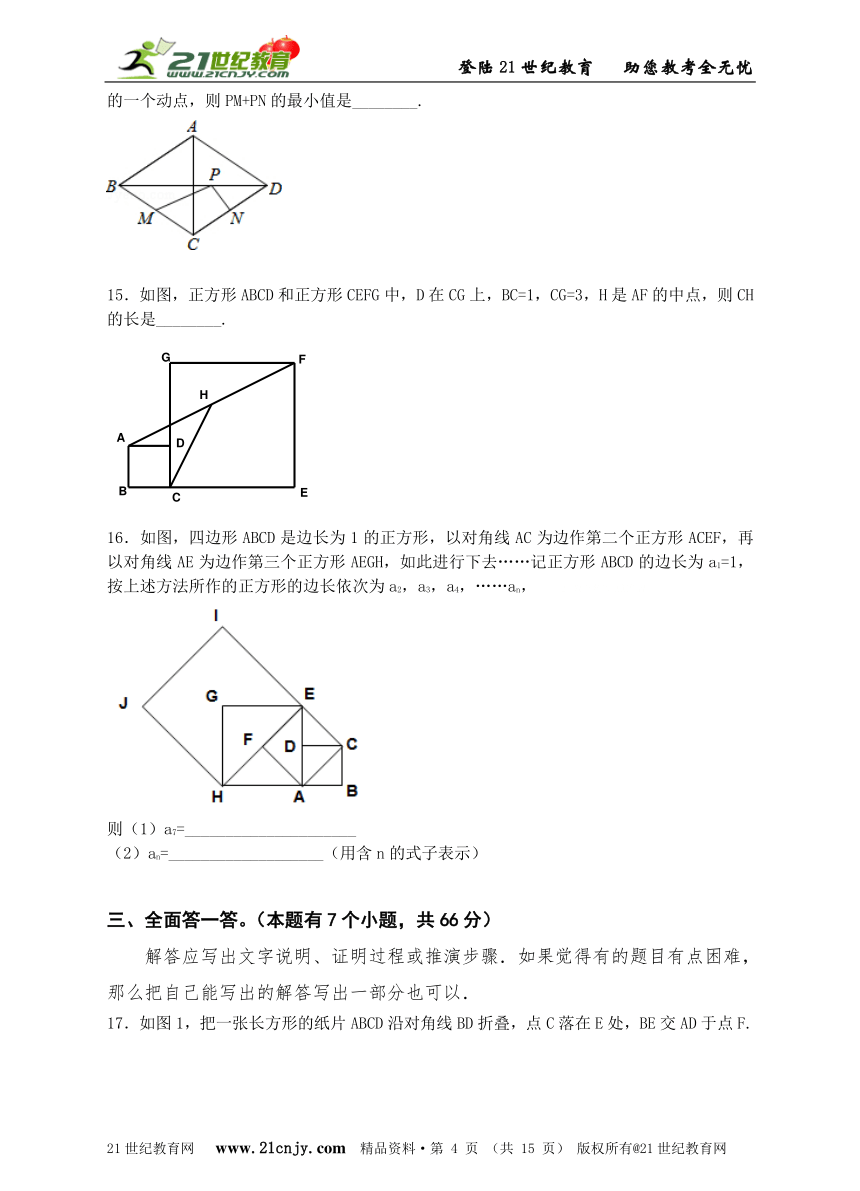
9.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )【来源:21cnj*y.co*m】
A. B. C.2 D.1
10.将一个正方形纸片依次按图1a,b的方式对折,然后沿图c中的虚线裁剪,成图d样式,将纸展开铺平,所得到的图形是图中的 ( )【版权所有:21教育】
图1
二、认真填一填。(本题有6个小题,每小题4分,共24分)
要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.
11.如图,矩形ABCD的周长是20,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正
方形ABEF和ADGH的面积之和为68,那么矩形ABCD的面积是________.
12.广告公司为某种商品设计了一种商标图案(如图所示),图中阴影部分为红色.若每个小长方形的面积都是1,则红色部分的面积是________.
13.菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形AB的周长为________.
14.如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是________.
15.如图,正方形ABCD和正方形CEFG中,D在CG上,BC=1,CG=3,H是AF的中点,则CH的长是________.
16.如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此进行下去……记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,……an, 21教育名师原创作品
则(1)a7=_____________________
(2)an=___________________(用含n的式子表示)
三、全面答一答。(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.
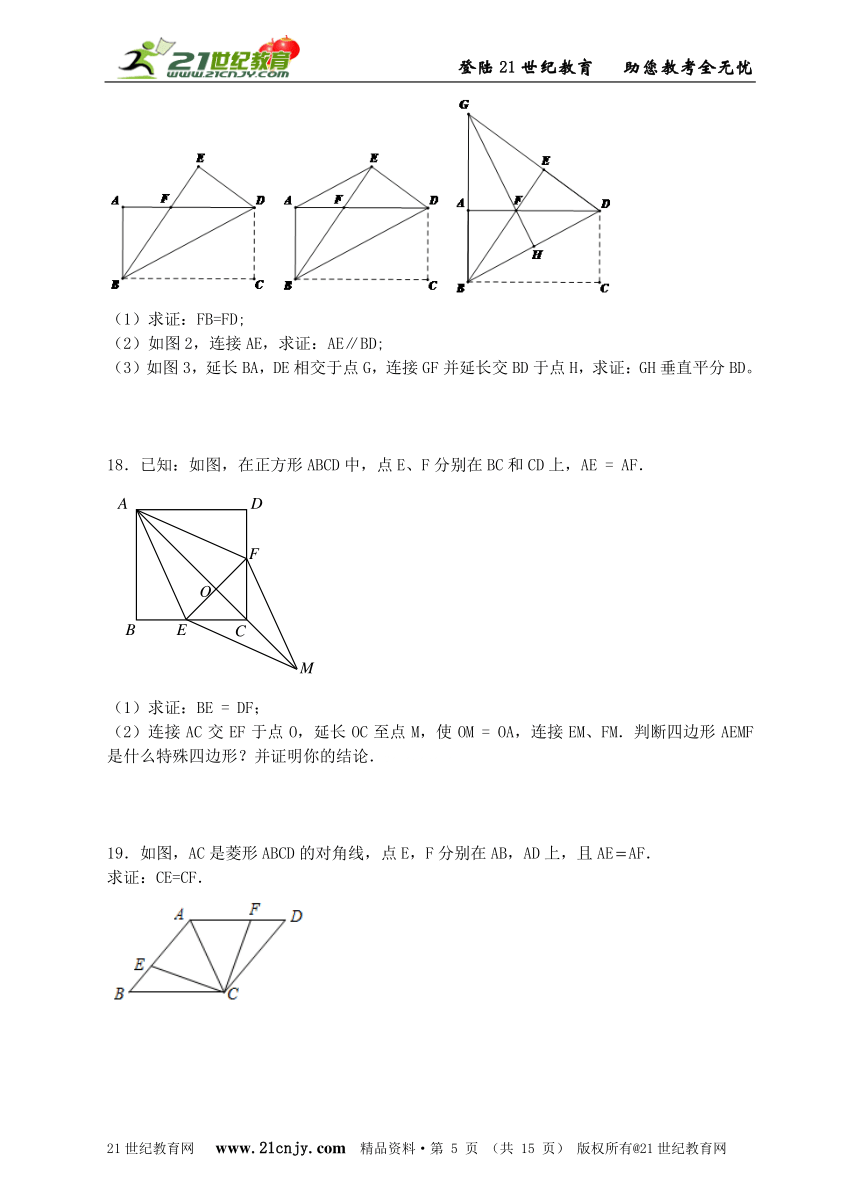
17.如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD。
18.已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.2·1·c·n·j·y
19.如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AEAF.
求证:CE=CF.
20.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
(1)求证:四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.
21.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
22.已知,如图,正方形ABCD,菱形EFGP,点E、F、G分别在AB、AD、CD上,延长DC,PHDC于H。
(1)求证:GH=AE
(2)若菱形的周长为20cm,求的面积
23.正方形ABCD中,将一个直角三角板的直角顶点与点A重合,一条直角边与边BC交于点E(点E不与点B和点C重合),另一条直角边与边CD的延长线交于点F.
(1)如图①,求证:AE=AF;
(2)如图②,此直角三角板有一个角是45°,它的斜边MN与边CD交于G,且点G是斜边MN的中点,连接EG,求证:EG=BE+DG;
(3)在(2)的条件下,如果= ,那么点G是否一定是边CD的中点?请说明你的理由.
参考答案与详解
1.D.
2.C.
【解析】A、对角线相等的平行四边形是矩形,所以A选项错误;
B、对角线互相垂直的平行四边形是菱形,所以B选项错误;
C、对角线互相垂直平分且相等的四边形是正方形,所以C选项正确;
D、一组对边相等且平行的四边形是平行四边形,所以D选项错误.
故选C.
3.B.
【解析】∵第一个图形面积为:2=1×2(cm2),
第二个图形面积为:8=22×2(cm2),
第三个图形面积为:18=32×2(cm2)…
∴第10个图形的面积为:102×2=200(cm2).
故选B.
4.A.
【解析】 如图四边形ABCD,E、N、M、F分别是DA,AB,BC,DC中点,连接AC,DE,
根据三角形中位线定理可得:
EF平行且等于AC的一半,MN平行且等于AC的一半,
根据平行四边形的判定,可知四边形为平行四边形.
故选:A.
5.D.
【解析】连接AE,如图所示,
∵E为BC的中点,
∴BE=CE=BC,又BC=2AD,∴AD=BE=EC,又AD∥BC,
∴四边形ABED为平行四边形,四边形AECD为平行四边形,
又∵∠DCB=90°,∴四边形AECD为矩形,∴∠AEC=90°,即AE⊥BC,∴AE垂直平分BC,
∴AB=AC,即△ABC为等腰三角形,
故选项A不合题意;
∵E为BC的中点,F为AB的中点,∴EF为△ABC的中位线,∴EF∥AC,EF=AC,
又∵四边形ABED为平行四边形,∴AF∥ME,∴四边形AFEM为平行四边形,
又∵AF=AB=AC=EF,∴四边形AFEM为菱形,故选项B不合题意;
过F作FN⊥BC于N点,可得FN∥AE,
又∵F为AB的中点,∴N为BE的中点,∴FN为△ABE的中位线,∴FN=AE,
又∵AE=DC,BE=AD,∴S△BEF=S△ACD,故选项C不合题意;DE不一定平分∠CDF,
故选项D符合题意.
6.B
【解析】∵菱形与矩形都是平行四边形,A, C是平行四边形的性质,
∴二者都具有,故此两个选项都不正确,
由于菱形的对角线互相垂直且平分每一组对角,而矩形的对角线则相等,故选:B
7.B.
【解析】∵△BCE绕点C顺时针方向旋转90°得到△DCF,
∴CE=CF,∠DFC=∠BEC=60°,∠EFC=45°,∴∠EFD=60°-45°=15°.故选B.
8.A.
【解析】如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,∴∠OAD=∠COE,
在△AOD和△OCE中,
,∴△AOD≌△OCE(AAS),∴OE=AD=,CE=OD=1,
∵点C在第二象限,∴点C的坐标为(-,1).
9.B.
【解析】∵BD、GE分别是正方形ABCD,正方形CEFG的对角线,
∴∠ADB=∠CGE=45°,∴∠GDT=180°﹣90°﹣45°=45°,
∴∠DTG=180°﹣∠GDT﹣∠CGE=180°﹣45°﹣45°=90°,
∴△DGT是等腰直角三角形,
∵两正方形的边长分别为4,8,∴DG=8﹣4=4,∴GT=.故选B.
10.D.
【解析】严格按照图中的顺序向上对折,向右对折,从右下角剪去一个四分之一圆,从左上角和左下角各剪去一个直角三角形,展开得到结论.故选D.www.21-cn-jy.com
11.16
【解析】设AB=x,BC=y,根据题意得:,,所以,所以,即矩形ABCD的面积是16.
12.5
【解析】由题意知阴影面积等于矩形面积减去3个空白三角形的面积,设每个小长方形长为a,宽为b,则ab=1.即4a×4b-a×4b-×3a×3b-×3a×3b=16ab-2ab-9ab=5ab=5.
13.16
【解析】∵解方程x2-7x+12=0得:x=3或4
∵对角线长为6,3+3=6,不能构成三角形;∴菱形的边长为4.∴菱形ABCD的周长为4×4=16
14.5
【解析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,∴AC∥MQ,
∵M为BC中点,∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,∴BQ∥CD,BQ=CN,∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,即NQ=5,
∴MP+NP=QP+NP=QN=5,
15..
【解析】连接AC、CF,根据正方形性质求出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边上的中线等于斜边的一半解答即可.
解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,
∠ACD=∠GCF=45°,∴∠ACF=90°,
由勾股定理得,AF=,
∵H是AF的中点,∴CH=AF=.
16.()6, ()n-1.
【解析】根据第一个正方形的边长为1可以求得第二个正方形的边长,以此类推可以求得正方形的边长满足一定的规律,根据次规律可以求得第n个正方形的边长.
解:∵正方形ABCD的边长为1的正方形,
∴a1=1=()0,
∵AC是正方形ABCD的对角线,∴AC=,∴a2=,
同理可得
a3=
a4=,
…
a7=()6∴an=()n-1.
17.(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】(1)由折叠的性质可得到△ABD≌△EDB,那么∠ADB=∠EBD,所以BF=DF;
(2)根据长方形的性质可得和三角形内角和定理可得∠AEF=∠FBD,再根据平行线的判定即可求解;
(3)先SSS证明△ABD≌△EDB,再根据全等三角形的性质和垂直平分线的性质即可求解.
解:(1)∵△BCD≌△BED,∴∠DBC=∠EBD,
又∵四边形ABCD是长方形,∴AD∥BC,∴∠ADB=∠DBC,∴∠ADB=∠EBD,∴BF=DF.
(2)∵四边形ABCD是长方形,∴AD=BC=BE,
又∵FB=FD,∴FA=FE,∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF+∠AFE=2∠FBD+∠BFD=180°,
∴∠AEF=∠FBD,∴AE∥BD;
(3)∵四边形ABCD是长方形,∴AD=BC=BE,AB=CD=DE,BD=DB,
在△ABD与△EDB中,
∴△ABD≌△EDB(SSS),∴∠ABD=∠EDB,∴GB=GD,
又∵FB=FD,∴GF是BD的垂直平分线,即GH垂直平分BD.
18.(1)见解析(5分)(2)菱形 证明:见解析(5分)
【解析】(1)根据条件证△ABE≌△ADF即可;(2)因为OA=OM,所以证明EF、AM互相垂直平分,从而可判定四边形AEMF是菱形.21·cn·jy·com
解:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,在Rt△ABE和Rt△ADF中,∵AD=AB,AF=AE,∴Rt△ADF≌Rt△ABE(HL)∴BE=DF;(2)解:四边形AEMF是菱形,理由为:证明:∵四边形ABCD是正方形,∴∠BCA=∠DCA=45°,BC=DC,∵BE=DF,∴BC-BE=DC-DF,即CE=CF,在△COE和△COF中CE=CF,∠ACB=∠ACD, OC=OC∴△COE≌△COF(SAS),∴OE=OF,又OM=OA,∴四边形AEMF是平行四边形,∵AE=AF,∴平行四边形AEMF是菱形.www-2-1-cnjy-com
19.见解析
【解析】由菱形的性质得到从而的证.
解:∵ 四边形ABCD是菱形∴
又∵AE=AF,AC为公共边∴∴CE=CF 、
20.(1)证明见试题解析;(2)∠B=30°,证明见试题解析.
【解析】(1)易证∠DEC=∠DFA,即可得CE∥AF,根据CE=AF可得四边形ACEF为平行四边形;【出处:21教育名师】
(2)要使得平行四边形ACEF为菱形,则AC=CE,又∵CE=AB,∴使得AB=2AC即可,根据AB、AC即可求得∠B的值.21*cnjy*com
解:(1)∵DE为BC的垂直平分线,∴∠EDB=90°,BD=DC,
又∵∠ACB=90°,∴DE∥AC,∴E为AB的中点,∴在Rt△ABC中,CE=AE=BE,
∴∠AEF=∠AFE,且∠BED=∠AEF,∴∠DEC=∠DFA,∴AF∥CE,
又∵AF=CE,∴四边形ACEF为平行四边形;
(2)要使得平行四边形ACEF为菱形,则AC=CE即可,
∵DE∥AC,∴∠BED=∠BAC,∠DEC=∠ECA,
又∵∠BED=∠DEC,∴∠EAC=∠ECA,∴AE=EC,又EB=EC,∴AE=EC=EB,
∵CE=AB,∴AC=AB即可,
在Rt△ABC中,∠ACB=90°,∴当∠B=30°时,AB=2AC,
故∠B=30°时,四边形ACEF为菱形.
21.(1)AE=CF (2)∠EGC=80°
【解析】(1)要证AE=CF,若我们能够证明其所在的三角形全等即可。AE位于
△AEB中,CF位于△CFB中,因为四边形ABCD是正方形,则AB=BC,因为
BE⊥BF,则∠ABC=∠EBF=90°,都减去∠EBC,故∠ABE=∠CBF,又因为BE=BF,故可以
由SAS定理得到两个三角形全等。故AE=CF。
(2)由三角形的外角等于和他不相邻的两个内角之和,则∠EGC=∠EBG+∠BEF,由BE⊥BF,
∠FBE=90°,BE=BF,则∠BEF=∠EFB=45°,而∠EBG=90°-∠ABE=90°-55°=35°,故可求出∠EGC=80°。21教育网
解:
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵BE⊥BF,
∴∠FBE=90°,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF,
在△AEB和△CFB中,
∴△AEB≌△CFB(SAS),
∴AE=CF. .
(2)解:∵BE⊥BF,
∴∠FBE=90°,
又∵BE=BF,
∴∠BEF=∠EFB=45°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
又∵∠ABE=55°,
∴∠EBG=90°-55°=35°,
∴∠EGC=∠EBG+∠BEF=45°+35°=80°
22.(1)详见解析 (2)
【解析】
①连接EG,∵AB∥DH,∴∠AEG=∠EGC。∵EF∥GP,∴∠FEG=∠EGP,∴∠AEF=∠PGC,有∵EF=PG,∠A=∠H=,∴ΔAEF≌ΔPGH,∴GH=AE21世纪教育网版权所有
②∵EF=5,cos∠AFE==,∴AF=4,AE=3。∵FD=2,∴AD=DC=6。∵
∴,∵PH=AF=4,∴
23.
【解析】(1)根据正方形的性质得出∠ABC=∠ADF=90°,进而得出△ABE≌△ADF,即可得出AE=AF;21cnjy.com
(2)连接AG,利用全等三角形的判定得出△AEG≌△AFG(SAS),进而得出EG=BE+DG;
(3)首先设AB=5k,GF=6k,再假设BE=x,则CE=6k-x,EG=5k,得出CF=CD+DF=6k+x,CG=CF-GF=6k+x-5k=k+x,进而利用勾股定理得出x的值,进而比较得出答案.
解:(1)正方形ABCD中,AB=AD,
∠ABC=∠ADC=∠BAD= 90°
∴∠ABC=∠ADF=90°,
∵∠EAF=90°∴∠BAE=∠DAF
∴≌,
∴AE=AF
(2)连接AG,
∵点G是斜边MN的中点,
∴∠EAG=∠FAG=45°
AG=AG,则≌
∴EG=GF
∴EG=DG+DF
∵BE=DF
∴EG=BE+DG
第五章 特殊平行四边形
题号
仔细选一选
认真填一填
全面答一答
总 分
得分
一、仔细选一选。(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内.注意可以用多种不同的方法来选取正确答案.
1.如图,把一长方形纸片ABCD沿EG折叠后,点A、B分别落在A′、B′的位置上,EA′与BC相交于点F,已知∠1=130°,则∠2的度数是( )【来源:21·世纪·教育·网】
A.40° B.50° C.65° D.80°
2.下列命题中正确的是( )
A.对角线相等的四边形是矩形
B.对角线互 相垂直的四边形是菱形
C.对角线互相垂直平分且相等的四边形是正方形
D.一组对边相等,另一组对边平行的四边形是平行四边形
3.下列图形都是由同样大小的矩形按一定规律组成,其中第(1)个图形的面积为2,第(2)个图形的面积为8,第(3)个图形的面积为18,……,则第(10)个图形的面积为( )21·世纪*教育网
A.196 B.200 C. 216 D.256
4.顺次连结一个四边形各边中点所得的四边形必定是( )
A、平行四边形 B、矩形 C、菱形 D、正方形.
5.如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分别是AB,BC的中点,则下列结论不一定正确的是( )2-1-c-n-j-y
A.△ABC是等腰三角形
B.四边形EFAM是菱形
C.S△BEF=S△ACD
D.DE平分∠CDF
6.矩形具有而菱形不一定具有的性质是( )
A.两组对边分别平行
B.对角线相等
C.对角线互相平分
D.两组对角分别相等
7.如图,在正方形ABCD中,F为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,那么∠EFD的度数为( )
A.10° B.15° C.20° D.25°
8.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为( ) 21*cnjy*com
A.(﹣,1) B.(﹣1,)
C.(,1) D.(﹣,﹣1)
9.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )【来源:21cnj*y.co*m】
A. B. C.2 D.1
10.将一个正方形纸片依次按图1a,b的方式对折,然后沿图c中的虚线裁剪,成图d样式,将纸展开铺平,所得到的图形是图中的 ( )【版权所有:21教育】
图1
二、认真填一填。(本题有6个小题,每小题4分,共24分)
要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.
11.如图,矩形ABCD的周长是20,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正
方形ABEF和ADGH的面积之和为68,那么矩形ABCD的面积是________.
12.广告公司为某种商品设计了一种商标图案(如图所示),图中阴影部分为红色.若每个小长方形的面积都是1,则红色部分的面积是________.
13.菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形AB的周长为________.
14.如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是________.
15.如图,正方形ABCD和正方形CEFG中,D在CG上,BC=1,CG=3,H是AF的中点,则CH的长是________.
16.如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此进行下去……记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,……an, 21教育名师原创作品
则(1)a7=_____________________
(2)an=___________________(用含n的式子表示)
三、全面答一答。(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.
17.如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD。
18.已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.2·1·c·n·j·y
19.如图,AC是菱形ABCD的对角线,点E,F分别在AB,AD上,且AEAF.
求证:CE=CF.
20.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
(1)求证:四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.
21.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
22.已知,如图,正方形ABCD,菱形EFGP,点E、F、G分别在AB、AD、CD上,延长DC,PHDC于H。
(1)求证:GH=AE
(2)若菱形的周长为20cm,求的面积
23.正方形ABCD中,将一个直角三角板的直角顶点与点A重合,一条直角边与边BC交于点E(点E不与点B和点C重合),另一条直角边与边CD的延长线交于点F.
(1)如图①,求证:AE=AF;
(2)如图②,此直角三角板有一个角是45°,它的斜边MN与边CD交于G,且点G是斜边MN的中点,连接EG,求证:EG=BE+DG;
(3)在(2)的条件下,如果= ,那么点G是否一定是边CD的中点?请说明你的理由.
参考答案与详解
1.D.
2.C.
【解析】A、对角线相等的平行四边形是矩形,所以A选项错误;
B、对角线互相垂直的平行四边形是菱形,所以B选项错误;
C、对角线互相垂直平分且相等的四边形是正方形,所以C选项正确;
D、一组对边相等且平行的四边形是平行四边形,所以D选项错误.
故选C.
3.B.
【解析】∵第一个图形面积为:2=1×2(cm2),
第二个图形面积为:8=22×2(cm2),
第三个图形面积为:18=32×2(cm2)…
∴第10个图形的面积为:102×2=200(cm2).
故选B.
4.A.
【解析】 如图四边形ABCD,E、N、M、F分别是DA,AB,BC,DC中点,连接AC,DE,
根据三角形中位线定理可得:
EF平行且等于AC的一半,MN平行且等于AC的一半,
根据平行四边形的判定,可知四边形为平行四边形.
故选:A.
5.D.
【解析】连接AE,如图所示,
∵E为BC的中点,
∴BE=CE=BC,又BC=2AD,∴AD=BE=EC,又AD∥BC,
∴四边形ABED为平行四边形,四边形AECD为平行四边形,
又∵∠DCB=90°,∴四边形AECD为矩形,∴∠AEC=90°,即AE⊥BC,∴AE垂直平分BC,
∴AB=AC,即△ABC为等腰三角形,
故选项A不合题意;
∵E为BC的中点,F为AB的中点,∴EF为△ABC的中位线,∴EF∥AC,EF=AC,
又∵四边形ABED为平行四边形,∴AF∥ME,∴四边形AFEM为平行四边形,
又∵AF=AB=AC=EF,∴四边形AFEM为菱形,故选项B不合题意;
过F作FN⊥BC于N点,可得FN∥AE,
又∵F为AB的中点,∴N为BE的中点,∴FN为△ABE的中位线,∴FN=AE,
又∵AE=DC,BE=AD,∴S△BEF=S△ACD,故选项C不合题意;DE不一定平分∠CDF,
故选项D符合题意.
6.B
【解析】∵菱形与矩形都是平行四边形,A, C是平行四边形的性质,
∴二者都具有,故此两个选项都不正确,
由于菱形的对角线互相垂直且平分每一组对角,而矩形的对角线则相等,故选:B
7.B.
【解析】∵△BCE绕点C顺时针方向旋转90°得到△DCF,
∴CE=CF,∠DFC=∠BEC=60°,∠EFC=45°,∴∠EFD=60°-45°=15°.故选B.
8.A.
【解析】如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,∴∠OAD=∠COE,
在△AOD和△OCE中,
,∴△AOD≌△OCE(AAS),∴OE=AD=,CE=OD=1,
∵点C在第二象限,∴点C的坐标为(-,1).
9.B.
【解析】∵BD、GE分别是正方形ABCD,正方形CEFG的对角线,
∴∠ADB=∠CGE=45°,∴∠GDT=180°﹣90°﹣45°=45°,
∴∠DTG=180°﹣∠GDT﹣∠CGE=180°﹣45°﹣45°=90°,
∴△DGT是等腰直角三角形,
∵两正方形的边长分别为4,8,∴DG=8﹣4=4,∴GT=.故选B.
10.D.
【解析】严格按照图中的顺序向上对折,向右对折,从右下角剪去一个四分之一圆,从左上角和左下角各剪去一个直角三角形,展开得到结论.故选D.www.21-cn-jy.com
11.16
【解析】设AB=x,BC=y,根据题意得:,,所以,所以,即矩形ABCD的面积是16.
12.5
【解析】由题意知阴影面积等于矩形面积减去3个空白三角形的面积,设每个小长方形长为a,宽为b,则ab=1.即4a×4b-a×4b-×3a×3b-×3a×3b=16ab-2ab-9ab=5ab=5.
13.16
【解析】∵解方程x2-7x+12=0得:x=3或4
∵对角线长为6,3+3=6,不能构成三角形;∴菱形的边长为4.∴菱形ABCD的周长为4×4=16
14.5
【解析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,∴AC∥MQ,
∵M为BC中点,∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,∴BQ∥CD,BQ=CN,∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,∴CP=AC=3,BP=BD=4,
在Rt△BPC中,由勾股定理得:BC=5,即NQ=5,
∴MP+NP=QP+NP=QN=5,
15..
【解析】连接AC、CF,根据正方形性质求出AC、CF,∠ACD=∠GCF=45°,再求出∠ACF=90°,然后利用勾股定理列式求出AF,再根据直角三角形斜边上的中线等于斜边的一半解答即可.
解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,
∠ACD=∠GCF=45°,∴∠ACF=90°,
由勾股定理得,AF=,
∵H是AF的中点,∴CH=AF=.
16.()6, ()n-1.
【解析】根据第一个正方形的边长为1可以求得第二个正方形的边长,以此类推可以求得正方形的边长满足一定的规律,根据次规律可以求得第n个正方形的边长.
解:∵正方形ABCD的边长为1的正方形,
∴a1=1=()0,
∵AC是正方形ABCD的对角线,∴AC=,∴a2=,
同理可得
a3=
a4=,
…
a7=()6∴an=()n-1.
17.(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】(1)由折叠的性质可得到△ABD≌△EDB,那么∠ADB=∠EBD,所以BF=DF;
(2)根据长方形的性质可得和三角形内角和定理可得∠AEF=∠FBD,再根据平行线的判定即可求解;
(3)先SSS证明△ABD≌△EDB,再根据全等三角形的性质和垂直平分线的性质即可求解.
解:(1)∵△BCD≌△BED,∴∠DBC=∠EBD,
又∵四边形ABCD是长方形,∴AD∥BC,∴∠ADB=∠DBC,∴∠ADB=∠EBD,∴BF=DF.
(2)∵四边形ABCD是长方形,∴AD=BC=BE,
又∵FB=FD,∴FA=FE,∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF+∠AFE=2∠FBD+∠BFD=180°,
∴∠AEF=∠FBD,∴AE∥BD;
(3)∵四边形ABCD是长方形,∴AD=BC=BE,AB=CD=DE,BD=DB,
在△ABD与△EDB中,
∴△ABD≌△EDB(SSS),∴∠ABD=∠EDB,∴GB=GD,
又∵FB=FD,∴GF是BD的垂直平分线,即GH垂直平分BD.
18.(1)见解析(5分)(2)菱形 证明:见解析(5分)
【解析】(1)根据条件证△ABE≌△ADF即可;(2)因为OA=OM,所以证明EF、AM互相垂直平分,从而可判定四边形AEMF是菱形.21·cn·jy·com
解:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,在Rt△ABE和Rt△ADF中,∵AD=AB,AF=AE,∴Rt△ADF≌Rt△ABE(HL)∴BE=DF;(2)解:四边形AEMF是菱形,理由为:证明:∵四边形ABCD是正方形,∴∠BCA=∠DCA=45°,BC=DC,∵BE=DF,∴BC-BE=DC-DF,即CE=CF,在△COE和△COF中CE=CF,∠ACB=∠ACD, OC=OC∴△COE≌△COF(SAS),∴OE=OF,又OM=OA,∴四边形AEMF是平行四边形,∵AE=AF,∴平行四边形AEMF是菱形.www-2-1-cnjy-com
19.见解析
【解析】由菱形的性质得到从而的证.
解:∵ 四边形ABCD是菱形∴
又∵AE=AF,AC为公共边∴∴CE=CF 、
20.(1)证明见试题解析;(2)∠B=30°,证明见试题解析.
【解析】(1)易证∠DEC=∠DFA,即可得CE∥AF,根据CE=AF可得四边形ACEF为平行四边形;【出处:21教育名师】
(2)要使得平行四边形ACEF为菱形,则AC=CE,又∵CE=AB,∴使得AB=2AC即可,根据AB、AC即可求得∠B的值.21*cnjy*com
解:(1)∵DE为BC的垂直平分线,∴∠EDB=90°,BD=DC,
又∵∠ACB=90°,∴DE∥AC,∴E为AB的中点,∴在Rt△ABC中,CE=AE=BE,
∴∠AEF=∠AFE,且∠BED=∠AEF,∴∠DEC=∠DFA,∴AF∥CE,
又∵AF=CE,∴四边形ACEF为平行四边形;
(2)要使得平行四边形ACEF为菱形,则AC=CE即可,
∵DE∥AC,∴∠BED=∠BAC,∠DEC=∠ECA,
又∵∠BED=∠DEC,∴∠EAC=∠ECA,∴AE=EC,又EB=EC,∴AE=EC=EB,
∵CE=AB,∴AC=AB即可,
在Rt△ABC中,∠ACB=90°,∴当∠B=30°时,AB=2AC,
故∠B=30°时,四边形ACEF为菱形.
21.(1)AE=CF (2)∠EGC=80°
【解析】(1)要证AE=CF,若我们能够证明其所在的三角形全等即可。AE位于
△AEB中,CF位于△CFB中,因为四边形ABCD是正方形,则AB=BC,因为
BE⊥BF,则∠ABC=∠EBF=90°,都减去∠EBC,故∠ABE=∠CBF,又因为BE=BF,故可以
由SAS定理得到两个三角形全等。故AE=CF。
(2)由三角形的外角等于和他不相邻的两个内角之和,则∠EGC=∠EBG+∠BEF,由BE⊥BF,
∠FBE=90°,BE=BF,则∠BEF=∠EFB=45°,而∠EBG=90°-∠ABE=90°-55°=35°,故可求出∠EGC=80°。21教育网
解:
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵BE⊥BF,
∴∠FBE=90°,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF,
在△AEB和△CFB中,
∴△AEB≌△CFB(SAS),
∴AE=CF. .
(2)解:∵BE⊥BF,
∴∠FBE=90°,
又∵BE=BF,
∴∠BEF=∠EFB=45°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
又∵∠ABE=55°,
∴∠EBG=90°-55°=35°,
∴∠EGC=∠EBG+∠BEF=45°+35°=80°
22.(1)详见解析 (2)
【解析】
①连接EG,∵AB∥DH,∴∠AEG=∠EGC。∵EF∥GP,∴∠FEG=∠EGP,∴∠AEF=∠PGC,有∵EF=PG,∠A=∠H=,∴ΔAEF≌ΔPGH,∴GH=AE21世纪教育网版权所有
②∵EF=5,cos∠AFE==,∴AF=4,AE=3。∵FD=2,∴AD=DC=6。∵
∴,∵PH=AF=4,∴
23.
【解析】(1)根据正方形的性质得出∠ABC=∠ADF=90°,进而得出△ABE≌△ADF,即可得出AE=AF;21cnjy.com
(2)连接AG,利用全等三角形的判定得出△AEG≌△AFG(SAS),进而得出EG=BE+DG;
(3)首先设AB=5k,GF=6k,再假设BE=x,则CE=6k-x,EG=5k,得出CF=CD+DF=6k+x,CG=CF-GF=6k+x-5k=k+x,进而利用勾股定理得出x的值,进而比较得出答案.
解:(1)正方形ABCD中,AB=AD,
∠ABC=∠ADC=∠BAD= 90°
∴∠ABC=∠ADF=90°,
∵∠EAF=90°∴∠BAE=∠DAF
∴≌,
∴AE=AF
(2)连接AG,
∵点G是斜边MN的中点,
∴∠EAG=∠FAG=45°
AG=AG,则≌
∴EG=GF
∴EG=DG+DF
∵BE=DF
∴EG=BE+DG
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
