圆的有关计算(二)(广东省深圳市南山区)
文档属性
| 名称 | 圆的有关计算(二)(广东省深圳市南山区) |  | |
| 格式 | rar | ||
| 文件大小 | 69.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-07 07:17:00 | ||
图片预览

文档简介
初三数学 快乐学习,轻松进步!!! 09MP02
集训专题:与圆有关的计算(二)
【教学目标】通过作图、识图,探索弧长、扇形及其组合图形面积的计算方法和解题规律.
【重点】正多边形的有关计算,弧长与扇形面积的计算,简单组合图形的周长和面积的计算,以及圆锥的侧面积的计算
【难点】 组合图形面积的计算
【考点】中考中弧长的计算,圆柱、圆锥的侧面积及简单组合图形的面积的计算,多以填空或选择题的形式出现
【知识要点】
1.多边形的有关计算:
设正多边形的边数为n,边长为an,半径为Rn,边心距为rn,中心角为,周长为Pn,面积为Sn,则求:中心角;边心距,周长,面积
2.弧长的计算:如果一个圆的半径为,那么的圆心角所对的弧长为.
3.扇形面积的计算:如果圆的半径为,那么的心角的扇形面积为.
4.圆锥侧面积和全面积:圆锥侧面积等于扇形的面积
【经典例题】
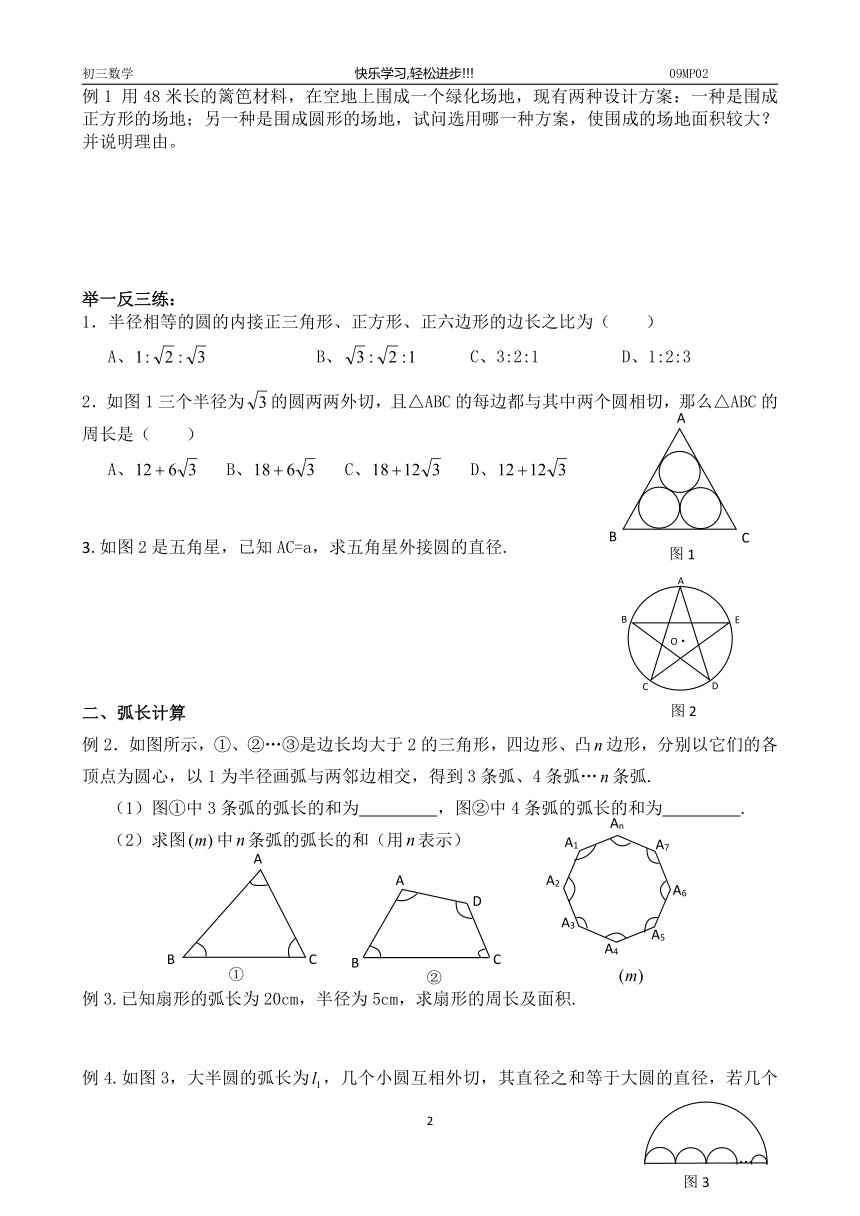
例1 用48米长的篱笆材料,在空地上围成一个绿化场地,现有两种设计方案:一种是围成正方形的场地;另一种是围成圆形的场地,试问选用哪一种方案,使围成的场地面积较大?并说明理由。
举一反三练:
1.半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )
A、 B、 C、3:2:1 D、1:2:3
2.如图1三个半径为的圆两两外切,且△ABC的每边都与其中两个圆相切,那么△ABC的周长是( )
A、 B、 C、 D、
3.如图2是五角星,已知AC=a,求五角星外接圆的直径.
二、弧长计算
例2.如图所示,①、②…③是边长均大于2的三角形,四边形、凸边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…条弧.
(1)图①中3条弧的弧长的和为 ,图②中4条弧的弧长的和为 .
(2)求图中条弧的弧长的和(用表示)
例3.已知扇形的弧长为20cm,半径为5cm,求扇形的周长及面积.
例4.如图3,大半圆的弧长为,几个小圆互相外切,其直径之和等于大圆的直径,若几个小的半圆的总弧长,同下列关系成立的是( )
A、 B、 C、 D、
举一反三练:
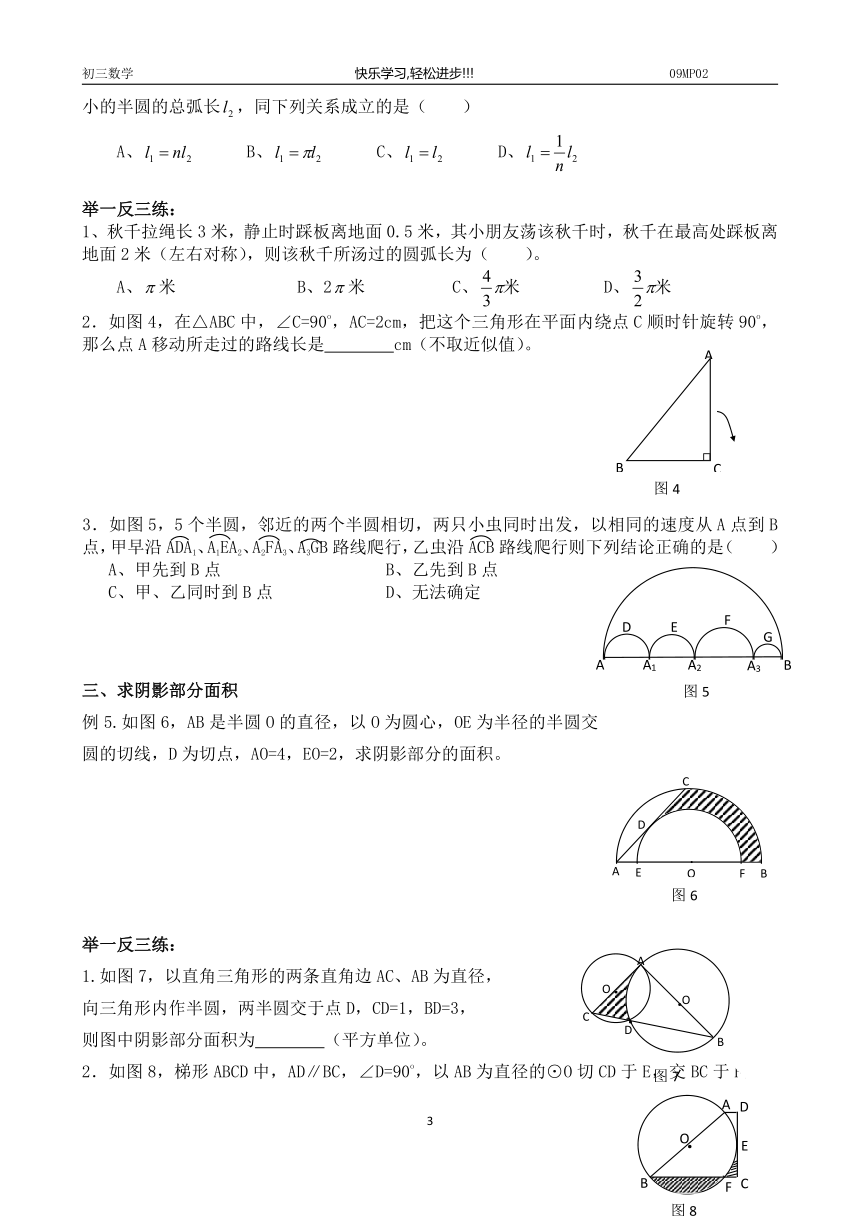
1、秋千拉绳长3米,静止时踩板离地面0.5米,其小朋友荡该秋千时,秋千在最高处踩板离地面2米(左右对称),则该秋千所汤过的圆弧长为( )。
A、米 B、2米 C、 D、
2.如图4,在△ABC中,∠C=90o,AC=2cm,把这个三角形在平面内绕点C顺时针旋转90o,那么点A移动所走过的路线长是 cm(不取近似值)。
3.如图5,5个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲早沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行则下列结论正确的是( )
A、甲先到B点 B、乙先到B点
C、甲、乙同时到B点 D、无法确定
三、求阴影部分面积
例5.如图6,AB是半圆O的直径,以O为圆心,OE为半径的半圆交AB于E、F,弦AC是小圆的切线,D为切点,AO=4,EO=2,求阴影部分的面积。
举一反三练:
1.如图7,以直角三角形的两条直角边AC、AB为直径,
向三角形内作半圆,两半圆交于点D,CD=1,BD=3,
则图中阴影部分面积为 (平方单位)。
2.如图8,梯形ABCD中,AD∥BC,∠D=90o,以AB为直径的⊙O切CD于E,交BC于F,若AB=4cm,AD=1cm,则图中阴影部分面积为 cm2(不用近似值)。
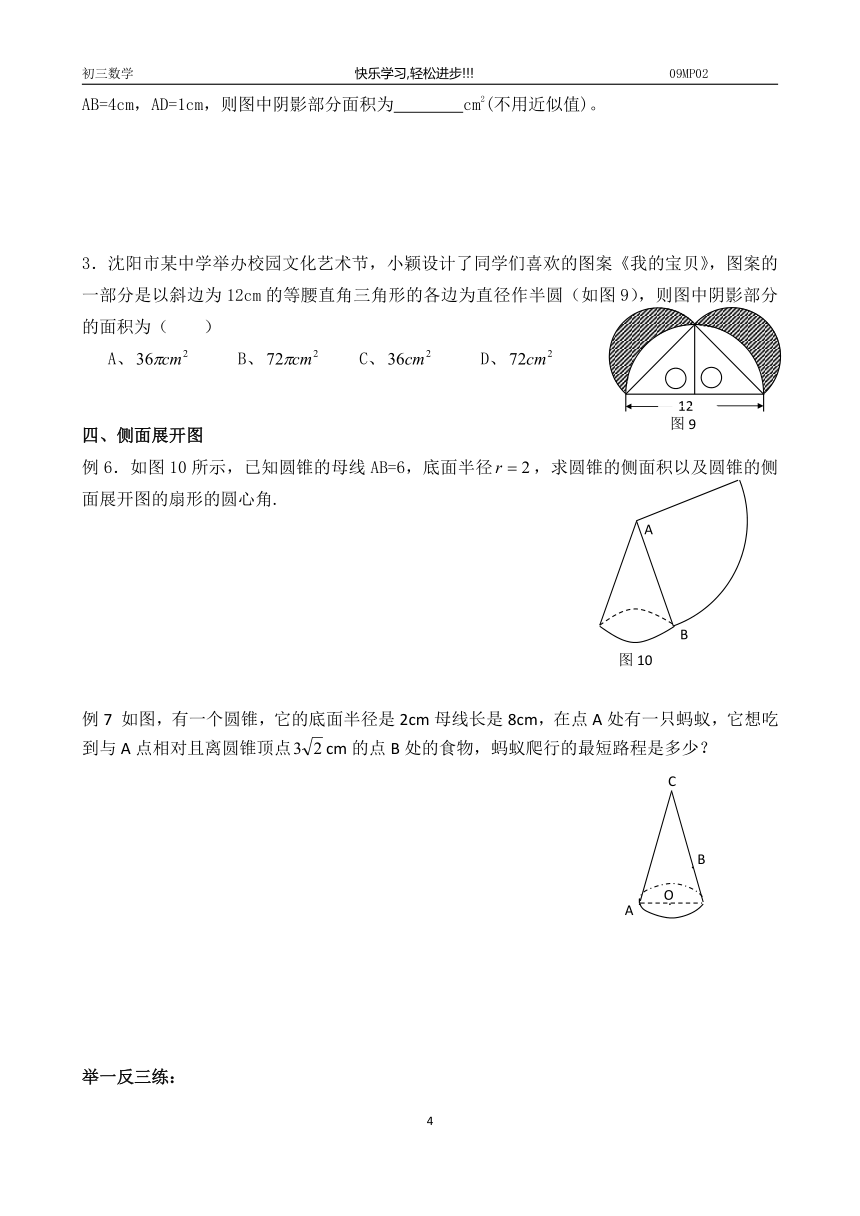
3.沈阳市某中学举办校园文化艺术节,小颖设计了同学们喜欢的图案《我的宝贝》,图案的一部分是以斜边为12cm的等腰直角三角形的各边为直径作半圆(如图9),则图中阴影部分的面积为( )
A、 B、 C、 D、
四、侧面展开图
例6.如图10所示,已知圆锥的母线AB=6,底面半径,求圆锥的侧面积以及圆锥的侧面展开图的扇形的圆心角.
例7 如图,有一个圆锥,它的底面半径是2cm母线长是8cm,在点A处有一只蚂蚁,它想吃到与A点相对且离圆锥顶点cm的点B处的食物,蚂蚁爬行的最短路程是多少?
举一反三练:
1、一个扇形如图11所示,半径为10cm,圆心角为270o,用它做成一个圆锥的侧面,那么圆锥的高为 cm。
2.如图12,粮仓的顶部是圆锥形,这个圆锥底面周长为32m,母线长7m,为防雨
需要在粮仓顶部铺上油毡,则共需油毡 m2。(油毡接缝重合部分不计)
3.小明要制作一个圆锥模型,其侧面是一个半径为9cm,圆心角为240o的扇形纸板制成的,还需要一块圆形纸板做底面,那么这块圆形板的直径为( )
A、15cm B、12cm C、10cm D、9cm
【冲刺练习】
1.计算:
(1)已知圆的面积为,其圆周上一段弧长为,
那么这段弧所对圆心角的度数是 .
(2)如图13所示,AB、CD是⊙O的直径,⊙O的半径为R,AB⊥CD,
以B为圆心,以BC为半径作CED,则CED与CAD围成的新月形ACED的面积为 .
(3)如图14,某学校建一个喷泉水池,设计的底面边长为4m的正六边形,池底是水磨石地面,现用的磨光机的磨头是半径为2dm的圆形砂轮,磨池底时磨头磨不到的部分的面积为 .
2.如图15所示,某传送带的一个转动轮的半径为20cm,当物体从A传送20cm到B时,这个转动轮转了 度.(取3.14,结果保留四个有效数字
3.如图16,在Rt△ABC中,∠C=90o,∠A=60o,AC=,将△ABC绕点B旋转至△A’BC’的位置,且使点A、B、C’三点在同一条直线上,则点A经过的最短路线的长是 cm.
4.如图17,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.
5.一个圆锥的高为,侧面展开图是半圆,求(1)圆锥的母线与底面半径之比;(2)锥角的大小;(3)圆锥的表面积.
6.有一直径为的圆形纸片,要从中剪出一个最大的圆心角是的扇形ABC,如图18所示.
(1)求被剪掉的阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
(3)求圆锥的全面积.
7.已知⊙O的半径为R,直径AB⊥直径CD,以B为圆心,以BD为半径作⊙B交AB于点E,交AB的延长线于点F,联结DB并延长交⊙B于点M,联结MA交⊙O于点N,交CD于点H,交⊙B于点G.(1)求图中阴影部分的面积S;(2)求证:.
【作业】日期 姓名 完成时间 成绩
1.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚,
如图19所示,那么B点从开始至结束(到达图中所示的位置)
所走过的路径长度为( ).
A、 B、 C、4 D、
2.如图20所示,正方形的边长为,以各边为直径在正方形内画半圆,所围成的图形(阴影部分)的面积为( ).
A、 B、 C、 D、
3.如图21所示,在同心圆中,两圆半径分别为2、1,,则阴影部分的面积为( ).
A、 B、 C、 D、
4.如图22所示,是等腰直角三角形,,⊙A与BC相切,则图中阴影部分的面积为( ).
A、 B、 C、 D、
5.如图23所示,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积为
6.半径为8的半圆是一个圆锥的侧面展开图,那么这个圆锥的底面半径是( ).
A、16 B、8 C、4 D、2
7.一个扇形的圆心角是,它的面积为,那么这个扇形的半径是( ).
A、 B、 C、 D、
8.如果圆柱的底面半径为4cm,母线长为5cm,那么它的侧面积为( ).
A、 B、 C、 D、
9.如图24所示,在矩形ABCD中,AD=2,以B为圆心,BC长为半径画弧交AD于点F.
(1)若CF长为,求圆心角的度数;
(2)求图中阴影部分的面积(结果保留根号及的形式)
10.如图所示,在一个物体的横截面为中,,BC=1米.工人师傅要把此物体搬一墙边,先将AB边放在地面(直线)上,再按顺时针方向绕点B翻转到的位置(上),最后沿射线的方向平移到的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)
(1)请直接写出AB、AC的长;
(2)画出在搬动此物体的整个过程中A点所经过的路径,并求出该路径的长度(精确到0.1米)
A
B
C
A
B
C
D
E
C
O·
…
A
B
C
A
A1
A2
A3
B
D
E
F
G
·
A
E
O
F
B
D
C
A
B
C
D
·
·
·
O2
O1
·
A
D
C
E
F
B
O
12
A
B
O
A
C
D
O
E
B
A
B
·
·
·
B
·
O
A
·
A
B
C
A
B
C
O
·
·
M
D
·
N
·
B
A
C
O
B
A
·
A
B
C
①
A
D
C
B
②
A11
A21
A31
A41
A51
A61
A71
An
B
·
·
·
H
N
M
A
B
C
D
F
图24
A
B
O
A
C
B
图20
图21
图22
A
B
C
B
A
C
B
图19
图2
图1
图3
图23
图18
图4
图5
图6
图7
图8
图9
图10
图11
图12
图14
图13
A1
B1
C1
C2
A2
B
A
图17
图16
图15
C
A
C
D
E
F
O
G
1
集训专题:与圆有关的计算(二)
【教学目标】通过作图、识图,探索弧长、扇形及其组合图形面积的计算方法和解题规律.
【重点】正多边形的有关计算,弧长与扇形面积的计算,简单组合图形的周长和面积的计算,以及圆锥的侧面积的计算
【难点】 组合图形面积的计算
【考点】中考中弧长的计算,圆柱、圆锥的侧面积及简单组合图形的面积的计算,多以填空或选择题的形式出现
【知识要点】
1.多边形的有关计算:
设正多边形的边数为n,边长为an,半径为Rn,边心距为rn,中心角为,周长为Pn,面积为Sn,则求:中心角;边心距,周长,面积
2.弧长的计算:如果一个圆的半径为,那么的圆心角所对的弧长为.
3.扇形面积的计算:如果圆的半径为,那么的心角的扇形面积为.
4.圆锥侧面积和全面积:圆锥侧面积等于扇形的面积
【经典例题】
例1 用48米长的篱笆材料,在空地上围成一个绿化场地,现有两种设计方案:一种是围成正方形的场地;另一种是围成圆形的场地,试问选用哪一种方案,使围成的场地面积较大?并说明理由。
举一反三练:
1.半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )
A、 B、 C、3:2:1 D、1:2:3
2.如图1三个半径为的圆两两外切,且△ABC的每边都与其中两个圆相切,那么△ABC的周长是( )
A、 B、 C、 D、
3.如图2是五角星,已知AC=a,求五角星外接圆的直径.
二、弧长计算
例2.如图所示,①、②…③是边长均大于2的三角形,四边形、凸边形,分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…条弧.
(1)图①中3条弧的弧长的和为 ,图②中4条弧的弧长的和为 .
(2)求图中条弧的弧长的和(用表示)
例3.已知扇形的弧长为20cm,半径为5cm,求扇形的周长及面积.
例4.如图3,大半圆的弧长为,几个小圆互相外切,其直径之和等于大圆的直径,若几个小的半圆的总弧长,同下列关系成立的是( )
A、 B、 C、 D、
举一反三练:
1、秋千拉绳长3米,静止时踩板离地面0.5米,其小朋友荡该秋千时,秋千在最高处踩板离地面2米(左右对称),则该秋千所汤过的圆弧长为( )。
A、米 B、2米 C、 D、
2.如图4,在△ABC中,∠C=90o,AC=2cm,把这个三角形在平面内绕点C顺时针旋转90o,那么点A移动所走过的路线长是 cm(不取近似值)。
3.如图5,5个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲早沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行则下列结论正确的是( )
A、甲先到B点 B、乙先到B点
C、甲、乙同时到B点 D、无法确定
三、求阴影部分面积
例5.如图6,AB是半圆O的直径,以O为圆心,OE为半径的半圆交AB于E、F,弦AC是小圆的切线,D为切点,AO=4,EO=2,求阴影部分的面积。
举一反三练:
1.如图7,以直角三角形的两条直角边AC、AB为直径,
向三角形内作半圆,两半圆交于点D,CD=1,BD=3,
则图中阴影部分面积为 (平方单位)。
2.如图8,梯形ABCD中,AD∥BC,∠D=90o,以AB为直径的⊙O切CD于E,交BC于F,若AB=4cm,AD=1cm,则图中阴影部分面积为 cm2(不用近似值)。
3.沈阳市某中学举办校园文化艺术节,小颖设计了同学们喜欢的图案《我的宝贝》,图案的一部分是以斜边为12cm的等腰直角三角形的各边为直径作半圆(如图9),则图中阴影部分的面积为( )
A、 B、 C、 D、
四、侧面展开图
例6.如图10所示,已知圆锥的母线AB=6,底面半径,求圆锥的侧面积以及圆锥的侧面展开图的扇形的圆心角.
例7 如图,有一个圆锥,它的底面半径是2cm母线长是8cm,在点A处有一只蚂蚁,它想吃到与A点相对且离圆锥顶点cm的点B处的食物,蚂蚁爬行的最短路程是多少?
举一反三练:
1、一个扇形如图11所示,半径为10cm,圆心角为270o,用它做成一个圆锥的侧面,那么圆锥的高为 cm。
2.如图12,粮仓的顶部是圆锥形,这个圆锥底面周长为32m,母线长7m,为防雨
需要在粮仓顶部铺上油毡,则共需油毡 m2。(油毡接缝重合部分不计)
3.小明要制作一个圆锥模型,其侧面是一个半径为9cm,圆心角为240o的扇形纸板制成的,还需要一块圆形纸板做底面,那么这块圆形板的直径为( )
A、15cm B、12cm C、10cm D、9cm
【冲刺练习】
1.计算:
(1)已知圆的面积为,其圆周上一段弧长为,
那么这段弧所对圆心角的度数是 .
(2)如图13所示,AB、CD是⊙O的直径,⊙O的半径为R,AB⊥CD,
以B为圆心,以BC为半径作CED,则CED与CAD围成的新月形ACED的面积为 .
(3)如图14,某学校建一个喷泉水池,设计的底面边长为4m的正六边形,池底是水磨石地面,现用的磨光机的磨头是半径为2dm的圆形砂轮,磨池底时磨头磨不到的部分的面积为 .
2.如图15所示,某传送带的一个转动轮的半径为20cm,当物体从A传送20cm到B时,这个转动轮转了 度.(取3.14,结果保留四个有效数字
3.如图16,在Rt△ABC中,∠C=90o,∠A=60o,AC=,将△ABC绕点B旋转至△A’BC’的位置,且使点A、B、C’三点在同一条直线上,则点A经过的最短路线的长是 cm.
4.如图17,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=a,ON、CD分别为两圆的半径,求阴影部分的面积.
5.一个圆锥的高为,侧面展开图是半圆,求(1)圆锥的母线与底面半径之比;(2)锥角的大小;(3)圆锥的表面积.
6.有一直径为的圆形纸片,要从中剪出一个最大的圆心角是的扇形ABC,如图18所示.
(1)求被剪掉的阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
(3)求圆锥的全面积.
7.已知⊙O的半径为R,直径AB⊥直径CD,以B为圆心,以BD为半径作⊙B交AB于点E,交AB的延长线于点F,联结DB并延长交⊙B于点M,联结MA交⊙O于点N,交CD于点H,交⊙B于点G.(1)求图中阴影部分的面积S;(2)求证:.
【作业】日期 姓名 完成时间 成绩
1.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚,
如图19所示,那么B点从开始至结束(到达图中所示的位置)
所走过的路径长度为( ).
A、 B、 C、4 D、
2.如图20所示,正方形的边长为,以各边为直径在正方形内画半圆,所围成的图形(阴影部分)的面积为( ).
A、 B、 C、 D、
3.如图21所示,在同心圆中,两圆半径分别为2、1,,则阴影部分的面积为( ).
A、 B、 C、 D、
4.如图22所示,是等腰直角三角形,,⊙A与BC相切,则图中阴影部分的面积为( ).
A、 B、 C、 D、
5.如图23所示,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积为
6.半径为8的半圆是一个圆锥的侧面展开图,那么这个圆锥的底面半径是( ).
A、16 B、8 C、4 D、2
7.一个扇形的圆心角是,它的面积为,那么这个扇形的半径是( ).
A、 B、 C、 D、
8.如果圆柱的底面半径为4cm,母线长为5cm,那么它的侧面积为( ).
A、 B、 C、 D、
9.如图24所示,在矩形ABCD中,AD=2,以B为圆心,BC长为半径画弧交AD于点F.
(1)若CF长为,求圆心角的度数;
(2)求图中阴影部分的面积(结果保留根号及的形式)
10.如图所示,在一个物体的横截面为中,,BC=1米.工人师傅要把此物体搬一墙边,先将AB边放在地面(直线)上,再按顺时针方向绕点B翻转到的位置(上),最后沿射线的方向平移到的位置,其平移的距离为线段AC的长度(此时恰好靠在墙边)
(1)请直接写出AB、AC的长;
(2)画出在搬动此物体的整个过程中A点所经过的路径,并求出该路径的长度(精确到0.1米)
A
B
C
A
B
C
D
E
C
O·
…
A
B
C
A
A1
A2
A3
B
D
E
F
G
·
A
E
O
F
B
D
C
A
B
C
D
·
·
·
O2
O1
·
A
D
C
E
F
B
O
12
A
B
O
A
C
D
O
E
B
A
B
·
·
·
B
·
O
A
·
A
B
C
A
B
C
O
·
·
M
D
·
N
·
B
A
C
O
B
A
·
A
B
C
①
A
D
C
B
②
A11
A21
A31
A41
A51
A61
A71
An
B
·
·
·
H
N
M
A
B
C
D
F
图24
A
B
O
A
C
B
图20
图21
图22
A
B
C
B
A
C
B
图19
图2
图1
图3
图23
图18
图4
图5
图6
图7
图8
图9
图10
图11
图12
图14
图13
A1
B1
C1
C2
A2
B
A
图17
图16
图15
C
A
C
D
E
F
O
G
1
同课章节目录
