浙教版数学2014-2015学年九下单元精品卷 第二章 直线与圆的位置关系(基础检测)含精析
文档属性
| 名称 | 浙教版数学2014-2015学年九下单元精品卷 第二章 直线与圆的位置关系(基础检测)含精析 |  | |
| 格式 | zip | ||
| 文件大小 | 260.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-25 11:32:46 | ||
图片预览



文档简介
【浙教版】数学2014-2015学年九下“单元精品卷”(基础检测卷)
第二章 直线与圆的位置关系
题 号
仔细选一选
认真填一填
全面答一答
总 分
得 分
一、仔细选一选。(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内.注意可以用多种不同的方法来选取正确答案.
1.如图,A,B,C是☉O上的三点,且∠ABC=70°,则∠AOC的度数是( )
A.35° B.140° C.70° D.70°或140°
2.如图,AB是⊙O的弦,AC是⊙O的切线,切点为A,BC经过圆心O.若∠B=25o,则∠C的大小等于( )2·1·c·n·j·y
A.20o B.40o C.25o D.50
3.已知⊙O的半径是6cm,点O到同一平面内直线L的距离为5cm,则直线L与⊙O的位置关系是( )21·世纪*教育网
A.相交 B.相切 C.相离 D.无法判断
4.在平面直角坐标系中,以点(3,-5)为圆心,为半径的圆上有且仅有两点到轴所在直线的距离等于1,则圆的半径的取值范围是( )【版权所有:21教育】
A. B. C. D.
5.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,联结BC,若∠A=36°,则∠C等于( )
A.36° B.54° C.60° D.27°
6.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )
A.55° B.60° C.65° D.70°
7.已知⊙O1的半径R为7cm,⊙O2的半径为4cm,两圆的圆心距O1O2为3cm,则这两圆的位置关系是( )
A.相交 B.内含 C.内切 D.外切
8.如果半径分别为2cm和3cm的两圆外切,那么这两个圆的圆心距是 ( )
A.1cm B.5cm C.1cm或5cm D.小于1cm.
9.已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是( )
A.0<d<1 B.d>5 C.0<d<1或d>5 D.0≤d<1或d>5
10.如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )
A.60° B.45° C.30° D.20°
二、认真填一填。(本题有6个小题,每小题4分,共24分)
要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.
11.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作DC切⊙O于点C,若∠A=35°,则∠D=________.
12.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为 .
13.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是 .
14.已知⊙O1和⊙O2的半径分别是一元二次方程(x﹣1)(x﹣2)=0的两根,且O1O2=2,则⊙O1和⊙O2的位置关系是 .
15.在平面直角坐标系xOy中,已知点A(2,0),⊙A的半径是2,⊙P的半径是1,满足与⊙A及y轴都相切的⊙P有 个.
16.如图,以O为圆心的两个同心圆中,大圆与小圆的半径分别为3cm和1cm,若圆P与这两个圆都相切,则圆P的半径为 cm.【来源:21·世纪·教育·网】
三、全面答一答。(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.21·cn·jy·com
17.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,∠CBD=30°,则图中阴影部分的面积;
(3)过点B作⊙O的切线交CD的延长线于点E若BC=12,tan∠CDA=,求BE的长.
18.如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
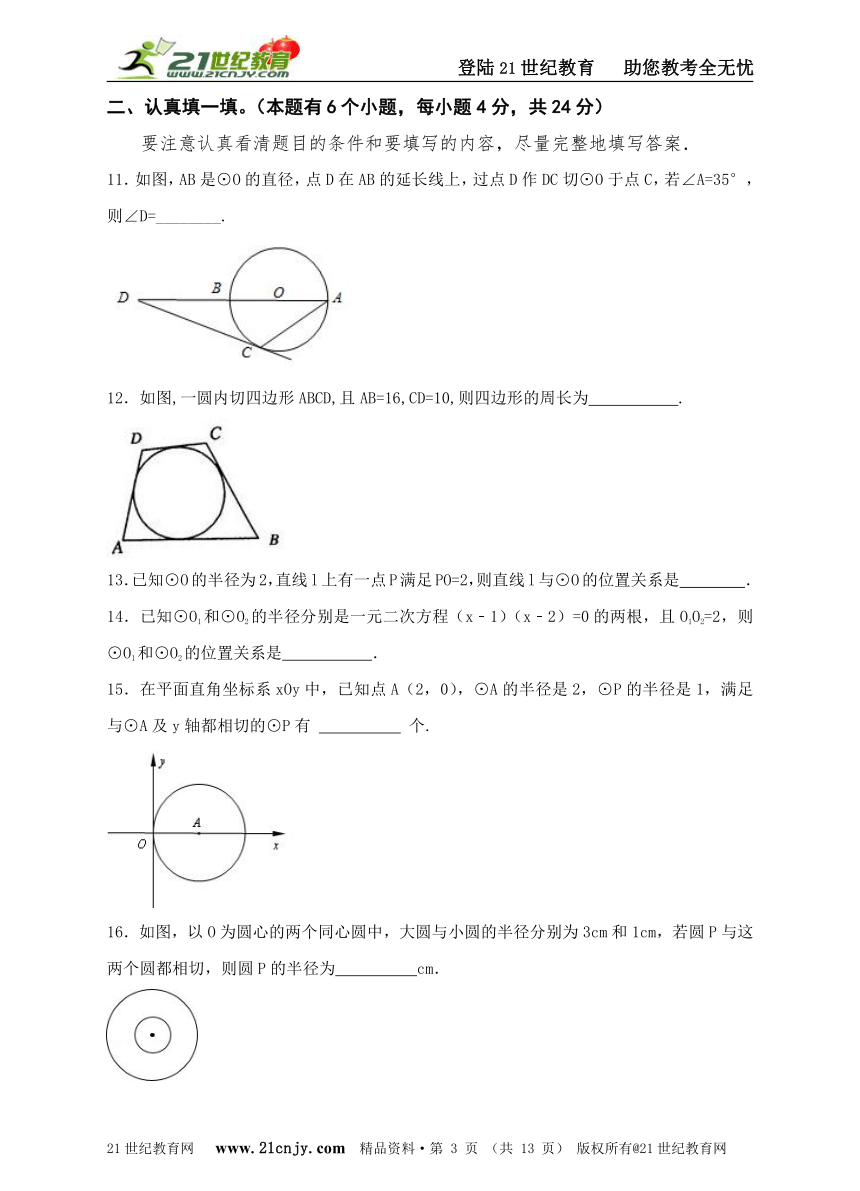
19.如图所示,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切与点B,连接BA并延长交⊙A于点D,交ON于点E。21世纪教育网版权所有
(1)求证:ON是⊙A的切线;
(2)若∠MON=60°,求图中阴影部分的面积(结果保留π)。
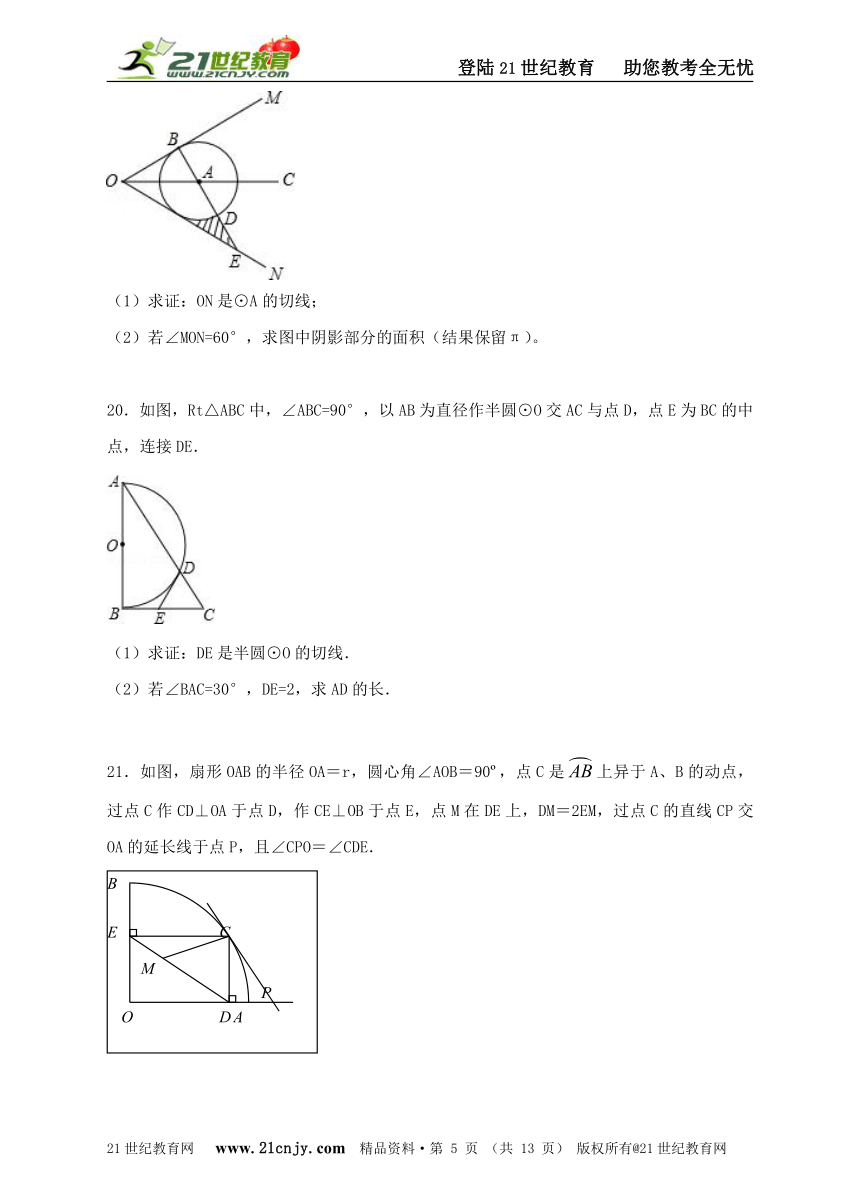
20.如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.www-2-1-cnjy-com
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
21.如图,扇形OAB的半径OA=r,圆心角∠AOB=90o,点C是上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线CP交OA的延长线于点P,且∠CPO=∠CDE.2-1-c-n-j-y
(1)试说明:DM=r;
(2)试说明:直线CP是扇形OAB所在圆的切线;
22.如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线与x轴、y轴分别相交于点D、点E,连接AC并延长与y轴相交于点B,点B的坐标为(0,)。【出处:21教育名师】
(1)求证:OE=CE;
(2)请判断直线CD与⊙P位置关系,证明你的结论,并请求出⊙P的半径长。
23.已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
参考答案与详解
1.B
【解析】由A、B、C是⊙O上的三点,且∠ABC=70°,因此根据同弧所对圆周角是它所对圆周角的一半,得∠AOC=2∠ABC=2×70°=140°.故选B21教育名师原创作品
2.B
【解析】由切线的性质连接OA,则OA⊥AC,从而得到∠AOC=2∠B,再根据直角三角形的两锐角互余,可以求得∠C.21*cnjy*com
3.A
【解析】设圆的半径为r,点O到直线l的距离为d,
∵d=5,r=6,∴d<r,∴直线l与圆相交.故选A
4.D.
【解析】根据题意可知到x轴所在直线的距离等于1的点的集合分别是直线y=1和直线y=-1,
若以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1,
那么该圆与直线y=-1必须是相交的关系,与直线y=1必须是相离的关系,
所以r的取值范围是|-5|-|-1|<r<|-5|+1,即4<r<6.故选D.
5.D.
【解析】∵AB与⊙O相切于点B,∴∠ABO=90°,
∵∠A=36°,∴∠BOA=54°,∴由圆周角定理得:∠C=∠BOA=27°,故选D.
6.C.
【解析】 ∵∠A=100°,∠C=30°,∴∠B=50°,
∵∠BDO=∠BEO,∴∠DOE=130°,∴∠DFE=65°.故选C.
7.C
【解析】因为⊙O1的半径R为7cm,⊙O2的半径为4cm,两圆的圆心距O1O2为3cm,所以d=R-r,所以两圆内切,故选:C.21教育网
8.B.
【解析】∵半径分别为2cm和3cm的两圆外切,∴两个圆的圆心距d=3+2=5cm.故选B.
9.D
【解析】若两圆没有公共点,则可能外离或内含,
外离时的数量关系应满足d>5;
内含时的数量关系应满足0≤d<1.
10.C.
11.20o
【解析】如图,∵∠A=35°,∴∠COD=2∠A=70°.
又∵DC切⊙O于点C,∴∠OCD=90°,∴∠D=90°﹣∠COD=20°.
12.52
【解析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.
根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=52故填:52
13.相切或相交.
【解析】根据直线与圆的位置关系来判定.判断直线和圆的位置关系:①直线l和⊙O相交?d<r;②直线l和⊙O相切?d=r;③直线l和⊙O相离?d>r.分OP垂直于直线l,OP不垂直直线l两种情况讨论.
当OP垂直于直线l时,即圆心O到直线l的距离d=2=r,⊙O与l相切;
当OP不垂直于直线l时,即圆心O到直线l的距离d<2=r,⊙O与直线l相交.
故直线l与⊙O的位置关系是相切或相交.
14.相交
【解析】本题可根据方程解出两个半径的值,将两个半径的和或差与圆心距比较,若d>R+r则两圆相离,若d=R+r则两圆外切,若d=R﹣r则两圆内切,若R﹣r<d<R+r则两圆相交.本题可把半径的值代入,看符合哪一种情况.
解:解方程(x﹣1)(x﹣2)=0,得x1=1,x2=2,
∵2﹣1=1<2<2+1=3,所以两圆相交.
15.4.
【解析】分两圆内切和两圆外切两种情况讨论即可得到⊙P的个数.
如图,
满足条件的⊙P有4个.
16.1或2.
【解析】∵由题意,圆P与这两个圆都相切,∴两种情形:
若圆P与两圆均外切,如答图1所示,此时圆P的半径=(3﹣1)=1cm;
若圆P与两圆均内切,如答图2所示,此时圆P的半径=(3+1)=2cm.
综上所述,圆P的半径为1cm或2cm.
17.(1)见解析 (2)- (3)5
【解析】(1)连接OD、OE,根据∠ADO+∠DBA=90°以及∠∠CDA=∠CBD得出∠ODC=90°;(2)阴影部分的面积等于△OCD的面积减去扇形ODA的面积进行计算;(3)将∠CDA转化成∠OEB,然后利用勾股定理进行求解.【来源:21cnj*y.co*m】
解:(1)证明:连OD,OE,∵AB为直径,∴∠ADB=90°,即∠ADO+∠BDO=90°,
又∵∠CDA=∠CBD,而∠CBD=∠BDO,∴∠BDO=∠CDA,∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
∵OD=1,∠CBD=30° ∴∠DOC=60° ∴∠C=30° ∴OC=2,CD=
∴△OCD的面积= 扇形ODA的面积= ∴阴影部分的面积=-;
(3)∵EB为⊙O的切线,∴ED=EB,OE⊥DB,∴∠ABD+∠DBE=90°,
∠OEB+∠DBE=90°,∴∠ABD=∠OEB,∴∠CDA=∠OEB.而tan∠CDA=,
∴tan∠OEB==,∵Rt△CDO∽Rt△CBE,∴,∴CD=×12=8,
在Rt△CBE中,设BE=x,∴(x+8)2=x2+122,解得x=5.即BE的长为5.
18.见解析
【解析】(1)连接OD,根据EF切⊙O于点D,可得OD⊥EF,又BH⊥EF,所以OD∥BH,然后证明∠ODB=∠OBD=∠DBH即可;(2)过点O作OG⊥BC于点G,由垂径定理和勾股定理可求出圆心O到BC的距离.
解:(1)证明:连接OD.
∵EF是⊙O的切线,∴OD⊥EF.
又∵BH⊥EF,∴OD∥BH,∴∠ODB=∠DBH.
而OD=OB,∴∠ODB=∠OBD,∴∠OBD=∠DBH,∴BD平分∠ABH.
(2)过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG=.
19.(1)证明见解析;(2)2-.
【解析】 (1)首先过点A作AF⊥ON于点F,易证得AF=AB,即可得ON是⊙A的切线;
(2)由∠MON=60°,AB⊥OM,可求得AF的长,又由S阴影=S△AEF-S扇形ADF,即可求得答案.www.21-cn-jy.com
解:(1)证明:过点A作AF⊥ON于点F,
∵⊙A与OM相切于点B,∴AB⊥OM,
∵OC平分∠MON,∴AF=AB=2,∴ON是⊙A的切线;
(2)解:∵∠MON=60°,AB⊥OM,∴∠OEB=30°,∴AF⊥ON,∴∠FAE=60°,
在Rt△AEF中,tan∠FAE=,∴EF=AF?tan60°=2,
∴S阴影=S△AEF-S扇形ADF=AF?EF-×π×AF2=2-.
20.见解析
【解析】(1)连结OD,根据条件证明即可;(2)根据条件可得BC=2DE=4,Rt△ABC中,先由∠BAC=30°,得AC=2 BC =8,再根据条件可证△EDC为等边三角形,可得出DC=2, AD=AC-CD=6.
解:(1)证明:连接OD,OE,
∵AB为圆O的直径,∴∠ADB=∠BDC=90°,在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,OB=OD,OE=OE,BE=DE,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,所以DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,∴BC= AC,∵BC=2DE=4,∴AC=8,又∵∠C=60°,DE=DC,∴△DEC为等边三角形,即DC=DE=2,所以AD=AC-DC=6.
21.(1)见解析(5分) (2)见解析(5分)
【解析】(1)连接OC,可证明四边形ODCE是矩形,所以DE=OC=r,又DM=2EM,所以DM=DE;(2)根据条件证明PC⊥OC即可.
解:(1)证明:连接OC,∵点C是上异于A、B的点,又CD⊥OA于点D,CE⊥OB于点E,∴∠ODC=∠OEC=∠AOB=90°,∴四边形ODCE是矩形,∴DE=OC.∵OC=OA=r,∴DE=r.又∵DM=2EM,∴DM=r;(2)证明:设OC与DE交于点F,则在矩形ODCE中,FC=FD,∴∠CDE=∠DCO,又∵∠CPD+∠PCD=90°,∠CPD=∠CDE,∴∠DCO+∠PCD=90°,即PC⊥OC于点C,又∵OC为扇形OAB的半径,∴PC是扇形OAB所在圆的切线.
22.(2) 直线CD是⊙P的切线, r=6
【解析】(1)连接OC,利用已知条件计算出CE和OB的长度,再证明△BCO为直角三角形,利用:直角三角形斜边上的中线等于斜边的一半即可证明OE=CE;
(2)①直线CD是⊙P的切线,证明PC⊥CD.②设⊙P的半径为r,则在Rt△PCD中,由勾股定理得到关于r的方程,求出r即可.
解:
证明:连结OC,
∵ 直线y=x+2与y轴相交于点E,∴点E的坐标为(0,2),即OE=2。
又∵点B的坐标为(0,4),∴OB=4,∴ BE=OE=2,
又∵OA是⊙P的直径,∴ ∠ACO=90o,即OC⊥AB,
∴OE=CE(直角三角形斜边上的中线等于斜边的一半).
(2)直线CD是⊙P的切线.
证明:连结PC、PE,由①可知:OE=CE.
在△POE和△PCE,∴ △POE≌△PCE,∴∠POE=∠PCE.
又∵x轴⊥y轴,∴∠POE=∠PCE=90o,∴PC⊥CE,即:PC⊥CD。
又∵直线CD经过半径PC的外端点C,∴直线CD是⊙P的切线。
∵ 对,
当y=0时,,即OD=6,
在Rt△DOE中,,
∴ CD=DE+EC=DE+OE=。
设⊙P的半径为r,则在Rt△PCD中,由勾股定理知PC2+CD2=PD2,即r2+()2=(6+r)2,
解得r=6,即⊙P的半径长为6。
23.(1)30°;(2)18°.
【解析】(1)如图①,首先连接OC,根据当直线l与⊙O相切于点C,AD⊥l于点D.易证得OC∥AD,继而可求得∠BAC=∠DAC=30°;21cnjy.com
(2)如图②,连接BF,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠AFB=90°,由三角形外角的性质,可求得∠AEF的度数,又由圆的内接四边形的性质,求得∠B的度数,继而求得答案. 21*cnjy*com
第二章 直线与圆的位置关系
题 号
仔细选一选
认真填一填
全面答一答
总 分
得 分
一、仔细选一选。(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内.注意可以用多种不同的方法来选取正确答案.
1.如图,A,B,C是☉O上的三点,且∠ABC=70°,则∠AOC的度数是( )
A.35° B.140° C.70° D.70°或140°
2.如图,AB是⊙O的弦,AC是⊙O的切线,切点为A,BC经过圆心O.若∠B=25o,则∠C的大小等于( )2·1·c·n·j·y
A.20o B.40o C.25o D.50
3.已知⊙O的半径是6cm,点O到同一平面内直线L的距离为5cm,则直线L与⊙O的位置关系是( )21·世纪*教育网
A.相交 B.相切 C.相离 D.无法判断
4.在平面直角坐标系中,以点(3,-5)为圆心,为半径的圆上有且仅有两点到轴所在直线的距离等于1,则圆的半径的取值范围是( )【版权所有:21教育】
A. B. C. D.
5.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,联结BC,若∠A=36°,则∠C等于( )
A.36° B.54° C.60° D.27°
6.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )
A.55° B.60° C.65° D.70°
7.已知⊙O1的半径R为7cm,⊙O2的半径为4cm,两圆的圆心距O1O2为3cm,则这两圆的位置关系是( )
A.相交 B.内含 C.内切 D.外切
8.如果半径分别为2cm和3cm的两圆外切,那么这两个圆的圆心距是 ( )
A.1cm B.5cm C.1cm或5cm D.小于1cm.
9.已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是( )
A.0<d<1 B.d>5 C.0<d<1或d>5 D.0≤d<1或d>5
10.如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )
A.60° B.45° C.30° D.20°
二、认真填一填。(本题有6个小题,每小题4分,共24分)
要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.
11.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作DC切⊙O于点C,若∠A=35°,则∠D=________.
12.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为 .
13.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是 .
14.已知⊙O1和⊙O2的半径分别是一元二次方程(x﹣1)(x﹣2)=0的两根,且O1O2=2,则⊙O1和⊙O2的位置关系是 .
15.在平面直角坐标系xOy中,已知点A(2,0),⊙A的半径是2,⊙P的半径是1,满足与⊙A及y轴都相切的⊙P有 个.
16.如图,以O为圆心的两个同心圆中,大圆与小圆的半径分别为3cm和1cm,若圆P与这两个圆都相切,则圆P的半径为 cm.【来源:21·世纪·教育·网】
三、全面答一答。(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.21·cn·jy·com
17.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,∠CBD=30°,则图中阴影部分的面积;
(3)过点B作⊙O的切线交CD的延长线于点E若BC=12,tan∠CDA=,求BE的长.
18.如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
19.如图所示,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切与点B,连接BA并延长交⊙A于点D,交ON于点E。21世纪教育网版权所有
(1)求证:ON是⊙A的切线;
(2)若∠MON=60°,求图中阴影部分的面积(结果保留π)。
20.如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.www-2-1-cnjy-com
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
21.如图,扇形OAB的半径OA=r,圆心角∠AOB=90o,点C是上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线CP交OA的延长线于点P,且∠CPO=∠CDE.2-1-c-n-j-y
(1)试说明:DM=r;
(2)试说明:直线CP是扇形OAB所在圆的切线;
22.如图,点A在x轴的正半轴上,以OA为直径作⊙P,C是⊙P上一点,过点C的直线与x轴、y轴分别相交于点D、点E,连接AC并延长与y轴相交于点B,点B的坐标为(0,)。【出处:21教育名师】
(1)求证:OE=CE;
(2)请判断直线CD与⊙P位置关系,证明你的结论,并请求出⊙P的半径长。
23.已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
参考答案与详解
1.B
【解析】由A、B、C是⊙O上的三点,且∠ABC=70°,因此根据同弧所对圆周角是它所对圆周角的一半,得∠AOC=2∠ABC=2×70°=140°.故选B21教育名师原创作品
2.B
【解析】由切线的性质连接OA,则OA⊥AC,从而得到∠AOC=2∠B,再根据直角三角形的两锐角互余,可以求得∠C.21*cnjy*com
3.A
【解析】设圆的半径为r,点O到直线l的距离为d,
∵d=5,r=6,∴d<r,∴直线l与圆相交.故选A
4.D.
【解析】根据题意可知到x轴所在直线的距离等于1的点的集合分别是直线y=1和直线y=-1,
若以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1,
那么该圆与直线y=-1必须是相交的关系,与直线y=1必须是相离的关系,
所以r的取值范围是|-5|-|-1|<r<|-5|+1,即4<r<6.故选D.
5.D.
【解析】∵AB与⊙O相切于点B,∴∠ABO=90°,
∵∠A=36°,∴∠BOA=54°,∴由圆周角定理得:∠C=∠BOA=27°,故选D.
6.C.
【解析】 ∵∠A=100°,∠C=30°,∴∠B=50°,
∵∠BDO=∠BEO,∴∠DOE=130°,∴∠DFE=65°.故选C.
7.C
【解析】因为⊙O1的半径R为7cm,⊙O2的半径为4cm,两圆的圆心距O1O2为3cm,所以d=R-r,所以两圆内切,故选:C.21教育网
8.B.
【解析】∵半径分别为2cm和3cm的两圆外切,∴两个圆的圆心距d=3+2=5cm.故选B.
9.D
【解析】若两圆没有公共点,则可能外离或内含,
外离时的数量关系应满足d>5;
内含时的数量关系应满足0≤d<1.
10.C.
11.20o
【解析】如图,∵∠A=35°,∴∠COD=2∠A=70°.
又∵DC切⊙O于点C,∴∠OCD=90°,∴∠D=90°﹣∠COD=20°.
12.52
【解析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.
根据圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,
∴AB+BC+CD+AD=52故填:52
13.相切或相交.
【解析】根据直线与圆的位置关系来判定.判断直线和圆的位置关系:①直线l和⊙O相交?d<r;②直线l和⊙O相切?d=r;③直线l和⊙O相离?d>r.分OP垂直于直线l,OP不垂直直线l两种情况讨论.
当OP垂直于直线l时,即圆心O到直线l的距离d=2=r,⊙O与l相切;
当OP不垂直于直线l时,即圆心O到直线l的距离d<2=r,⊙O与直线l相交.
故直线l与⊙O的位置关系是相切或相交.
14.相交
【解析】本题可根据方程解出两个半径的值,将两个半径的和或差与圆心距比较,若d>R+r则两圆相离,若d=R+r则两圆外切,若d=R﹣r则两圆内切,若R﹣r<d<R+r则两圆相交.本题可把半径的值代入,看符合哪一种情况.
解:解方程(x﹣1)(x﹣2)=0,得x1=1,x2=2,
∵2﹣1=1<2<2+1=3,所以两圆相交.
15.4.
【解析】分两圆内切和两圆外切两种情况讨论即可得到⊙P的个数.
如图,
满足条件的⊙P有4个.
16.1或2.
【解析】∵由题意,圆P与这两个圆都相切,∴两种情形:
若圆P与两圆均外切,如答图1所示,此时圆P的半径=(3﹣1)=1cm;
若圆P与两圆均内切,如答图2所示,此时圆P的半径=(3+1)=2cm.
综上所述,圆P的半径为1cm或2cm.
17.(1)见解析 (2)- (3)5
【解析】(1)连接OD、OE,根据∠ADO+∠DBA=90°以及∠∠CDA=∠CBD得出∠ODC=90°;(2)阴影部分的面积等于△OCD的面积减去扇形ODA的面积进行计算;(3)将∠CDA转化成∠OEB,然后利用勾股定理进行求解.【来源:21cnj*y.co*m】
解:(1)证明:连OD,OE,∵AB为直径,∴∠ADB=90°,即∠ADO+∠BDO=90°,
又∵∠CDA=∠CBD,而∠CBD=∠BDO,∴∠BDO=∠CDA,∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
∵OD=1,∠CBD=30° ∴∠DOC=60° ∴∠C=30° ∴OC=2,CD=
∴△OCD的面积= 扇形ODA的面积= ∴阴影部分的面积=-;
(3)∵EB为⊙O的切线,∴ED=EB,OE⊥DB,∴∠ABD+∠DBE=90°,
∠OEB+∠DBE=90°,∴∠ABD=∠OEB,∴∠CDA=∠OEB.而tan∠CDA=,
∴tan∠OEB==,∵Rt△CDO∽Rt△CBE,∴,∴CD=×12=8,
在Rt△CBE中,设BE=x,∴(x+8)2=x2+122,解得x=5.即BE的长为5.
18.见解析
【解析】(1)连接OD,根据EF切⊙O于点D,可得OD⊥EF,又BH⊥EF,所以OD∥BH,然后证明∠ODB=∠OBD=∠DBH即可;(2)过点O作OG⊥BC于点G,由垂径定理和勾股定理可求出圆心O到BC的距离.
解:(1)证明:连接OD.
∵EF是⊙O的切线,∴OD⊥EF.
又∵BH⊥EF,∴OD∥BH,∴∠ODB=∠DBH.
而OD=OB,∴∠ODB=∠OBD,∴∠OBD=∠DBH,∴BD平分∠ABH.
(2)过点O作OG⊥BC于点G,则BG=CG=4,
在Rt△OBG中,OG=.
19.(1)证明见解析;(2)2-.
【解析】 (1)首先过点A作AF⊥ON于点F,易证得AF=AB,即可得ON是⊙A的切线;
(2)由∠MON=60°,AB⊥OM,可求得AF的长,又由S阴影=S△AEF-S扇形ADF,即可求得答案.www.21-cn-jy.com
解:(1)证明:过点A作AF⊥ON于点F,
∵⊙A与OM相切于点B,∴AB⊥OM,
∵OC平分∠MON,∴AF=AB=2,∴ON是⊙A的切线;
(2)解:∵∠MON=60°,AB⊥OM,∴∠OEB=30°,∴AF⊥ON,∴∠FAE=60°,
在Rt△AEF中,tan∠FAE=,∴EF=AF?tan60°=2,
∴S阴影=S△AEF-S扇形ADF=AF?EF-×π×AF2=2-.
20.见解析
【解析】(1)连结OD,根据条件证明即可;(2)根据条件可得BC=2DE=4,Rt△ABC中,先由∠BAC=30°,得AC=2 BC =8,再根据条件可证△EDC为等边三角形,可得出DC=2, AD=AC-CD=6.
解:(1)证明:连接OD,OE,
∵AB为圆O的直径,∴∠ADB=∠BDC=90°,在Rt△BDC中,E为斜边BC的中点,∴DE=BE,
在△OBE和△ODE中,OB=OD,OE=OE,BE=DE,∴△OBE≌△ODE(SSS),∴∠ODE=∠ABC=90°,所以DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,∴BC= AC,∵BC=2DE=4,∴AC=8,又∵∠C=60°,DE=DC,∴△DEC为等边三角形,即DC=DE=2,所以AD=AC-DC=6.
21.(1)见解析(5分) (2)见解析(5分)
【解析】(1)连接OC,可证明四边形ODCE是矩形,所以DE=OC=r,又DM=2EM,所以DM=DE;(2)根据条件证明PC⊥OC即可.
解:(1)证明:连接OC,∵点C是上异于A、B的点,又CD⊥OA于点D,CE⊥OB于点E,∴∠ODC=∠OEC=∠AOB=90°,∴四边形ODCE是矩形,∴DE=OC.∵OC=OA=r,∴DE=r.又∵DM=2EM,∴DM=r;(2)证明:设OC与DE交于点F,则在矩形ODCE中,FC=FD,∴∠CDE=∠DCO,又∵∠CPD+∠PCD=90°,∠CPD=∠CDE,∴∠DCO+∠PCD=90°,即PC⊥OC于点C,又∵OC为扇形OAB的半径,∴PC是扇形OAB所在圆的切线.
22.(2) 直线CD是⊙P的切线, r=6
【解析】(1)连接OC,利用已知条件计算出CE和OB的长度,再证明△BCO为直角三角形,利用:直角三角形斜边上的中线等于斜边的一半即可证明OE=CE;
(2)①直线CD是⊙P的切线,证明PC⊥CD.②设⊙P的半径为r,则在Rt△PCD中,由勾股定理得到关于r的方程,求出r即可.
解:
证明:连结OC,
∵ 直线y=x+2与y轴相交于点E,∴点E的坐标为(0,2),即OE=2。
又∵点B的坐标为(0,4),∴OB=4,∴ BE=OE=2,
又∵OA是⊙P的直径,∴ ∠ACO=90o,即OC⊥AB,
∴OE=CE(直角三角形斜边上的中线等于斜边的一半).
(2)直线CD是⊙P的切线.
证明:连结PC、PE,由①可知:OE=CE.
在△POE和△PCE,∴ △POE≌△PCE,∴∠POE=∠PCE.
又∵x轴⊥y轴,∴∠POE=∠PCE=90o,∴PC⊥CE,即:PC⊥CD。
又∵直线CD经过半径PC的外端点C,∴直线CD是⊙P的切线。
∵ 对,
当y=0时,,即OD=6,
在Rt△DOE中,,
∴ CD=DE+EC=DE+OE=。
设⊙P的半径为r,则在Rt△PCD中,由勾股定理知PC2+CD2=PD2,即r2+()2=(6+r)2,
解得r=6,即⊙P的半径长为6。
23.(1)30°;(2)18°.
【解析】(1)如图①,首先连接OC,根据当直线l与⊙O相切于点C,AD⊥l于点D.易证得OC∥AD,继而可求得∠BAC=∠DAC=30°;21cnjy.com
(2)如图②,连接BF,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠AFB=90°,由三角形外角的性质,可求得∠AEF的度数,又由圆的内接四边形的性质,求得∠B的度数,继而求得答案. 21*cnjy*com
