5.3一元一次不等式（一）

课件12张PPT。5.3一元一次不等式（一）
不等式的性质1：
若a不等式的性质2：
如果a>b，那么a+c>b+c;
如果a不等式的性质3：
如果a>b，并且c>0，那么ac>bc。
如果a>b，并且c<0，那么ac4 ；
（3）3x=30； （4）3x>30
（5）1.5x+12=0.5x+1；（6）1.5x+12<0.5x+1 ；
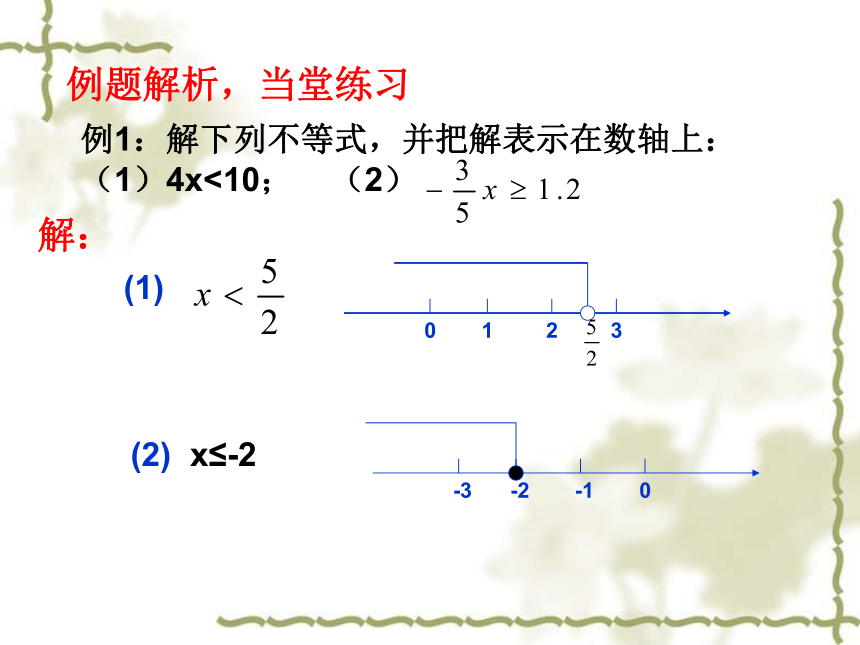
（7） ； （8）不等号的左右两边都是_______，而且只含有_______未知数，未知数的最高次数是_______，这样的不等式叫做一元一次不等式。整式一个一次左边的式子与右边的式子相比较，你能找出哪些相同点与不同点？例题解析，当堂练习例1：解下列不等式，并把解表示在数轴上：
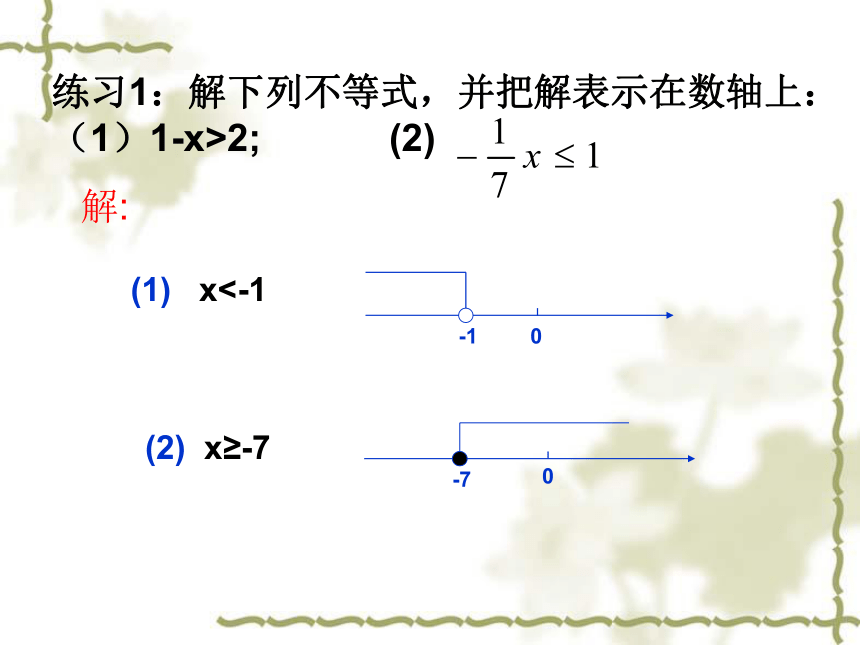
（1）4x<10； （2）练习1：解下列不等式，并把解表示在数轴上：
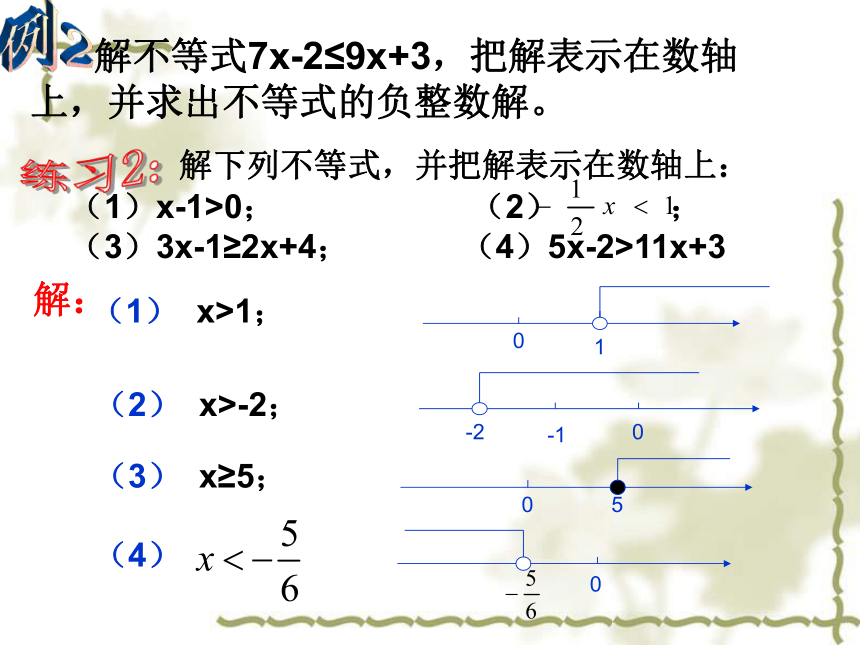
（1）1-x>2; (2) 根据数轴上表示的不等式的解，写出不等式的特殊解：练习3：自然数解：________负整数解：______最小的正整数解：______0，1，2-11 某种光盘的存储容量为670MB，一个文件平均占用空间为13MB，这张光盘能存放52个这样的文件吗？这张光盘最多能存放多少个这样的文件？解：∵52×13=676>670
∴这张光盘不能存放52个这样的文件。
设这张光盘上存放了x个文件，则
13x≤670
∴x的最大整数值为51。
∴这张光盘最多能存放51个这样的文件。

例3
一个等腰三角形的周长为10，设这个等腰三角形的腰长为x，则这个等腰三角形的底边长为________，根据底边为正数，可得关于x的不等式为_____________，解得x______。根据这个解，又若x为整数，x可取值为__________，把它们分别代入进去，根据构成三角形的三条线段之间的关系，可知这样的三角形共有______种不同的形状。
练习4：10-2x10-2x>0<51，2，3，42轻松过关1.下列不等式的解法正确吗？如果不正确，请改正。
（1）-2x<-4
解：两边同除以-2，得______。
（2）x+1>2x-3
解：移项，得4>x，即_______。
X<2X>4X>2X<42.写出两个解为x>8的一元一次不等式。适度拓展1.解不等式0.5x-3>-14-2.5x，把解表示在数轴上，
并求出适合不等式的最大负整数和最小正整数。最大负整数解x=-1，最小正整数解x=12.如果x=2是不等式（a-2）x<4a+2的一个解，试 求a的最小整数值。解：2（a-2）<4a+2
2a-4<4a+2
2a-4a<2+4
-2a<6 ∴a的最小整数值为-2。
a>-33.如果两个不等式3x>-6与（a+1）x>1的解集相同，
试求a的值。解：由3x>-6得x<-2
∵（a+1）x>1的解集为x<-2
∴
4.如果关于x 的不等式（a+1）x<2的自然数解有且只
有一个，试求a的取值范围。解：∵自然数解只有1个
∴原不等式的解不可能是x大于某一个数
∴a+1>0 得
∴又易知这个自然数必为0
∴ 而a+1≥0
∴ 2≤a+1 ∴a≥1 即a的取值范围是a>1。