浙教版数学2014-2015学年九下单元精品卷 第二章 直线与圆的位置关系(培优提高)含精析
文档属性
| 名称 | 浙教版数学2014-2015学年九下单元精品卷 第二章 直线与圆的位置关系(培优提高)含精析 |

|
|
| 格式 | zip | ||
| 文件大小 | 540.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-25 00:00:00 | ||
图片预览



文档简介
【浙教版】数学2014-2015学年九下“单元精品卷”(培优提高卷)
第二章 直线与圆的位置关系
题 号
仔细选一选
认真填一填
全面答一答
总 分
得 分
一、仔细选一选。(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内.注意可以用多种不同的方法来选取正确答案.
1.如图,两个半圆,大半圆中长为16cm的弦AB平行于直径CD,且与小半圆相切,则图中阴影部分的面积为( )
A.64π B.32π C.16π D.128π
2.如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是 ( )
①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为弧AD的中点.
A. ①②④ B.①③④ C. ①② D.②③
3.如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB 上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B. C.2 D.3
4.如图,在Rt△AOB中,OA=OB=,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A. B.2 C. D.
5.如图,PA、PB分别切⊙O于A、B,圆周角AMB=,EF切⊙O于C,交PA、PB于E、F,PEF的外心在PE上,PA=3.则AE的长为( )
A. B. C. 1 D.
6.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm B.15cm C.10cm D.随直线MN的变化而变化
7.已知如图,直角三角形纸片中,∠C=90°,AC=6,BC=8,若要在纸片中剪出两个相外切的等圆,则圆的半径最大为( )
A. B. C.1 D.
8.如果A、B分别是圆O1、圆O2上两个动点,当A、B两点之间距离最大时,那么这个最大距离被称为圆O1、圆O2的“远距”.已知,圆O1的半径为1,圆O2的半径为2,当两圆相交时,圆O1、圆O2的“远距”可能是( )
(A)3 (B)4 (C)5 (D)6.
9.己知⊙O1和⊙O2的半径分别为1和3,从如图所示位置(⊙O1与⊙O2内切)开始,将⊙O1向右平移到与⊙O2外切止,那么在这个运动过程中(包括起始位置与终止位置),圆心距O1O2的取值范围在数轴上表示正确的是( )
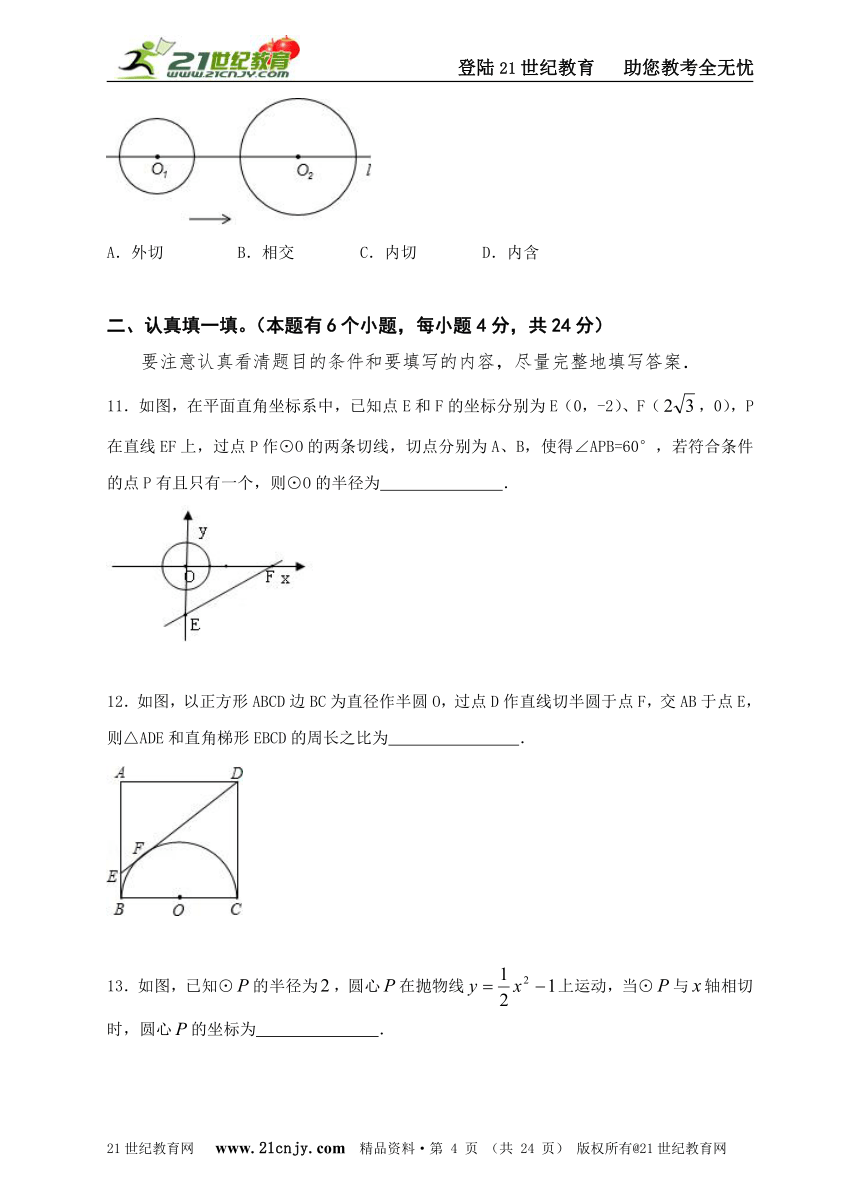
10.如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1m/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是( )
A.外切 B.相交 C.内切 D.内含
二、认真填一填。(本题有6个小题,每小题4分,共24分)
要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.
11.如图,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(,0),P在直线EF上,过点P作⊙O的两条切线,切点分别为A、B,使得∠APB=60°,若符合条件的点P有且只有一个,则⊙O的半径为 .
12.如图,以正方形ABCD边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,则△ADE和直角梯形EBCD的周长之比为 .
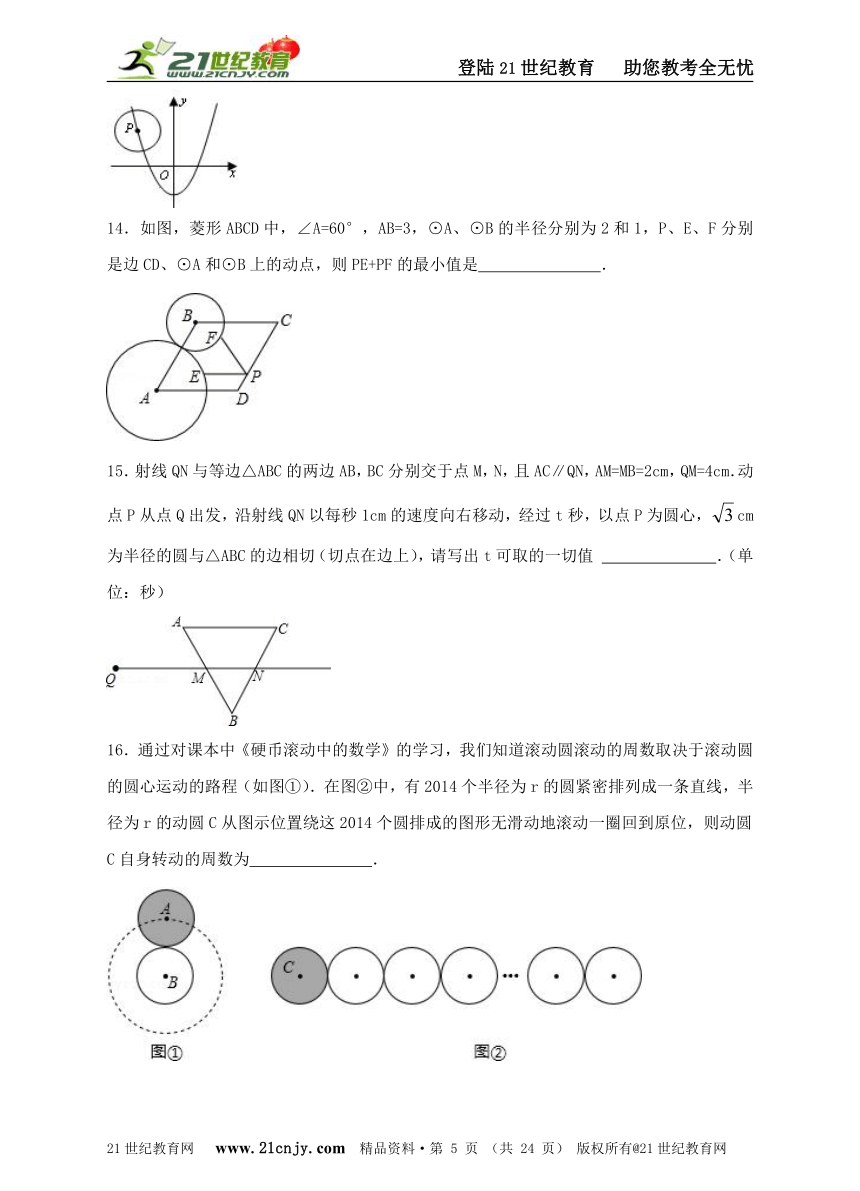
13.如图,已知⊙的半径为,圆心在抛物线上运动,当⊙与轴相切时,圆心的坐标为 .
14.如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最小值是 .
15.射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 .(单位:秒)
16.通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为 .
三、全面答一答。(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.
17.在△ABC中,∠BAC=90°,,AB=AC=,圆的半径为1,如图所示,若点O在BC边上运动(与点B、C不重合),设OB=x,△AOC的面积为y.
(1)求y关于x的函数解析式,并写出自变量的取值范围;
(2)以点O为圆心,BO长为半径作圆,求当圆O与圆A相切时,△AOC的面积.
18.如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交轴于D点,过点D作DF⊥AE于点F
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)直线BC上存不存在除点E以外的点P,使△AOP也是等腰三角形,如果不存在,说明理由;如果存在,直接写出P点的坐标.
19.以原点为圆心,为半径的圆分别交、轴的正半轴于A、B两点,点P的坐标为.
(1)如图一,动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设经过的时间为秒,当时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留);
(2)若点Q按照⑴中的方向和速度继续运动,
①当为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.
20.如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为1cm,矩形ABCD的边AD、AB分别与l1,l2重合,AB=cm,AD=2cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为2cm/s,矩形ABCD的移动速度为3cm/s,设移动时间为t(s).
(1)如图①,连接OA、AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<1时,求t的取值范围(解答时可以利用备用图画出相关示意图).
21.在平面直角坐标系中,点M(,),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与轴、轴的另一交点分别为点D、A(如图),连接AM.点P是上的动点.
(1)∠AOB的度数为 .
(2)Q是射线OP上的点,过点Q作QC垂直于直线OM,垂足为C,直线QC交轴于点E.
①当QE与⊙M相切时,求点E的坐标;
②在①的条件下,在点P运动的整个过程中,求△ODQ面积的最大值及点Q经过的路径长.
22.如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若tan∠ADB=,PA=AH,求BD的长;
(3)在(2)的条件下,求四边形ABCD的面积.
23.如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
参考答案与详解
1.B
【解析】设两个半圆的半径分别是R,r,因为大半圆中长为16cm的弦AB平行于直径CD,且与小半圆相切,所以大圆圆心到弦AB的距离是r,由垂径定理和勾股定理得:,图中阴影部分的面积=大半圆的面积-小半圆的面积= ,故选:B.
2.C
3.B
【解析】如图,过点O作OP1⊥AB,过点P1作⊙O的切线交⊙O于点Q1,连接OQ,OQ1.
当PQ⊥AB时,易得四边形P1PQO是矩形,即PQ=P1O.
∵P1Q1是⊙O的切线, ∴∠OQ1P1=900.∴在Rt△OP1Q1中,P1Q1<P1O,
∴P1Q1即是切线长PQ的最小值.
∵A(-4,0),B(0,4),∴OA=OB=4.∴△OAB是等腰直角三角形.
∴△AOP1是等腰直角三角形.根据勾股定理,得OP1=.
∵⊙O的半径为1,∴OQ1=1.
根据勾股定理,得P1Q1==.故选B.
4.C.
【解析】连接OP、OQ.
∵PQ是⊙O的切线,∴OQ⊥PQ;
根据勾股定理知,∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=,∴AB=OA=6,∴OP==3,
∴PQ=.故选C.
5.B
【解析】连接OA,OB,
∵PA,PB分别切⊙O于A、B,∴OA⊥PA,OB⊥PB,PA=PB=3,
∵∠AMB=60°,∴∠AOB=2∠AMB=120°,∴∠P=180°﹣∠AOB=60°,
∵EF切⊙O于C,∴EA=EC,FC=FB,
∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF=PE+AE+BF+PF=PA+PB=6,
∵△PEF的外心在PE上,∴PE是△PEF的外接圆的直径,∴∠PFE=90°,
设PF=x,则PE=2x,EF=x,∴x+2x+x=6,解得:x=3﹣,∴PE=6﹣2,
∴AE=PA﹣PE=3﹣(6﹣2)=2﹣3.故选D.
6.A
【解析】由题意可知,MD=ME,NF=NE,所以△AMN的周长为AM+ME+NE+AN=2AD=20㎝.
7.B.
【解析】设圆的半径是r,将两圆圆心与已知的点连接.
∴根据勾股定理求得AB=10,∴斜边上的高是:6×8÷10=4.8,
∴S△AMC+S△CNB+S△CMN+S梯形MABN
∴3r+4r+×2r+=×6×8,解得:r=.故选:B.
8.C.
【解析】
∵⊙O1的半径为1,⊙O2的半径为2,∴圆心距d的取值范围为:1<d<3,
∴⊙O1、⊙O2的“远距”的取值范围为:4<远距<6,故选C.
9.A
【解析】当两圆外切时,圆心距d=3+1=4,两圆外切时,圆心距d=3-1=2,∴在这个运动过程中(包括起始位置与终止位置),圆心距O1O2的取值范围是2≤d≤4,故选A.
考点:圆与圆的位置关系;在数轴上表示不等式的解集.
10.D
【解析】∵O1O2=8cm,⊙O1以1m/s的速度沿直线l向右运动,7s后停止运动,
∴7s后两圆的圆心距为:1cm,
此时两圆的半径的差为:3﹣2=1cm,∴此时内切,∴移动过程中没有内含这种位置关系,
故选D.
11.
【解析】由题意可知∠APB=60°,∠OBP=90°,所以∠BP0=30°,因此PO=2OB;又因符合条件的点P有且只有一个,所以OP⊥EF;再由E、F的坐标可求得EF=,再根据三角形的面积可知,即可求得OB=.
12.6∶7.
【解析】根据切线长定理得,BE=EF,DF=DC=AD=AB=BC.设EF=x,DF=y,
则在直角△AED中,AE=y﹣x,AD=CD=y,DE=x+y.
根据勾股定理可得:,∴,∴三角形ADE的周长为12x,直角梯形EBCD周长为14x,∴两者周长之比为12x:14x=6:7,故△ADE和直角梯形EBCD周长之比为6:7.
13.(,2)或(-,2).
【解析】当⊙P与x轴相切时,P点的纵坐标为2,可将其代入抛物线的解析式中,即可求得P点坐标.
解:当⊙P与x轴相切时,P点纵坐标为±2;
当y=2时,x2-1=2,解得x=±;
当y=-2时,x2-1=-2,x无解;故P点坐标为(,2)或(-,2).
14.3.
【解析】由题意可得出:当P与D重合时,E点在AD上,F在BD上,此时PE+PF最小,
如答图,连接BD,
∵菱形ABCD中,∠A=60°,∴AB=AD.∴△ABD是等边三角形.∴BD=AB=AD=3.
∵⊙A、⊙B的半径分别为2和1,∴PE=1,DF=2.∴PE+PF的最小值是3.
15.t=2或3≤t≤7或t=8.
【解析】∵△ABC是等边三角形,∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,
∵QN∥AC,AM=BM.∴N为BC中点,∴MN=AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
分为三种情况:①如图1,
当⊙P切AB于M′时,连接PM′,则PM′=cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,∴QP=4cm﹣2cm=2cm,即t=2;
②如图2,
当⊙P于AC切于A点时,连接PA,则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=cm,
∴PM=1cm,∴QP=4cm﹣1cm=3cm,
即t=3,
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=cm,∴P′N=1cm,
∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切;
③如图3,
当⊙P切BC于N′时,连接PN′,则PN′=cm,∠PN′N=90°,
∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm,∴QP=4cm+2cm+2cm=8cm,即t=8;
故答案为:t=2或3≤t≤7或t=8.
16.1314.
【解析】它从A位置开始,滚过与它相同的其他2014个圆的上部,到达最后位置.则该圆共滚过了2014段弧长,其中有2段是半径为2r,圆心角为120度,2012段是半径为2r,圆心角为60度的弧长,所以可求得动圆C自身转动的周数为: 1314.故答案是1314.
17.(1)y= -x+4(0【解析】(1)过点A作AD⊥BC于点D,S△AOC=OC×AD=×2×(4-x)= 4-x ;
(2)圆O与圆A相切,分外切和内切两种情况讨论:,在Rt△AOD中,根据AO2=AD2+OD2= 4+(2-x)2=x2-4x+8,求出x的值,可求.
解:(1)过点A作AD⊥BC于点D
∵∠BAC=90° AB=AB=2 ∴BC= 4 AD=BC=2∴S△AOC=OC×AD=×2×(4-x)= 4-x
即y= -x+4(0(2)当点O与点D重合时,圆O与圆A相交,不合题意
当点O与点D不重合时,在Rt△AOD中,
AO2=AD2+OD2= 4+(2-x)2=x2-4x+8
∵⊙O1的半径是1,⊙O2的半径是x∴①当⊙A与⊙O外切时
(x+1)2=x2-4x+8 解得x= 此时,△AOC的面积是y= 4-=
②当⊙A与⊙O内切时(x+1)2=x2-4x+8 解得x=此时,△AOC的面积是y= 4-=
∴当⊙A与⊙O相切时,△AOC的面积为或。
18.(1)OC=3, OA=5;(2)证明见试题解析;(3)存在, P1(1,3) P4(9,3) P2(4,3),P3(4,3).
【解析】(1)根据矩形面积公式得方程求解;
(2)由E是BC中点,OC=AB,∠C=∠B可证△ABE≌△OCE,则OE=AE得证;
(3)连接O′D,证∠O′DF=90°.
(4)分别以∠AOP、∠OAP为顶角讨论P点位置求解.
解:(1)设OC=x,则OA=x+2,根据题意得:x(x+2)=15.解得x=3,即OC=3.则OA=5.
(2)∵E为BC的中点,∴CE=BE.又OC=AB,∠OCE=∠B=90°,∴△ABE≌△OCE,∴OE=AE.
(3)连接O′D.
∵OE=AE,O′O=O′D,∴∠EOD=∠EAO=∠O′DO.
∵DF⊥AE,∴∠EAO+∠ADF=90°.∴∠O′DO+∠ADF=90°.∴∠O′DF=90°,DF是⊙O′的切线;
(4)存在.如图所示.
①当AP=AO时,BP=4,则CP=1或9,所以P(1,3)或(9,3);
②当OP=OA时,CP=4,所以P(4,3)或(-4,3).
19.(1)点Q的运动速度为;(2)1;(3) cm.
【解析】(1)连接OQ,求出∠QPO,求出∠BOQ,根据弧长公式求出即可;
(2)分为四种情况,画出图形,求出弧长,即可求出答案;
解:(1)如图1,连接OQ,则OQ⊥PQ.
∵OQ=OA=1,OP=2,∴∠QPO=30°,
∵∠PQO=90°,∴∠QOP=60°,∴∠BOQ=30°,∴弧BQ的长是,
∵运动时间t=1,∴点Q的运动速度为;
(2)分为四种情况:①由(1)可知,当t=1时,△OPQ为直角三角形;
②如图3,当t=6或t=12时,直线PQ与⊙O相交,设交点为N,
作OM⊥PQ,根据等面积法可知:PQ?OM=OQ?OP,
PQ=,OM=,QM=,弦长QN=2QM=cm.
20.(1)105°;(2);(3).
【解析】(1)利用切线的性质以及锐角三角函数关系分别求出∠OAD=45°,∠DAC=60°,进而得出答案;
(2)首先得出,∠C1A1D1=60°,再利用A1E=AA1﹣OO1﹣1=t﹣1,求出t的值,进而得出OO1=2t得出答案即可;
(3)①当直线AC与⊙O第一次相切时,设移动时间为t1,②当直线AC与⊙O第二次相切时,设移动时间为t2,分别求出即可.
解:(1)∵l1⊥l2,⊙O与l1,l2都相切,∴∠OAD=45°,
∵AB=cm,AD=4cm,∴CD=cm,AD=4cm,∴tan∠DAC=,∴∠DAC=60°,∴∠OAC的度数为:∠OAD+∠DAC=105°,
故答案为:105;
②当直线AC与⊙O第二次相切时,设移动时间为t2,,解得:,
∵d<1时,对角线AC所在直线与⊙O相交,∴t的取值范围是:.
21.(1)45°;(2)①E点坐标为(,0);②△ODQ面积的最大值为8,Q经过的路径长为4.
【解析】(1)首先过点M作MH⊥OD于点H,由点M(,),可得∠MOH=45°,OH=MH=,继而求得∠AOM=45°;
(2)①由OH=MH=,MH⊥OD,即可求得OD与OM的值,继而可得OB的长,由于QE与⊙M相切,所以B与C重合,故△OBE为等腰直角三角形,从而得到OE=OB=,得到点E的坐标;
②由OD=,Q的纵坐标为t,即可得S=,当动点P与A点重合时,Q点与y轴上R点重合,此时Q点的纵坐标最大,可求得OQ的长,继而求得△ODQ的最大面积;由已知可得:Q在线段BR上运动,显然BR=OB=4.
解:(1)过点M作MH⊥OD于点H,
∵点M(,),∴OH=MH=,∴∠MOD=45°,∵∠AOD=90°,∴∠AOM=45°;
(2)①∵OH=MH=,MH⊥OD,
∴OM==2,OD=2OH=,∴OB=4,
∵QE与⊙M相切,∴B与C重合,∴△OBE为等腰直角三角形,∴OE=OB=,
∴E点坐标为(,0)
②∵OD=,Q的纵坐标为t,∴S=.
如图2,当动点P与A点重合时,Q点与y轴上R点重合,此时Q点的纵坐标最大,
∵∠AOM=45°,OB=4,∠OBR=90°,∴BR=OB=4,∴OR=,∴,
∴.
∵Q只能在线段BR上运动.∴Q经过的路径长为BR=4.
22.(1)PD与圆O相切;理由见解析;(2)25;(3)900+.
【解析】(1)首先连接DO并延长交圆于点E,连接AE,由DE是直径,可得∠DAE的度数,又由∠PDA=∠ABD=∠E,可证得PD⊥DO,即可得PD与圆O相切于点D;
(2)首先由tan∠ADB=,可设AH=3k,则DH=4k,又由PA=AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE?cos30°=25;
(3)由(2)易得HC=(25-4k),又由PD2=PA×PC,可得方程:(8k)2=(4-3)k×[4k+(25-4k)],解此方程即可求得AC的长,继而求得四边形ABCD的面积.
解:(1)PD与圆O相切.
理由:如图,连接DO并延长交圆于点E,连接AE,
∵DE是直径,∴∠DAE=90°,∴∠AED+∠ADE=90°,
∵∠PDA=∠ABD=∠AED,∴∠PDA+∠ADE=90°,即PD⊥DO,∴PD与圆O相切于点D;
(2)∵tan∠ADB=∴可设AH=3k,则DH=4k,
∵PA=AH,∴PA=()k,∴PH=4k,
∴在Rt△PDH中,tan∠P=,∴∠P=30°,∠PDH=60°,
∵PD⊥DO,∴∠BDE=90°-∠PDH=30°,连接BE,则∠DBE=90°,DE=2r=50,
∴BD=DE?cos30°=25;
(3)由(2)知,BH=25-4k,∴HC=,
又∵PD2=PA×PC,∴(8k)2=(4-3)k×[4k+],
解得:k=4-3,∴AC=3k+=24+7,
∴S四边形ABCD=BD?AC=×25×(24+7)=900+.
23.(1).(2)0°≤α≤60°.(3)
【解析】(1)连接OA,如下图1,根据条件可求出AB,然后AC的高BH,求出BH就可以求出△ABC的面积.
(2)如下图2,首先考虑临界位置:当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;当线段AB所在的直线与圆O相切时,线段AB与圆O只有一个公共点,此时α=60°.从而定出α的范围.
(3)设AO与PM的交点为D,连接MQ,如下图3,易证AO∥MQ,从而得到△PDO∽△PMQ,△BMQ∽△BAO,又PO=OQ=BQ,从而可以求出MQ、OD,进而求出PD、DM、AM、CM的值.
解:(1)连接OA,过点B作BH⊥AC,垂足为H,如图1所示.
∵AB与⊙O相切于点A,∴OA⊥AB.∴∠OAB=90°.
∵OQ=QB=1,∴OA=1.∴AB=.
∵△ABC是等边三角形,∴AC=AB=,∠CAB=60°.
∵sin∠HAB=,∴HB=AB?sin∠HAB=.∴S△ABC=AC?BH=.
∴△ABC的面积为.
(2)①当点A与点Q重合时,
线段AB与圆O只有一个公共点,此时α=0°;
②当线段A1B所在的直线与圆O相切时,如图2所示,
线段A1B与圆O只有一个公共点,此时OA1⊥BA1,OA1=1,OB=2,∴cos∠A1OB=.
∴∠A1OB=60°.∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.
(3)连接MQ,如图3所示.
∵PQ是⊙O的直径,∴∠PMQ=90°.
∵OA⊥PM,∴∠PDO=90°.∴∠PDO=∠PMQ.∴△PDO∽△PMQ.∴
第二章 直线与圆的位置关系
题 号
仔细选一选
认真填一填
全面答一答
总 分
得 分
一、仔细选一选。(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内.注意可以用多种不同的方法来选取正确答案.
1.如图,两个半圆,大半圆中长为16cm的弦AB平行于直径CD,且与小半圆相切,则图中阴影部分的面积为( )
A.64π B.32π C.16π D.128π
2.如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是 ( )
①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为弧AD的中点.
A. ①②④ B.①③④ C. ①② D.②③
3.如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB 上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B. C.2 D.3
4.如图,在Rt△AOB中,OA=OB=,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A. B.2 C. D.
5.如图,PA、PB分别切⊙O于A、B,圆周角AMB=,EF切⊙O于C,交PA、PB于E、F,PEF的外心在PE上,PA=3.则AE的长为( )
A. B. C. 1 D.
6.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm B.15cm C.10cm D.随直线MN的变化而变化
7.已知如图,直角三角形纸片中,∠C=90°,AC=6,BC=8,若要在纸片中剪出两个相外切的等圆,则圆的半径最大为( )
A. B. C.1 D.
8.如果A、B分别是圆O1、圆O2上两个动点,当A、B两点之间距离最大时,那么这个最大距离被称为圆O1、圆O2的“远距”.已知,圆O1的半径为1,圆O2的半径为2,当两圆相交时,圆O1、圆O2的“远距”可能是( )
(A)3 (B)4 (C)5 (D)6.
9.己知⊙O1和⊙O2的半径分别为1和3,从如图所示位置(⊙O1与⊙O2内切)开始,将⊙O1向右平移到与⊙O2外切止,那么在这个运动过程中(包括起始位置与终止位置),圆心距O1O2的取值范围在数轴上表示正确的是( )
10.如图,⊙O1,⊙O2的圆心在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm.O1O2=8cm,⊙O1以1m/s的速度沿直线l向右运动,7s后停止运动.在此过程中,⊙O1和⊙O2没有出现的位置关系是( )
A.外切 B.相交 C.内切 D.内含
二、认真填一填。(本题有6个小题,每小题4分,共24分)
要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.
11.如图,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(,0),P在直线EF上,过点P作⊙O的两条切线,切点分别为A、B,使得∠APB=60°,若符合条件的点P有且只有一个,则⊙O的半径为 .
12.如图,以正方形ABCD边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,则△ADE和直角梯形EBCD的周长之比为 .
13.如图,已知⊙的半径为,圆心在抛物线上运动,当⊙与轴相切时,圆心的坐标为 .
14.如图,菱形ABCD中,∠A=60°,AB=3,⊙A、⊙B的半径分别为2和1,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最小值是 .
15.射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 .(单位:秒)
16.通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为 .
三、全面答一答。(本题有7个小题,共66分)
解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.
17.在△ABC中,∠BAC=90°,,AB=AC=,圆的半径为1,如图所示,若点O在BC边上运动(与点B、C不重合),设OB=x,△AOC的面积为y.
(1)求y关于x的函数解析式,并写出自变量的取值范围;
(2)以点O为圆心,BO长为半径作圆,求当圆O与圆A相切时,△AOC的面积.
18.如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交轴于D点,过点D作DF⊥AE于点F
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)直线BC上存不存在除点E以外的点P,使△AOP也是等腰三角形,如果不存在,说明理由;如果存在,直接写出P点的坐标.
19.以原点为圆心,为半径的圆分别交、轴的正半轴于A、B两点,点P的坐标为.
(1)如图一,动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设经过的时间为秒,当时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留);
(2)若点Q按照⑴中的方向和速度继续运动,
①当为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.
20.如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为1cm,矩形ABCD的边AD、AB分别与l1,l2重合,AB=cm,AD=2cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为2cm/s,矩形ABCD的移动速度为3cm/s,设移动时间为t(s).
(1)如图①,连接OA、AC,则∠OAC的度数为 °;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<1时,求t的取值范围(解答时可以利用备用图画出相关示意图).
21.在平面直角坐标系中,点M(,),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与轴、轴的另一交点分别为点D、A(如图),连接AM.点P是上的动点.
(1)∠AOB的度数为 .
(2)Q是射线OP上的点,过点Q作QC垂直于直线OM,垂足为C,直线QC交轴于点E.
①当QE与⊙M相切时,求点E的坐标;
②在①的条件下,在点P运动的整个过程中,求△ODQ面积的最大值及点Q经过的路径长.
22.如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若tan∠ADB=,PA=AH,求BD的长;
(3)在(2)的条件下,求四边形ABCD的面积.
23.如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).
参考答案与详解
1.B
【解析】设两个半圆的半径分别是R,r,因为大半圆中长为16cm的弦AB平行于直径CD,且与小半圆相切,所以大圆圆心到弦AB的距离是r,由垂径定理和勾股定理得:,图中阴影部分的面积=大半圆的面积-小半圆的面积= ,故选:B.
2.C
3.B
【解析】如图,过点O作OP1⊥AB,过点P1作⊙O的切线交⊙O于点Q1,连接OQ,OQ1.
当PQ⊥AB时,易得四边形P1PQO是矩形,即PQ=P1O.
∵P1Q1是⊙O的切线, ∴∠OQ1P1=900.∴在Rt△OP1Q1中,P1Q1<P1O,
∴P1Q1即是切线长PQ的最小值.
∵A(-4,0),B(0,4),∴OA=OB=4.∴△OAB是等腰直角三角形.
∴△AOP1是等腰直角三角形.根据勾股定理,得OP1=.
∵⊙O的半径为1,∴OQ1=1.
根据勾股定理,得P1Q1==.故选B.
4.C.
【解析】连接OP、OQ.
∵PQ是⊙O的切线,∴OQ⊥PQ;
根据勾股定理知,∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=,∴AB=OA=6,∴OP==3,
∴PQ=.故选C.
5.B
【解析】连接OA,OB,
∵PA,PB分别切⊙O于A、B,∴OA⊥PA,OB⊥PB,PA=PB=3,
∵∠AMB=60°,∴∠AOB=2∠AMB=120°,∴∠P=180°﹣∠AOB=60°,
∵EF切⊙O于C,∴EA=EC,FC=FB,
∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF=PE+AE+BF+PF=PA+PB=6,
∵△PEF的外心在PE上,∴PE是△PEF的外接圆的直径,∴∠PFE=90°,
设PF=x,则PE=2x,EF=x,∴x+2x+x=6,解得:x=3﹣,∴PE=6﹣2,
∴AE=PA﹣PE=3﹣(6﹣2)=2﹣3.故选D.
6.A
【解析】由题意可知,MD=ME,NF=NE,所以△AMN的周长为AM+ME+NE+AN=2AD=20㎝.
7.B.
【解析】设圆的半径是r,将两圆圆心与已知的点连接.
∴根据勾股定理求得AB=10,∴斜边上的高是:6×8÷10=4.8,
∴S△AMC+S△CNB+S△CMN+S梯形MABN
∴3r+4r+×2r+=×6×8,解得:r=.故选:B.
8.C.
【解析】
∵⊙O1的半径为1,⊙O2的半径为2,∴圆心距d的取值范围为:1<d<3,
∴⊙O1、⊙O2的“远距”的取值范围为:4<远距<6,故选C.
9.A
【解析】当两圆外切时,圆心距d=3+1=4,两圆外切时,圆心距d=3-1=2,∴在这个运动过程中(包括起始位置与终止位置),圆心距O1O2的取值范围是2≤d≤4,故选A.
考点:圆与圆的位置关系;在数轴上表示不等式的解集.
10.D
【解析】∵O1O2=8cm,⊙O1以1m/s的速度沿直线l向右运动,7s后停止运动,
∴7s后两圆的圆心距为:1cm,
此时两圆的半径的差为:3﹣2=1cm,∴此时内切,∴移动过程中没有内含这种位置关系,
故选D.
11.
【解析】由题意可知∠APB=60°,∠OBP=90°,所以∠BP0=30°,因此PO=2OB;又因符合条件的点P有且只有一个,所以OP⊥EF;再由E、F的坐标可求得EF=,再根据三角形的面积可知,即可求得OB=.
12.6∶7.
【解析】根据切线长定理得,BE=EF,DF=DC=AD=AB=BC.设EF=x,DF=y,
则在直角△AED中,AE=y﹣x,AD=CD=y,DE=x+y.
根据勾股定理可得:,∴,∴三角形ADE的周长为12x,直角梯形EBCD周长为14x,∴两者周长之比为12x:14x=6:7,故△ADE和直角梯形EBCD周长之比为6:7.
13.(,2)或(-,2).
【解析】当⊙P与x轴相切时,P点的纵坐标为2,可将其代入抛物线的解析式中,即可求得P点坐标.
解:当⊙P与x轴相切时,P点纵坐标为±2;
当y=2时,x2-1=2,解得x=±;
当y=-2时,x2-1=-2,x无解;故P点坐标为(,2)或(-,2).
14.3.
【解析】由题意可得出:当P与D重合时,E点在AD上,F在BD上,此时PE+PF最小,
如答图,连接BD,
∵菱形ABCD中,∠A=60°,∴AB=AD.∴△ABD是等边三角形.∴BD=AB=AD=3.
∵⊙A、⊙B的半径分别为2和1,∴PE=1,DF=2.∴PE+PF的最小值是3.
15.t=2或3≤t≤7或t=8.
【解析】∵△ABC是等边三角形,∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,
∵QN∥AC,AM=BM.∴N为BC中点,∴MN=AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
分为三种情况:①如图1,
当⊙P切AB于M′时,连接PM′,则PM′=cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,∴QP=4cm﹣2cm=2cm,即t=2;
②如图2,
当⊙P于AC切于A点时,连接PA,则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=cm,
∴PM=1cm,∴QP=4cm﹣1cm=3cm,
即t=3,
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=cm,∴P′N=1cm,
∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切;
③如图3,
当⊙P切BC于N′时,连接PN′,则PN′=cm,∠PN′N=90°,
∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm,∴QP=4cm+2cm+2cm=8cm,即t=8;
故答案为:t=2或3≤t≤7或t=8.
16.1314.
【解析】它从A位置开始,滚过与它相同的其他2014个圆的上部,到达最后位置.则该圆共滚过了2014段弧长,其中有2段是半径为2r,圆心角为120度,2012段是半径为2r,圆心角为60度的弧长,所以可求得动圆C自身转动的周数为: 1314.故答案是1314.
17.(1)y= -x+4(0
(2)圆O与圆A相切,分外切和内切两种情况讨论:,在Rt△AOD中,根据AO2=AD2+OD2= 4+(2-x)2=x2-4x+8,求出x的值,可求.
解:(1)过点A作AD⊥BC于点D
∵∠BAC=90° AB=AB=2 ∴BC= 4 AD=BC=2∴S△AOC=OC×AD=×2×(4-x)= 4-x
即y= -x+4(0
当点O与点D不重合时,在Rt△AOD中,
AO2=AD2+OD2= 4+(2-x)2=x2-4x+8
∵⊙O1的半径是1,⊙O2的半径是x∴①当⊙A与⊙O外切时
(x+1)2=x2-4x+8 解得x= 此时,△AOC的面积是y= 4-=
②当⊙A与⊙O内切时(x+1)2=x2-4x+8 解得x=此时,△AOC的面积是y= 4-=
∴当⊙A与⊙O相切时,△AOC的面积为或。
18.(1)OC=3, OA=5;(2)证明见试题解析;(3)存在, P1(1,3) P4(9,3) P2(4,3),P3(4,3).
【解析】(1)根据矩形面积公式得方程求解;
(2)由E是BC中点,OC=AB,∠C=∠B可证△ABE≌△OCE,则OE=AE得证;
(3)连接O′D,证∠O′DF=90°.
(4)分别以∠AOP、∠OAP为顶角讨论P点位置求解.
解:(1)设OC=x,则OA=x+2,根据题意得:x(x+2)=15.解得x=3,即OC=3.则OA=5.
(2)∵E为BC的中点,∴CE=BE.又OC=AB,∠OCE=∠B=90°,∴△ABE≌△OCE,∴OE=AE.
(3)连接O′D.
∵OE=AE,O′O=O′D,∴∠EOD=∠EAO=∠O′DO.
∵DF⊥AE,∴∠EAO+∠ADF=90°.∴∠O′DO+∠ADF=90°.∴∠O′DF=90°,DF是⊙O′的切线;
(4)存在.如图所示.
①当AP=AO时,BP=4,则CP=1或9,所以P(1,3)或(9,3);
②当OP=OA时,CP=4,所以P(4,3)或(-4,3).
19.(1)点Q的运动速度为;(2)1;(3) cm.
【解析】(1)连接OQ,求出∠QPO,求出∠BOQ,根据弧长公式求出即可;
(2)分为四种情况,画出图形,求出弧长,即可求出答案;
解:(1)如图1,连接OQ,则OQ⊥PQ.
∵OQ=OA=1,OP=2,∴∠QPO=30°,
∵∠PQO=90°,∴∠QOP=60°,∴∠BOQ=30°,∴弧BQ的长是,
∵运动时间t=1,∴点Q的运动速度为;
(2)分为四种情况:①由(1)可知,当t=1时,△OPQ为直角三角形;
②如图3,当t=6或t=12时,直线PQ与⊙O相交,设交点为N,
作OM⊥PQ,根据等面积法可知:PQ?OM=OQ?OP,
PQ=,OM=,QM=,弦长QN=2QM=cm.
20.(1)105°;(2);(3).
【解析】(1)利用切线的性质以及锐角三角函数关系分别求出∠OAD=45°,∠DAC=60°,进而得出答案;
(2)首先得出,∠C1A1D1=60°,再利用A1E=AA1﹣OO1﹣1=t﹣1,求出t的值,进而得出OO1=2t得出答案即可;
(3)①当直线AC与⊙O第一次相切时,设移动时间为t1,②当直线AC与⊙O第二次相切时,设移动时间为t2,分别求出即可.
解:(1)∵l1⊥l2,⊙O与l1,l2都相切,∴∠OAD=45°,
∵AB=cm,AD=4cm,∴CD=cm,AD=4cm,∴tan∠DAC=,∴∠DAC=60°,∴∠OAC的度数为:∠OAD+∠DAC=105°,
故答案为:105;
②当直线AC与⊙O第二次相切时,设移动时间为t2,,解得:,
∵d<1时,对角线AC所在直线与⊙O相交,∴t的取值范围是:.
21.(1)45°;(2)①E点坐标为(,0);②△ODQ面积的最大值为8,Q经过的路径长为4.
【解析】(1)首先过点M作MH⊥OD于点H,由点M(,),可得∠MOH=45°,OH=MH=,继而求得∠AOM=45°;
(2)①由OH=MH=,MH⊥OD,即可求得OD与OM的值,继而可得OB的长,由于QE与⊙M相切,所以B与C重合,故△OBE为等腰直角三角形,从而得到OE=OB=,得到点E的坐标;
②由OD=,Q的纵坐标为t,即可得S=,当动点P与A点重合时,Q点与y轴上R点重合,此时Q点的纵坐标最大,可求得OQ的长,继而求得△ODQ的最大面积;由已知可得:Q在线段BR上运动,显然BR=OB=4.
解:(1)过点M作MH⊥OD于点H,
∵点M(,),∴OH=MH=,∴∠MOD=45°,∵∠AOD=90°,∴∠AOM=45°;
(2)①∵OH=MH=,MH⊥OD,
∴OM==2,OD=2OH=,∴OB=4,
∵QE与⊙M相切,∴B与C重合,∴△OBE为等腰直角三角形,∴OE=OB=,
∴E点坐标为(,0)
②∵OD=,Q的纵坐标为t,∴S=.
如图2,当动点P与A点重合时,Q点与y轴上R点重合,此时Q点的纵坐标最大,
∵∠AOM=45°,OB=4,∠OBR=90°,∴BR=OB=4,∴OR=,∴,
∴.
∵Q只能在线段BR上运动.∴Q经过的路径长为BR=4.
22.(1)PD与圆O相切;理由见解析;(2)25;(3)900+.
【解析】(1)首先连接DO并延长交圆于点E,连接AE,由DE是直径,可得∠DAE的度数,又由∠PDA=∠ABD=∠E,可证得PD⊥DO,即可得PD与圆O相切于点D;
(2)首先由tan∠ADB=,可设AH=3k,则DH=4k,又由PA=AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE?cos30°=25;
(3)由(2)易得HC=(25-4k),又由PD2=PA×PC,可得方程:(8k)2=(4-3)k×[4k+(25-4k)],解此方程即可求得AC的长,继而求得四边形ABCD的面积.
解:(1)PD与圆O相切.
理由:如图,连接DO并延长交圆于点E,连接AE,
∵DE是直径,∴∠DAE=90°,∴∠AED+∠ADE=90°,
∵∠PDA=∠ABD=∠AED,∴∠PDA+∠ADE=90°,即PD⊥DO,∴PD与圆O相切于点D;
(2)∵tan∠ADB=∴可设AH=3k,则DH=4k,
∵PA=AH,∴PA=()k,∴PH=4k,
∴在Rt△PDH中,tan∠P=,∴∠P=30°,∠PDH=60°,
∵PD⊥DO,∴∠BDE=90°-∠PDH=30°,连接BE,则∠DBE=90°,DE=2r=50,
∴BD=DE?cos30°=25;
(3)由(2)知,BH=25-4k,∴HC=,
又∵PD2=PA×PC,∴(8k)2=(4-3)k×[4k+],
解得:k=4-3,∴AC=3k+=24+7,
∴S四边形ABCD=BD?AC=×25×(24+7)=900+.
23.(1).(2)0°≤α≤60°.(3)
【解析】(1)连接OA,如下图1,根据条件可求出AB,然后AC的高BH,求出BH就可以求出△ABC的面积.
(2)如下图2,首先考虑临界位置:当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;当线段AB所在的直线与圆O相切时,线段AB与圆O只有一个公共点,此时α=60°.从而定出α的范围.
(3)设AO与PM的交点为D,连接MQ,如下图3,易证AO∥MQ,从而得到△PDO∽△PMQ,△BMQ∽△BAO,又PO=OQ=BQ,从而可以求出MQ、OD,进而求出PD、DM、AM、CM的值.
解:(1)连接OA,过点B作BH⊥AC,垂足为H,如图1所示.
∵AB与⊙O相切于点A,∴OA⊥AB.∴∠OAB=90°.
∵OQ=QB=1,∴OA=1.∴AB=.
∵△ABC是等边三角形,∴AC=AB=,∠CAB=60°.
∵sin∠HAB=,∴HB=AB?sin∠HAB=.∴S△ABC=AC?BH=.
∴△ABC的面积为.
(2)①当点A与点Q重合时,
线段AB与圆O只有一个公共点,此时α=0°;
②当线段A1B所在的直线与圆O相切时,如图2所示,
线段A1B与圆O只有一个公共点,此时OA1⊥BA1,OA1=1,OB=2,∴cos∠A1OB=.
∴∠A1OB=60°.∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.
(3)连接MQ,如图3所示.
∵PQ是⊙O的直径,∴∠PMQ=90°.
∵OA⊥PM,∴∠PDO=90°.∴∠PDO=∠PMQ.∴△PDO∽△PMQ.∴
