数据编码(上) - 进制与转换 课件(共22张PPT)
文档属性
| 名称 | 数据编码(上) - 进制与转换 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2023-10-11 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
数据编码
高中信息技术必修一 数据与信息
第一课时
课前回顾
数据:现实世界客观事物的符号记录。
(文字、图形、图像、音频、视频等。)
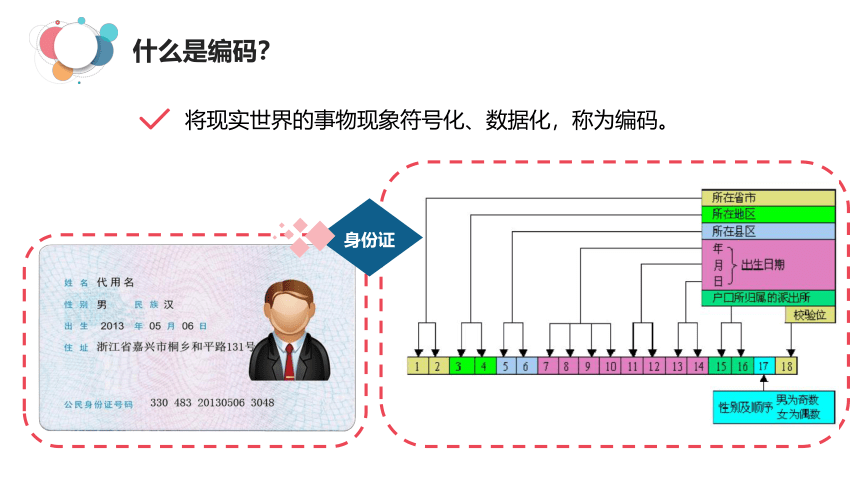
什么是数据?
身份证
什么是编码?
将现实世界的事物现象符号化、数据化,称为编码。
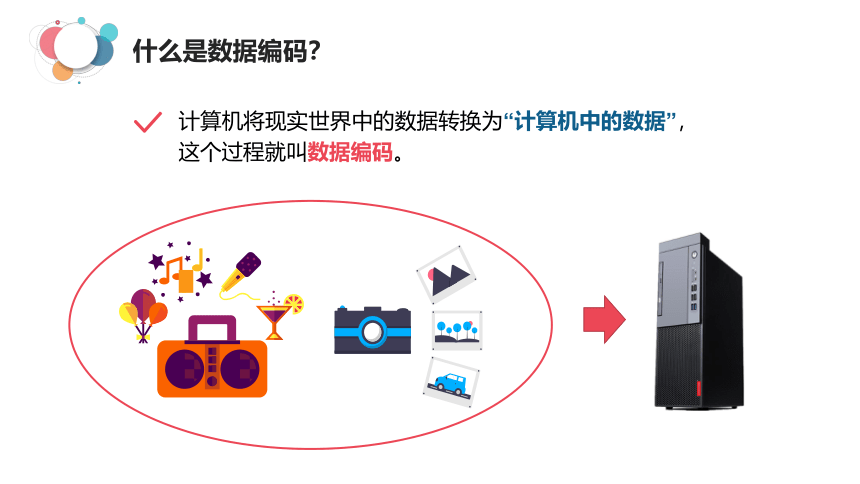
什么是数据编码?
计算机将现实世界中的数据转换为“计算机中的数据”,这个过程就叫数据编码。
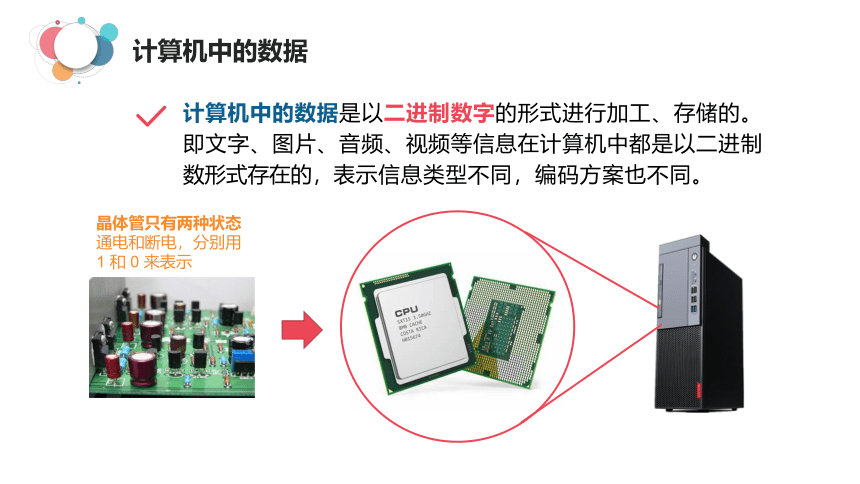
计算机中的数据是以二进制数字的形式进行加工、存储的。即文字、图片、音频、视频等信息在计算机中都是以二进制数形式存在的,表示信息类型不同,编码方案也不同。
晶体管只有两种状态
通电和断电,分别用 1 和 0 来表示
计算机中的数据
二进制数字是什么?和我们平时用的数字有什么不同?常见的数制有哪些呢?
进制与转换
02
生活中的进制
最常用的数制:十进制 —— 我们平时计算用的一般都是十进制,单个数位上最大数值为9,逢十进一。
1小时=60分钟,1分钟=60秒,用的是“六十进一”的计算方法。
1天=24小时,用的是“二十四进一”的计算方法。
“半斤八两”:古代1斤=16两,所以半斤和八两是一样多的,这里用的是十六进制。
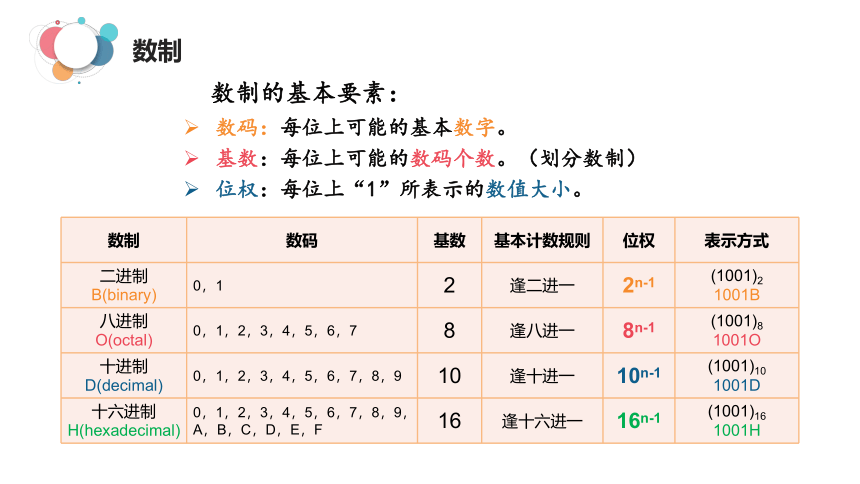
数制
数制的基本要素:
数码:每位上可能的基本数字。
基数:每位上可能的数码个数。(划分数制)
位权:每位上“1”所表示的数值大小。
数制 数码 基数 基本计数规则 位权 表示方式
二进制 B(binary) 0,1 2 逢二进一 2n-1 (1001)2
1001B
八进制 O(octal) 0,1,2,3,4,5,6,7 8 逢八进一 8n-1 (1001)8
1001O
十进制 D(decimal) 0,1,2,3,4,5,6,7,8,9 10 逢十进一 10n-1 (1001)10
1001D
十六进制 H(hexadecimal) 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 16 逢十六进一 16n-1 (1001)16
1001H
数字换算为十进制
数权相乘再相加
十进制数123: 1 2 3
位权:
1×102 + 2×101 + 3×100
102
100
101
10n-1
(123)10 =
原理讲解:
数字换算为十进制
数权相乘再相加
二进制数1101: 1 1 0 1
位权:
1×23 +1×22 +0×21 +1×20
22
20
21
23
2n-1
(13)10 =
实战演练:
进制转换练习
二进制:100B =
十六进制:100H =
1×22 + 0×21 + 0×20
= 4D
八进制:100O =
1×82 + 0×81 + 0×80
= 64D
1×162 + 0×161 + 0×160 = 256D
练习:不同进制的100分别表示十进制数的多少呢?
十进制:100D = 1×102 + 0×101 + 0×100 = 100D
实战演练:
十进制换算为其他进制
除K取余法
举个例子:将(123)10 转换为二进制数
除K取余法:除2取余,商为0止,倒着排列
123
61
…………1
…………1
30
2
…………0
15
2
…………1
7
2
…………1
3
2
………..1
1
2
0
….…...1
2
2
( 123 )10
= ( 1111011 )2
亮 灭 灭 亮 灭
1 0 0 1 0
提示:烽火要么点燃要么不点燃,刚好是两种状态。
古代有一种传递信息的方式,是用点燃烽火的方式示警。假设规定点燃一个烽火台表示将有一万敌军来犯,问:
如果有18万敌军来犯,但仅有5个烽火台,要如何点燃烽火,传递正确信息呢?
余数
2
2
2
2
9
4
2
1
0
0
1
0
0
1
高位
2
18
低位
将18换算为二进制求得正确答案,点燃第一个和第四个烽火台。
最快解法:18=16+2=24+21
实战演练
拓展延伸
同样的假设:规定点燃一个烽火台表示将有一万敌军来犯。
①如果题目只告诉你有16万敌军来犯,问至少需要多少个烽火台才能通知正确消息,要怎么算?
16=24
1
0
0
0
0
至少5个烽火台
至少4个烽火台?
1
1
1
1
= (15)10
+1
拓展延伸
同样的假设:规定点燃一个烽火台表示将有一万敌军来犯。
②如果题目只告诉你有6个烽火台,问最多能够传达多少万敌军来犯的消息,要怎么算?
1位:可以表示2种状态,范围为0~1。
2位:可以表示4种状态,范围为0~3。
3位:可以表示8种状态,范围为0~7。
4位:可以表示16种状态,范围为0~15。
答:最多能够传达 26 - 1 = 63万
规律:n位二进制数,能表示 2n 种状态,所能表示的十进制数的范围是 0 ~ 2n -1
二进制与十六进制的换算
4个二进制数表示1个十六进制数
二进制数(1111)2: 1 1 1 1
位权:
1×23 +1×22 +1×21 +1×20
2n-1
=(15)10
十六进制数 (F)16: F
位权:
15×160
16n-1
=(15)10
原理讲解:
二进制与十六进制的换算
将(25)16 转换为二进制数
十六进制数(25)16 : 2 5
逐一换算为二进制:
( 00100101 )2
0101
0010
(25)16 =
实战演练:
4个二进制数表示1个十六进制数
二进制与十六进制的换算
将 (1001101001)2 转换为十六进制数
(1001101001)2 = (269)16
①从右开始,每四位数字成一组,不足四位数的往前补零;
即: 0010 0110 1001
②每四位数换算成一位十六进制数;
2、6、9
实战演练:
4个二进制数表示1个十六进制数
计算机中的数据是以二进制数字的形式进行加工、存储的。
计算机中数据的存储
计算机中存储数据的最小单位是二进制位,用比特(bit)表示。
计算机存储数据的基本单位是字节(Byte,简写为B),
1字节=8比特,即8位二进制数。
字节单位太小,常用的存储单位有KB、MB、GB等;更高的还有TB太字节、PB拍字节、EB艾字节。
1B能表示28(256)种状态
1B = 8b
存储单位 换算关系
B(byte),字节 1B = 8b(bit,位)
KB(kilobyte),千字节 1KB = 210B = 1024B
MB(megabyte),兆字节 1MB = 210KB = 1024KB
GB(gigabyte),吉字节 1GB =210MB = 1024MB
常见的数据存储单位
大B字节
小b比特
PART 01
PART 02
完成课本P20的习题
完成练习
预习编码的基本方式
预习新课
课后作业
下节再见
数据编码
高中信息技术必修一 数据与信息
第一课时
课前回顾
数据:现实世界客观事物的符号记录。
(文字、图形、图像、音频、视频等。)
什么是数据?
身份证
什么是编码?
将现实世界的事物现象符号化、数据化,称为编码。
什么是数据编码?
计算机将现实世界中的数据转换为“计算机中的数据”,这个过程就叫数据编码。
计算机中的数据是以二进制数字的形式进行加工、存储的。即文字、图片、音频、视频等信息在计算机中都是以二进制数形式存在的,表示信息类型不同,编码方案也不同。
晶体管只有两种状态
通电和断电,分别用 1 和 0 来表示
计算机中的数据
二进制数字是什么?和我们平时用的数字有什么不同?常见的数制有哪些呢?
进制与转换
02
生活中的进制
最常用的数制:十进制 —— 我们平时计算用的一般都是十进制,单个数位上最大数值为9,逢十进一。
1小时=60分钟,1分钟=60秒,用的是“六十进一”的计算方法。
1天=24小时,用的是“二十四进一”的计算方法。
“半斤八两”:古代1斤=16两,所以半斤和八两是一样多的,这里用的是十六进制。
数制
数制的基本要素:
数码:每位上可能的基本数字。
基数:每位上可能的数码个数。(划分数制)
位权:每位上“1”所表示的数值大小。
数制 数码 基数 基本计数规则 位权 表示方式
二进制 B(binary) 0,1 2 逢二进一 2n-1 (1001)2
1001B
八进制 O(octal) 0,1,2,3,4,5,6,7 8 逢八进一 8n-1 (1001)8
1001O
十进制 D(decimal) 0,1,2,3,4,5,6,7,8,9 10 逢十进一 10n-1 (1001)10
1001D
十六进制 H(hexadecimal) 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 16 逢十六进一 16n-1 (1001)16
1001H
数字换算为十进制
数权相乘再相加
十进制数123: 1 2 3
位权:
1×102 + 2×101 + 3×100
102
100
101
10n-1
(123)10 =
原理讲解:
数字换算为十进制
数权相乘再相加
二进制数1101: 1 1 0 1
位权:
1×23 +1×22 +0×21 +1×20
22
20
21
23
2n-1
(13)10 =
实战演练:
进制转换练习
二进制:100B =
十六进制:100H =
1×22 + 0×21 + 0×20
= 4D
八进制:100O =
1×82 + 0×81 + 0×80
= 64D
1×162 + 0×161 + 0×160 = 256D
练习:不同进制的100分别表示十进制数的多少呢?
十进制:100D = 1×102 + 0×101 + 0×100 = 100D
实战演练:
十进制换算为其他进制
除K取余法
举个例子:将(123)10 转换为二进制数
除K取余法:除2取余,商为0止,倒着排列
123
61
…………1
…………1
30
2
…………0
15
2
…………1
7
2
…………1
3
2
………..1
1
2
0
….…...1
2
2
( 123 )10
= ( 1111011 )2
亮 灭 灭 亮 灭
1 0 0 1 0
提示:烽火要么点燃要么不点燃,刚好是两种状态。
古代有一种传递信息的方式,是用点燃烽火的方式示警。假设规定点燃一个烽火台表示将有一万敌军来犯,问:
如果有18万敌军来犯,但仅有5个烽火台,要如何点燃烽火,传递正确信息呢?
余数
2
2
2
2
9
4
2
1
0
0
1
0
0
1
高位
2
18
低位
将18换算为二进制求得正确答案,点燃第一个和第四个烽火台。
最快解法:18=16+2=24+21
实战演练
拓展延伸
同样的假设:规定点燃一个烽火台表示将有一万敌军来犯。
①如果题目只告诉你有16万敌军来犯,问至少需要多少个烽火台才能通知正确消息,要怎么算?
16=24
1
0
0
0
0
至少5个烽火台
至少4个烽火台?
1
1
1
1
= (15)10
+1
拓展延伸
同样的假设:规定点燃一个烽火台表示将有一万敌军来犯。
②如果题目只告诉你有6个烽火台,问最多能够传达多少万敌军来犯的消息,要怎么算?
1位:可以表示2种状态,范围为0~1。
2位:可以表示4种状态,范围为0~3。
3位:可以表示8种状态,范围为0~7。
4位:可以表示16种状态,范围为0~15。
答:最多能够传达 26 - 1 = 63万
规律:n位二进制数,能表示 2n 种状态,所能表示的十进制数的范围是 0 ~ 2n -1
二进制与十六进制的换算
4个二进制数表示1个十六进制数
二进制数(1111)2: 1 1 1 1
位权:
1×23 +1×22 +1×21 +1×20
2n-1
=(15)10
十六进制数 (F)16: F
位权:
15×160
16n-1
=(15)10
原理讲解:
二进制与十六进制的换算
将(25)16 转换为二进制数
十六进制数(25)16 : 2 5
逐一换算为二进制:
( 00100101 )2
0101
0010
(25)16 =
实战演练:
4个二进制数表示1个十六进制数
二进制与十六进制的换算
将 (1001101001)2 转换为十六进制数
(1001101001)2 = (269)16
①从右开始,每四位数字成一组,不足四位数的往前补零;
即: 0010 0110 1001
②每四位数换算成一位十六进制数;
2、6、9
实战演练:
4个二进制数表示1个十六进制数
计算机中的数据是以二进制数字的形式进行加工、存储的。
计算机中数据的存储
计算机中存储数据的最小单位是二进制位,用比特(bit)表示。
计算机存储数据的基本单位是字节(Byte,简写为B),
1字节=8比特,即8位二进制数。
字节单位太小,常用的存储单位有KB、MB、GB等;更高的还有TB太字节、PB拍字节、EB艾字节。
1B能表示28(256)种状态
1B = 8b
存储单位 换算关系
B(byte),字节 1B = 8b(bit,位)
KB(kilobyte),千字节 1KB = 210B = 1024B
MB(megabyte),兆字节 1MB = 210KB = 1024KB
GB(gigabyte),吉字节 1GB =210MB = 1024MB
常见的数据存储单位
大B字节
小b比特
PART 01
PART 02
完成课本P20的习题
完成练习
预习编码的基本方式
预习新课
课后作业
下节再见
