直线与圆、圆与圆的位置关系(浙江省杭州市萧山市)
文档属性
| 名称 | 直线与圆、圆与圆的位置关系(浙江省杭州市萧山市) |

|
|
| 格式 | rar | ||
| 文件大小 | 297.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-02 00:00:00 | ||
图片预览



文档简介
课件24张PPT。直线与圆的位置关系(复习课)2007中考考试目标38.圆的切线
(1)了解切线的概念 b
(2)探索切线与过切点的半径之间的关系 a
(3)能判定一条直线是否为圆的切线 c
⑷会过圆上一点画圆的切线 c
⑸了解圆周角与圆心角的关系、直径所对圆周角的特征 a
⑹了解三角形内心和外心 a37.圆的基本性质
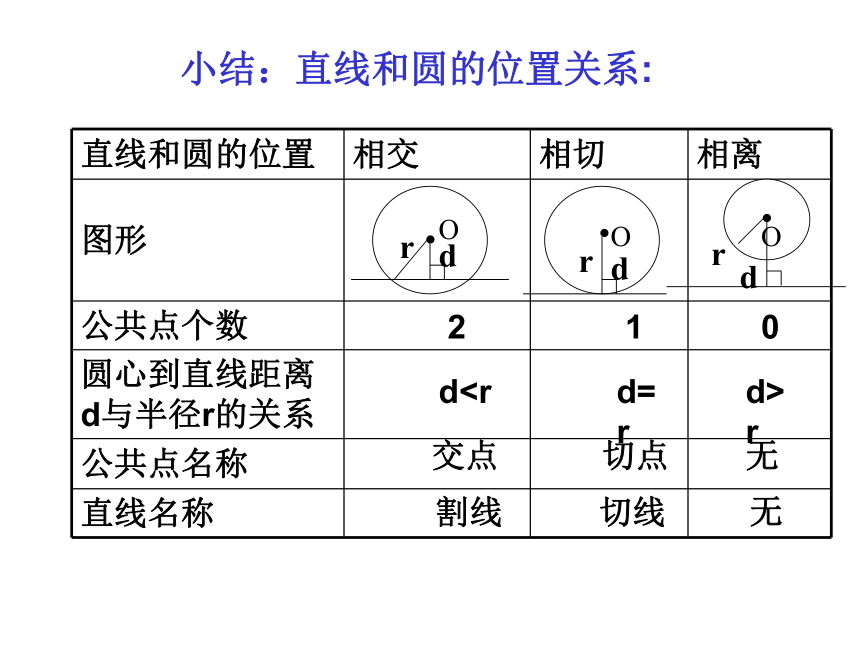
(1)探索并了解直线与圆以及圆与圆的位置关系c 小结:直线和圆的位置关系:210dr交点切点无 割线 切线 无O?drOl?drO ?dr切线的判定定理:
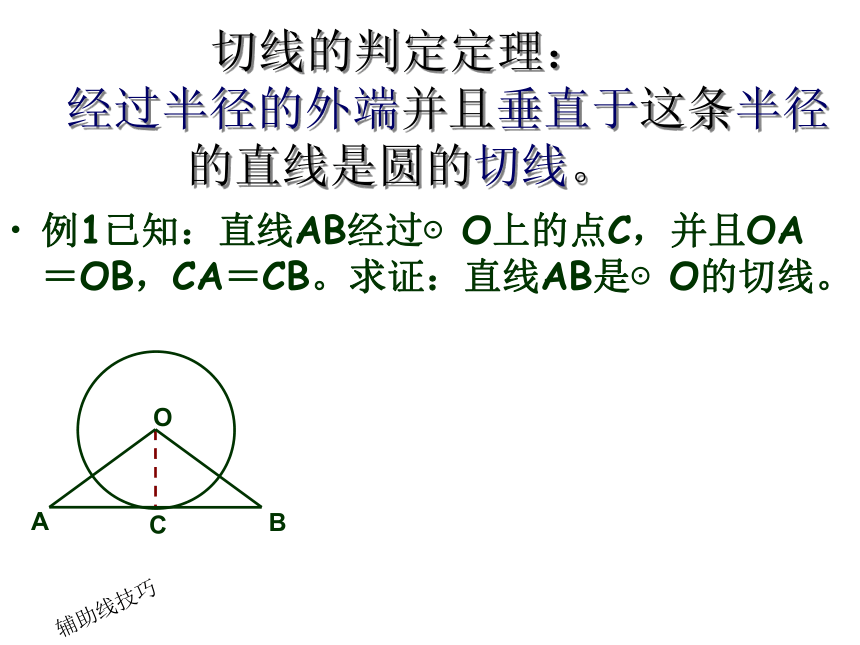
经过半径的外端并且垂直于这条半径的直线是圆的切线。例1已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。辅助线技巧
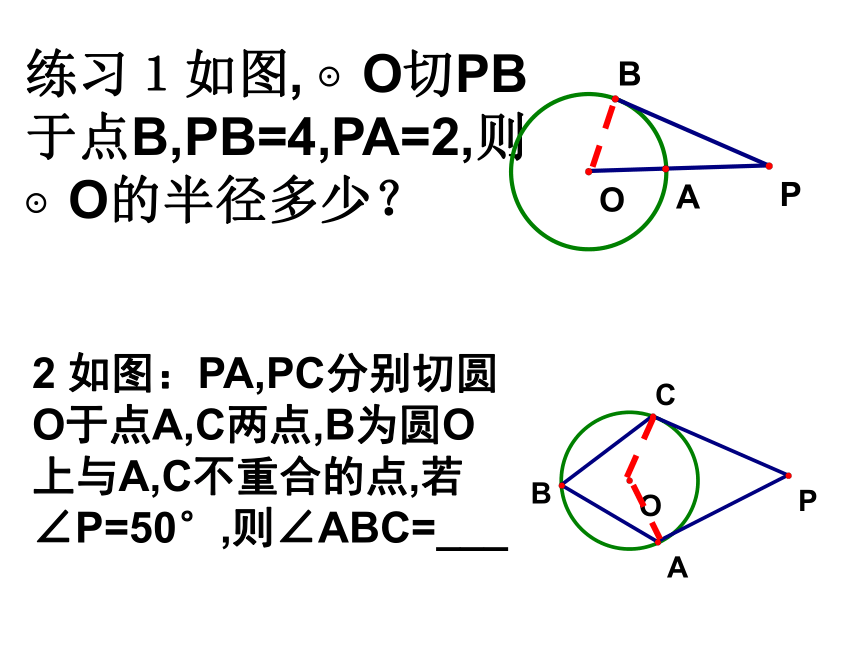
练习1如图, ⊙O切PB于点B,PB=4,PA=2,则
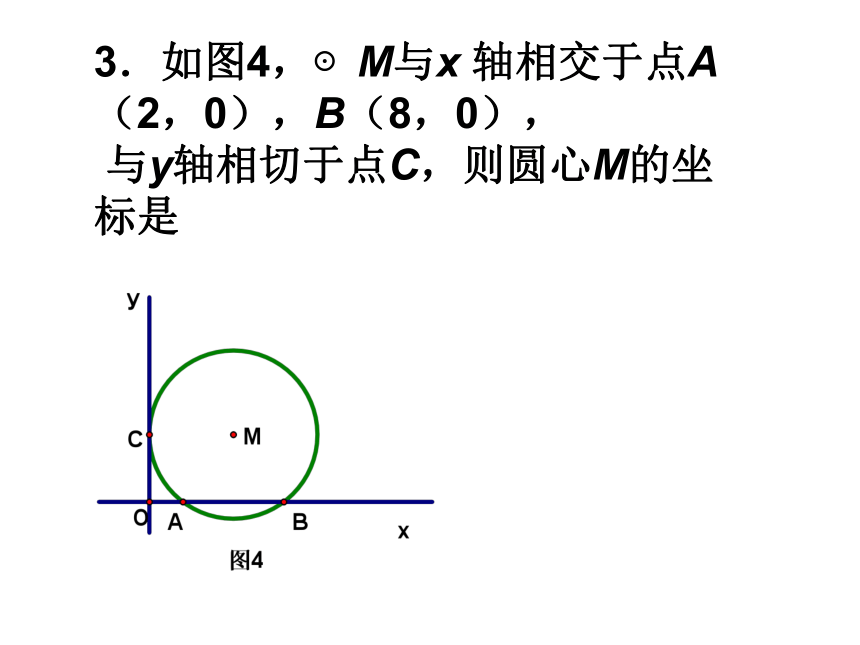
⊙O的半径多少?2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___3.如图4,⊙M与x 轴相交于点A(2,0),B(8,0),
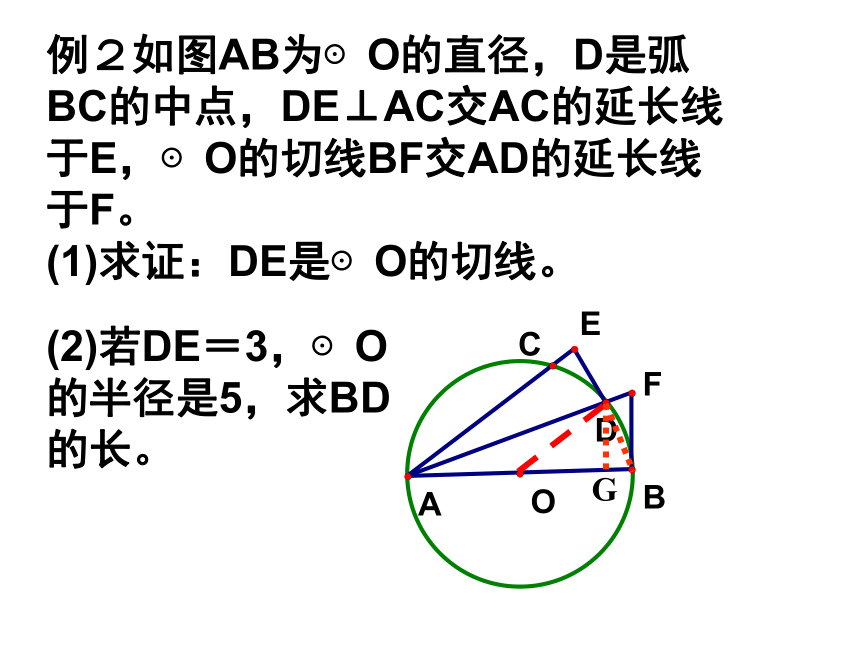
与y轴相切于点C,则圆心M的坐标是 例2如图AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F。
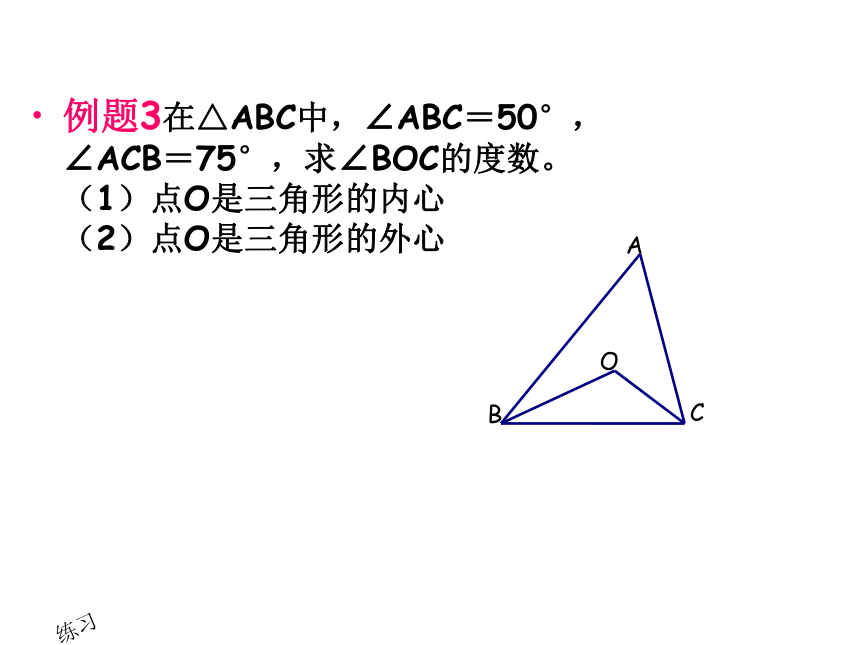
(1)求证:DE是⊙O的切线。 (2)若DE=3,⊙O的半径是5,求BD的长。 G例题3在△ABC中,∠ABC=50°,∠ACB=75°,求∠BOC的度数。 (1)点O是三角形的内心 (2)点O是三角形的外心练习三条高线的交点三条角平分线的交点三边垂直平分线的交点三条中线的交点在三角形内、形外或直角顶点在三角形内、形外或斜边中点在三角形形内在三角形形内到三角形各顶点距离相等到三角形三边距离相等把中线分成了2:1两部分特殊三角形外接圆、内切圆半径的求法:直角三角形外接圆、内切圆半径的求法等边三角形外接圆、 内切圆半径的求法基本思路:
构造三角形BOD,BO为外接圆半径,DO为内切圆半径。OD直角三角形的内切圆练习1.已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,∠AC=3,BC=4.
求⊙O的半径r. 驶向胜利的彼岸老师提示:
作过切点的半径,应用题一的结论.6.已知△ABC,AC=12,BC=5,AB=13。则△ABC的外接圆半径为 。
7. 正三角形的边长为a,它的内切圆和外接圆的半径分别是______ , ____
直角三角形的内切圆练习2.已知:如图,△ABC的面积S=4cm2,周长等于10cm.
求内切圆⊙O的半径r.驶向胜利的彼岸老师提示:
△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积.如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.2变式1:CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△ PCD的周长为____.4综合运用变式2:改变切点E的位置(在劣弧AB上),则△ PCD的周长为____.变式3:若PA=5则△ PCD的周长为____.
410变式4:若PA=a,则△ PCD的周长为____.
2a
如图,圆o内切于△ABC,切点分别为D、E、F。 已知∠C=600,∠B=500,连接OE、OF、DE、DF,那么∠EDF等于
A B
C D如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 。1、如图,点P在圆O的直径BA的延长线上,
AB=2PA,PC切圆O于点C,连接BC
(1)求的正弦值;
(2)若圆O的半径r=2cm,求BC的长度圆与圆的位置关系复习知识要点1.圆与圆的位置关系有 种,分别是 , ,
, , .内含内切相交外切外离5切点d=R+rd=R-r知识要点d>R+rR-r<d< R+rd<R-r感悟、渗透、应用【例1】如图所示,已知AB为⊙O的直径,C为AB延长线上的点,以OC为直径的圆交⊙O于D,连结AD,BD,CD.
(1)求证:CD是⊙O的切线;
(2)若AB=BC=2,求tan ∠A的值.【解析】
(1)证∠CDO=90°即可,理由OC为圆的直径.
(2)利用△BCD∽△DCA得到BD8DA的比值1.两圆内切,其中一个圆的半径为5,两圆的圆心距为2,
则另一个圆的半径是 . 2. 已知两圆的圆心距是3,两圆的半径分别1,3,则这两个
圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切3.已知⊙O1与⊙O2内切,它们的半径分别为2和3,
则这两圆的圆心距d满足( )
(A)d=5 (B)d=1 (C)1<d<5 (D)d >54.已知半径均为1厘米的两圆外切,半径为2厘米,且和这两圆都相切的圆共有( )
(A)2个 (B)3个 (C)4个 (D)5个5、如图,施工工地的水平地面上有三根直径
都是1米的水泥管,两两相切地堆放在一
起,则其最高点到地面的距离是 . 例10(05湖北黄冈实验区)如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA = EC。
⑴ 求证:AC 2 = AE·AB;
⑵ 延长EC到点P,连结PB,若PB = PE,试判断PB与⊙O的位置关系,并说明理由。
(1)了解切线的概念 b
(2)探索切线与过切点的半径之间的关系 a
(3)能判定一条直线是否为圆的切线 c
⑷会过圆上一点画圆的切线 c
⑸了解圆周角与圆心角的关系、直径所对圆周角的特征 a
⑹了解三角形内心和外心 a37.圆的基本性质
(1)探索并了解直线与圆以及圆与圆的位置关系c 小结:直线和圆的位置关系:210d
练习1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___3.如图4,⊙M与x 轴相交于点A(2,0),B(8,0),
与y轴相切于点C,则圆心M的坐标是 例2如图AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F。
(1)求证:DE是⊙O的切线。 (2)若DE=3,⊙O的半径是5,求BD的长。 G例题3在△ABC中,∠ABC=50°,∠ACB=75°,求∠BOC的度数。 (1)点O是三角形的内心 (2)点O是三角形的外心练习三条高线的交点三条角平分线的交点三边垂直平分线的交点三条中线的交点在三角形内、形外或直角顶点在三角形内、形外或斜边中点在三角形形内在三角形形内到三角形各顶点距离相等到三角形三边距离相等把中线分成了2:1两部分特殊三角形外接圆、内切圆半径的求法:直角三角形外接圆、内切圆半径的求法等边三角形外接圆、 内切圆半径的求法基本思路:
构造三角形BOD,BO为外接圆半径,DO为内切圆半径。OD直角三角形的内切圆练习1.已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,∠AC=3,BC=4.
求⊙O的半径r. 驶向胜利的彼岸老师提示:
作过切点的半径,应用题一的结论.6.已知△ABC,AC=12,BC=5,AB=13。则△ABC的外接圆半径为 。
7. 正三角形的边长为a,它的内切圆和外接圆的半径分别是______ , ____
直角三角形的内切圆练习2.已知:如图,△ABC的面积S=4cm2,周长等于10cm.
求内切圆⊙O的半径r.驶向胜利的彼岸老师提示:
△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积.如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.2变式1:CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△ PCD的周长为____.4综合运用变式2:改变切点E的位置(在劣弧AB上),则△ PCD的周长为____.变式3:若PA=5则△ PCD的周长为____.
410变式4:若PA=a,则△ PCD的周长为____.
2a
如图,圆o内切于△ABC,切点分别为D、E、F。 已知∠C=600,∠B=500,连接OE、OF、DE、DF,那么∠EDF等于
A B
C D如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 。1、如图,点P在圆O的直径BA的延长线上,
AB=2PA,PC切圆O于点C,连接BC
(1)求的正弦值;
(2)若圆O的半径r=2cm,求BC的长度圆与圆的位置关系复习知识要点1.圆与圆的位置关系有 种,分别是 , ,
, , .内含内切相交外切外离5切点d=R+rd=R-r知识要点d>R+rR-r<d< R+rd<R-r感悟、渗透、应用【例1】如图所示,已知AB为⊙O的直径,C为AB延长线上的点,以OC为直径的圆交⊙O于D,连结AD,BD,CD.
(1)求证:CD是⊙O的切线;
(2)若AB=BC=2,求tan ∠A的值.【解析】
(1)证∠CDO=90°即可,理由OC为圆的直径.
(2)利用△BCD∽△DCA得到BD8DA的比值1.两圆内切,其中一个圆的半径为5,两圆的圆心距为2,
则另一个圆的半径是 . 2. 已知两圆的圆心距是3,两圆的半径分别1,3,则这两个
圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切3.已知⊙O1与⊙O2内切,它们的半径分别为2和3,
则这两圆的圆心距d满足( )
(A)d=5 (B)d=1 (C)1<d<5 (D)d >54.已知半径均为1厘米的两圆外切,半径为2厘米,且和这两圆都相切的圆共有( )
(A)2个 (B)3个 (C)4个 (D)5个5、如图,施工工地的水平地面上有三根直径
都是1米的水泥管,两两相切地堆放在一
起,则其最高点到地面的距离是 . 例10(05湖北黄冈实验区)如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA = EC。
⑴ 求证:AC 2 = AE·AB;
⑵ 延长EC到点P,连结PB,若PB = PE,试判断PB与⊙O的位置关系,并说明理由。
