【同步分层作业】3.4圆心角(含解析)
文档属性
| 名称 | 【同步分层作业】3.4圆心角(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 812.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-12 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.4圆心角 同步分层作业
基础过关
1.如图,AB是⊙O的直径,==,若∠COD=35°,则∠AOE的度数是( )
A.35° B.55° C.75° D.95°
2.如图,点A,B,C,D是⊙O上的四个点,且AB=CD,OE⊥AB,OF⊥CD,则下列结论错误的是( )
A. B.OE=OF C.∠AOB=∠COD D.
3.在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.120° B.75° C.60° D.30°
4.已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆心角的度数为( )
A.45° B.90° C.90° 或270° D.45°或135°
5.如图,AB,CD是⊙O的直径,,若∠AOE=32°,则∠COE的度数是 .
6.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
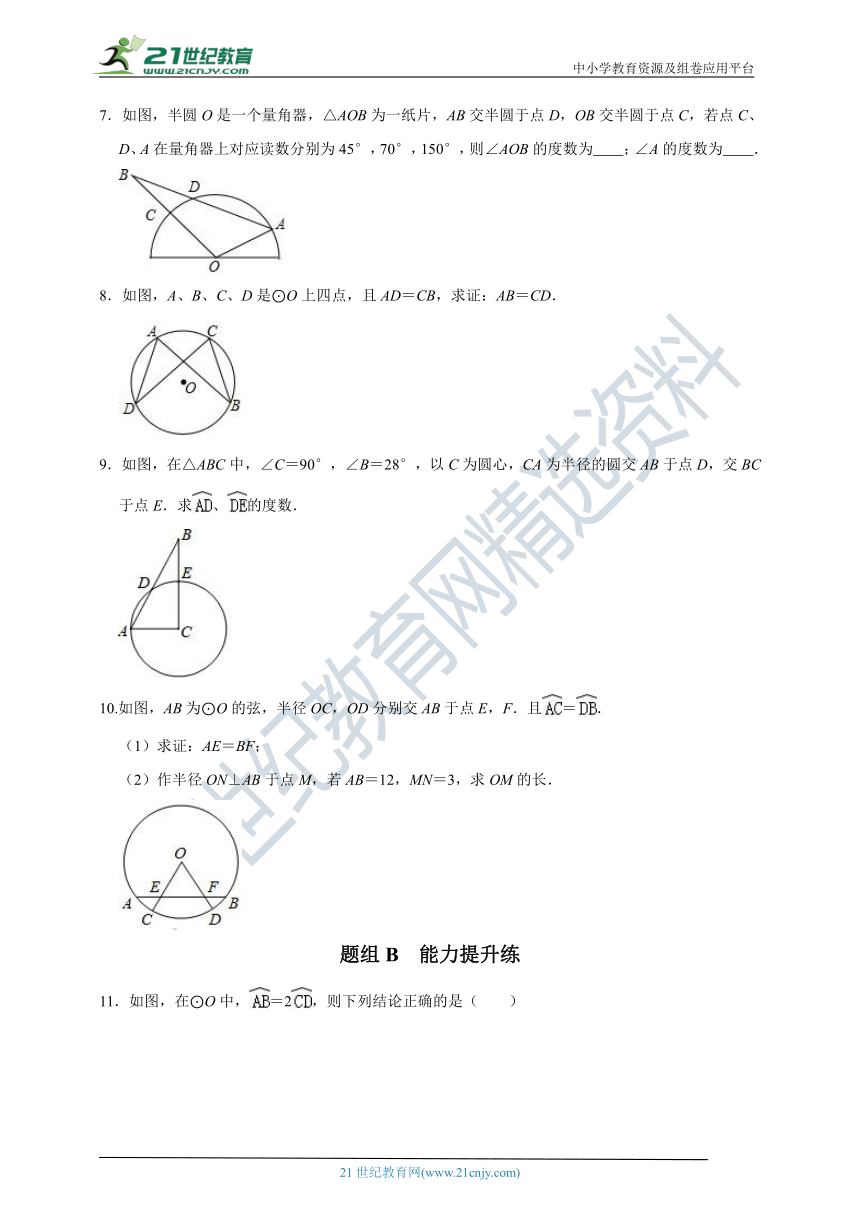
7.如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为 ;∠A的度数为 .
8.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
9.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求、的度数.
10.如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F.且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
题组B 能力提升练
11.如图,在⊙O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD C.AB<2CD D.以上都不正确
12.如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F.若,AE=2,则⊙O的直径长为( )
A. B.8 C.10 D.
13.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
14.如图,在半径为10的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
A.6 B. C.8 D.
15.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°,AE交⊙O于点B,且AB=OD.则∠EOD= .
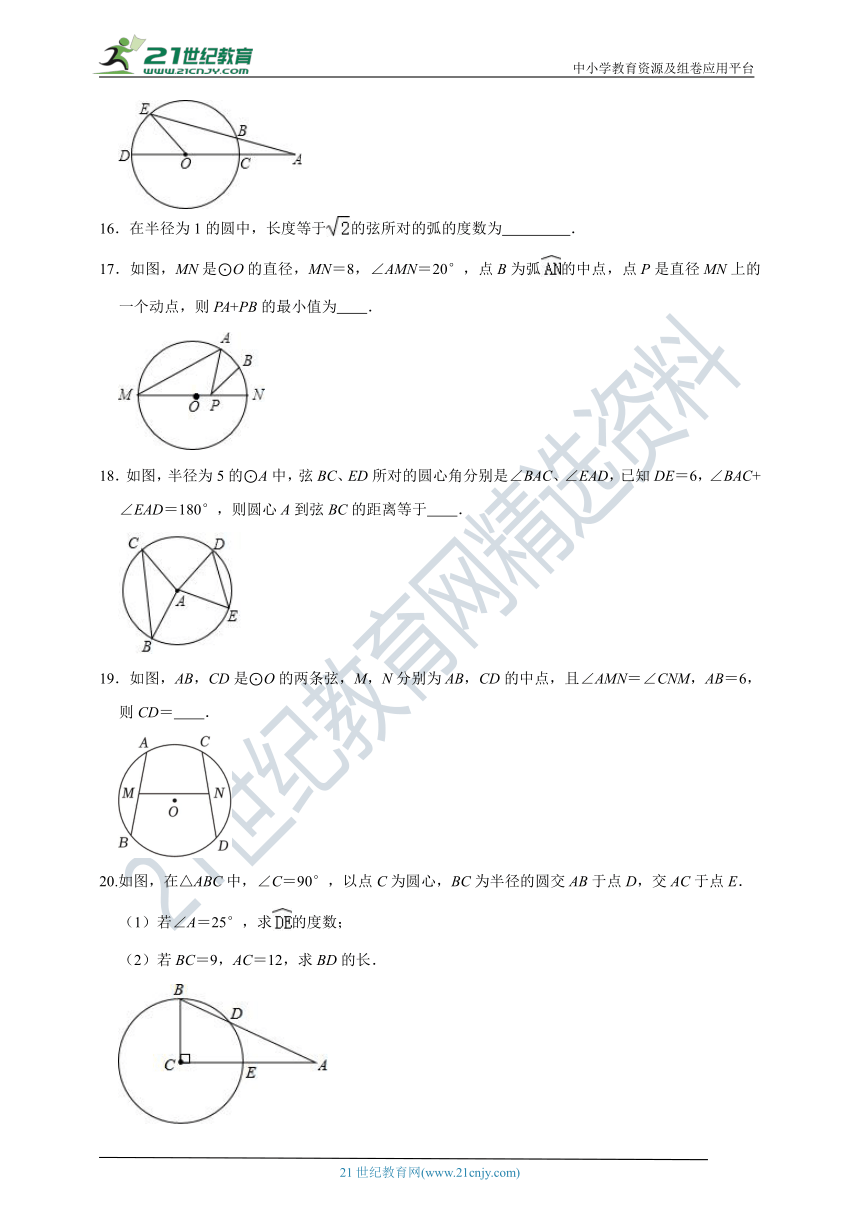
16.在半径为1的圆中,长度等于的弦所对的弧的度数为 .
17.如图,MN是⊙O的直径,MN=8,∠AMN=20°,点B为弧的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 .
18.如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于 .
19.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= .
20.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
21.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
22.如图,已知圆O的弦AB与直径CD交于点E,且CD平分AB.
(1)已知AB=6,EC=2,求圆O的半径;
(2)如果DE=3EC,求弦AB所对的圆心角的度数.
题组C 培优拔尖练
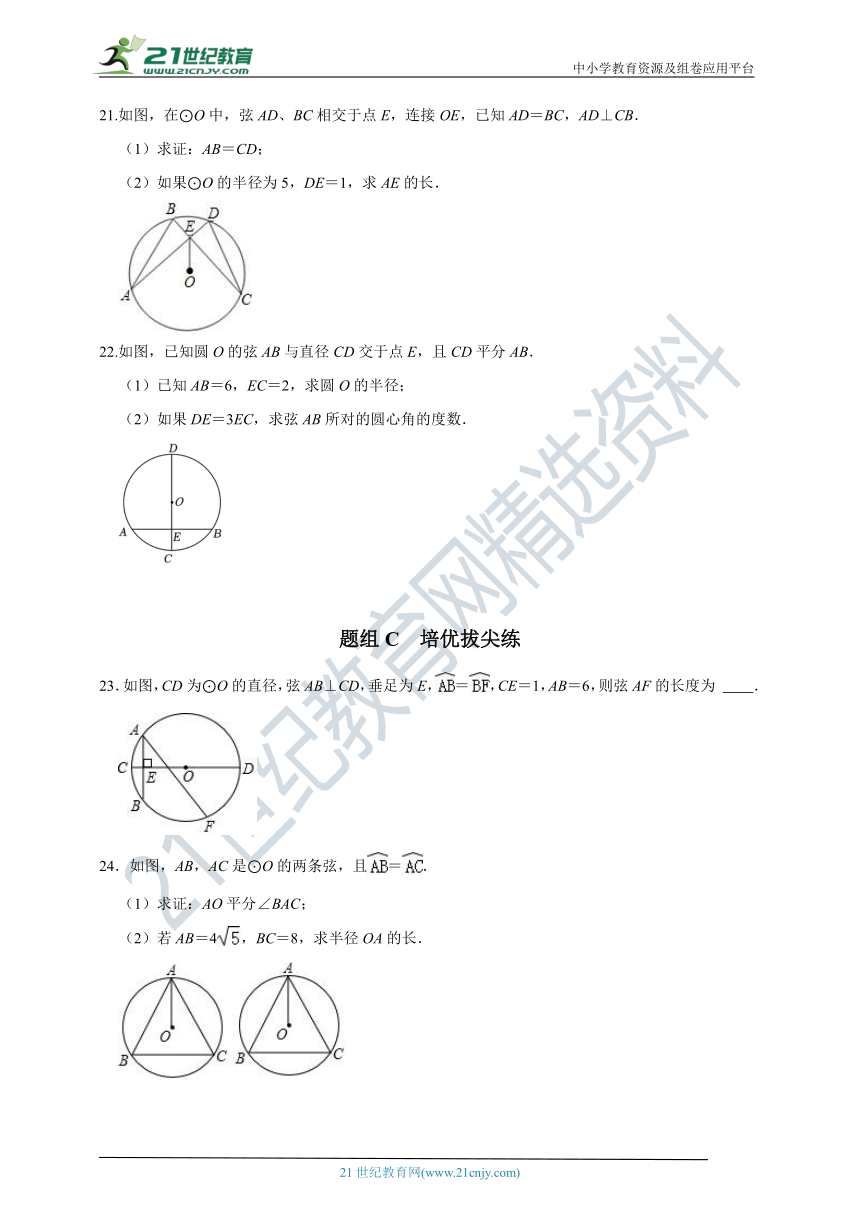
23.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
24.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
答案与解析
基础过关
1.如图,AB是⊙O的直径,==,若∠COD=35°,则∠AOE的度数是( )
A.35° B.55° C.75° D.95°
【点拨】由,可求得∠BOC=∠EOD=∠COD=35°,继而可求得∠AOE的度数.
【解析】解:∵,
∴∠BOC=∠EOD=∠COD=35°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=75°.
故选:C.
【点睛】此题考查了弧与圆心角的关系,掌握数形结合思想的应用是解题的关键.
2.如图,点A,B,C,D是⊙O上的四个点,且AB=CD,OE⊥AB,OF⊥CD,则下列结论错误的是( )
A. B.OE=OF C.∠AOB=∠COD D.
【点拨】根据圆心角、弧、弦的关系即可判断出答案.
【解析】解:A、∵AB=CD,∴=,故不符合题意;
B、∵OE⊥AB,OF⊥CD,
∴AE=AB,DF=CD,
∵AB=CD,
∴AE=DF,
∵OA=OD,
∴Rt△AOE≌Rt△DOF,
∴OE=OF,故不符合题意;
C、∵AB=CD,∴∠AOB=∠COD,故不符合题意;
D、根据已知条件得不到=,故符合题意.
故选:D.
【点睛】本题主要考查圆心角、弧、弦的关系和垂径定理,解题的关键是掌握在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.
3.在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.120° B.75° C.60° D.30°
【点拨】连接OA、OB,如图,通过证明△OAB为等边三角形得到∠AOB=60°.
【解析】解:连接OA、OB,如图,
∵OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
即弦AB所对应的圆心角的度数为60°.
故选:C.
【点睛】本题考查了圆心角、弧、弦的关系,利用半径相等构建等腰三角形是解决问题的关键.
4.已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆心角的度数为( )
A.45° B.90° C.90° 或270° D.45°或135°
【点拨】根据弦AB把圆周分成1:3的两部分求出的度数,再根据圆心角的度数等于它所对的弧的度数求出答案即可.
【解析】解:∵弦AB把圆周分成1:3的两部分,
∴的度数是×360°=90°,
∴圆心角∠AOB的度数是90°或360°﹣90°=270°,
故选:C.
【点睛】本题考查了圆心角、弧、弦之间的关系,能求出的度数是解此题的关键.
5.如图,AB,CD是⊙O的直径,,若∠AOE=32°,则∠COE的度数是 64° .
【点拨】根据在同圆中,等弧所对的圆心角相等,可推出∠BOD=∠AOE=32°,再根据对顶角相等,可推出∠AOC=∠BOD=32°,最后用∠COE=∠COA+∠AOE即可求解.
【解析】解:∵,∠AOE=32°,
∴∠BOD=∠AOE=32°,
∵∠AOC=∠BOD=32°,
∴∠COE=∠COA+∠AOE=32°+32°=64°.
故答案为:64°.
【点睛】本题主要考查等弧和圆心角的关系,熟知在同圆中,等弧所对的圆心角相等,和对顶角相等是解题的关键.
6.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 105° .
【点拨】连接OD,OE,根据圆心角、弧、弦的关系定理求出∠AOD=35°,根据等腰三角形的性质和三角形内角和定理计算即可.
【解析】解:如图,连接OD,OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=110°,
∴∠AOE=75°,
∴∠BOE=105°,
∴的度数是105°.
故答案为105°.
【点睛】本题考查的是圆心角、弧、弦的关系定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
7.如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为 105° ;∠A的度数为 50° .
【点拨】根据量角器的知识,可直接求出∠AOB,连接OD,求出∠AOD,利用等腰三角形的性质可得∠A的度数.
【解析】解:
∵点C、D、A在量角器上对应读数分别为45°,70°,150°,
∴∠AOB=∠MOA﹣∠MOC=150°﹣45°=105°,
连接OD,则OA=OD,
∵∠AOD=150°﹣70°=80°,
∴∠A=(180°﹣80°)=50°.
故答案为:105°,50°.
【点睛】本题考查了圆周角定理的知识,解答本题的关键是掌握量角器的应用.
8.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
【点拨】根据圆心角、弧、弦之间的关系得出即可.
【解析】证明:∵AD=CB,
∴=,
∴+=+,
即=,
∴AB=CD.
【点睛】本题考查了圆心角、弧、弦之间的关系,能根据定理求出=是解此题的关键.
9.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求、的度数.
【点拨】连接CD,如图,利用互余计算出∠A=62°,则∠A=∠ADC=62°,再根据三角形内角和定理计算出∠ACD=56°,接着利用互余计算出∠DCE=34°,然后根据圆心角的度数等于它所对弧的度数求解.
【解析】解:连接CD,如图,
∵∠C=90°,∠B=28°,
∴∠A=90°﹣28°=62°,
∵CA=CD,
∴∠A=∠ADC=62°,
∴∠ACD=180°﹣2×62°=56°
∴的度数为56°;
∵∠DCE=90°﹣∠ACD=34°,
∴的度数为34°.
【点睛】本题考查的是圆心角、弧、弦的关系、等腰三角形的性质,掌握圆心角、弧、弦的关系定理是解题的关键.
10.如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F.且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
【点拨】(1)连接OA、OB,证明△AOE≌△BOF(ASA),即可得出结论;
(2)连接OA,由垂径定理得出AM=AB=6,设OM=x,则OA=ON=x+3,在Rt△AOM中,由勾股定理得出方程,解方程即可.
【解析】(1)证明:连接OA、OB,如图1所示:
∵OA=OB,
∴∠A=∠B,
∵=,
∴∠AOE=∠BOF,
在△AOE和△OBF中,
,
∴△AOE≌△BOF(ASA),
∴AE=BF.
(2)解:连接OA,如图2所示:
∵OM⊥AB,
∴AM=AB=6,
设OM=x,则OA=ON=x+3,
在Rt△AOM中,由勾股定理得:62+x2=(x+3)2,
解得:x=4.5,
∴OM=4.5.
【点睛】本题考查垂径定理,勾股定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
题组B 能力提升练
11.如图,在⊙O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD C.AB<2CD D.以上都不正确
【点拨】首先取的中点E,连接AE,BE,由在⊙O中,=2,可证得==,即可得AE=BE=CD,然后由三角形的三边关系,求得答案.
【解析】解:取的中点E,连接AE,BE,
∵在⊙O中,=2,
∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴2CD>AB.
故选:C.
【点睛】此题考查了弧与弦的关系以及三角形的三边关系.注意在同圆或等圆中,同弧或等弧,所对的弦相等.
12.如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F.若,AE=2,则⊙O的直径长为( )
A. B.8 C.10 D.
【点拨】连接OF,首先证明,设OA=OF=x,在Rt△OEF中,利用勾股定理构建方程即可解决问题.
【解析】解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,,
∵点D是弧AC的中点,
∴,
∴,
∴,
∴,
设OA=OF=x,
在Rt△OEF中,则有,
解得x=4,
∴AB=2x=8.
故选:B.
【点睛】本题考查勾股定理,垂径定理,弧,弦之间的关系等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
13.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
【点拨】过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,由于DE=FG=MN,所以弦的弦心距也相等,所以OB、OC是角平分线,可求出∠POQ,进而可求出∠BOC.
【解析】解:如图,过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,
∴∠APO=∠AQO=90°,
∵∠A=50°,
∴∠POQ=360°﹣90°﹣90°﹣50°=130°,
∵DE=FG=MN,
∴OP=OK=OQ,
∴OB、OC平分∠ABC和∠ACB,
∴∠BOC==115°.
故选:C.
【点睛】本题主要考查垂径定理,解题关键是构造出辅助线——弦心距.
14.如图,在半径为10的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
A.6 B. C.8 D.
【点拨】作OM⊥AB于M,ON⊥CD于N,连接OB,OD,首先利用勾股定理求得OM的长,然后判定四边形OMPN是正方形,求得正方形的对角线的长即可求得OM的长.
【解析】解:作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
由垂径定理、勾股定理得:OM=ON==6,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=6.
故选:B.
【点睛】本题考查了垂径定理及勾股定理的知识,解题的关键是正确地作出辅助线.
15.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°,AE交⊙O于点B,且AB=OD.则∠EOD= 54° .
【点拨】连接OB,根据等腰三角形的性质求出∠A=∠BOA=18°,根据三角形外角性质求出∠EBO,根据等腰三角形的性质求出∠E,再根据三角形的外角性质求出答案即可.
【解析】解:连接OB,
∵AB=OD,OD=OB,
∴AB=OB,
∴∠BOA=∠A,
∵∠A=18°,
∴∠BOA=18°,
∴∠EBO=∠A+∠BOA=36°,
∵OE=OB,
∴∠E=∠EBO=36°,
∵∠A=18°,
∴∠EOD=∠A+∠E=18°+36°=54°,
故答案为:54°.
【点睛】本题考查了等腰三角形的性质和三角形的外角性质,能熟记等腰三角形的性质和三角形的外角性质是解此题的关键,注意:等边对等角,三角形的一个外角等于与它不相邻的两个内角的和.
16.在半径为1的圆中,长度等于的弦所对的弧的度数为 90°或270° .
【点拨】如图,⊙O的半径为1,弦AB=,连接OA、OB,利用勾股定理的逆定理可判断△OAB为等腰直角三角形,则∠AOB=90°,然后根据圆心角的度数等于它所对的弧的度数求解.
【解析】解:如图,⊙O的半径为1,弦AB=,
连接OA、OB,
∵OA=OB=1,
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,
∴∠AOB=90°,
∴AB所所的弧的度数为90°或270°.
故答案为90°或270°.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
17.如图,MN是⊙O的直径,MN=8,∠AMN=20°,点B为弧的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 4 .
【点拨】过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,由对称的性质可知=,再由圆周角定理可求出∠A′ON的度数,再由勾股定理即可求解.
【解析】解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,
连接OB,OA′,AA′,
∵AA′关于直线MN对称,
∴=,
∵∠AMN=20°,
∴∠A′ON=40°,∠BON=20°,
∴∠A′OB=60°,
∴△A′OB是等边三角形,
∴A′B=MN=4,即PA+PB的最小值4.
故答案为:4.
【点睛】本题考查的是圆心角、弧、弦的关系及轴对称﹣最短路线问题,解答此题的关键是根据题意作出辅助线,构造出直角三角形,利用勾股定理求解.
18.如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于 3 .
【点拨】作AH⊥BC于H,作直径CF,连接BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=BF=3.
【解析】解:作AH⊥BC于H,作直径CF,连接BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵CA=AF,
∴AH为△CBF的中位线,
∴AH=BF=3.
∴点A到弦BC的距离为:3.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
故答案为:3.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和三角形中位线性质.
19.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= 6 .
【点拨】连接OM,ON,OA,OC,先根据垂径定理得出AM=AB,CN=CD,再由∠AMN=∠CNM得出∠NMO=∠MNO,即OM=ON,再由OA=OC可知Rt△AOM≌Rt△CON,故AM=CN,由此即可得出结论.
【解析】解:连接OM,ON,OA,OC,
∵M、N分别为AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴AM=AB,CN=CD,
∵∠AMN=∠CNM,
∴∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
,
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
∴AB=CD=6.
故答案为:6.
【点睛】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
20.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
【点拨】(1)求出∠B的度数,求出∠B所对的弧的度数,即可得出答案;
(2)根据勾股定理求出AB,根据割线定理得出比例式,即可得出答案.
【解析】解:(1)连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴∠DCE=40°,
∴的度数为40°;
(2)延长AC交⊙C与点F,
∵∠BCA=90°,CF=BC=9,AC=12,
∴AB=,AE=12﹣9=3.AF=AC+CF=12+9=21,
∵AB与AF均是⊙C的割线,
∴AD AB=AE AF,即15AD=3×21,解得AD=,
∴BD=AB﹣AD=15﹣=.
【点睛】本题考查了勾股定理,割线定理圆心角、弧、弦之间的关系,切割线定理的应用,能综合运用知识点进行计算是解此题的关键.
21.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
【点拨】(1)欲证明AB=CD,只需证得=;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.构建正方形EFOG,利用正方形的性质,垂径定理和勾股定理来求AF的长度,则易求AE的长度.
【解析】(1)证明:如图,∵AD=BC,
∴=,
∴﹣=﹣,即=
∴AB=CD;
(2)解:如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.
【点睛】本题考查了勾股定理,正方形的判定与性质,垂径定理以及圆周角、弧、弦间的关系.注意(2)中辅助线的作法.
22.如图,已知圆O的弦AB与直径CD交于点E,且CD平分AB.
(1)已知AB=6,EC=2,求圆O的半径;
(2)如果DE=3EC,求弦AB所对的圆心角的度数.
【点拨】(1)连接OA,如图,设⊙O的半径为r,则OA=r,OE=r﹣2,先根据垂径定理得到AE=BE=3,CD⊥AB,在Rt△OAE中利用勾股定理得到32+(r﹣2)2=r2,然后解方程即可;
(2)连接OB,如图,先利用DE=3EC得到OE=CE,即OE=OA,再利用正弦的定义得到∠A=30°,然后根据等腰三角形的性质和三角形内角和定理计算∠AOB即可.
【解析】解:(1)连接OA,如图,设⊙O的半径为r,则OA=r,OE=r﹣2,
∵CD平分AB,
∴AE=BE=3,CD⊥AB,
在Rt△OAE中,32+(r﹣2)2=r2,
解得r=,
即⊙O的半径为;
(2)连接OB,如图,
∵DE=3EC,
∴OC+OE=3EC,
即OE+CE+OE=3CE,
∴OE=CE,
∴OE=OC=OA,
在Rt△OAE中,∵sinA==,
∴∠A=30°,
∵OA=OB,
∴∠B=∠A=30°,
∴∠AOB=180°﹣∠A﹣∠B=120°,
即弦AB所对的圆心角的度数为120°.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理和勾股定理.
题组C 培优拔尖练
23.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
【点拨】连接OA、OB,OB交AF于G,如图,利用垂径定理得到AE=BE=3,设⊙O的半径为r,则OE=r﹣1,OA=r,根据勾股定理得到32+(r﹣1)2=r2,解得r=5,然后利用面积法出AG,从而得到AF的长.
【解析】解:连接OA、OB,OB交AF于G,如图,
∵AB⊥CD,
∴AE=BE=AB=3,
设⊙O的半径为r,则OE=r﹣1,OA=r,
在Rt△OAE中,32+(r﹣1)2=r2,解得r=5,
∴OE=5﹣1=4,
∵=,
∴OB⊥AF,AG=FG,
∵AG OB=OE AB,
∴AG==,
∴AF=2AG=.
故答案为.
【点睛】本题考查了圆周角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理.
24.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
【点拨】(1)已知=得到AB=AC,又OC=OB,OA=OA,则△AOB≌△AOC,根据全等三角形的性质知,∠1=∠2,进而解答即可;
(2)根据勾股定理解答即可.
【解析】证明:(1)连接OB、OC,
∵=.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
【点睛】本题主要考查了全等三角形的判定和性质,利用圆中半径相等的隐含条件,获得全等的条件,从而利用全等的性质解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
3.4圆心角 同步分层作业
基础过关
1.如图,AB是⊙O的直径,==,若∠COD=35°,则∠AOE的度数是( )
A.35° B.55° C.75° D.95°
2.如图,点A,B,C,D是⊙O上的四个点,且AB=CD,OE⊥AB,OF⊥CD,则下列结论错误的是( )
A. B.OE=OF C.∠AOB=∠COD D.
3.在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.120° B.75° C.60° D.30°
4.已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆心角的度数为( )
A.45° B.90° C.90° 或270° D.45°或135°
5.如图,AB,CD是⊙O的直径,,若∠AOE=32°,则∠COE的度数是 .
6.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 .
7.如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为 ;∠A的度数为 .
8.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
9.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求、的度数.
10.如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F.且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
题组B 能力提升练
11.如图,在⊙O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD C.AB<2CD D.以上都不正确
12.如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F.若,AE=2,则⊙O的直径长为( )
A. B.8 C.10 D.
13.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
14.如图,在半径为10的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
A.6 B. C.8 D.
15.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°,AE交⊙O于点B,且AB=OD.则∠EOD= .
16.在半径为1的圆中,长度等于的弦所对的弧的度数为 .
17.如图,MN是⊙O的直径,MN=8,∠AMN=20°,点B为弧的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 .
18.如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于 .
19.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= .
20.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
21.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
22.如图,已知圆O的弦AB与直径CD交于点E,且CD平分AB.
(1)已知AB=6,EC=2,求圆O的半径;
(2)如果DE=3EC,求弦AB所对的圆心角的度数.
题组C 培优拔尖练
23.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
24.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
答案与解析
基础过关
1.如图,AB是⊙O的直径,==,若∠COD=35°,则∠AOE的度数是( )
A.35° B.55° C.75° D.95°
【点拨】由,可求得∠BOC=∠EOD=∠COD=35°,继而可求得∠AOE的度数.
【解析】解:∵,
∴∠BOC=∠EOD=∠COD=35°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=75°.
故选:C.
【点睛】此题考查了弧与圆心角的关系,掌握数形结合思想的应用是解题的关键.
2.如图,点A,B,C,D是⊙O上的四个点,且AB=CD,OE⊥AB,OF⊥CD,则下列结论错误的是( )
A. B.OE=OF C.∠AOB=∠COD D.
【点拨】根据圆心角、弧、弦的关系即可判断出答案.
【解析】解:A、∵AB=CD,∴=,故不符合题意;
B、∵OE⊥AB,OF⊥CD,
∴AE=AB,DF=CD,
∵AB=CD,
∴AE=DF,
∵OA=OD,
∴Rt△AOE≌Rt△DOF,
∴OE=OF,故不符合题意;
C、∵AB=CD,∴∠AOB=∠COD,故不符合题意;
D、根据已知条件得不到=,故符合题意.
故选:D.
【点睛】本题主要考查圆心角、弧、弦的关系和垂径定理,解题的关键是掌握在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.
3.在⊙O中,弦AB等于圆的半径,则它所对应的圆心角的度数为( )
A.120° B.75° C.60° D.30°
【点拨】连接OA、OB,如图,通过证明△OAB为等边三角形得到∠AOB=60°.
【解析】解:连接OA、OB,如图,
∵OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
即弦AB所对应的圆心角的度数为60°.
故选:C.
【点睛】本题考查了圆心角、弧、弦的关系,利用半径相等构建等腰三角形是解决问题的关键.
4.已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆心角的度数为( )
A.45° B.90° C.90° 或270° D.45°或135°
【点拨】根据弦AB把圆周分成1:3的两部分求出的度数,再根据圆心角的度数等于它所对的弧的度数求出答案即可.
【解析】解:∵弦AB把圆周分成1:3的两部分,
∴的度数是×360°=90°,
∴圆心角∠AOB的度数是90°或360°﹣90°=270°,
故选:C.
【点睛】本题考查了圆心角、弧、弦之间的关系,能求出的度数是解此题的关键.
5.如图,AB,CD是⊙O的直径,,若∠AOE=32°,则∠COE的度数是 64° .
【点拨】根据在同圆中,等弧所对的圆心角相等,可推出∠BOD=∠AOE=32°,再根据对顶角相等,可推出∠AOC=∠BOD=32°,最后用∠COE=∠COA+∠AOE即可求解.
【解析】解:∵,∠AOE=32°,
∴∠BOD=∠AOE=32°,
∵∠AOC=∠BOD=32°,
∴∠COE=∠COA+∠AOE=32°+32°=64°.
故答案为:64°.
【点睛】本题主要考查等弧和圆心角的关系,熟知在同圆中,等弧所对的圆心角相等,和对顶角相等是解题的关键.
6.如图,已知点C是⊙O的直径AB上的一点,过点C作弦DE,使CD=CO.若的度数为35°,则的度数是 105° .
【点拨】连接OD,OE,根据圆心角、弧、弦的关系定理求出∠AOD=35°,根据等腰三角形的性质和三角形内角和定理计算即可.
【解析】解:如图,连接OD,OE,
∵的度数为35°,
∴∠AOD=35°,
∵CD=CO,
∴∠ODC=∠AOD=35°,
∵OD=OE,
∴∠ODC=∠E=35°,
∴∠DOE=110°,
∴∠AOE=75°,
∴∠BOE=105°,
∴的度数是105°.
故答案为105°.
【点睛】本题考查的是圆心角、弧、弦的关系定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
7.如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,150°,则∠AOB的度数为 105° ;∠A的度数为 50° .
【点拨】根据量角器的知识,可直接求出∠AOB,连接OD,求出∠AOD,利用等腰三角形的性质可得∠A的度数.
【解析】解:
∵点C、D、A在量角器上对应读数分别为45°,70°,150°,
∴∠AOB=∠MOA﹣∠MOC=150°﹣45°=105°,
连接OD,则OA=OD,
∵∠AOD=150°﹣70°=80°,
∴∠A=(180°﹣80°)=50°.
故答案为:105°,50°.
【点睛】本题考查了圆周角定理的知识,解答本题的关键是掌握量角器的应用.
8.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
【点拨】根据圆心角、弧、弦之间的关系得出即可.
【解析】证明:∵AD=CB,
∴=,
∴+=+,
即=,
∴AB=CD.
【点睛】本题考查了圆心角、弧、弦之间的关系,能根据定理求出=是解此题的关键.
9.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求、的度数.
【点拨】连接CD,如图,利用互余计算出∠A=62°,则∠A=∠ADC=62°,再根据三角形内角和定理计算出∠ACD=56°,接着利用互余计算出∠DCE=34°,然后根据圆心角的度数等于它所对弧的度数求解.
【解析】解:连接CD,如图,
∵∠C=90°,∠B=28°,
∴∠A=90°﹣28°=62°,
∵CA=CD,
∴∠A=∠ADC=62°,
∴∠ACD=180°﹣2×62°=56°
∴的度数为56°;
∵∠DCE=90°﹣∠ACD=34°,
∴的度数为34°.
【点睛】本题考查的是圆心角、弧、弦的关系、等腰三角形的性质,掌握圆心角、弧、弦的关系定理是解题的关键.
10.如图,AB为⊙O的弦,半径OC,OD分别交AB于点E,F.且=.
(1)求证:AE=BF;
(2)作半径ON⊥AB于点M,若AB=12,MN=3,求OM的长.
【点拨】(1)连接OA、OB,证明△AOE≌△BOF(ASA),即可得出结论;
(2)连接OA,由垂径定理得出AM=AB=6,设OM=x,则OA=ON=x+3,在Rt△AOM中,由勾股定理得出方程,解方程即可.
【解析】(1)证明:连接OA、OB,如图1所示:
∵OA=OB,
∴∠A=∠B,
∵=,
∴∠AOE=∠BOF,
在△AOE和△OBF中,
,
∴△AOE≌△BOF(ASA),
∴AE=BF.
(2)解:连接OA,如图2所示:
∵OM⊥AB,
∴AM=AB=6,
设OM=x,则OA=ON=x+3,
在Rt△AOM中,由勾股定理得:62+x2=(x+3)2,
解得:x=4.5,
∴OM=4.5.
【点睛】本题考查垂径定理,勾股定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
题组B 能力提升练
11.如图,在⊙O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD C.AB<2CD D.以上都不正确
【点拨】首先取的中点E,连接AE,BE,由在⊙O中,=2,可证得==,即可得AE=BE=CD,然后由三角形的三边关系,求得答案.
【解析】解:取的中点E,连接AE,BE,
∵在⊙O中,=2,
∴==,
∴AE=BE=CD,
∵AE+BE>AB,
∴2CD>AB.
故选:C.
【点睛】此题考查了弧与弦的关系以及三角形的三边关系.注意在同圆或等圆中,同弧或等弧,所对的弦相等.
12.如图,AB为⊙O的直径,点D是的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F.若,AE=2,则⊙O的直径长为( )
A. B.8 C.10 D.
【点拨】连接OF,首先证明,设OA=OF=x,在Rt△OEF中,利用勾股定理构建方程即可解决问题.
【解析】解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,,
∵点D是弧AC的中点,
∴,
∴,
∴,
∴,
设OA=OF=x,
在Rt△OEF中,则有,
解得x=4,
∴AB=2x=8.
故选:B.
【点睛】本题考查勾股定理,垂径定理,弧,弦之间的关系等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
13.如图,⊙O在△ABC三边上截得的弦长相等,即DE=FG=MN,∠A=50°,则∠BOC=( )
A.100° B.110° C.115° D.120°
【点拨】过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,由于DE=FG=MN,所以弦的弦心距也相等,所以OB、OC是角平分线,可求出∠POQ,进而可求出∠BOC.
【解析】解:如图,过点O作OP⊥AB于点P,OQ⊥AC于点Q,OK⊥BC于点K,
∴∠APO=∠AQO=90°,
∵∠A=50°,
∴∠POQ=360°﹣90°﹣90°﹣50°=130°,
∵DE=FG=MN,
∴OP=OK=OQ,
∴OB、OC平分∠ABC和∠ACB,
∴∠BOC==115°.
故选:C.
【点睛】本题主要考查垂径定理,解题关键是构造出辅助线——弦心距.
14.如图,在半径为10的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=16,则OP的长为( )
A.6 B. C.8 D.
【点拨】作OM⊥AB于M,ON⊥CD于N,连接OB,OD,首先利用勾股定理求得OM的长,然后判定四边形OMPN是正方形,求得正方形的对角线的长即可求得OM的长.
【解析】解:作OM⊥AB于M,ON⊥CD于N,连接OB,OD,
由垂径定理、勾股定理得:OM=ON==6,
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=6.
故选:B.
【点睛】本题考查了垂径定理及勾股定理的知识,解题的关键是正确地作出辅助线.
15.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°,AE交⊙O于点B,且AB=OD.则∠EOD= 54° .
【点拨】连接OB,根据等腰三角形的性质求出∠A=∠BOA=18°,根据三角形外角性质求出∠EBO,根据等腰三角形的性质求出∠E,再根据三角形的外角性质求出答案即可.
【解析】解:连接OB,
∵AB=OD,OD=OB,
∴AB=OB,
∴∠BOA=∠A,
∵∠A=18°,
∴∠BOA=18°,
∴∠EBO=∠A+∠BOA=36°,
∵OE=OB,
∴∠E=∠EBO=36°,
∵∠A=18°,
∴∠EOD=∠A+∠E=18°+36°=54°,
故答案为:54°.
【点睛】本题考查了等腰三角形的性质和三角形的外角性质,能熟记等腰三角形的性质和三角形的外角性质是解此题的关键,注意:等边对等角,三角形的一个外角等于与它不相邻的两个内角的和.
16.在半径为1的圆中,长度等于的弦所对的弧的度数为 90°或270° .
【点拨】如图,⊙O的半径为1,弦AB=,连接OA、OB,利用勾股定理的逆定理可判断△OAB为等腰直角三角形,则∠AOB=90°,然后根据圆心角的度数等于它所对的弧的度数求解.
【解析】解:如图,⊙O的半径为1,弦AB=,
连接OA、OB,
∵OA=OB=1,
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,
∴∠AOB=90°,
∴AB所所的弧的度数为90°或270°.
故答案为90°或270°.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
17.如图,MN是⊙O的直径,MN=8,∠AMN=20°,点B为弧的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 4 .
【点拨】过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,由对称的性质可知=,再由圆周角定理可求出∠A′ON的度数,再由勾股定理即可求解.
【解析】解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,
连接OB,OA′,AA′,
∵AA′关于直线MN对称,
∴=,
∵∠AMN=20°,
∴∠A′ON=40°,∠BON=20°,
∴∠A′OB=60°,
∴△A′OB是等边三角形,
∴A′B=MN=4,即PA+PB的最小值4.
故答案为:4.
【点睛】本题考查的是圆心角、弧、弦的关系及轴对称﹣最短路线问题,解答此题的关键是根据题意作出辅助线,构造出直角三角形,利用勾股定理求解.
18.如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD,已知DE=6,∠BAC+∠EAD=180°,则圆心A到弦BC的距离等于 3 .
【点拨】作AH⊥BC于H,作直径CF,连接BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=BF=3.
【解析】解:作AH⊥BC于H,作直径CF,连接BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴=,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵CA=AF,
∴AH为△CBF的中位线,
∴AH=BF=3.
∴点A到弦BC的距离为:3.
解法二:如图,过点A作AM⊥BC于M,AN⊥DE于N.
∵AM⊥BC,AN⊥DE,
∴CM=MB,DN=NE=3,
∵AC=AB=AD=AE,
∴∠BAC=2∠MAC,∠EAD=2∠DAN,
∵∠BAC+∠EAD=180°,
∴2∠CAM+2∠DAN=180°,
∴∠CAM+∠DAN=90°,
∵∠ACM+∠CAM=90°,
∴∠ACM=∠DAN,
∵∠AMC=∠AND=90°,
∴△AMC≌△DNA(AAS),
∴AM=DN=3,
故答案为:3.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和三角形中位线性质.
19.如图,AB,CD是⊙O的两条弦,M,N分别为AB,CD的中点,且∠AMN=∠CNM,AB=6,则CD= 6 .
【点拨】连接OM,ON,OA,OC,先根据垂径定理得出AM=AB,CN=CD,再由∠AMN=∠CNM得出∠NMO=∠MNO,即OM=ON,再由OA=OC可知Rt△AOM≌Rt△CON,故AM=CN,由此即可得出结论.
【解析】解:连接OM,ON,OA,OC,
∵M、N分别为AB、CD的中点,
∴OM⊥AB,ON⊥CD,
∴AM=AB,CN=CD,
∵∠AMN=∠CNM,
∴∠NMO=∠MNO,即OM=ON,
在Rt△AOM与Rt△CON中,
,
∴Rt△AOM≌Rt△CON(HL),
∴AM=CN,
∴AB=CD=6.
故答案为:6.
【点睛】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
20.如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求的度数;
(2)若BC=9,AC=12,求BD的长.
【点拨】(1)求出∠B的度数,求出∠B所对的弧的度数,即可得出答案;
(2)根据勾股定理求出AB,根据割线定理得出比例式,即可得出答案.
【解析】解:(1)连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴∠DCE=40°,
∴的度数为40°;
(2)延长AC交⊙C与点F,
∵∠BCA=90°,CF=BC=9,AC=12,
∴AB=,AE=12﹣9=3.AF=AC+CF=12+9=21,
∵AB与AF均是⊙C的割线,
∴AD AB=AE AF,即15AD=3×21,解得AD=,
∴BD=AB﹣AD=15﹣=.
【点睛】本题考查了勾股定理,割线定理圆心角、弧、弦之间的关系,切割线定理的应用,能综合运用知识点进行计算是解此题的关键.
21.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
【点拨】(1)欲证明AB=CD,只需证得=;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.构建正方形EFOG,利用正方形的性质,垂径定理和勾股定理来求AF的长度,则易求AE的长度.
【解析】(1)证明:如图,∵AD=BC,
∴=,
∴﹣=﹣,即=
∴AB=CD;
(2)解:如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.
【点睛】本题考查了勾股定理,正方形的判定与性质,垂径定理以及圆周角、弧、弦间的关系.注意(2)中辅助线的作法.
22.如图,已知圆O的弦AB与直径CD交于点E,且CD平分AB.
(1)已知AB=6,EC=2,求圆O的半径;
(2)如果DE=3EC,求弦AB所对的圆心角的度数.
【点拨】(1)连接OA,如图,设⊙O的半径为r,则OA=r,OE=r﹣2,先根据垂径定理得到AE=BE=3,CD⊥AB,在Rt△OAE中利用勾股定理得到32+(r﹣2)2=r2,然后解方程即可;
(2)连接OB,如图,先利用DE=3EC得到OE=CE,即OE=OA,再利用正弦的定义得到∠A=30°,然后根据等腰三角形的性质和三角形内角和定理计算∠AOB即可.
【解析】解:(1)连接OA,如图,设⊙O的半径为r,则OA=r,OE=r﹣2,
∵CD平分AB,
∴AE=BE=3,CD⊥AB,
在Rt△OAE中,32+(r﹣2)2=r2,
解得r=,
即⊙O的半径为;
(2)连接OB,如图,
∵DE=3EC,
∴OC+OE=3EC,
即OE+CE+OE=3CE,
∴OE=CE,
∴OE=OC=OA,
在Rt△OAE中,∵sinA==,
∴∠A=30°,
∵OA=OB,
∴∠B=∠A=30°,
∴∠AOB=180°﹣∠A﹣∠B=120°,
即弦AB所对的圆心角的度数为120°.
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理和勾股定理.
题组C 培优拔尖练
23.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为 .
【点拨】连接OA、OB,OB交AF于G,如图,利用垂径定理得到AE=BE=3,设⊙O的半径为r,则OE=r﹣1,OA=r,根据勾股定理得到32+(r﹣1)2=r2,解得r=5,然后利用面积法出AG,从而得到AF的长.
【解析】解:连接OA、OB,OB交AF于G,如图,
∵AB⊥CD,
∴AE=BE=AB=3,
设⊙O的半径为r,则OE=r﹣1,OA=r,
在Rt△OAE中,32+(r﹣1)2=r2,解得r=5,
∴OE=5﹣1=4,
∵=,
∴OB⊥AF,AG=FG,
∵AG OB=OE AB,
∴AG==,
∴AF=2AG=.
故答案为.
【点睛】本题考查了圆周角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理.
24.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
【点拨】(1)已知=得到AB=AC,又OC=OB,OA=OA,则△AOB≌△AOC,根据全等三角形的性质知,∠1=∠2,进而解答即可;
(2)根据勾股定理解答即可.
【解析】证明:(1)连接OB、OC,
∵=.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
【点睛】本题主要考查了全等三角形的判定和性质,利用圆中半径相等的隐含条件,获得全等的条件,从而利用全等的性质解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
