浙教版初中数学八年级上册 2.6直角三角形(2) 课件
文档属性
| 名称 | 浙教版初中数学八年级上册 2.6直角三角形(2) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-30 18:45:44 | ||
图片预览




文档简介
课件23张PPT。?
2.5 直角三角形(二) 1.直角三角形的两个锐角互余.
2.有两个角互余的三角形是直角三角形.
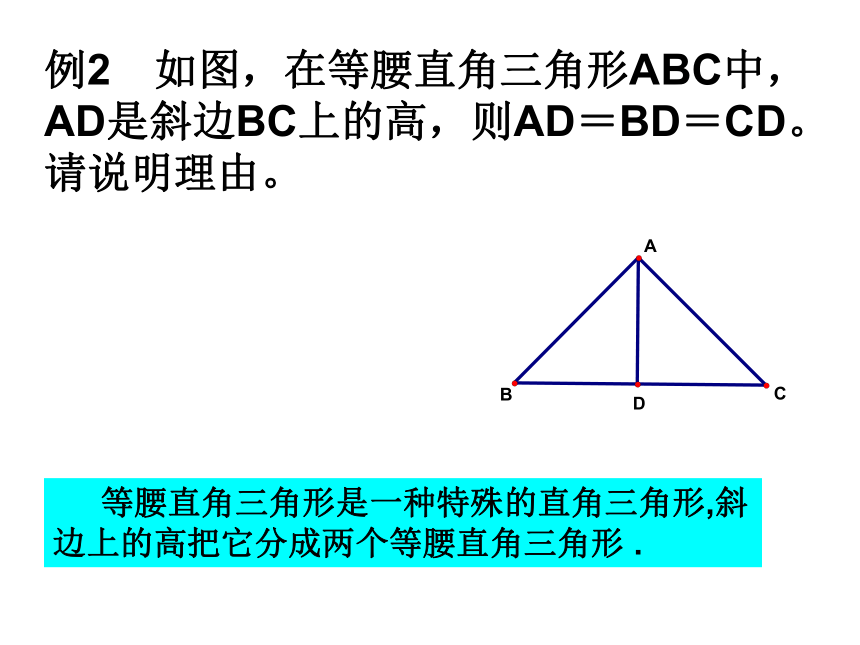
3.等腰直角三角形的两个锐角都是45゜复习上节课学习的直角三角形知识:例2 如图,在等腰直角三角形ABC中,
AD是斜边BC上的高,则AD=BD=CD。
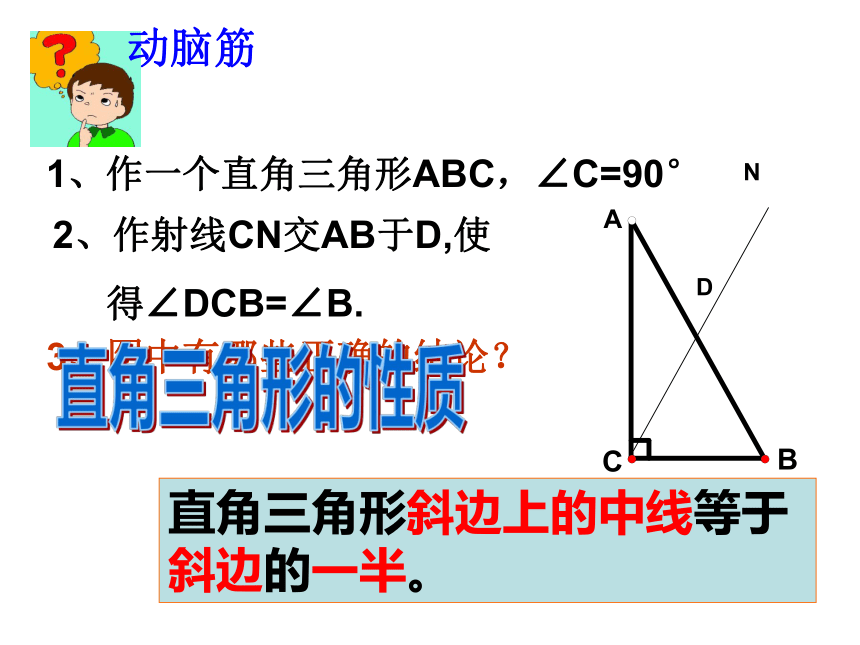
请说明理由。 等腰直角三角形是一种特殊的直角三角形,斜边上的高把它分成两个等腰直角三角形 .动脑筋1、作一个直角三角形ABC,∠C=90°2、作射线CN交AB于D,使
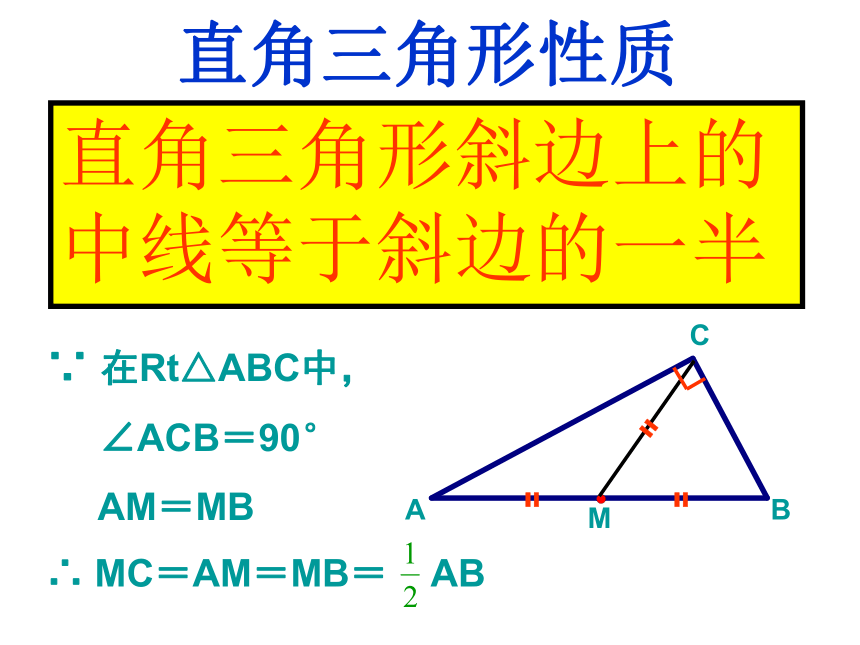
得∠DCB=∠B.ND3、图中有哪些正确的结论?直角三角形斜边上的中线等于斜边的一半。直角三角形的性质操作:①任意画一个直角三角形;②画出斜边上的中线;③利用圆规比较中线与斜边的一半的长短。 AMBC●●〓〓〓▲▲▲探 索 一 下结论:斜边上的中线等于斜边的一半。 证明: 注意:以后还会有更简单的证法。直角三角形性质直角三角形斜边上的中线等于斜边的一半AMBC〓〓〓∵ 在Rt△ABC中,
∠ACB=90°
AM=MB∴ MC=AM=MB= AB (1)直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为 。
(2)已知,在Rt△ABC中,BD为斜边AC上的中线,若∠A=35°,那么∠DBC= 。455°练一练:1、已知Rt△ABC中,斜边AB=10cm,则斜边上
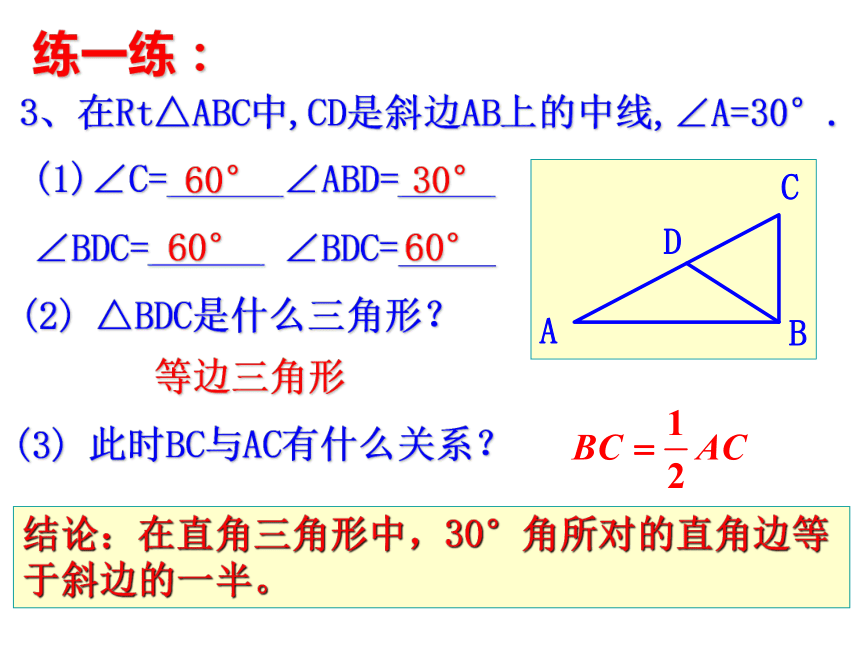
的中线的长为______2、如图,在Rt△ABC中,CD是斜边AB上的中线,∠CDA=80°,则∠A=_____ ∠B=_____5cm50°40°练一练:3、在Rt△ABC中,CD是斜边AB上的中线,∠A=30°.(1)∠C=______∠ABD=_____
∠BDC=______ ∠BDC=_____(2) △BDC是什么三角形?(3) 此时BC与AC有什么关系?等边三角形结论:在直角三角形中,30°角所对的直角边等于斜边的一半。60°30°60°60°例1:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。说明两条线段相等,有时还可以通过第三条线段进行等量代换。回顾:2、在直角三角形中,30°角
所对的直角边等于斜边的一半。1、直角三角形斜边上
的中线等于斜边的一半。例1、如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少m? 30°AB〓〓〓 30° 60° 60°AC=DC= AB=100m课 内 练 习1、已知在Rt△ABC,斜边上的中线CD=5cm ,则斜边AB的长是多少?2、如图是一副三角尺拼成的四边形ABCD,E是BD的中点,点E与A,C的距离相等吗?请说明理由。ABCDE●在直角三角形中,如果一个锐角是30°,则它所对的直角边等于斜边的一半。 30°在直角三角形中,如果一条直角边等于斜边的一半,则这条直角边所对的锐角是30°。 60°〓ABCDEO如图,已知△ABC为等边三角形,AD为高,DE⊥AC,请说明AC=4CE的理由。 如图,已知∠AOB=30°,OC平分∠AOB,P为OC上一点且PD∥OA交OB于D,PE⊥OA,若OD=4,试求PE的长。PABCDEF〓〓▲▲例1、如图,已知AD⊥BD,AC⊥BC,E为AB的中点,F为DC的中点,试证EF⊥DC。分析:两个直角三角形,思路:须证ED=EC,利用“三线合一”斜边上的中线;例2、如图,在Rt△ABC中,CD是斜边AB上的中线,且CD= AB,△ABC是直角三角形吗?请说明理由。ABCD〓〓〓●▲●▲在三角形中,若一边上的中线等于这边的一半,则三角形为直角三角形作 业 题 1、已知直角三角形斜边长为10cm ,求斜边上的中线的长?2、如图,在Rt△ABC中,CD是斜边AB上的中线,∠CDA=80°,求∠A,∠B的度数?ABCD〓〓 80°〓5cm∠A=50°∠B=40°3、如图,一太阳能热水器受光面的一边AB长为1.5米,中∠ACB=90°,倾斜角∠ABC=30°,连杆CD经过AB的中点D,求支架AC,连杆CD的长。ABCD〓〓 30°〓例3:如图,它是人字屋架设计图,其中AB=AC=5米。D是AB的中点,AE⊥BC。如果∠BAC=120゜, 求AE和DE的长度。体会·分享1.直角三角形斜边上的中线
等于斜边的一半。2.在直角三角形中,30°角所对的直角边等于斜边的一半。今日回家作业与预习作业(A)《教与学》第1—8,10、11题;
(B)《教与学》第9、12题。
预习作业:
课本第40页《课内练习》第1题;
《作业题》第1、3题。
2.5 直角三角形(二) 1.直角三角形的两个锐角互余.
2.有两个角互余的三角形是直角三角形.
3.等腰直角三角形的两个锐角都是45゜复习上节课学习的直角三角形知识:例2 如图,在等腰直角三角形ABC中,
AD是斜边BC上的高,则AD=BD=CD。
请说明理由。 等腰直角三角形是一种特殊的直角三角形,斜边上的高把它分成两个等腰直角三角形 .动脑筋1、作一个直角三角形ABC,∠C=90°2、作射线CN交AB于D,使
得∠DCB=∠B.ND3、图中有哪些正确的结论?直角三角形斜边上的中线等于斜边的一半。直角三角形的性质操作:①任意画一个直角三角形;②画出斜边上的中线;③利用圆规比较中线与斜边的一半的长短。 AMBC●●〓〓〓▲▲▲探 索 一 下结论:斜边上的中线等于斜边的一半。 证明: 注意:以后还会有更简单的证法。直角三角形性质直角三角形斜边上的中线等于斜边的一半AMBC〓〓〓∵ 在Rt△ABC中,
∠ACB=90°
AM=MB∴ MC=AM=MB= AB (1)直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为 。
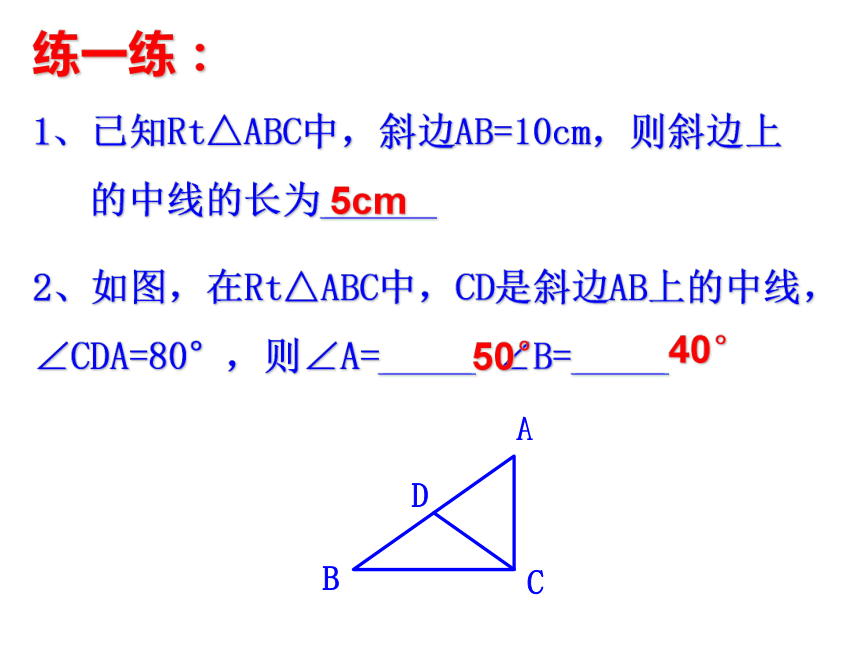
(2)已知,在Rt△ABC中,BD为斜边AC上的中线,若∠A=35°,那么∠DBC= 。455°练一练:1、已知Rt△ABC中,斜边AB=10cm,则斜边上
的中线的长为______2、如图,在Rt△ABC中,CD是斜边AB上的中线,∠CDA=80°,则∠A=_____ ∠B=_____5cm50°40°练一练:3、在Rt△ABC中,CD是斜边AB上的中线,∠A=30°.(1)∠C=______∠ABD=_____
∠BDC=______ ∠BDC=_____(2) △BDC是什么三角形?(3) 此时BC与AC有什么关系?等边三角形结论:在直角三角形中,30°角所对的直角边等于斜边的一半。60°30°60°60°例1:如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。说明两条线段相等,有时还可以通过第三条线段进行等量代换。回顾:2、在直角三角形中,30°角
所对的直角边等于斜边的一半。1、直角三角形斜边上
的中线等于斜边的一半。例1、如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑行至B。已知AB=200m,问这名滑雪运动员的高度下降了多少m? 30°AB〓〓〓 30° 60° 60°AC=DC= AB=100m课 内 练 习1、已知在Rt△ABC,斜边上的中线CD=5cm ,则斜边AB的长是多少?2、如图是一副三角尺拼成的四边形ABCD,E是BD的中点,点E与A,C的距离相等吗?请说明理由。ABCDE●在直角三角形中,如果一个锐角是30°,则它所对的直角边等于斜边的一半。 30°在直角三角形中,如果一条直角边等于斜边的一半,则这条直角边所对的锐角是30°。 60°〓ABCDEO如图,已知△ABC为等边三角形,AD为高,DE⊥AC,请说明AC=4CE的理由。 如图,已知∠AOB=30°,OC平分∠AOB,P为OC上一点且PD∥OA交OB于D,PE⊥OA,若OD=4,试求PE的长。PABCDEF〓〓▲▲例1、如图,已知AD⊥BD,AC⊥BC,E为AB的中点,F为DC的中点,试证EF⊥DC。分析:两个直角三角形,思路:须证ED=EC,利用“三线合一”斜边上的中线;例2、如图,在Rt△ABC中,CD是斜边AB上的中线,且CD= AB,△ABC是直角三角形吗?请说明理由。ABCD〓〓〓●▲●▲在三角形中,若一边上的中线等于这边的一半,则三角形为直角三角形作 业 题 1、已知直角三角形斜边长为10cm ,求斜边上的中线的长?2、如图,在Rt△ABC中,CD是斜边AB上的中线,∠CDA=80°,求∠A,∠B的度数?ABCD〓〓 80°〓5cm∠A=50°∠B=40°3、如图,一太阳能热水器受光面的一边AB长为1.5米,中∠ACB=90°,倾斜角∠ABC=30°,连杆CD经过AB的中点D,求支架AC,连杆CD的长。ABCD〓〓 30°〓例3:如图,它是人字屋架设计图,其中AB=AC=5米。D是AB的中点,AE⊥BC。如果∠BAC=120゜, 求AE和DE的长度。体会·分享1.直角三角形斜边上的中线
等于斜边的一半。2.在直角三角形中,30°角所对的直角边等于斜边的一半。今日回家作业与预习作业(A)《教与学》第1—8,10、11题;
(B)《教与学》第9、12题。
预习作业:
课本第40页《课内练习》第1题;
《作业题》第1、3题。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
