浙教版初中数学八年级上册 2.4等腰三角形的判定 课件
文档属性
| 名称 | 浙教版初中数学八年级上册 2.4等腰三角形的判定 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 258.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-30 18:51:44 | ||
图片预览


文档简介
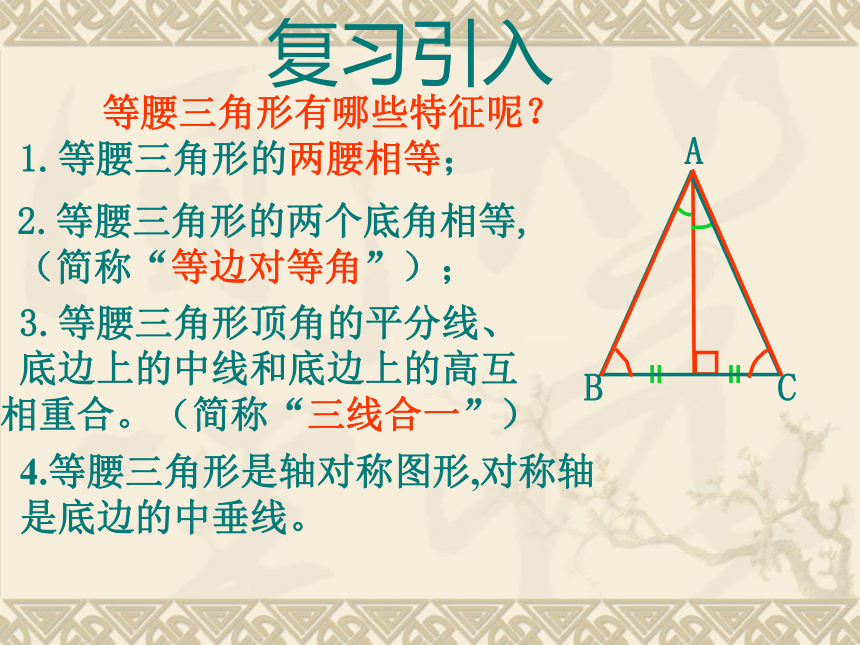
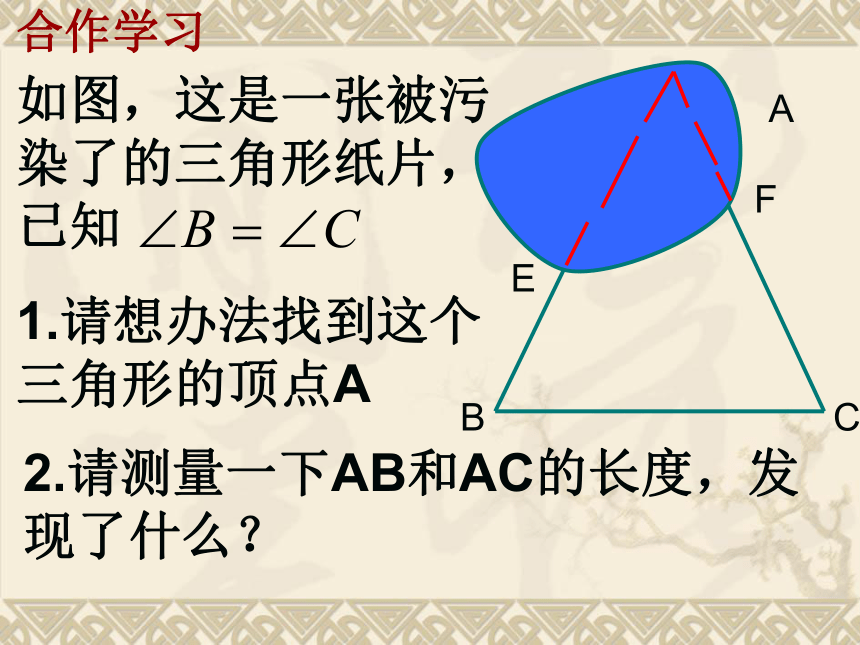
课件16张PPT。2.3等腰三角形的判定复习引入1.等腰三角形的两腰相等;2.等腰三角形的两个底角相等,(简称“等边对等角”);3.等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合。(简称“三线合一”)4.等腰三角形是轴对称图形,对称轴是底边的中垂线。如图,这是一张被污染了的三角形纸片,已知
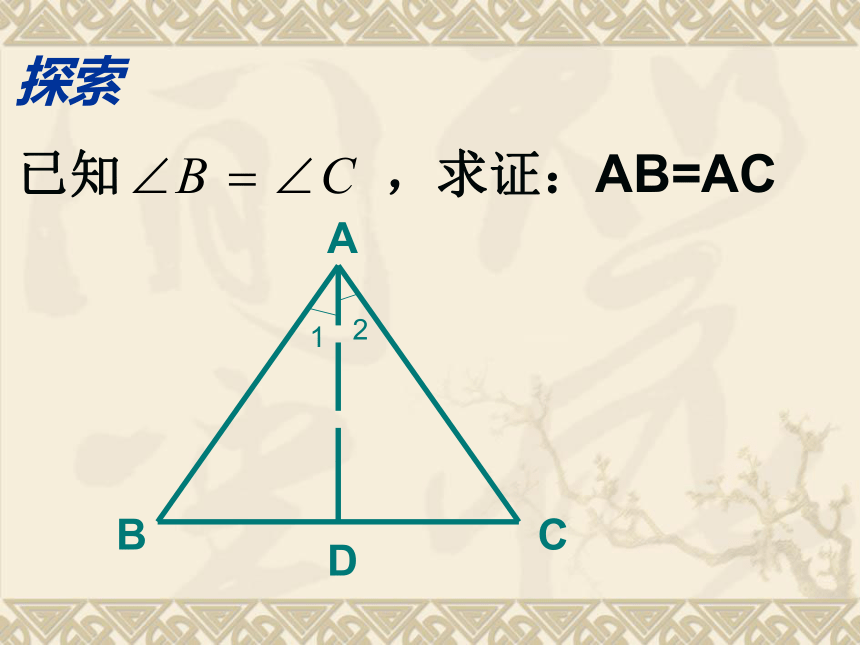
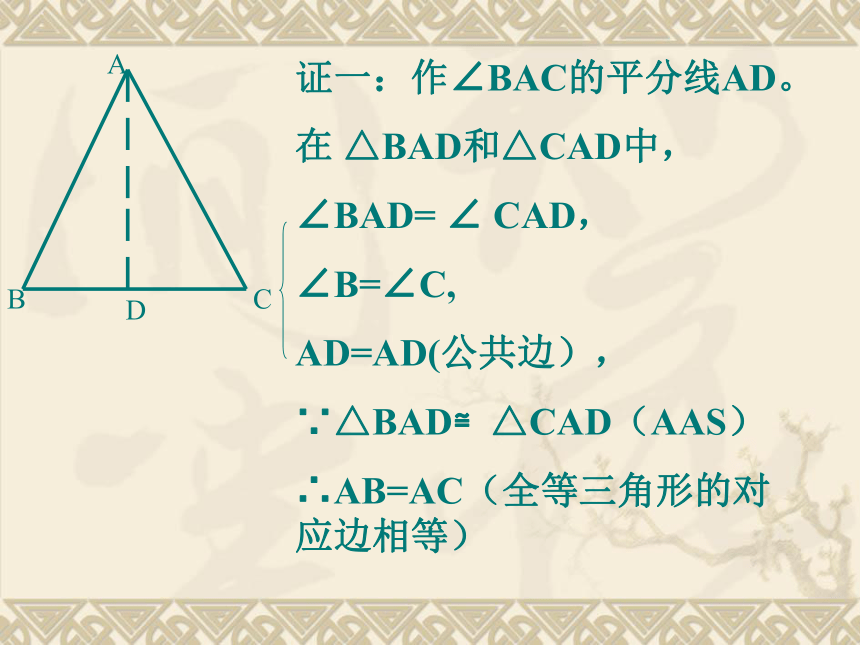
1.请想办法找到这个三角形的顶点A2.请测量一下AB和AC的长度,发现了什么?合作学习探索证一:作∠BAC的平分线AD。
在 △BAD和△CAD中,
∠BAD= ∠ CAD,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS)
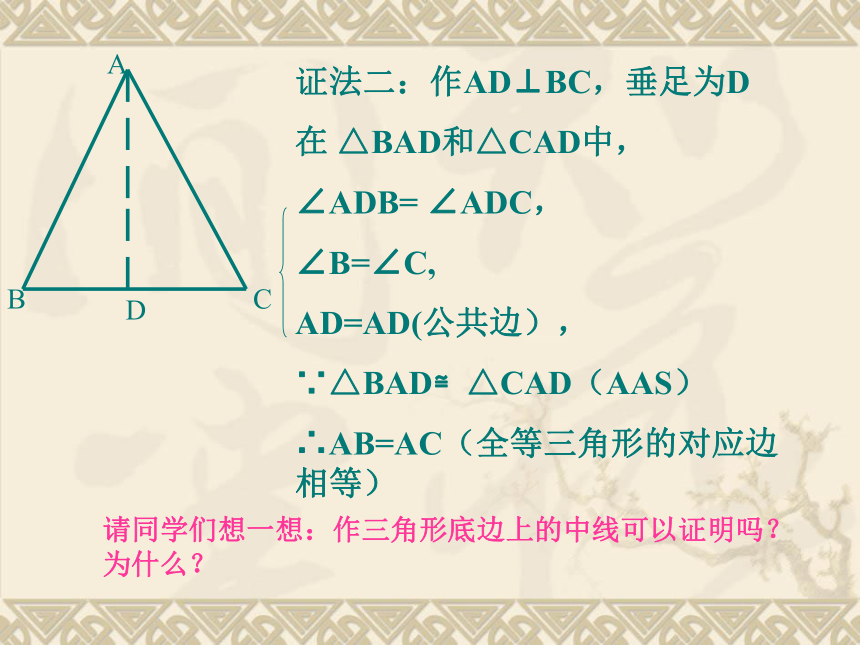
∴AB=AC(全等三角形的对应边相等)证法二:作AD⊥BC,垂足为D
在 △BAD和△CAD中,
∠ADB= ∠ADC,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS)
∴AB=AC(全等三角形的对应边相等)请同学们想一想:作三角形底边上的中线可以证明吗?为什么?等腰三角形的判定: 如果一个三角形有
两个角相等,那么这个
三角形是等腰三角形。
即:在同一个三角形中,
等角对等边例2:上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°求从B处到灯塔C的距离NBAC80°40°北解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里练习在△ABC中,∠A=50°,当∠B的度数= 时,△ABC是等腰三角形.①∠A是顶角,∠B=(180°-∠A)÷2=65°;
②∠A是底角,∠B=∠A=50°.
③∠A是底角,∠A=∠C=50°,则∠B=180°-50°×2=80°,
∴当∠B的度数为50°或65°或80°时,△ABC是等腰三角形.50°或65°或80°例:如图,已知△ABC中,AB=AC,D、E分别是AB和BC上的点,连接DE并延长与AC的延长线交于点F,若DE=EF,求证:BD=CF.证明:过D作DG∥AF交BC于G,如图,
则∠F=∠GDE,DE=EF,∠DEG=∠FEC
∴△DGE≌△FCE(ASA),
∴GD=CF,
∵AB=AC,
∴∠B=∠ACB,
又∵DG∥AF,
∴∠ACB=∠BGD,
∴∠B=∠BGD,
∴BD=GD,
又∵GD=CF,
∴BD=CF.已知如图,在△ABC中,AD平分∠BAC交BC于D,E为AD延长线上一点且∠ACE=∠B.求证:CD=CE.∵在△ABC中,AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠CDE=∠ADB=180°-∠B-∠BAD,∠E=180°-∠CAD-∠ACE,
又∵∠ACE=∠B,
∴∠CDE=∠E,
∴CD=CE.如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.∵AB=AC,∴∠ABC=∠C,
又BC=BD,∴∠BDC=∠C,∴∠DBC=∠A,
∵AD=DE=EB,∴∠A=∠AED,∠EDB=∠EBD,
∴∠A=2∠DBE,即∠ABC=3∠DBE,
∵∠A+2∠C=180°,
∴2∠DBE+2∠ABC=180°,
∴2∠DBE+2×(3∠DBE)=180°,
即8∠DBE=180°,
∠A=2∠DBE=45°.例:在Rt △ABC中, ∠CBA=90°,D为AB延长线上的一点,E在BC上,连结DE延长交AC于点F,且EF=FC,求证:AF=DF。例:在△ABC中, ∠ABC和∠ACB的平分线交于点O,过点O作EF//BC,交AB于点O,交AC于点F。若AB=8,AC=6,求△AEF的周长。小结有两边相等的三角形是等腰三角形。2.等边对等角,3. 三线合一。4.是轴对称图形.2.等角对等边,1.两边相等。1.两腰相等.
1.请想办法找到这个三角形的顶点A2.请测量一下AB和AC的长度,发现了什么?合作学习探索证一:作∠BAC的平分线AD。
在 △BAD和△CAD中,
∠BAD= ∠ CAD,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS)
∴AB=AC(全等三角形的对应边相等)证法二:作AD⊥BC,垂足为D
在 △BAD和△CAD中,
∠ADB= ∠ADC,
∠B=∠C,
AD=AD(公共边),
∵△BAD≌△CAD(AAS)
∴AB=AC(全等三角形的对应边相等)请同学们想一想:作三角形底边上的中线可以证明吗?为什么?等腰三角形的判定: 如果一个三角形有
两个角相等,那么这个
三角形是等腰三角形。
即:在同一个三角形中,
等角对等边例2:上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°, ∠NBC=80°求从B处到灯塔C的距离NBAC80°40°北解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C40海里练习在△ABC中,∠A=50°,当∠B的度数= 时,△ABC是等腰三角形.①∠A是顶角,∠B=(180°-∠A)÷2=65°;
②∠A是底角,∠B=∠A=50°.
③∠A是底角,∠A=∠C=50°,则∠B=180°-50°×2=80°,
∴当∠B的度数为50°或65°或80°时,△ABC是等腰三角形.50°或65°或80°例:如图,已知△ABC中,AB=AC,D、E分别是AB和BC上的点,连接DE并延长与AC的延长线交于点F,若DE=EF,求证:BD=CF.证明:过D作DG∥AF交BC于G,如图,
则∠F=∠GDE,DE=EF,∠DEG=∠FEC
∴△DGE≌△FCE(ASA),
∴GD=CF,
∵AB=AC,
∴∠B=∠ACB,
又∵DG∥AF,
∴∠ACB=∠BGD,
∴∠B=∠BGD,
∴BD=GD,
又∵GD=CF,
∴BD=CF.已知如图,在△ABC中,AD平分∠BAC交BC于D,E为AD延长线上一点且∠ACE=∠B.求证:CD=CE.∵在△ABC中,AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠CDE=∠ADB=180°-∠B-∠BAD,∠E=180°-∠CAD-∠ACE,
又∵∠ACE=∠B,
∴∠CDE=∠E,
∴CD=CE.如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.∵AB=AC,∴∠ABC=∠C,
又BC=BD,∴∠BDC=∠C,∴∠DBC=∠A,
∵AD=DE=EB,∴∠A=∠AED,∠EDB=∠EBD,
∴∠A=2∠DBE,即∠ABC=3∠DBE,
∵∠A+2∠C=180°,
∴2∠DBE+2∠ABC=180°,
∴2∠DBE+2×(3∠DBE)=180°,
即8∠DBE=180°,
∠A=2∠DBE=45°.例:在Rt △ABC中, ∠CBA=90°,D为AB延长线上的一点,E在BC上,连结DE延长交AC于点F,且EF=FC,求证:AF=DF。例:在△ABC中, ∠ABC和∠ACB的平分线交于点O,过点O作EF//BC,交AB于点O,交AC于点F。若AB=8,AC=6,求△AEF的周长。小结有两边相等的三角形是等腰三角形。2.等边对等角,3. 三线合一。4.是轴对称图形.2.等角对等边,1.两边相等。1.两腰相等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
