1.3 解直角三角形（1）

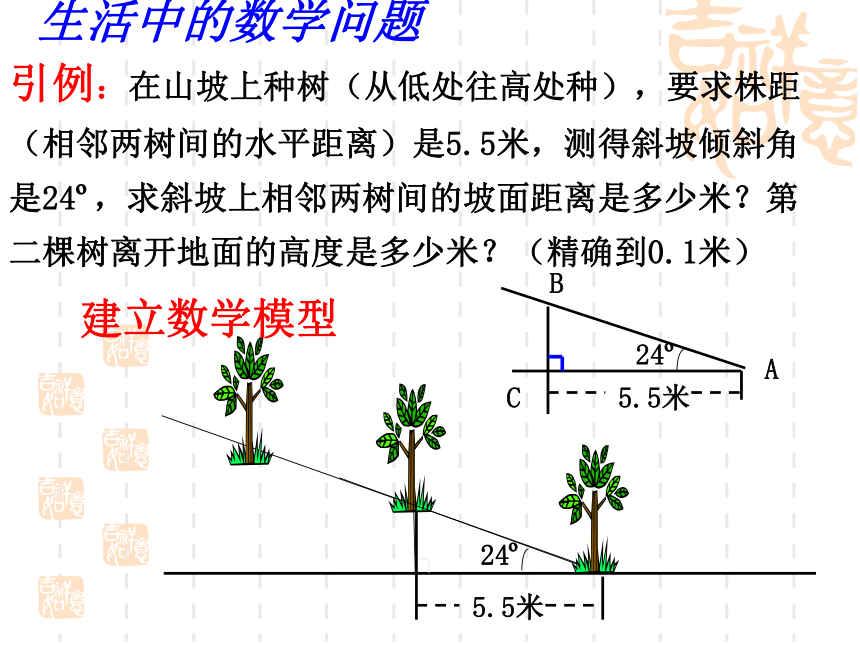
课件13张PPT。1.3解直角三角形(1)引例：在山坡上种树（从低处往高处种），要求株距（相邻两树间的水平距离）是5.5米，测得斜坡倾斜角是24o，求斜坡上相邻两树间的坡面距离是多少米？第二棵树离开地面的高度是多少米？（精确到0.1米） 生活中的数学问题建立数学模型在直角三角形中共有五个元素：
边a,b,c, 锐角∠A,∠B.这五个元素之间有如下等量关系：
(1)三边之间关系：a2 +b2 =c2 (勾股定理) (2)锐角之间关系：∠A+∠B=90°(3)边角之间关系：请记住这些结论例1、如图，在Rt△ABC中，∠C=900，∠A=500，AB=3，求a，b 和∠B 。（边长保留2个有效数字）解：Rt△ABC中∠B=900-∠A=400∴a=AB×sinA=3×sin500≈2.3∴b=AB×cosA=3×cos500≈1.9 在直角三角形中，由已知的一些边、角求出另一些边、角的过程，叫做解直角三角形。定义： 在直角三角形中，已知几个元素
就可以求出其它元素呢？ 在直角三角形中，已知几个元素就可以求出其它元素呢？解直角三角形，只有下面两种情况：
（1）已知两条边；
（2）已知一条边和一个锐角
练一练1、已知在Rt△ABC中，∠C= Rt∠，a,b,c分别是∠A ,∠B, ∠C的对边，根据下列条件解直角三角形（边长保留2个有效数字，角度精确到10)
(1)c=10, ∠A =30o (2)b=4, ∠B=72o
(3)a=5, c=7 （4）a=20,2、 已知在Rt△ABC中， ∠C= Rt∠ ， a=5,∠B=54033’，求∠A和b,c (边长保留2个
有效数字）。
解:在Rt△ABD中,∴α≈350.答:斜面钢条a的长度约为6.1米,坡角约为350.例2、如图是某市“平改坡”工程中一种坡屋顶设计，已知平顶屋面的宽度L为10m，坡屋顶的设计高度h为3.5m，求斜面钢条a的长度和坡角a。（长度精确到0.1米，角度精确到1°）挑战自我1.已知，在△ABC中,∠B=45°,AC=4,
， , 求BC的值。
构造直角三角形分类讨论思想说一说1，定义：解直角三角形
解直角三角形中，有下面两种情况：
（1）已知两条边；
（2）已知一条边和一个锐角.
2，直角三角形中的五个元素之间关系：
3，解直角三角形中的几个注意:

（1）有斜用弦，无斜用切，宁乘勿除，取原避中。
（2）数形结合，利于分析。（4）实际问题数学化.(数学建模思想)
（5）全面地看问题。（分类讨论思想）
（3）构造直角三角形.1，在直角三角形中共有五个元素：边a,b,c, 锐角∠A,∠B.这五个元素之间有如下等量关系：
(1)三边之间关系：a2 +b2 =c2 (勾股定理) (2)锐角之间关系：∠A+∠B=90°(3)边角之间关系：请记住这些结论再 见