1.3解直角三角形(3)
图片预览


文档简介
课件27张PPT。1.3 解直角三角形(3)浙教版九下第一章回顾2.精确度:
边长保留四个有效数字,角度精确到1′.3.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角1.解直角三角形.
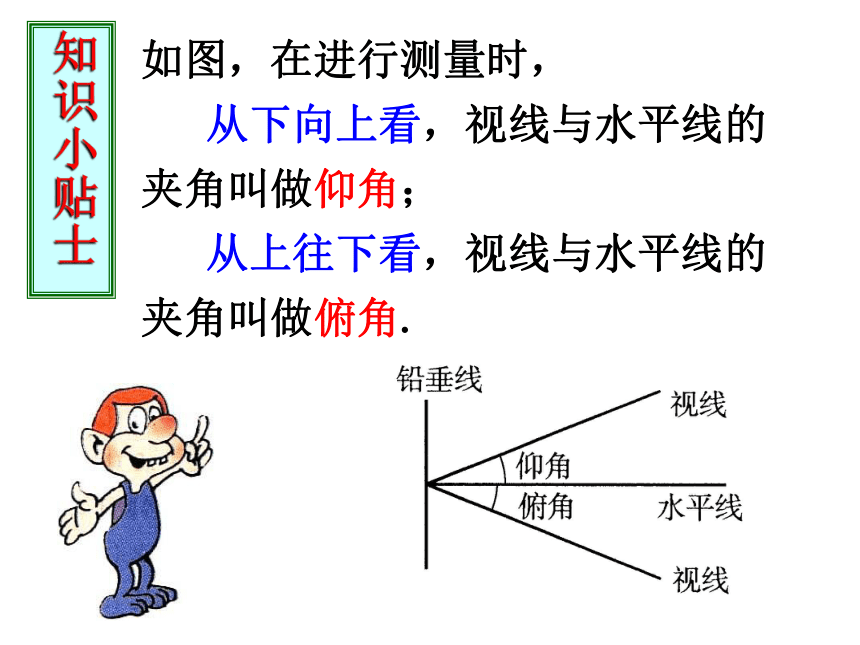
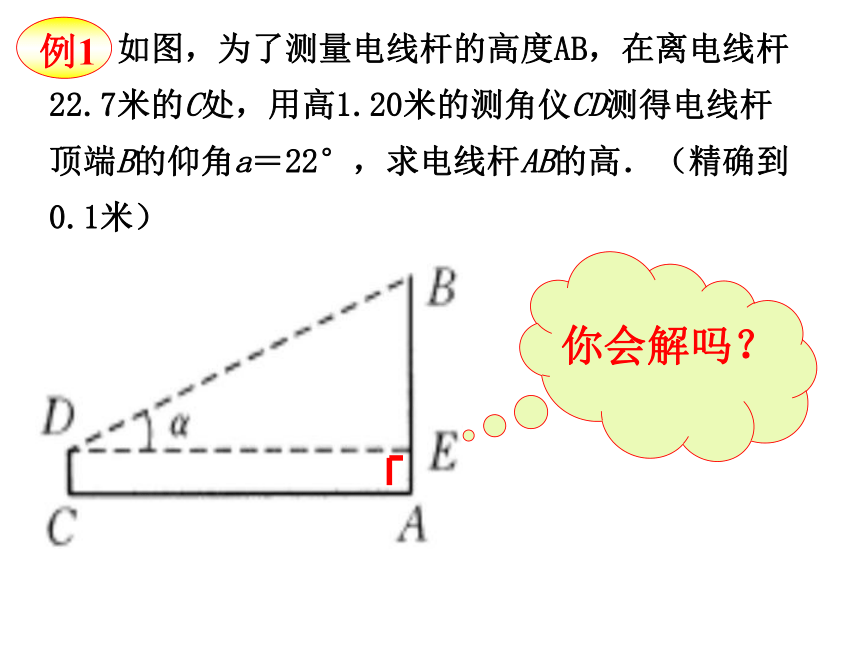
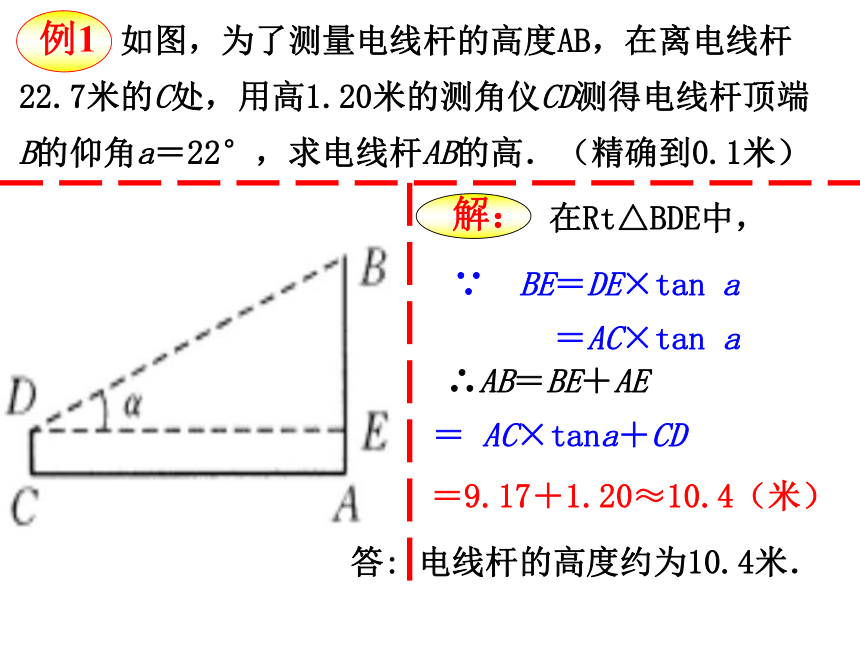
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.如图,在进行测量时, 从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角. 知识小贴士例1 如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)在Rt△BDE中, 如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)答: 电线杆的高度约为10.4米.=9.17+1.20≈10.4(米)= AC×tana+CD ∴AB=BE+AE ∵ BE=DE×tan a
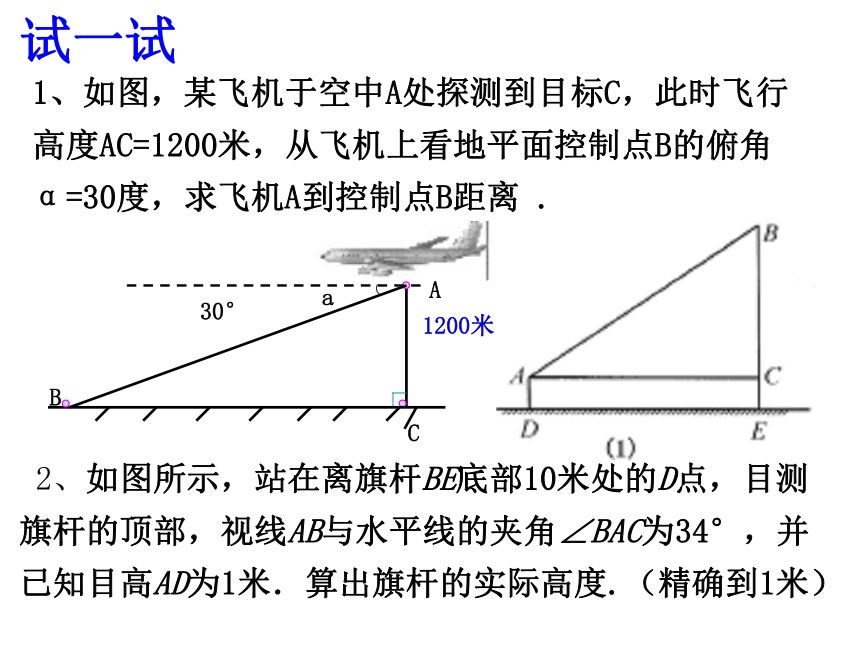
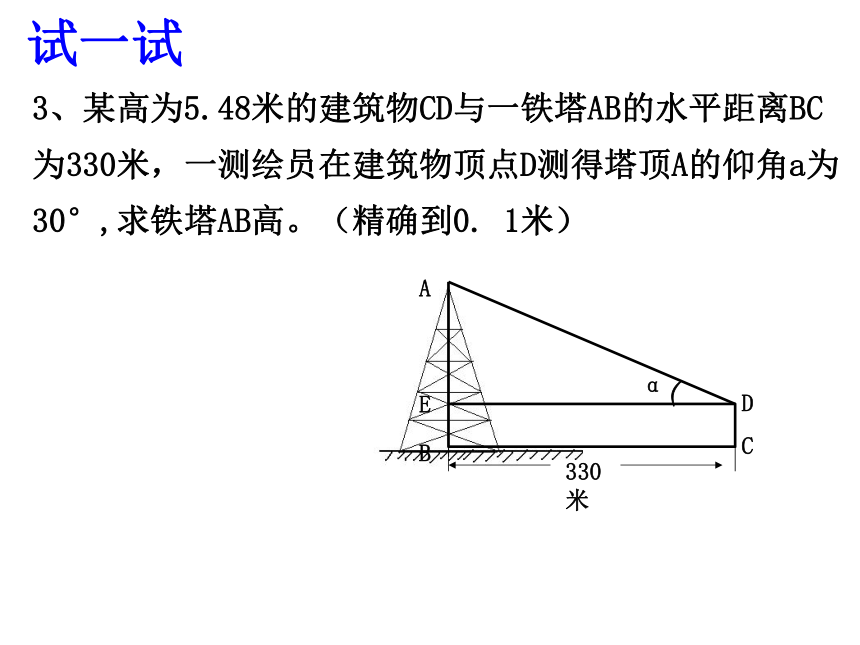
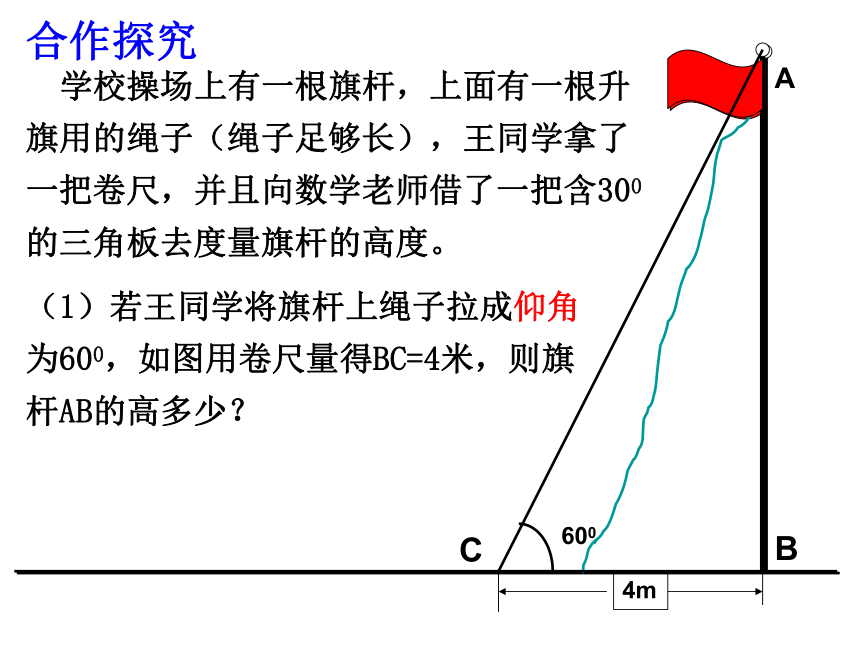
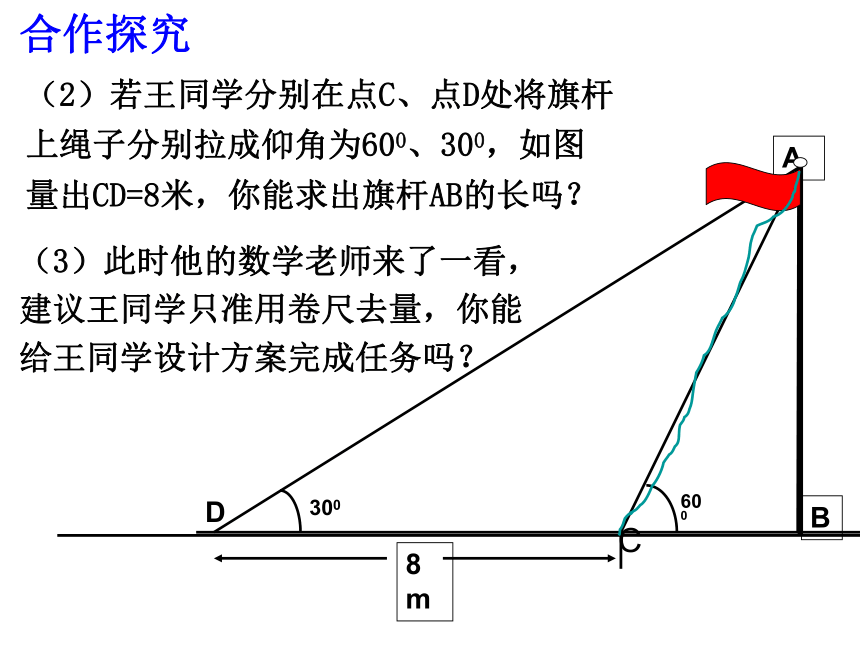
=AC×tan aA1200米BC试一试1、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30度,求飞机A到控制点B距离 . 2、如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.算出旗杆的实际高度.(精确到1米)3、某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高。(精确到0. 1米)试一试 学校操场上有一根旗杆,上面有一根升旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?合作探究(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?C合作探究(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?例2、海防哨所0发现,在它的北偏西300,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)?300450OAB500解:在Rt△AOC中,OA=500m, ∠AOC=300,∴AC=OAsin∠AOC=500sin300在Rt△BOC中, ∠BOC=450,=500×0.5=250(m)∴AC=OAcos∠AOC∴AB=AC+BC≈14000(m/h)=14(km/h)答:船的航速约为14km/h.1、某船自西向东航行,在A出测得某岛在北偏东60°的
方向上,前进8千米测得某岛在船北偏东45 °的方向
上,问(1)轮船行到何处离小岛距离最近?
(2)轮船要继续前进多少千米?做一做2、小山的高为h,为了测的小山顶上铁塔AB的高x,在平地上选择一点P, 在P点处测得B点的仰角为a, A点的仰角为B.(见表中测量目标图)题目 测量山顶铁塔的高 测量目标已知数据山高BC h=150米
仰角a a=45o
仰角B B=30o3、如图,在地面上的A点测得树顶C的仰角为30°,沿着向树的方向前进6米到达B处,测得树顶端C的仰角为45°.请画出测量示意图,求出树高CD(精确到0.1米)做一做αβ24mDACB分析:过D作DE∥BC,E问题可化归为解Rt△ABC和Rt△AED.例3、如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角a=300,测得点C 的俯角β=60°,求AB 和CD 两座建筑物的高.(结果保留根号)F已知:BC=24m, ∠α=300, ∠β=600.求:AB,CD的高.解:过D作DE∥BC,则DE⊥AB,E在Rt△ABC中,∠ACB=∠FAC=600,∴AB=BC·tan∠ACB在△ADE中,∠ADE=∠DAF=300,DE=BC=24,∴AE=DE·tan∠ADE※※※※※※※※※※※※※※※※∴CD=AB-AE1、两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45度,测得低楼的底部C点的俯角为60度,求两楼的高度。ADBC30米450600练一练2、为知道甲,乙两楼间的距离,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35012′,观测到乙楼底C的俯角为43024′.求这两楼的高度(精确到0.1m)练一练3、小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m, 两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?北ABDC15mE南练一练 小华想:若设计时要求北楼的采光,不受南楼的影响,请问楼间距BC长至少为多少米?AB?m南练一练 小华又想:如果要使北楼实验室内的同学在室内也能享受温暖阳光,已知窗台距地面1米,那么两楼应至少相距多少米?AB?m南FE练一练 1.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间
有多长?当堂训练解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中,∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响解(2):设点E、F是以A为圆心,150km为
半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。 (接上题)由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?EF 通过实践了解仰角和俯角在解直角三角形中的作用。解直角三角形的应用是数学中的应用问题,反映现实领域特征的问题情景,它包含着一定的数学概念、方法和结果。通过对实际问题的抽象提炼,分辨出解直角三角形的基本模式,用常规的代数方法解决问题。回顾整理 归纳小结船有无触礁的危险如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗?拓展练习楼梯加长了多少某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).拓展练习再见!
边长保留四个有效数字,角度精确到1′.3.两种情况:
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角1.解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.如图,在进行测量时, 从下向上看,视线与水平线的夹角叫做仰角; 从上往下看,视线与水平线的夹角叫做俯角. 知识小贴士例1 如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)在Rt△BDE中, 如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)答: 电线杆的高度约为10.4米.=9.17+1.20≈10.4(米)= AC×tana+CD ∴AB=BE+AE ∵ BE=DE×tan a
=AC×tan aA1200米BC试一试1、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30度,求飞机A到控制点B距离 . 2、如图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34°,并已知目高AD为1米.算出旗杆的实际高度.(精确到1米)3、某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高。(精确到0. 1米)试一试 学校操场上有一根旗杆,上面有一根升旗用的绳子(绳子足够长),王同学拿了一把卷尺,并且向数学老师借了一把含300的三角板去度量旗杆的高度。(1)若王同学将旗杆上绳子拉成仰角为600,如图用卷尺量得BC=4米,则旗杆AB的高多少?合作探究(2)若王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为600、300,如图量出CD=8米,你能求出旗杆AB的长吗?C合作探究(3)此时他的数学老师来了一看,建议王同学只准用卷尺去量,你能给王同学设计方案完成任务吗?例2、海防哨所0发现,在它的北偏西300,距离哨所500m的A处有一艘船向正东方向,经过3分时间后到达哨所东北方向的B处.问船从A处到B处的航速是多少km/h(精确到1km/h)?300450OAB500解:在Rt△AOC中,OA=500m, ∠AOC=300,∴AC=OAsin∠AOC=500sin300在Rt△BOC中, ∠BOC=450,=500×0.5=250(m)∴AC=OAcos∠AOC∴AB=AC+BC≈14000(m/h)=14(km/h)答:船的航速约为14km/h.1、某船自西向东航行,在A出测得某岛在北偏东60°的
方向上,前进8千米测得某岛在船北偏东45 °的方向
上,问(1)轮船行到何处离小岛距离最近?
(2)轮船要继续前进多少千米?做一做2、小山的高为h,为了测的小山顶上铁塔AB的高x,在平地上选择一点P, 在P点处测得B点的仰角为a, A点的仰角为B.(见表中测量目标图)题目 测量山顶铁塔的高 测量目标已知数据山高BC h=150米
仰角a a=45o
仰角B B=30o3、如图,在地面上的A点测得树顶C的仰角为30°,沿着向树的方向前进6米到达B处,测得树顶端C的仰角为45°.请画出测量示意图,求出树高CD(精确到0.1米)做一做αβ24mDACB分析:过D作DE∥BC,E问题可化归为解Rt△ABC和Rt△AED.例3、如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角a=300,测得点C 的俯角β=60°,求AB 和CD 两座建筑物的高.(结果保留根号)F已知:BC=24m, ∠α=300, ∠β=600.求:AB,CD的高.解:过D作DE∥BC,则DE⊥AB,E在Rt△ABC中,∠ACB=∠FAC=600,∴AB=BC·tan∠ACB在△ADE中,∠ADE=∠DAF=300,DE=BC=24,∴AE=DE·tan∠ADE※※※※※※※※※※※※※※※※∴CD=AB-AE1、两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45度,测得低楼的底部C点的俯角为60度,求两楼的高度。ADBC30米450600练一练2、为知道甲,乙两楼间的距离,测得两楼之间的距离为32.6m,从甲楼顶点A观测到乙楼顶D的俯角为35012′,观测到乙楼底C的俯角为43024′.求这两楼的高度(精确到0.1m)练一练3、小华去实验楼做实验, 两幢实验楼的高度AB=CD=20m, 两楼间的距离BC=15m,已知太阳光与水平线的夹角为30°,求南楼的影子在北楼上有多高?北ABDC15mE南练一练 小华想:若设计时要求北楼的采光,不受南楼的影响,请问楼间距BC长至少为多少米?AB?m南练一练 小华又想:如果要使北楼实验室内的同学在室内也能享受温暖阳光,已知窗台距地面1米,那么两楼应至少相距多少米?AB?m南FE练一练 1.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间
有多长?当堂训练解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中,∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响解(2):设点E、F是以A为圆心,150km为
半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。 (接上题)由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?EF 通过实践了解仰角和俯角在解直角三角形中的作用。解直角三角形的应用是数学中的应用问题,反映现实领域特征的问题情景,它包含着一定的数学概念、方法和结果。通过对实际问题的抽象提炼,分辨出解直角三角形的基本模式,用常规的代数方法解决问题。回顾整理 归纳小结船有无触礁的危险如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西550的B处,往东行驶20海里后到达该岛的南偏西250的C处.之后,货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗?拓展练习楼梯加长了多少某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).拓展练习再见!
