2.1 直线和圆的位置关系课件
图片预览






文档简介
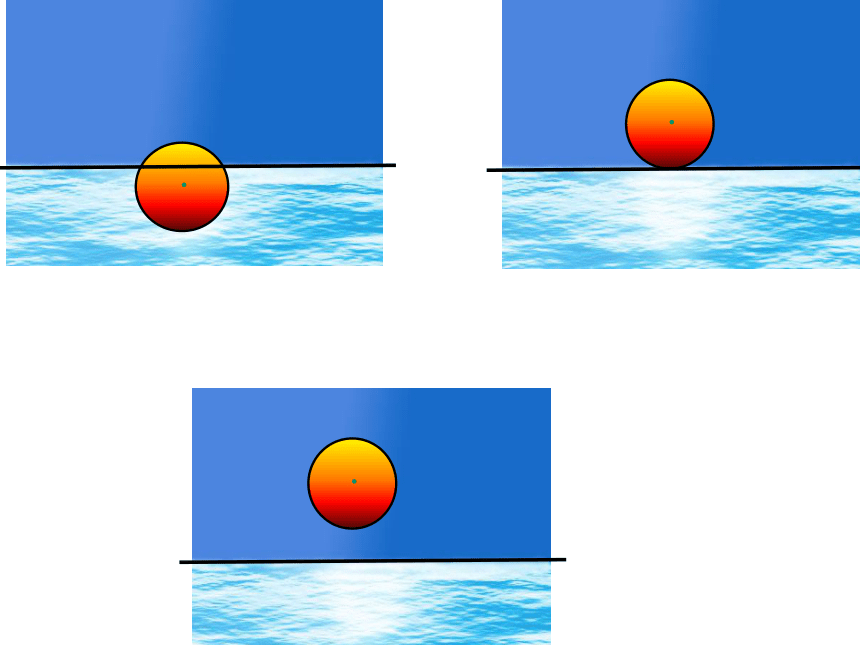
课件29张PPT。3.1(1)直线与圆的位置关系直线与圆的位置关系(3)直线和圆没有公共点时,(2)直线和圆有且只有一个公共点时,(1)直线和圆有两个公共点时,公共点叫做切点。 直线叫做圆的割线。直线和圆相交。直线和圆相切。直线叫做圆的切线直线和圆相离。说明学生举例说明生活中的三种直线与圆的位置关系(课前预习作业)
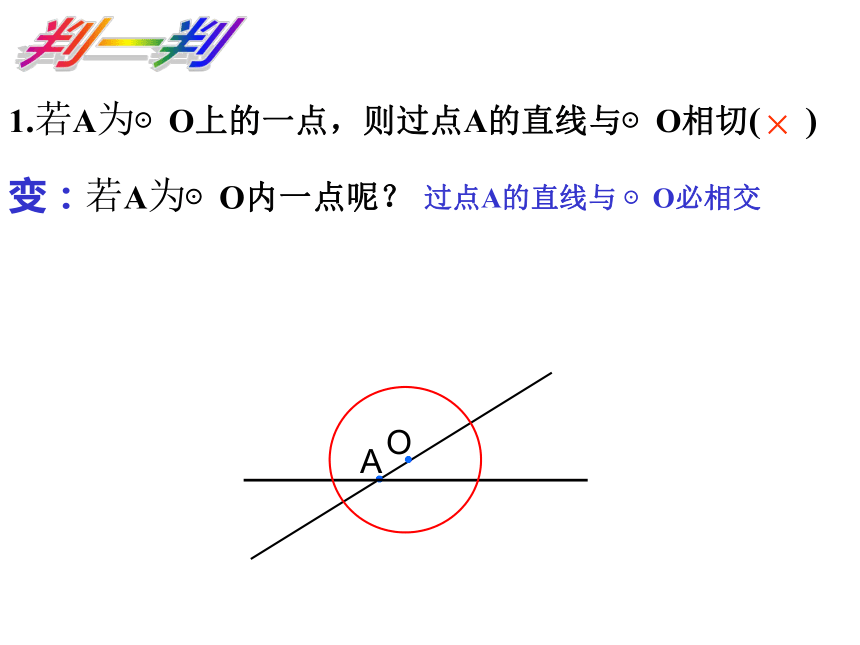
生活中找数学×.A1.若A为⊙O上的一点,则过点A的直线与⊙O相切( )判一判变:若A为⊙O内一点呢?判一判1.若A为⊙O上的一点,则过点A的直线与⊙O相切( )×过点A的直线与 ⊙O必相交 2.若A、B是⊙O外两点, 则直线AB与⊙O相离。( )×.B1.
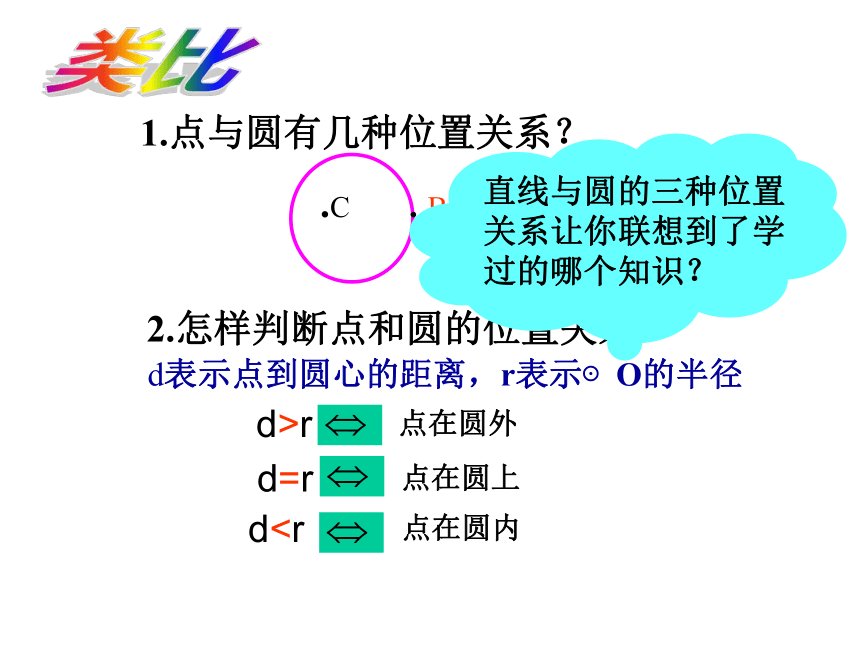
B2判一判 1.若C为⊙O上的一点,则过点C的直线与⊙O相切( ) ×变:若C为⊙O内一点呢?过点C的直线与 ⊙O必相交1.点与圆有几种位置关系?2.怎样判断点和圆的位置关系?.A . B.C类比d表示点到圆心的距离,r表示⊙O的半径d r; 直线和圆相交 直线和圆相切 直线和圆相离d r;<=>d r;直线与圆的位置关系比一比d表示圆心O到直线l的距离, r表示⊙O的半径数量关系图形位置关系课本50页作业题2画一画已知点O和直线l,求作以点O为圆心,且与直线l相切的圆。∵d=r
∴直线l与⊙O相切CD= = =2.4(cm)
AB= = =5即 圆心C到AB的距离d=2.4cm
解:过C作CD⊥AB,垂足为D,则 在△ABC中,∠C=900 , AC=3cm, BC=4cm,设⊙C的半径为r,请根据r的下列值,
判断AB与⊙C的位置关系,并说明理由。(1) r=2cm;(2) r=2.4cm(3) r=3cm 在Rt△ABC中,根据三角形的面积公式有例1(1) r = 2(2)r =2.4(3)r =3当r =2cm时,
当r =2.4cm时,
d = r,
∴☉C 与直线AB相切; 当r =3cm时,
d < r,
∴☉C 与直线AB相交。d > r,∴☉C 与直线
AB相离;在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1.当r满足________________时,⊙C与直线AB相离。2.当r满足____________ 时,⊙C与直线AB相切。3.当r满足____________时,
⊙C与直线AB相交。BCAD4530cmBC=4cm,以C为圆心,r为半径作圆。当r满足 时,
⊙C与射线AB只有一个公共点. r=2.4cm 或r>3cm
变变在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。当r满足 时,
⊙C与线段AB只有一个公共点. r=2.4cm 或3cm变变变AHBP60°30°北例2 在码头A的北偏东60°方向有一个海岛,离该岛中心P的120海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了180海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?AHBP若P为台风中心,沿西南方向以每小时30海里
的速度前行. 距台风中心120海里范围要受到影响,几小时后从A到B方向的公路受到影响。变Q直线与圆的三种位置关系.理一理数学知识:思想方法:分类讨论思想.数形结合思想.互逆思想.直线与圆的位置关系的判定方法.根据已知条件作与直线相切的圆.生活与数学.类比思想.直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r没有理一理作业1.作业本
2.课本P50组(4)(5) 希望大家如这旭日,
朝 气 蓬 勃 !1.设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为 ( )
A、d≤4 B、d<4 C、d≥4 D、d=42.设⊙P的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )
A、相交 B、相切 C、相离 D、相切或相交CD 自我检测3.已知⊙A的直径为6,点A的坐标为(-3,-4),
则⊙A与X轴的位置关系是_____,
⊙A与Y轴的位置关系是______。
相切相离同步练习与测评中均有,故改为课本作业题3和5.AO已知⊙A的直径为6,点A的坐标为(-3,-4),
则⊙A与X轴的位置关系是_____,⊙A与Y轴的
位置关系是______。BC43相离相切 如图:菱形ABCD的边长为5cm,∠B=60°
当以A为圆心的圆与BC相切时,半径是 ,
此时⊙A与CD的位置关系是 。思考题:练 习 (一)填空:1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ 。相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。零相离 在码头A的北偏东60°方向有一个海岛,离该岛中心P的15海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了18海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?解:如图,作PH⊥AB于H.则∠PAH=30°,∠PBH=60°,∴∠APB=∠PBH-∠PAB=30°∴AB=BP=18(海里)∴PH=BPsin∠PBH∴货船不会进入暗礁区=18sin60°=例2设⊙O的半径为r,圆心O到直线l的距离为d,根据下列条件判断直线l与⊙O的位置关系。(2)d=1,r= ; (3)d=2,r=2; (1)d=4,r=3;∵ d < r
∵d=r
∵d> r
说一说∴直线l与⊙O相离∴直线l与⊙O相交∴直线l与⊙O相切
生活中找数学×.A1.若A为⊙O上的一点,则过点A的直线与⊙O相切( )判一判变:若A为⊙O内一点呢?判一判1.若A为⊙O上的一点,则过点A的直线与⊙O相切( )×过点A的直线与 ⊙O必相交 2.若A、B是⊙O外两点, 则直线AB与⊙O相离。( )×.B1.
B2判一判 1.若C为⊙O上的一点,则过点C的直线与⊙O相切( ) ×变:若C为⊙O内一点呢?过点C的直线与 ⊙O必相交1.点与圆有几种位置关系?2.怎样判断点和圆的位置关系?.A . B.C类比d表示点到圆心的距离,r表示⊙O的半径d r; 直线和圆相交 直线和圆相切 直线和圆相离d r;<=>d r;直线与圆的位置关系比一比d表示圆心O到直线l的距离, r表示⊙O的半径数量关系图形位置关系课本50页作业题2画一画已知点O和直线l,求作以点O为圆心,且与直线l相切的圆。∵d=r
∴直线l与⊙O相切CD= = =2.4(cm)
AB= = =5即 圆心C到AB的距离d=2.4cm
解:过C作CD⊥AB,垂足为D,则 在△ABC中,∠C=900 , AC=3cm, BC=4cm,设⊙C的半径为r,请根据r的下列值,
判断AB与⊙C的位置关系,并说明理由。(1) r=2cm;(2) r=2.4cm(3) r=3cm 在Rt△ABC中,根据三角形的面积公式有例1(1) r = 2(2)r =2.4(3)r =3当r =2cm时,
当r =2.4cm时,
d = r,
∴☉C 与直线AB相切; 当r =3cm时,
d < r,
∴☉C 与直线AB相交。d > r,∴☉C 与直线
AB相离;在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。1.当r满足________________时,⊙C与直线AB相离。2.当r满足____________ 时,⊙C与直线AB相切。3.当r满足____________时,
⊙C与直线AB相交。BCAD4530cm
⊙C与射线AB只有一个公共点. r=2.4cm 或r>3cm
变变在Rt△ABC中,∠C=90°,AC=3cm,
BC=4cm,以C为圆心,r为半径作圆。当r满足 时,
⊙C与线段AB只有一个公共点. r=2.4cm 或3cm
的速度前行. 距台风中心120海里范围要受到影响,几小时后从A到B方向的公路受到影响。变Q直线与圆的三种位置关系.理一理数学知识:思想方法:分类讨论思想.数形结合思想.互逆思想.直线与圆的位置关系的判定方法.根据已知条件作与直线相切的圆.生活与数学.类比思想.直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r没有理一理作业1.作业本
2.课本P50组(4)(5) 希望大家如这旭日,
朝 气 蓬 勃 !1.设⊙O的半径为4,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d为 ( )
A、d≤4 B、d<4 C、d≥4 D、d=42.设⊙P的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )
A、相交 B、相切 C、相离 D、相切或相交CD 自我检测3.已知⊙A的直径为6,点A的坐标为(-3,-4),
则⊙A与X轴的位置关系是_____,
⊙A与Y轴的位置关系是______。
相切相离同步练习与测评中均有,故改为课本作业题3和5.AO已知⊙A的直径为6,点A的坐标为(-3,-4),
则⊙A与X轴的位置关系是_____,⊙A与Y轴的
位置关系是______。BC43相离相切 如图:菱形ABCD的边长为5cm,∠B=60°
当以A为圆心的圆与BC相切时,半径是 ,
此时⊙A与CD的位置关系是 。思考题:练 习 (一)填空:1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ 。相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ___ _。零相离 在码头A的北偏东60°方向有一个海岛,离该岛中心P的15海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了18海里到达B,这时岛中心P在北偏东30°方向。若货船不改变航向,问货船会不会进入暗礁区?解:如图,作PH⊥AB于H.则∠PAH=30°,∠PBH=60°,∴∠APB=∠PBH-∠PAB=30°∴AB=BP=18(海里)∴PH=BPsin∠PBH∴货船不会进入暗礁区=18sin60°=例2设⊙O的半径为r,圆心O到直线l的距离为d,根据下列条件判断直线l与⊙O的位置关系。(2)d=1,r= ; (3)d=2,r=2; (1)d=4,r=3;∵ d < r
∵d=r
∵d> r
说一说∴直线l与⊙O相离∴直线l与⊙O相交∴直线l与⊙O相切
