4.1.1多边形 课件

课件24张PPT。4.1多边形生活中的平面图形由以下各图形你抽象出什么几何图形？生活中的平面图形接着进行推测
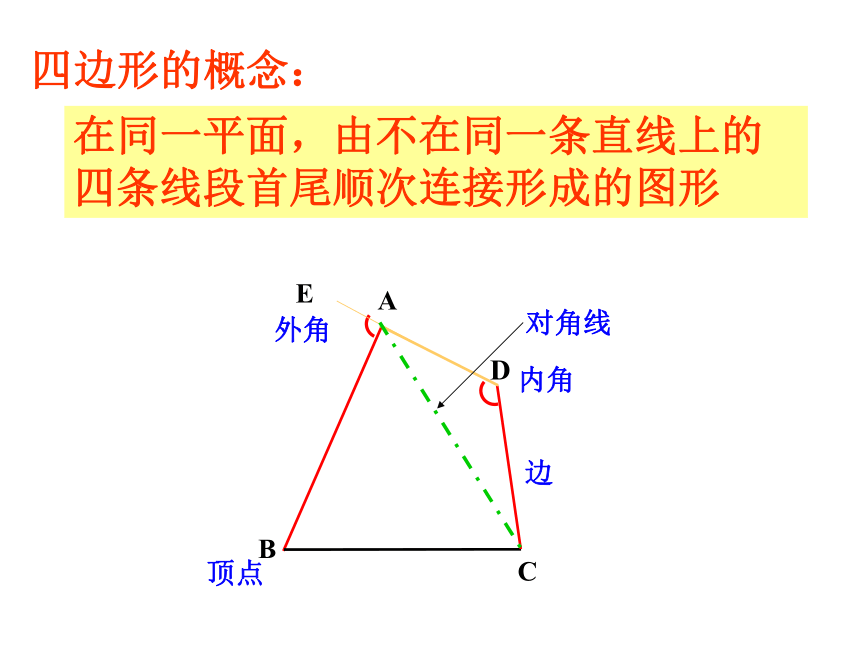
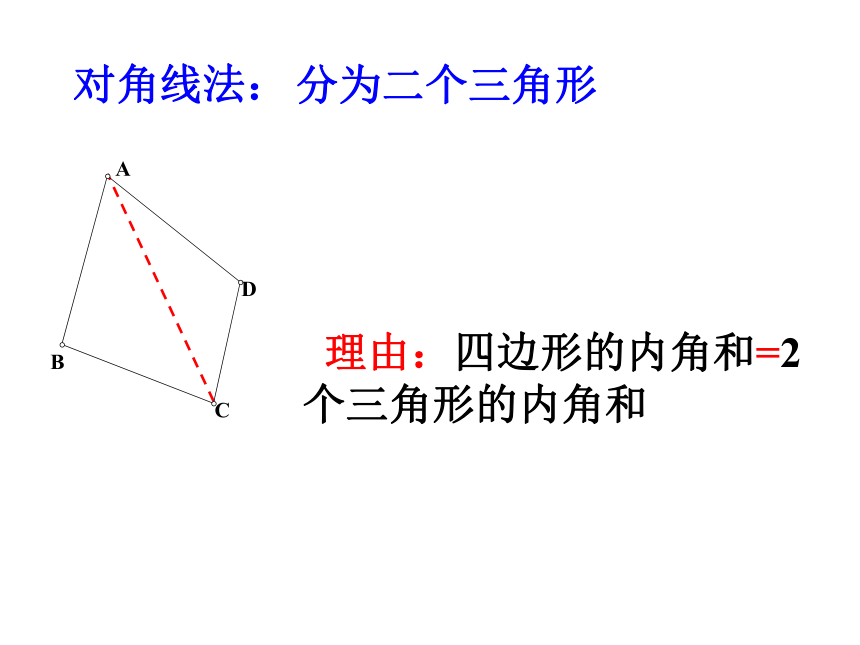
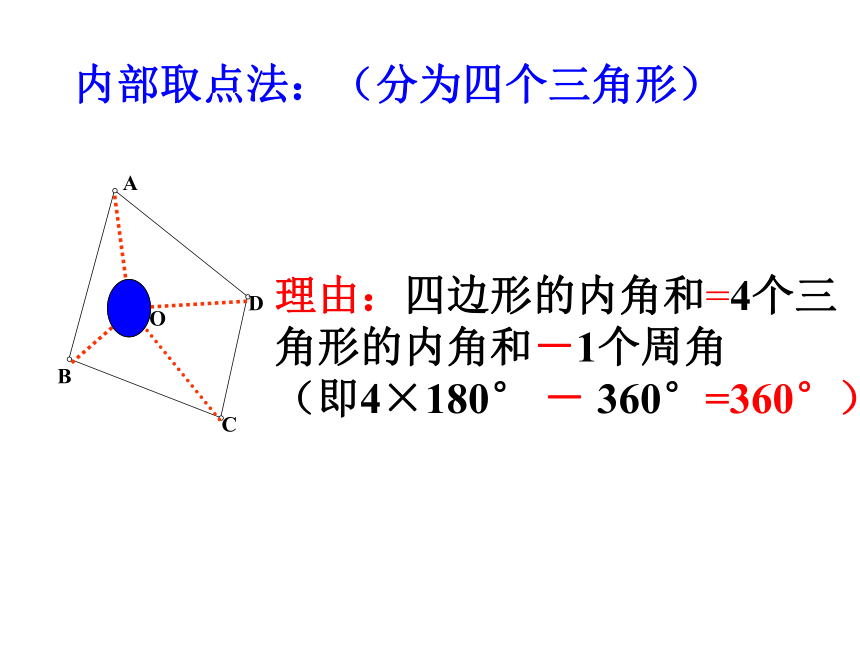
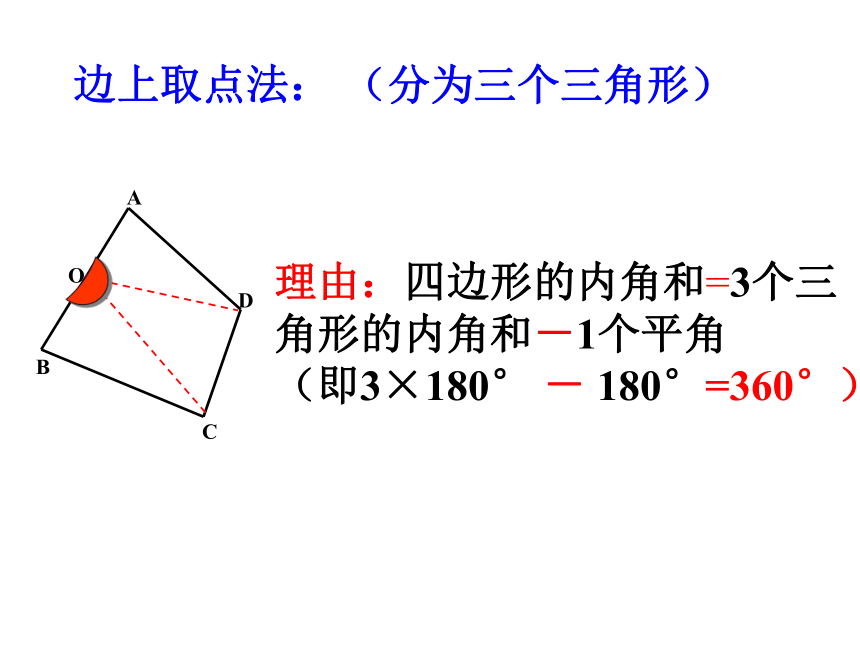
四边形的概念：在同一平面，由不在同一条直线上的四条线段首尾顺次连接形成的图形顶点内角边对角线外角四边形内角和为3600如何说明四边形的内角和为3600呢？ 理由：四边形的内角和=2个三角形的内角和对角线法：分为二个三角形 O内部取点法：（分为四个三角形）理由：四边形的内角和=4个三角形的内角和－1个周角 （即4×180° － 360°=360°）ACBD边上取点法： （分为三个三角形）理由：四边形的内角和=3个三角形的内角和－1个平角 （即3×180° － 180°=360°）问题情景： 四边形的内角和=360° 用一批大小，形状一样的四边形木板，可以拼成大面积的地板。这是利用了四边形的什么性质呢？
例1：如图，四边形风筝的四个内角∠A, ∠B, ∠C，∠D的度数之比为1：1：0.6：1 求它的四个内角的度数。解∵ ∠A+∠B+∠C+∠D=360 ° （四边形的内角和等360 °）又∵∠A，∠B，∠C，∠D的度数之比为1：1：0.6：1设∠A=x度，则x+x+0.6x+x=360,
解得x=100.∴∠A=∠B=∠D=100 °，
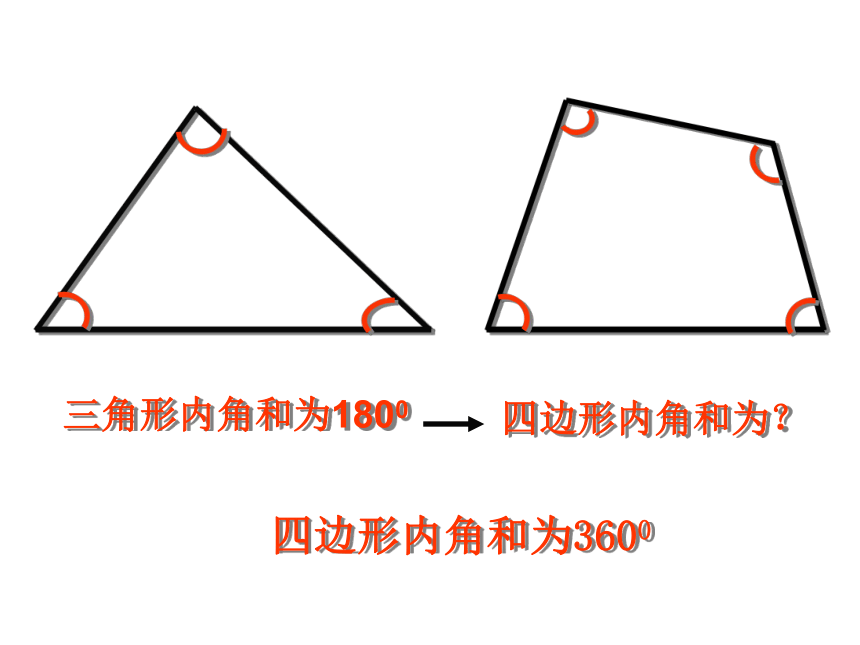
∠C=100 °×0.6=60 °四边形的外角和为多少呢?即∠1+∠2+∠3+∠4 = ?∠1+∠2+∠3+∠4 = 3600 小明有每天坚持跑步的好习惯，右图就是小明清晨沿一个四边形广场逆时针方向跑步的效果图. 请你观察并思考如下问题:(1) 小明每从一条街道转到下一条街道时，身体转过的角是哪些角？在图中标出它们.
ABCD1234(2)他每跑完一圈，身体转过的角度之和是多少？ 即∠ 1+∠2+∠3+∠4＝360 °你能说出你的理由吗？练习四边形9036°72°108°144° 在同一平面内，由不在同一条直线上的一些线段首尾顺次相接所组成的图形。三角形六边形四边形八边形多边形……..连结多边形不相邻的两个顶点的线段，叫做多边形的对角线。五边形31×180o =180o45n2×180o =360o3×180o =540o(n-2)×180o n边形合作学习多边形的内角和3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和 例1 已知一个多边形，它的内角和等于外角和的2倍，求这个多边形的边数.解： 设多边形的边数为n因为它的内角和等于(n-2)?180°
而它的外角和等于360o所以解得答：这个多边形的边数为6例2 一个多边形每个内角都等于144o，求它的边数. 例3 一个多边形每个外角都等于30o，求它的边数.课内练习:（2）已知一个多边形的内角和为900o ，则这个边形是______边形7（1）十边形的内角和为______，外角和为_____1440o360o（3）已知一个多边形的每一个外角都是72o，求这个边形的边数为______5（4）在五边形ABCDE中，若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______80o例4:一个六边形,已知AB//DE,BC//EF,CD//AF,求∠A+∠C+∠E的度数。ACDBEDCBAFEDCBA顶点与其不相邻顶点的连线，叫做多边形对角线2(n-3)(n-3)问3：n边形的对角线总条数有多少条？为什么？n边形的边数从一个顶点所画对角线的条数n边形对角线的条数345…nn-3521200所以n边形对角线的条数为……F小结：1、四边形的概念和有关性质
2、多边形的内角、外角、对角线的概念
3、 n边形对角线的条数为4、 n边形内角和为5、任意多边形的外角和为360°