第1章第03讲证明(3类题型)(含解析)2023-2024学年八年级数学上册浙教版
文档属性
| 名称 | 第1章第03讲证明(3类题型)(含解析)2023-2024学年八年级数学上册浙教版 |  | |
| 格式 | docx | ||
| 文件大小 | 597.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-16 22:19:36 | ||
图片预览




文档简介
第03讲 证明(3类题型)
课程标准 学习目标
1.了解证明的概念和过程; 1、了解证明的含义。2、体验、理解证明的必要性和推理过程中要步步有据。 3、了解证明的表达格式,会按规定格式证明简单命题。 4、通过证明步骤中由命题画出图形,写出已知、求证的过程,继续训练学生由几何语句正确画出几何图形的能力。
知识点01:证明
证明:从命题的条件出发,根据已知的定义、基本事实、定理(包括推论)、一步一步推得结论成立的推理过程。
证明几何命题的格式:(1)按题意画出图形(2)分清命题的条件和结论,结合图形,在已知中写出条件,在求证中写出结论(3)在证明中写出推理过程。
在解决几何问题时,有时需要添加辅助线。添辅助线的过程要写入证明中,辅助线通常画成虚线。
【即学即练1】
(2022春·浙江宁波·八年级校考期中)
1.用反证法证明,“在中,对边是a、b.若,则.”第一步应假设( )
A. B. C. D.
【即学即练2】
(2022秋·八年级课时练习)
2.某超市(商场)失窃,大量的商品在夜间被罪犯用汽车运走.三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在甲、乙、丙三人之外;(2)丙作案时总得有甲作从犯;(3)乙不会开车.在此案中,能肯定的作案对象是( )
A.嫌疑犯乙 B.嫌疑犯丙 C.嫌疑犯甲 D.嫌疑犯甲和丙
题型01 以代数为背景的推理与论证
(2023春·七年级课前预习)
3.卡塔尔世界杯已经结束,阿根廷捧得大力神杯!我们知道,世界杯小组赛分成8个小组,每小组4个队,小组内进行单循环赛(两支球队间只比赛一场),已知胜一场积3分,平一场积1分,负一场积0分,小组赛结束后,积分前两名(相同积分比较净胜球)进入16强.
下表是世界杯E组积分表:
排名 球队 积分
1 日本 6
2 西班牙 4
3 德国 4
4 哥斯达黎加 ?
如果本小组比赛中只有一场战平,根据此表,可以推断哥斯达黎加的积分是( )
A.0 B.1 C.2 D.3
(2023·浙江·八年级假期作业)
4.描金又称泥金画漆,是一种传统工艺美术技艺.起源于战国时期,在漆器表面,用金色描绘花纹的装饰方法,常以黑漆作底,也有少数以朱漆为底.描金工作分为两道工序,第一道工序是上漆,第二道工序是描绘花纹.现甲、乙两位工匠要完成,,三件原料的描金工作,每件原料先由甲上漆,再由乙描绘花纹.每道工序所需的时间单位:小时如下:
原料 时间 工序 原料 原料 原料
上漆
描绘花纹
则完成这三件原料的描金工作最少需要 小时.
(2022秋·八年级课时练习)
5.当时,代数式的值分别是7,5,5,7,11,它们都是质数,那么,命题“对于自然数n,代数式的值都是质数”是真命题吗?
题型02 逻辑推理与论证
(2023春·江苏无锡·七年级无锡市天一实验学校校考阶段练习)
6.甲和乙玩一个猜数游戏,规则如下:已知五张纸牌上分别写有2、3、4、5、6五个数字,现甲、乙两人分别从中各自随机取一张,然后根据自己手中的数推测谁手上的数更大,甲看了看自己手中的数,想了想说:我不知道谁手中的数更大;乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大。假设甲、乙所作出的推理都是正确的,那么乙手中的数是( )
A.5 B.4 C.3 D.不能确定
(2023春·七年级课前预习)
7.现有一个三位数密码锁,已知以下3个条件,可以推断正确的密码是 .
①只有一个号码正确且位置正确
②只有两个号码正确且位置都不正确
③三个号码都不正确
(2022秋·八年级课时练习)
8.推理能力都很强的甲、乙、丙站成一列,丙可以看见甲、乙,乙可以看见甲但看不见丙,甲看不见乙、丙.现有5顶帽子,3顶白色,2顶黑色.老师分别给每人戴上一顶帽子(在各自不知道的情况下).老师先问丙是否知道头上的帽子颜色,丙回答说不知道;老师再问乙是否知道头上的帽子颜色,乙也回答说不知道;老师最后问甲是否知道头上的帽子颜色,甲回答说知道.请你说出甲戴了什么颜色的帽子,并写出推理过程.
题型03 证明
(2021·河北·统考中考真题)
9.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,是的外角.
求证:.
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
(2023春·七年级课时练习)
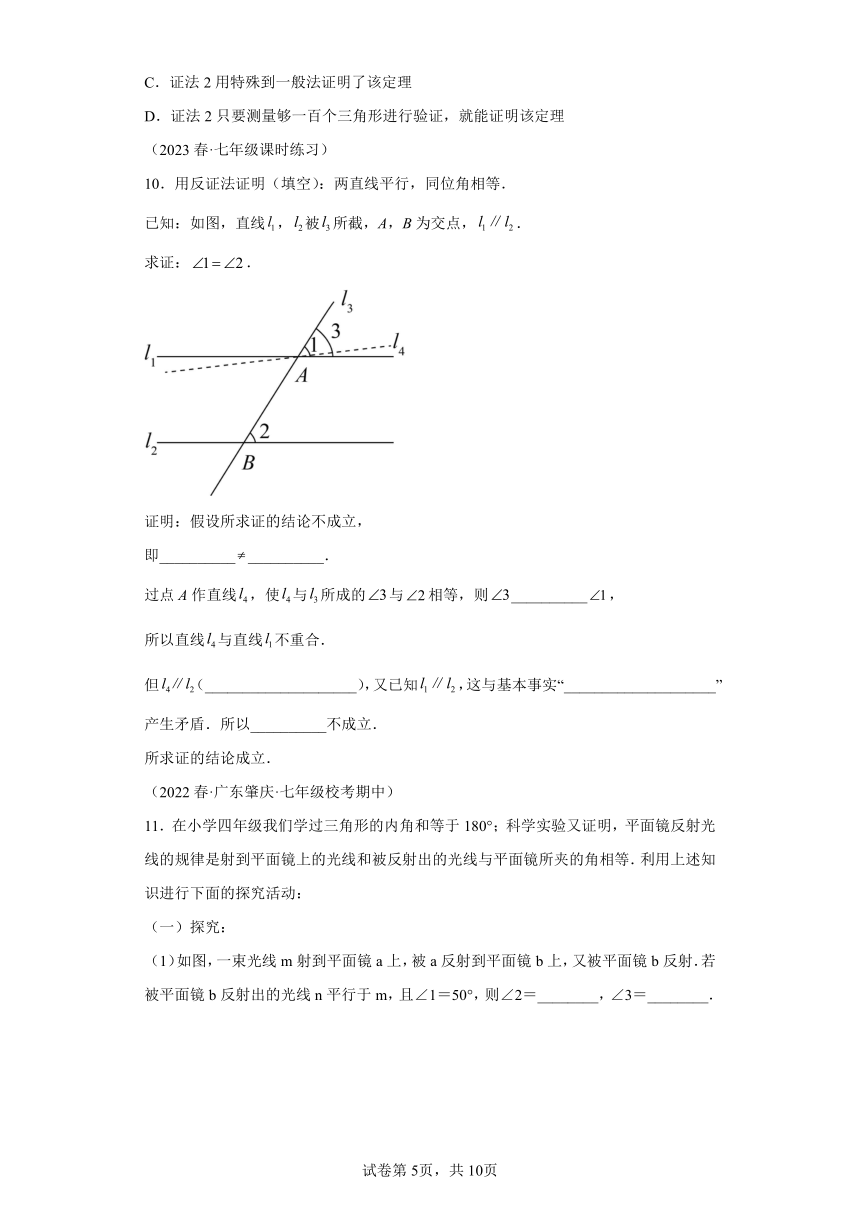
10.用反证法证明(填空):两直线平行,同位角相等.
已知:如图,直线,被所截,A,B为交点,.
求证:.
证明:假设所求证的结论不成立,
即____________________.
过点A作直线,使与所成的与相等,则__________,
所以直线与直线不重合.
但(____________________),又已知,这与基本事实“____________________”产生矛盾.所以__________不成立.
所求证的结论成立.
(2022春·广东肇庆·七年级校考期中)
11.在小学四年级我们学过三角形的内角和等于180°;科学实验又证明,平面镜反射光线的规律是射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.利用上述知识进行下面的探究活动:
(一)探究:
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被平面镜b反射.若被平面镜b反射出的光线n平行于m,且∠1=50°,则∠2=________,∠3=________.
(2)在(1)中,若∠1=40°,则∠3=________;若∠1=55°,则∠3=________.
(二)猜想:
(3)由(1)(2),请你猜想:当∠3=________时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的.
(三)(4)证明:请证明你的上述猜想.
A夯实基础
(2023春·七年级课时练习)
12.在第届全国中学生物理竞赛决赛中,华师一物理竞赛团队有位同学获金牌,并全部进入国家集训队.五位同学猜谁是第一名,说:是,说:是,说:是,说:说错了,说:不是我.教练说:你们中只有一人说对了,那么第一名是( )
A.B B.C C.D D.E
(2022秋·湖北省直辖县级单位·八年级校联考期中)
13.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
(2018春·八年级课时练习)
14.三角形的三条角平分线相交于一点,并且这一点到 相等
15.用反证法证明“已知,.求证:”.第一步应先假设 .
(2023春·全国·七年级专题练习)
16.如图,一组直线a,b,c,d是否都互相平行?
(2022秋·八年级课时练习)
17.已知:如图,在中,是的平分线,,.求证:.
B能力提升
(2023春·七年级课前预习)
18.卡塔尔世界杯已经结束,阿根廷捧得大力神杯!我们知道,世界杯小组赛分成8个小组,每小组4个队,小组内进行单循环赛(两支球队间只比赛一场),已知胜一场积3分,平一场积1分,负一场积0分,小组赛结束后,积分前两名(相同积分比较净胜球)进入16强.
下表是世界杯E组积分表:
排名 球队 积分
1 日本 6
2 西班牙 4
3 德国 4
4 哥斯达黎加 ?
如果本小组比赛中只有一场战平,根据此表,可以推断哥斯达黎加的积分是( )
A.0 B.1 C.2 D.3
(2023·浙江·八年级假期作业)
19.小王、小陈、小张当中有一人做了一件好事,另两人也都知道是谁做了这件事.老师在了解情况时,他们三人分别说了下面几句话:
小陈:“我没做这件事.”“小张也没做这件事.”
小王:“我没做这件事.”“小陈也没做这件事.”
小张:“我没做这件事.”“我也不知道谁做了这件事.”
已知他们每人都说了一句假话,一句真话,做好事的人是( )
A.小王 B.小陈 C.小张 D.不能确定
(2023·浙江·八年级假期作业)
20.描金又称泥金画漆,是一种传统工艺美术技艺.起源于战国时期,在漆器表面,用金色描绘花纹的装饰方法,常以黑漆作底,也有少数以朱漆为底.描金工作分为两道工序,第一道工序是上漆,第二道工序是描绘花纹.现甲、乙两位工匠要完成,,三件原料的描金工作,每件原料先由甲上漆,再由乙描绘花纹.每道工序所需的时间单位:小时如下:
原料 时间 工序 原料 原料 原料
上漆
描绘花纹
则完成这三件原料的描金工作最少需要 小时.
(2023春·七年级课时练习)
21.用反证法证明(填空):两直线平行,同位角相等.
已知:如图,直线,被所截,A,B为交点,.
求证:.
证明:假设所求证的结论不成立,
即____________________.
过点A作直线,使与所成的与相等,则__________,
所以直线与直线不重合.
但(____________________),又已知,这与基本事实“____________________”产生矛盾.所以__________不成立.
所求证的结论成立.
(2023春·全国·七年级专题练习)
22.已知:如图,,求证:.
(2023·浙江·八年级假期作业)
23.已知:如图,的两条高线、相交于点O.求证:.
证明:∵、是的两条高线( ),
( )
( ),
.
.
C综合素养
(2023春·江苏无锡·七年级无锡市天一实验学校校考阶段练习)
24.甲和乙玩一个猜数游戏,规则如下:已知五张纸牌上分别写有2、3、4、5、6五个数字,现甲、乙两人分别从中各自随机取一张,然后根据自己手中的数推测谁手上的数更大,甲看了看自己手中的数,想了想说:我不知道谁手中的数更大;乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大。假设甲、乙所作出的推理都是正确的,那么乙手中的数是( )
A.5 B.4 C.3 D.不能确定
(2023春·七年级课时练习)
25.甲、乙、丙3人用擂台赛形式进行训练,每局2人进行单打比赛,另1人当裁判,每一局的输方当下一局的裁判,由原来的裁判向胜者挑战.半天训练结束时,发现甲共打了12局,乙共打了21局,而丙共当裁判8局.那么,整个比赛的第10局的输方( )
A.必是甲 B.必是乙 C.必是丙 D.不能确定
(2023春·江苏·七年级专题练习)
26.盒子里有甲、乙、丙三种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗乙粒子;不同种类的两颗粒子发生碰撞,会变成第三种粒子,例如一颗甲粒子和一颗乙粒子发生碰撞则变成一颗丙粒子,现有甲粒子6颗,乙粒子4颗,丙粒子5颗,如果经过各种两两碰撞后,只剩下1颗粒子,给出下列结论:①最后一颗粒子可能是甲粒子;②最后一颗粒子一定不是乙粒子;③最后一颗粒子可能是丙粒子.其中正确结论的序号是: .
(2023春·七年级课前预习)
27.现有一个三位数密码锁,已知以下3个条件,可以推断正确的密码是 .
①只有一个号码正确且位置正确
②只有两个号码正确且位置都不正确
③三个号码都不正确
(2023秋·浙江杭州·八年级校考开学考试)
28.证明命题“三角形不共顶点的三个外角的和等于”是真命题.
(2020秋·江苏泰州·八年级校考阶段练习)
29.如何将用数轴上的点表示?关键是画出长为的线段.方法1:因为,所以我们可以通过画两条直角边分别为1、2的直角三角形来解决,我们把此法称为“和法”;方法2:因为,所以我们可以通过画直角边为2,斜边为3的直角三角形来解决,我们把此法称为“差法”.
(1)用“差法”将用数轴上的点表示(注:需用尺规作图,保留作图痕迹,不写画法)
(2)对于正整数n,猜想当n是什么数时,我们都能通过“差法”,将用数轴上的点表示,并证明你的猜想.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据反证法的步骤,直接选择即可.
【详解】解:根据反证法的步骤,得
第一步应假设不成立,即.
故选:D.
【点睛】本题考查了反证法,熟知反证法的步骤是关键.
2.C
【分析】根据大量的商品在夜间被罪犯用汽车运走和条件(3)可知,案犯显然不是乙;根据条件(1)可知作案对象一定在甲、丙中间,或两人都是嫌犯.由(2)得,若丙作案,那么甲必作案,但是没有证据能够直接证明丙一定作案,所以嫌疑犯必是甲.
【详解】解:由于“大量的商品在夜间被罪犯用汽车运走”,根据条件(3)可知:乙肯定不是主犯;
根据(1)可知:嫌疑犯必在甲和丙之间;
由(2)知:若丙作案,则甲必作案;
由于没有直接证明丙作案的证据,因此根据(1)(2)可以确定的是甲一定是嫌疑犯.
故选C.
【点睛】本题考查了推理与证明,解决问题的关键是读懂题意,能够运用排除法分析解决此类问题.
3.D
【分析】根据题意可得小组内每个队进行3场比赛,一共进行了场,再由表格可得日本队,西班牙队,德国队的胜负情况,即可求解.
【详解】解:根据题意得:小组内每个队进行3场比赛,一共进行了场,
∵日本队得6分,
∴日本队胜2场,负1场,
∵西班牙队得4分,
∴西班牙队胜1场,平1场,负1场,
∵德国队得4分,
∴德国队胜1场,平1场,负1场,
∴哥斯达黎加队可以是胜1场,负2场,也可以是平2场,负1场,
∵本小组比赛中只有一场战平,那就是西班牙队和德国队战平,
∴斯达黎加队胜1场,负2场,
∴哥斯达黎加的积分是3分.
故选:D
【点睛】本题主要考查了逻辑推理,明确题意,准确得到日本队,西班牙队,德国队的胜负情况是解题的关键.
4.
【分析】根据分析,甲按、、的顺序,乙中途不会出现停顿进行解答即可.
【详解】甲按、、的顺序,完成这三件原料的描金工作最少需要(小时),
故答案为:.
【点睛】此题考查推理与论证,关键是得出工作顺序.
5.不是真命题
【分析】对于命题“对于自然数n,代数式的值都是质数”是真命题,可以举出反例进行判断.
【详解】解:当时,代数式的值分别是7,5,5,7,11,
当时,代数式=,17是质数;
而对于所有自然数,式子的值不一定是质数
如当时,,25不是质数.
故当时,代数式的值都是质数,对于所有的自然数n,代数式的值不一定是质数.
故命题“对于自然数n,代数式的值都是质数”不是真命题
【点睛】此题考查了代数式求值,命题的真假.此题难度适中,注意掌握举反例法的应用是解此题的关键.
6.B
【分析】先分析甲手中的数,根据甲不知道谁手中的数更大,推出甲手中的数不可能为2和6,再根据乙也不知道谁手中的数更大,即可推出乙手中的数不可能为3和5,即可得出答案
【详解】五张纸牌上分别写有2、3、4、5、6五个数字,
∵甲看了看自己手中的数,想了想说:我不知道谁手中的数更大,
∴甲手中的数可能为3,4,5,
∵乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大.
∴乙手中的数不可能是3,5,只能是4.
故选:B.
【点睛】本题考查逻辑推理,考查简单的合情推理,根据题目意思分析判断是解题的关键.
7.520
【分析】根据题意分析分析推理即可,由①结合③可以确定第三位数字为0,由②,③可以确定前两个数为5,2,据此分析即可.
【详解】根据①,③可知正确的号码是0,位置是第三位,由②,③可知正确的号码是5,2,位置分别为第一位和第二位,所以正确的密码是520.
【点睛】本题考查了逻辑推理,根据题意结合所给信息推导出各位数字是解题的关键.
8.甲戴的是白帽子,理由见解析
【分析】如果甲、乙都戴黑帽子,丙马上知道自己戴的是白帽子,如果甲戴黑帽子,甲、乙中至少有一个人戴白帽子,则乙马上知道自己戴的是白帽子.
【详解】解:甲戴的是白帽子.理由如下:
因为丙说不知道,说明甲、乙中至少有一个人戴白帽子(如果甲、乙都戴黑帽子,丙马上知道自己戴的是白帽子).
因为乙也说不知道,说明甲戴的是白帽子(如果甲戴黑帽子,甲、乙中至少有一个人戴白帽子,则乙马上知道自己戴的是白帽子).
【点睛】本题主要考查了论证与推理的一些基础知识,能够找出题中的内在联系,从而求解.
9.B
【分析】根据三角形的内角和定理与平角的定义可判断A与B,利用理论与实践相结合可判断C与D.
【详解】解:A. 证法1给出的证明过程是完整正确的,不需要分情况讨论,故A不符合题意;
B. 证法1给出的证明过程是完整正确的,不需要分情况讨论,故选项B符合题意;
C. 证法2用量角器度量两个内角和外角,只能验证该定理的正确性,用特殊到一般法证明了该定理缺少理论证明过程,故选项C不符合题意;
D. 证法2只要测量够一百个三角形进行验证,验证的正确性更高,就能证明该定理还需用理论证明,故选项D不符合题意.
故选择:
【点睛】本题考查三角形外角的证明问题,命题的正确性需要严密推理证明,三角形外角分三种情形,锐角、直角、和钝角,证明中应分类才严谨.
10.、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,
【分析】假设命题的结论不成立,从这个假设出发,经过推理论证,得出矛盾即可.
【详解】解:假设所求证的结论不成立,
即.
过点A作直线,使与所成的与相等,则,
所以直线与直线不重合.
但(同位角相等两直线平行),又已知,这与基本事实“过直线外一点有且只有一条直线与已知直线平行”产生矛盾.所以不成立.
所求证的结论成立,
故答案为:、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,.
【点睛】本题考查了反证法,解题的关键是记住反证法的步骤:否定结论,得出矛盾,肯定结论.
11.(1)100°;90°;(2)90°;90°;(3)90°;(4)见解析
【分析】(1)如图,根据入射角等于反射角可求得∠1=∠4,∠5=∠6,进而求得∠7=80°,再由m∥n求出∠2=100°,进而求得∠5=40°,根据三角形内角和为180°即可求得答案;
(2)结合(1)中过程可得∠3=90°;
(3)根据(1)(2)结论,猜想当∠3=90°时,m∥n;
(4)由∠3=90°证得∠2与∠7互补即可.
【详解】(一)(1)如图,∵入射角等于反射角,
∴∠1=∠4,∠5=∠6,
∴∠7=180°-∠1-∠4=80°,
∵m∥n,
∴∠7+∠2=180°,
∴∠2=180°-∠7=100°,
∴∠5=∠6=(180°-100°)÷2=40°
根据三角形的内角和为180°,得:
∠3=180°-∠4-∠5=90°,
故答案为:100°,90°;
(2)由(1)可知∠3的度数都是90°,
故答案为:90°,90°;
(二)(3)由(1)(2)可猜想:当∠3=90°时,m∥n,
故答案为:90°;
(三)(4)证明:当∠3=90°时,.m∥n.
理由如下:
∵ ∠ 3=90°,
∴ ∠ 4+∠ 5=180° 90°=90°,
∵∠ 1=∠ 4,∠ 5=∠ 6,
∴ ∠ 1+∠ 4+∠ 5+∠ 6=2×90°=180°,
∴ ∠ 7+∠ 2=180° (∠ 1+∠ 4)+180° (∠ 5+∠ 6)=180°,
∴ m∥n.
【点睛】本题考查平行线的判定与性质,还涉及入射角等于反射角、平角定义、三角形的内角和定理等知识,解答的关键是认真审题,掌握入射角等于反射角这一重要性质,利用平行线的性质得出∠3=90°,进而利用特殊到一般,归纳与类比、猜想与证明的解题方法解决问题.
12.D
【分析】教练说:你们中只有一人说对了,根据,相互矛盾,由此即可求解.
【详解】解:说:是,说:说错了,教练说:你们中只有一人说对了,
∴和的说法只能一真一假,不能同真,也不能同假;
∴和,说得都是假话,
∴只有说对了,
故选:.
【点睛】本题主要考查命题的逻辑推理,理解题目中教练,和的说法进行推导是解题的关键.
13.B
【分析】利用角平分线性质定理可得,角平分线上的点到角两边的距离相等,通过等量代换即可得.
【详解】解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
【点睛】掌握角平分线的性质为本题的关键.
14.三边的距离
【详解】三角形三条角平分线的交点到三角形三条边的距离相等.
故答案为三边的距离.
15.
【分析】用反证法证明问题的关键是清楚结论的反面是什么,写出与条件相反的假设即可
【详解】解: “已知,.求证:”.第一步应先假设.
故答案为:.
【点睛】本题考查的是反证法的应用,解题的关键是要懂得反证法的意义及步骤.在假设结论不成立时,要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
16.直线a,b,c,d都互相平行,理由见解析
【分析】根据平行公理证明即可.
【详解】解:直线a,b,c,d都互相平行,理由如下:
∵,
∴.
【点睛】本题主要考查了平行公理,熟知平行于同一直线的两条直线平行是解题的关键.
17.证明见解析
【分析】先根据三角形外角的性质求出,再根据角平分线的定义求出的度数,最后根据三角形内角和定理求出的度数即可证明结论.
【详解】证明:∵,,
∴,
∵是的平分线,
∴,
∴,
∴.
【点睛】本题主要考查了三角形外角的性质,角平分线的定义,三角形内角和定理,利用三角形外角的性质求出是解题的关键.
18.D
【分析】根据题意可得小组内每个队进行3场比赛,一共进行了场,再由表格可得日本队,西班牙队,德国队的胜负情况,即可求解.
【详解】解:根据题意得:小组内每个队进行3场比赛,一共进行了场,
∵日本队得6分,
∴日本队胜2场,负1场,
∵西班牙队得4分,
∴西班牙队胜1场,平1场,负1场,
∵德国队得4分,
∴德国队胜1场,平1场,负1场,
∴哥斯达黎加队可以是胜1场,负2场,也可以是平2场,负1场,
∵本小组比赛中只有一场战平,那就是西班牙队和德国队战平,
∴斯达黎加队胜1场,负2场,
∴哥斯达黎加的积分是3分.
故选:D
【点睛】本题主要考查了逻辑推理,明确题意,准确得到日本队,西班牙队,德国队的胜负情况是解题的关键.
19.B
【分析】根据题意对小陈说的两句话来假设真假,再对后面两人说的话逐一分析,得出矛盾的即假设不成立,不矛盾的则符合条件.
【详解】解:1、假设小陈说“我没做这件事”是真话,则“小张也没做这件事”是假话,从这里可以得出做好事的就是小张;假设小王说“我没做这件事”是真话,则“小陈也没做这件事”是假话,从这里可以得出做好事的就是小陈,与小陈的假设矛盾;
2、假设小陈说“我没做这件事”是假话,则“小张也没做这件事”是真话,从这里可以得出做好事的就是小陈;假设小王说“我没做这件事”是真话,则“小陈也没做这件事”是假话,从这里可以得出做好事的就是小陈;符合;假设小张说“我没做这件事”是真话,则“也不知道谁做了这件事”是假话,符合;
∴做好事的是小陈,
故选B.
【点睛】逻辑推理问题,用到的数学知识不多,主要依靠对已知条件的分析,寻找适当的突破口,常用枚举、归谬等方法.
20.
【分析】根据分析,甲按、、的顺序,乙中途不会出现停顿进行解答即可.
【详解】甲按、、的顺序,完成这三件原料的描金工作最少需要(小时),
故答案为:.
【点睛】此题考查推理与论证,关键是得出工作顺序.
21.、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,
【分析】假设命题的结论不成立,从这个假设出发,经过推理论证,得出矛盾即可.
【详解】解:假设所求证的结论不成立,
即.
过点A作直线,使与所成的与相等,则,
所以直线与直线不重合.
但(同位角相等两直线平行),又已知,这与基本事实“过直线外一点有且只有一条直线与已知直线平行”产生矛盾.所以不成立.
所求证的结论成立,
故答案为:、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,.
【点睛】本题考查了反证法,解题的关键是记住反证法的步骤:否定结论,得出矛盾,肯定结论.
22.见解析
【分析】根据平行线的性质定理,进而得出,则,即可得出.
【详解】证明:过点C作,
∴,
∵,
∴,
∴,
∴.
【点睛】此题主要考查了平行线的判定与性质,熟练掌握相关的定理是解题关键,解题时注意:同旁内角互补,两直线平行.
23.已知;三角形高的定义;三角形外角的性质
【分析】根据三角形高的定义得到,根据三角形外角的性质得到,则.
【详解】证明:∵、是的两条高线(已知),
∴(三角形高的定义)
∵(三角形外角的性质),
∴.
∴,
故答案为:已知;三角形高的定义;三角形外角的性质.
【点睛】本题主要考查了三角形高的定义,三角形外角的性质,熟知三角形的一个外角等于与其不相邻的两个内角之和是解题的关键.
24.B
【分析】先分析甲手中的数,根据甲不知道谁手中的数更大,推出甲手中的数不可能为2和6,再根据乙也不知道谁手中的数更大,即可推出乙手中的数不可能为3和5,即可得出答案
【详解】五张纸牌上分别写有2、3、4、5、6五个数字,
∵甲看了看自己手中的数,想了想说:我不知道谁手中的数更大,
∴甲手中的数可能为3,4,5,
∵乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大.
∴乙手中的数不可能是3,5,只能是4.
故选:B.
【点睛】本题考查逻辑推理,考查简单的合情推理,根据题目意思分析判断是解题的关键.
25.A
【分析】根据丙共当裁判8局,因此,甲乙打了8局;甲共打了12局,因此,丙甲共打了4局,利用乙共打了21局,因此,乙丙打了13局.因此,共打了25局,那么,甲当裁判13局,乙当裁判4局,丙当裁判8局,由于实行擂台赛形式,因此,每局都必须换裁判;即,某人不可能连续做裁判.因此,甲做裁判的局次只能是:1、3、5、…、23、25;由于第11局只能是甲做裁判,显然,第10局的输方,只能是甲,据此即可判定.
【详解】解:根据题意,知丙共当裁判8局,所以甲乙之间共有8局比赛,
又甲共打了12局,乙共打了21局,所以甲和丙打了4局,乙和丙打了13局,
三个人之间总共打了(8+4+13)=25局,
考查甲,总共打了12局,当了13次裁判,所以他输了12次.
所以当n是偶数时,第n局比赛的输方为甲,从而整个比赛的第10局的输方必是甲.
故选:A.
【点睛】此题主要考查了推理论证,要首先能够判断出比赛的总场数以及三人各自当裁判的次数,然后根据甲当的裁判次数和总的场数进行分析求解.
26.①②③.
【分析】根据规律将问题分三类分别分析,先剩下1颗丙,其它产生乙种粒子与原来4颗乙粒子共有9颗中8颗乙粒子两两碰撞最后剩一颗乙与丙碰撞产生丙即可解决.
【详解】解:∵相同种类的两颗粒子发生碰撞,则变成一颗乙粒子;不同种类的两颗粒子发生碰撞,会变成第三种粒子,甲粒子与乙粒子碰撞产生丙粒子,甲粒子与丙粒子碰撞产生乙粒子,乙粒子与丙粒子碰撞产生甲粒子,
6颗甲粒子两两碰撞产生3颗乙粒子,
5颗丙粒子中4颗丙粒子两两碰撞产生2颗乙粒子,
一共有9颗乙粒子,8个两两碰撞产生4个乙粒子加剩下一个共5个乙粒子,5个乙粒子中4个再两两碰撞产生2个,与剩下1个一共有3个乙粒子,其中两个相碰撞产生1个乙粒子与剩下的一个共有2个乙粒子,其中分两种情况,
当剩下两个乙粒子碰撞中一个与丙相碰撞产生一个甲,与乙先碰撞,最后产生丙粒子,
当剩下两颗乙粒子相碰撞产生一颗乙粒子与丙粒子相碰撞最后产生甲粒子,
①最后一颗粒子可能是甲粒子正确;
②最后一颗粒子一定不是乙粒子正确;
③最后一颗粒子可能是丙粒子正确.
正确的序号是①②③.
故答案为:①②③.
【点睛】本题考查了分类思想,逻辑推理,分析问题解决问题的能力,读懂题意是解题的关键.
27.520
【分析】根据题意分析分析推理即可,由①结合③可以确定第三位数字为0,由②,③可以确定前两个数为5,2,据此分析即可.
【详解】根据①,③可知正确的号码是0,位置是第三位,由②,③可知正确的号码是5,2,位置分别为第一位和第二位,所以正确的密码是520.
【点睛】本题考查了逻辑推理,根据题意结合所给信息推导出各位数字是解题的关键.
28.见解析
【分析】利用三角形外角的性质得到,再由三角形内角和定理得到,即可证明.
【详解】已知:如图,是的三个外角;
求证:.
证明:∵,
∴,
∵,
∴,
∴命题“三角形不共顶点的三个外角的和等于”是真命题.
【点睛】本题主要考查了证明命题,三角形内角和定理和三角形外角的性质,熟知三角形外角的性质是解题的关键.
29.(1)见解析;(2)当n为奇数时,均可通过“差法”,将用数轴上的点表示
【分析】(1)过原点作射线OA,再以原点O为圆心,用圆规截取一个单位长度为半径画弧交OA为点B,以B为圆心截取两个单位长度为半径画弧交x轴于点C,此时线段OC=;
(2)当n为奇数时,均可通过“差法”,将 用数轴上的点表示;将n为奇数代入证明即可.
【详解】(1)过原点作射线OA,再以原点O为圆心,用圆规截取一个单位长度为半径画弧交OA为点B,以B为圆心截取两个单位长度为半径画弧交x轴于点C,此时线段OC=;
(2)当n为奇数时,均可通过“差法”,将 用数轴上的点表示;
当n为奇数时:
①
②
③
④
……
∴观察可知:差法的前一个数比它后面的数大1,
∴设(x=y+1),
∴
∴ 当n为奇数时,均可通过“差法”,将 用数轴上的点表示.
【点睛】本题考查了作图,并由图观察规律进行证明,正确掌握知识点是解题的关键.
答案第1页,共2页
答案第1页,共2页
课程标准 学习目标
1.了解证明的概念和过程; 1、了解证明的含义。2、体验、理解证明的必要性和推理过程中要步步有据。 3、了解证明的表达格式,会按规定格式证明简单命题。 4、通过证明步骤中由命题画出图形,写出已知、求证的过程,继续训练学生由几何语句正确画出几何图形的能力。
知识点01:证明
证明:从命题的条件出发,根据已知的定义、基本事实、定理(包括推论)、一步一步推得结论成立的推理过程。
证明几何命题的格式:(1)按题意画出图形(2)分清命题的条件和结论,结合图形,在已知中写出条件,在求证中写出结论(3)在证明中写出推理过程。
在解决几何问题时,有时需要添加辅助线。添辅助线的过程要写入证明中,辅助线通常画成虚线。
【即学即练1】
(2022春·浙江宁波·八年级校考期中)
1.用反证法证明,“在中,对边是a、b.若,则.”第一步应假设( )
A. B. C. D.
【即学即练2】
(2022秋·八年级课时练习)
2.某超市(商场)失窃,大量的商品在夜间被罪犯用汽车运走.三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:(1)罪犯不在甲、乙、丙三人之外;(2)丙作案时总得有甲作从犯;(3)乙不会开车.在此案中,能肯定的作案对象是( )
A.嫌疑犯乙 B.嫌疑犯丙 C.嫌疑犯甲 D.嫌疑犯甲和丙
题型01 以代数为背景的推理与论证
(2023春·七年级课前预习)
3.卡塔尔世界杯已经结束,阿根廷捧得大力神杯!我们知道,世界杯小组赛分成8个小组,每小组4个队,小组内进行单循环赛(两支球队间只比赛一场),已知胜一场积3分,平一场积1分,负一场积0分,小组赛结束后,积分前两名(相同积分比较净胜球)进入16强.
下表是世界杯E组积分表:
排名 球队 积分
1 日本 6
2 西班牙 4
3 德国 4
4 哥斯达黎加 ?
如果本小组比赛中只有一场战平,根据此表,可以推断哥斯达黎加的积分是( )
A.0 B.1 C.2 D.3
(2023·浙江·八年级假期作业)
4.描金又称泥金画漆,是一种传统工艺美术技艺.起源于战国时期,在漆器表面,用金色描绘花纹的装饰方法,常以黑漆作底,也有少数以朱漆为底.描金工作分为两道工序,第一道工序是上漆,第二道工序是描绘花纹.现甲、乙两位工匠要完成,,三件原料的描金工作,每件原料先由甲上漆,再由乙描绘花纹.每道工序所需的时间单位:小时如下:
原料 时间 工序 原料 原料 原料
上漆
描绘花纹
则完成这三件原料的描金工作最少需要 小时.
(2022秋·八年级课时练习)
5.当时,代数式的值分别是7,5,5,7,11,它们都是质数,那么,命题“对于自然数n,代数式的值都是质数”是真命题吗?
题型02 逻辑推理与论证
(2023春·江苏无锡·七年级无锡市天一实验学校校考阶段练习)
6.甲和乙玩一个猜数游戏,规则如下:已知五张纸牌上分别写有2、3、4、5、6五个数字,现甲、乙两人分别从中各自随机取一张,然后根据自己手中的数推测谁手上的数更大,甲看了看自己手中的数,想了想说:我不知道谁手中的数更大;乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大。假设甲、乙所作出的推理都是正确的,那么乙手中的数是( )
A.5 B.4 C.3 D.不能确定
(2023春·七年级课前预习)
7.现有一个三位数密码锁,已知以下3个条件,可以推断正确的密码是 .
①只有一个号码正确且位置正确
②只有两个号码正确且位置都不正确
③三个号码都不正确
(2022秋·八年级课时练习)
8.推理能力都很强的甲、乙、丙站成一列,丙可以看见甲、乙,乙可以看见甲但看不见丙,甲看不见乙、丙.现有5顶帽子,3顶白色,2顶黑色.老师分别给每人戴上一顶帽子(在各自不知道的情况下).老师先问丙是否知道头上的帽子颜色,丙回答说不知道;老师再问乙是否知道头上的帽子颜色,乙也回答说不知道;老师最后问甲是否知道头上的帽子颜色,甲回答说知道.请你说出甲戴了什么颜色的帽子,并写出推理过程.
题型03 证明
(2021·河北·统考中考真题)
9.定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,是的外角.
求证:.
下列说法正确的是( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
(2023春·七年级课时练习)
10.用反证法证明(填空):两直线平行,同位角相等.
已知:如图,直线,被所截,A,B为交点,.
求证:.
证明:假设所求证的结论不成立,
即____________________.
过点A作直线,使与所成的与相等,则__________,
所以直线与直线不重合.
但(____________________),又已知,这与基本事实“____________________”产生矛盾.所以__________不成立.
所求证的结论成立.
(2022春·广东肇庆·七年级校考期中)
11.在小学四年级我们学过三角形的内角和等于180°;科学实验又证明,平面镜反射光线的规律是射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.利用上述知识进行下面的探究活动:
(一)探究:
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被平面镜b反射.若被平面镜b反射出的光线n平行于m,且∠1=50°,则∠2=________,∠3=________.
(2)在(1)中,若∠1=40°,则∠3=________;若∠1=55°,则∠3=________.
(二)猜想:
(3)由(1)(2),请你猜想:当∠3=________时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的.
(三)(4)证明:请证明你的上述猜想.
A夯实基础
(2023春·七年级课时练习)
12.在第届全国中学生物理竞赛决赛中,华师一物理竞赛团队有位同学获金牌,并全部进入国家集训队.五位同学猜谁是第一名,说:是,说:是,说:是,说:说错了,说:不是我.教练说:你们中只有一人说对了,那么第一名是( )
A.B B.C C.D D.E
(2022秋·湖北省直辖县级单位·八年级校联考期中)
13.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
(2018春·八年级课时练习)
14.三角形的三条角平分线相交于一点,并且这一点到 相等
15.用反证法证明“已知,.求证:”.第一步应先假设 .
(2023春·全国·七年级专题练习)
16.如图,一组直线a,b,c,d是否都互相平行?
(2022秋·八年级课时练习)
17.已知:如图,在中,是的平分线,,.求证:.
B能力提升
(2023春·七年级课前预习)
18.卡塔尔世界杯已经结束,阿根廷捧得大力神杯!我们知道,世界杯小组赛分成8个小组,每小组4个队,小组内进行单循环赛(两支球队间只比赛一场),已知胜一场积3分,平一场积1分,负一场积0分,小组赛结束后,积分前两名(相同积分比较净胜球)进入16强.
下表是世界杯E组积分表:
排名 球队 积分
1 日本 6
2 西班牙 4
3 德国 4
4 哥斯达黎加 ?
如果本小组比赛中只有一场战平,根据此表,可以推断哥斯达黎加的积分是( )
A.0 B.1 C.2 D.3
(2023·浙江·八年级假期作业)
19.小王、小陈、小张当中有一人做了一件好事,另两人也都知道是谁做了这件事.老师在了解情况时,他们三人分别说了下面几句话:
小陈:“我没做这件事.”“小张也没做这件事.”
小王:“我没做这件事.”“小陈也没做这件事.”
小张:“我没做这件事.”“我也不知道谁做了这件事.”
已知他们每人都说了一句假话,一句真话,做好事的人是( )
A.小王 B.小陈 C.小张 D.不能确定
(2023·浙江·八年级假期作业)
20.描金又称泥金画漆,是一种传统工艺美术技艺.起源于战国时期,在漆器表面,用金色描绘花纹的装饰方法,常以黑漆作底,也有少数以朱漆为底.描金工作分为两道工序,第一道工序是上漆,第二道工序是描绘花纹.现甲、乙两位工匠要完成,,三件原料的描金工作,每件原料先由甲上漆,再由乙描绘花纹.每道工序所需的时间单位:小时如下:
原料 时间 工序 原料 原料 原料
上漆
描绘花纹
则完成这三件原料的描金工作最少需要 小时.
(2023春·七年级课时练习)
21.用反证法证明(填空):两直线平行,同位角相等.
已知:如图,直线,被所截,A,B为交点,.
求证:.
证明:假设所求证的结论不成立,
即____________________.
过点A作直线,使与所成的与相等,则__________,
所以直线与直线不重合.
但(____________________),又已知,这与基本事实“____________________”产生矛盾.所以__________不成立.
所求证的结论成立.
(2023春·全国·七年级专题练习)
22.已知:如图,,求证:.
(2023·浙江·八年级假期作业)
23.已知:如图,的两条高线、相交于点O.求证:.
证明:∵、是的两条高线( ),
( )
( ),
.
.
C综合素养
(2023春·江苏无锡·七年级无锡市天一实验学校校考阶段练习)
24.甲和乙玩一个猜数游戏,规则如下:已知五张纸牌上分别写有2、3、4、5、6五个数字,现甲、乙两人分别从中各自随机取一张,然后根据自己手中的数推测谁手上的数更大,甲看了看自己手中的数,想了想说:我不知道谁手中的数更大;乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大。假设甲、乙所作出的推理都是正确的,那么乙手中的数是( )
A.5 B.4 C.3 D.不能确定
(2023春·七年级课时练习)
25.甲、乙、丙3人用擂台赛形式进行训练,每局2人进行单打比赛,另1人当裁判,每一局的输方当下一局的裁判,由原来的裁判向胜者挑战.半天训练结束时,发现甲共打了12局,乙共打了21局,而丙共当裁判8局.那么,整个比赛的第10局的输方( )
A.必是甲 B.必是乙 C.必是丙 D.不能确定
(2023春·江苏·七年级专题练习)
26.盒子里有甲、乙、丙三种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗乙粒子;不同种类的两颗粒子发生碰撞,会变成第三种粒子,例如一颗甲粒子和一颗乙粒子发生碰撞则变成一颗丙粒子,现有甲粒子6颗,乙粒子4颗,丙粒子5颗,如果经过各种两两碰撞后,只剩下1颗粒子,给出下列结论:①最后一颗粒子可能是甲粒子;②最后一颗粒子一定不是乙粒子;③最后一颗粒子可能是丙粒子.其中正确结论的序号是: .
(2023春·七年级课前预习)
27.现有一个三位数密码锁,已知以下3个条件,可以推断正确的密码是 .
①只有一个号码正确且位置正确
②只有两个号码正确且位置都不正确
③三个号码都不正确
(2023秋·浙江杭州·八年级校考开学考试)
28.证明命题“三角形不共顶点的三个外角的和等于”是真命题.
(2020秋·江苏泰州·八年级校考阶段练习)
29.如何将用数轴上的点表示?关键是画出长为的线段.方法1:因为,所以我们可以通过画两条直角边分别为1、2的直角三角形来解决,我们把此法称为“和法”;方法2:因为,所以我们可以通过画直角边为2,斜边为3的直角三角形来解决,我们把此法称为“差法”.
(1)用“差法”将用数轴上的点表示(注:需用尺规作图,保留作图痕迹,不写画法)
(2)对于正整数n,猜想当n是什么数时,我们都能通过“差法”,将用数轴上的点表示,并证明你的猜想.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】根据反证法的步骤,直接选择即可.
【详解】解:根据反证法的步骤,得
第一步应假设不成立,即.
故选:D.
【点睛】本题考查了反证法,熟知反证法的步骤是关键.
2.C
【分析】根据大量的商品在夜间被罪犯用汽车运走和条件(3)可知,案犯显然不是乙;根据条件(1)可知作案对象一定在甲、丙中间,或两人都是嫌犯.由(2)得,若丙作案,那么甲必作案,但是没有证据能够直接证明丙一定作案,所以嫌疑犯必是甲.
【详解】解:由于“大量的商品在夜间被罪犯用汽车运走”,根据条件(3)可知:乙肯定不是主犯;
根据(1)可知:嫌疑犯必在甲和丙之间;
由(2)知:若丙作案,则甲必作案;
由于没有直接证明丙作案的证据,因此根据(1)(2)可以确定的是甲一定是嫌疑犯.
故选C.
【点睛】本题考查了推理与证明,解决问题的关键是读懂题意,能够运用排除法分析解决此类问题.
3.D
【分析】根据题意可得小组内每个队进行3场比赛,一共进行了场,再由表格可得日本队,西班牙队,德国队的胜负情况,即可求解.
【详解】解:根据题意得:小组内每个队进行3场比赛,一共进行了场,
∵日本队得6分,
∴日本队胜2场,负1场,
∵西班牙队得4分,
∴西班牙队胜1场,平1场,负1场,
∵德国队得4分,
∴德国队胜1场,平1场,负1场,
∴哥斯达黎加队可以是胜1场,负2场,也可以是平2场,负1场,
∵本小组比赛中只有一场战平,那就是西班牙队和德国队战平,
∴斯达黎加队胜1场,负2场,
∴哥斯达黎加的积分是3分.
故选:D
【点睛】本题主要考查了逻辑推理,明确题意,准确得到日本队,西班牙队,德国队的胜负情况是解题的关键.
4.
【分析】根据分析,甲按、、的顺序,乙中途不会出现停顿进行解答即可.
【详解】甲按、、的顺序,完成这三件原料的描金工作最少需要(小时),
故答案为:.
【点睛】此题考查推理与论证,关键是得出工作顺序.
5.不是真命题
【分析】对于命题“对于自然数n,代数式的值都是质数”是真命题,可以举出反例进行判断.
【详解】解:当时,代数式的值分别是7,5,5,7,11,
当时,代数式=,17是质数;
而对于所有自然数,式子的值不一定是质数
如当时,,25不是质数.
故当时,代数式的值都是质数,对于所有的自然数n,代数式的值不一定是质数.
故命题“对于自然数n,代数式的值都是质数”不是真命题
【点睛】此题考查了代数式求值,命题的真假.此题难度适中,注意掌握举反例法的应用是解此题的关键.
6.B
【分析】先分析甲手中的数,根据甲不知道谁手中的数更大,推出甲手中的数不可能为2和6,再根据乙也不知道谁手中的数更大,即可推出乙手中的数不可能为3和5,即可得出答案
【详解】五张纸牌上分别写有2、3、4、5、6五个数字,
∵甲看了看自己手中的数,想了想说:我不知道谁手中的数更大,
∴甲手中的数可能为3,4,5,
∵乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大.
∴乙手中的数不可能是3,5,只能是4.
故选:B.
【点睛】本题考查逻辑推理,考查简单的合情推理,根据题目意思分析判断是解题的关键.
7.520
【分析】根据题意分析分析推理即可,由①结合③可以确定第三位数字为0,由②,③可以确定前两个数为5,2,据此分析即可.
【详解】根据①,③可知正确的号码是0,位置是第三位,由②,③可知正确的号码是5,2,位置分别为第一位和第二位,所以正确的密码是520.
【点睛】本题考查了逻辑推理,根据题意结合所给信息推导出各位数字是解题的关键.
8.甲戴的是白帽子,理由见解析
【分析】如果甲、乙都戴黑帽子,丙马上知道自己戴的是白帽子,如果甲戴黑帽子,甲、乙中至少有一个人戴白帽子,则乙马上知道自己戴的是白帽子.
【详解】解:甲戴的是白帽子.理由如下:
因为丙说不知道,说明甲、乙中至少有一个人戴白帽子(如果甲、乙都戴黑帽子,丙马上知道自己戴的是白帽子).
因为乙也说不知道,说明甲戴的是白帽子(如果甲戴黑帽子,甲、乙中至少有一个人戴白帽子,则乙马上知道自己戴的是白帽子).
【点睛】本题主要考查了论证与推理的一些基础知识,能够找出题中的内在联系,从而求解.
9.B
【分析】根据三角形的内角和定理与平角的定义可判断A与B,利用理论与实践相结合可判断C与D.
【详解】解:A. 证法1给出的证明过程是完整正确的,不需要分情况讨论,故A不符合题意;
B. 证法1给出的证明过程是完整正确的,不需要分情况讨论,故选项B符合题意;
C. 证法2用量角器度量两个内角和外角,只能验证该定理的正确性,用特殊到一般法证明了该定理缺少理论证明过程,故选项C不符合题意;
D. 证法2只要测量够一百个三角形进行验证,验证的正确性更高,就能证明该定理还需用理论证明,故选项D不符合题意.
故选择:
【点睛】本题考查三角形外角的证明问题,命题的正确性需要严密推理证明,三角形外角分三种情形,锐角、直角、和钝角,证明中应分类才严谨.
10.、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,
【分析】假设命题的结论不成立,从这个假设出发,经过推理论证,得出矛盾即可.
【详解】解:假设所求证的结论不成立,
即.
过点A作直线,使与所成的与相等,则,
所以直线与直线不重合.
但(同位角相等两直线平行),又已知,这与基本事实“过直线外一点有且只有一条直线与已知直线平行”产生矛盾.所以不成立.
所求证的结论成立,
故答案为:、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,.
【点睛】本题考查了反证法,解题的关键是记住反证法的步骤:否定结论,得出矛盾,肯定结论.
11.(1)100°;90°;(2)90°;90°;(3)90°;(4)见解析
【分析】(1)如图,根据入射角等于反射角可求得∠1=∠4,∠5=∠6,进而求得∠7=80°,再由m∥n求出∠2=100°,进而求得∠5=40°,根据三角形内角和为180°即可求得答案;
(2)结合(1)中过程可得∠3=90°;
(3)根据(1)(2)结论,猜想当∠3=90°时,m∥n;
(4)由∠3=90°证得∠2与∠7互补即可.
【详解】(一)(1)如图,∵入射角等于反射角,
∴∠1=∠4,∠5=∠6,
∴∠7=180°-∠1-∠4=80°,
∵m∥n,
∴∠7+∠2=180°,
∴∠2=180°-∠7=100°,
∴∠5=∠6=(180°-100°)÷2=40°
根据三角形的内角和为180°,得:
∠3=180°-∠4-∠5=90°,
故答案为:100°,90°;
(2)由(1)可知∠3的度数都是90°,
故答案为:90°,90°;
(二)(3)由(1)(2)可猜想:当∠3=90°时,m∥n,
故答案为:90°;
(三)(4)证明:当∠3=90°时,.m∥n.
理由如下:
∵ ∠ 3=90°,
∴ ∠ 4+∠ 5=180° 90°=90°,
∵∠ 1=∠ 4,∠ 5=∠ 6,
∴ ∠ 1+∠ 4+∠ 5+∠ 6=2×90°=180°,
∴ ∠ 7+∠ 2=180° (∠ 1+∠ 4)+180° (∠ 5+∠ 6)=180°,
∴ m∥n.
【点睛】本题考查平行线的判定与性质,还涉及入射角等于反射角、平角定义、三角形的内角和定理等知识,解答的关键是认真审题,掌握入射角等于反射角这一重要性质,利用平行线的性质得出∠3=90°,进而利用特殊到一般,归纳与类比、猜想与证明的解题方法解决问题.
12.D
【分析】教练说:你们中只有一人说对了,根据,相互矛盾,由此即可求解.
【详解】解:说:是,说:说错了,教练说:你们中只有一人说对了,
∴和的说法只能一真一假,不能同真,也不能同假;
∴和,说得都是假话,
∴只有说对了,
故选:.
【点睛】本题主要考查命题的逻辑推理,理解题目中教练,和的说法进行推导是解题的关键.
13.B
【分析】利用角平分线性质定理可得,角平分线上的点到角两边的距离相等,通过等量代换即可得.
【详解】解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
【点睛】掌握角平分线的性质为本题的关键.
14.三边的距离
【详解】三角形三条角平分线的交点到三角形三条边的距离相等.
故答案为三边的距离.
15.
【分析】用反证法证明问题的关键是清楚结论的反面是什么,写出与条件相反的假设即可
【详解】解: “已知,.求证:”.第一步应先假设.
故答案为:.
【点睛】本题考查的是反证法的应用,解题的关键是要懂得反证法的意义及步骤.在假设结论不成立时,要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
16.直线a,b,c,d都互相平行,理由见解析
【分析】根据平行公理证明即可.
【详解】解:直线a,b,c,d都互相平行,理由如下:
∵,
∴.
【点睛】本题主要考查了平行公理,熟知平行于同一直线的两条直线平行是解题的关键.
17.证明见解析
【分析】先根据三角形外角的性质求出,再根据角平分线的定义求出的度数,最后根据三角形内角和定理求出的度数即可证明结论.
【详解】证明:∵,,
∴,
∵是的平分线,
∴,
∴,
∴.
【点睛】本题主要考查了三角形外角的性质,角平分线的定义,三角形内角和定理,利用三角形外角的性质求出是解题的关键.
18.D
【分析】根据题意可得小组内每个队进行3场比赛,一共进行了场,再由表格可得日本队,西班牙队,德国队的胜负情况,即可求解.
【详解】解:根据题意得:小组内每个队进行3场比赛,一共进行了场,
∵日本队得6分,
∴日本队胜2场,负1场,
∵西班牙队得4分,
∴西班牙队胜1场,平1场,负1场,
∵德国队得4分,
∴德国队胜1场,平1场,负1场,
∴哥斯达黎加队可以是胜1场,负2场,也可以是平2场,负1场,
∵本小组比赛中只有一场战平,那就是西班牙队和德国队战平,
∴斯达黎加队胜1场,负2场,
∴哥斯达黎加的积分是3分.
故选:D
【点睛】本题主要考查了逻辑推理,明确题意,准确得到日本队,西班牙队,德国队的胜负情况是解题的关键.
19.B
【分析】根据题意对小陈说的两句话来假设真假,再对后面两人说的话逐一分析,得出矛盾的即假设不成立,不矛盾的则符合条件.
【详解】解:1、假设小陈说“我没做这件事”是真话,则“小张也没做这件事”是假话,从这里可以得出做好事的就是小张;假设小王说“我没做这件事”是真话,则“小陈也没做这件事”是假话,从这里可以得出做好事的就是小陈,与小陈的假设矛盾;
2、假设小陈说“我没做这件事”是假话,则“小张也没做这件事”是真话,从这里可以得出做好事的就是小陈;假设小王说“我没做这件事”是真话,则“小陈也没做这件事”是假话,从这里可以得出做好事的就是小陈;符合;假设小张说“我没做这件事”是真话,则“也不知道谁做了这件事”是假话,符合;
∴做好事的是小陈,
故选B.
【点睛】逻辑推理问题,用到的数学知识不多,主要依靠对已知条件的分析,寻找适当的突破口,常用枚举、归谬等方法.
20.
【分析】根据分析,甲按、、的顺序,乙中途不会出现停顿进行解答即可.
【详解】甲按、、的顺序,完成这三件原料的描金工作最少需要(小时),
故答案为:.
【点睛】此题考查推理与论证,关键是得出工作顺序.
21.、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,
【分析】假设命题的结论不成立,从这个假设出发,经过推理论证,得出矛盾即可.
【详解】解:假设所求证的结论不成立,
即.
过点A作直线,使与所成的与相等,则,
所以直线与直线不重合.
但(同位角相等两直线平行),又已知,这与基本事实“过直线外一点有且只有一条直线与已知直线平行”产生矛盾.所以不成立.
所求证的结论成立,
故答案为:、,,同位角相等,两直线平行,过直线外一点有且只有一条直线与已知直线平行,.
【点睛】本题考查了反证法,解题的关键是记住反证法的步骤:否定结论,得出矛盾,肯定结论.
22.见解析
【分析】根据平行线的性质定理,进而得出,则,即可得出.
【详解】证明:过点C作,
∴,
∵,
∴,
∴,
∴.
【点睛】此题主要考查了平行线的判定与性质,熟练掌握相关的定理是解题关键,解题时注意:同旁内角互补,两直线平行.
23.已知;三角形高的定义;三角形外角的性质
【分析】根据三角形高的定义得到,根据三角形外角的性质得到,则.
【详解】证明:∵、是的两条高线(已知),
∴(三角形高的定义)
∵(三角形外角的性质),
∴.
∴,
故答案为:已知;三角形高的定义;三角形外角的性质.
【点睛】本题主要考查了三角形高的定义,三角形外角的性质,熟知三角形的一个外角等于与其不相邻的两个内角之和是解题的关键.
24.B
【分析】先分析甲手中的数,根据甲不知道谁手中的数更大,推出甲手中的数不可能为2和6,再根据乙也不知道谁手中的数更大,即可推出乙手中的数不可能为3和5,即可得出答案
【详解】五张纸牌上分别写有2、3、4、5、6五个数字,
∵甲看了看自己手中的数,想了想说:我不知道谁手中的数更大,
∴甲手中的数可能为3,4,5,
∵乙听了甲的判断后,思索了一下说:我也不知道谁手中的数更大.
∴乙手中的数不可能是3,5,只能是4.
故选:B.
【点睛】本题考查逻辑推理,考查简单的合情推理,根据题目意思分析判断是解题的关键.
25.A
【分析】根据丙共当裁判8局,因此,甲乙打了8局;甲共打了12局,因此,丙甲共打了4局,利用乙共打了21局,因此,乙丙打了13局.因此,共打了25局,那么,甲当裁判13局,乙当裁判4局,丙当裁判8局,由于实行擂台赛形式,因此,每局都必须换裁判;即,某人不可能连续做裁判.因此,甲做裁判的局次只能是:1、3、5、…、23、25;由于第11局只能是甲做裁判,显然,第10局的输方,只能是甲,据此即可判定.
【详解】解:根据题意,知丙共当裁判8局,所以甲乙之间共有8局比赛,
又甲共打了12局,乙共打了21局,所以甲和丙打了4局,乙和丙打了13局,
三个人之间总共打了(8+4+13)=25局,
考查甲,总共打了12局,当了13次裁判,所以他输了12次.
所以当n是偶数时,第n局比赛的输方为甲,从而整个比赛的第10局的输方必是甲.
故选:A.
【点睛】此题主要考查了推理论证,要首先能够判断出比赛的总场数以及三人各自当裁判的次数,然后根据甲当的裁判次数和总的场数进行分析求解.
26.①②③.
【分析】根据规律将问题分三类分别分析,先剩下1颗丙,其它产生乙种粒子与原来4颗乙粒子共有9颗中8颗乙粒子两两碰撞最后剩一颗乙与丙碰撞产生丙即可解决.
【详解】解:∵相同种类的两颗粒子发生碰撞,则变成一颗乙粒子;不同种类的两颗粒子发生碰撞,会变成第三种粒子,甲粒子与乙粒子碰撞产生丙粒子,甲粒子与丙粒子碰撞产生乙粒子,乙粒子与丙粒子碰撞产生甲粒子,
6颗甲粒子两两碰撞产生3颗乙粒子,
5颗丙粒子中4颗丙粒子两两碰撞产生2颗乙粒子,
一共有9颗乙粒子,8个两两碰撞产生4个乙粒子加剩下一个共5个乙粒子,5个乙粒子中4个再两两碰撞产生2个,与剩下1个一共有3个乙粒子,其中两个相碰撞产生1个乙粒子与剩下的一个共有2个乙粒子,其中分两种情况,
当剩下两个乙粒子碰撞中一个与丙相碰撞产生一个甲,与乙先碰撞,最后产生丙粒子,
当剩下两颗乙粒子相碰撞产生一颗乙粒子与丙粒子相碰撞最后产生甲粒子,
①最后一颗粒子可能是甲粒子正确;
②最后一颗粒子一定不是乙粒子正确;
③最后一颗粒子可能是丙粒子正确.
正确的序号是①②③.
故答案为:①②③.
【点睛】本题考查了分类思想,逻辑推理,分析问题解决问题的能力,读懂题意是解题的关键.
27.520
【分析】根据题意分析分析推理即可,由①结合③可以确定第三位数字为0,由②,③可以确定前两个数为5,2,据此分析即可.
【详解】根据①,③可知正确的号码是0,位置是第三位,由②,③可知正确的号码是5,2,位置分别为第一位和第二位,所以正确的密码是520.
【点睛】本题考查了逻辑推理,根据题意结合所给信息推导出各位数字是解题的关键.
28.见解析
【分析】利用三角形外角的性质得到,再由三角形内角和定理得到,即可证明.
【详解】已知:如图,是的三个外角;
求证:.
证明:∵,
∴,
∵,
∴,
∴命题“三角形不共顶点的三个外角的和等于”是真命题.
【点睛】本题主要考查了证明命题,三角形内角和定理和三角形外角的性质,熟知三角形外角的性质是解题的关键.
29.(1)见解析;(2)当n为奇数时,均可通过“差法”,将用数轴上的点表示
【分析】(1)过原点作射线OA,再以原点O为圆心,用圆规截取一个单位长度为半径画弧交OA为点B,以B为圆心截取两个单位长度为半径画弧交x轴于点C,此时线段OC=;
(2)当n为奇数时,均可通过“差法”,将 用数轴上的点表示;将n为奇数代入证明即可.
【详解】(1)过原点作射线OA,再以原点O为圆心,用圆规截取一个单位长度为半径画弧交OA为点B,以B为圆心截取两个单位长度为半径画弧交x轴于点C,此时线段OC=;
(2)当n为奇数时,均可通过“差法”,将 用数轴上的点表示;
当n为奇数时:
①
②
③
④
……
∴观察可知:差法的前一个数比它后面的数大1,
∴设(x=y+1),
∴
∴ 当n为奇数时,均可通过“差法”,将 用数轴上的点表示.
【点睛】本题考查了作图,并由图观察规律进行证明,正确掌握知识点是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
