2023--2024学年浙教版数学八年级上册2.8直角三角形全等的判定 课件(共17张PPT)
文档属性
| 名称 | 2023--2024学年浙教版数学八年级上册2.8直角三角形全等的判定 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 17:14:28 | ||
图片预览



文档简介
(共17张PPT)
2.8 直角三角形全等的判定
第2章 特殊三角形
浙教版 八年级上册
学习目标
学习目标
a
b
c
1.探索并理解直角三角形全等的判定方法“HL”,理解角平分线性质定理的逆定理.
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
3.掌握角平分线性质定理的逆定理并应用其解题.
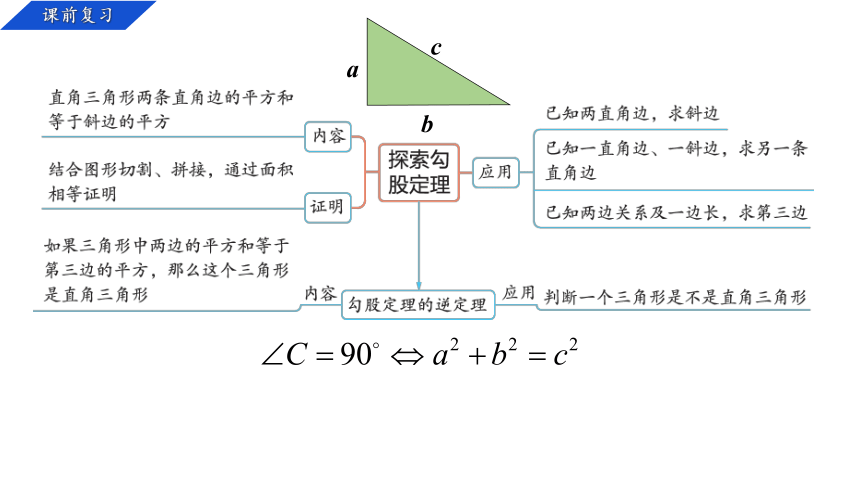
课前复习
a
b
c
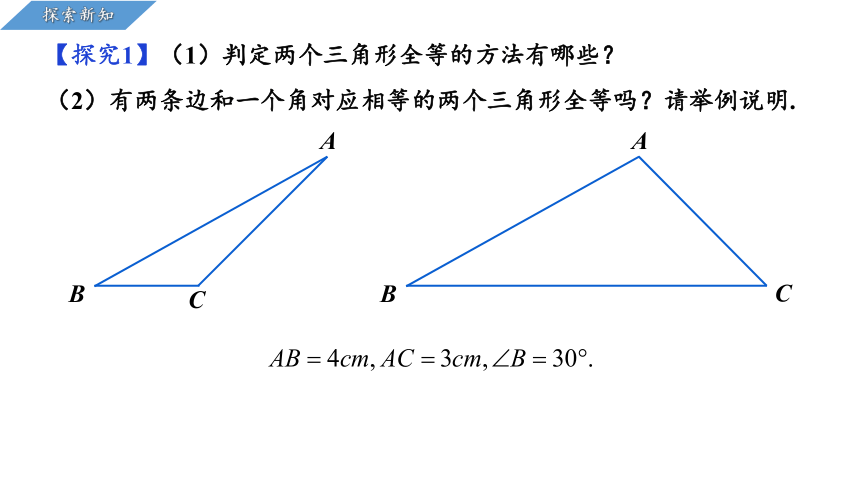
【探究1】(1)判定两个三角形全等的方法有哪些?
(2)有两条边和一个角对应相等的两个三角形全等吗?请举例说明.
探索新知
A
B
C
A
B
C
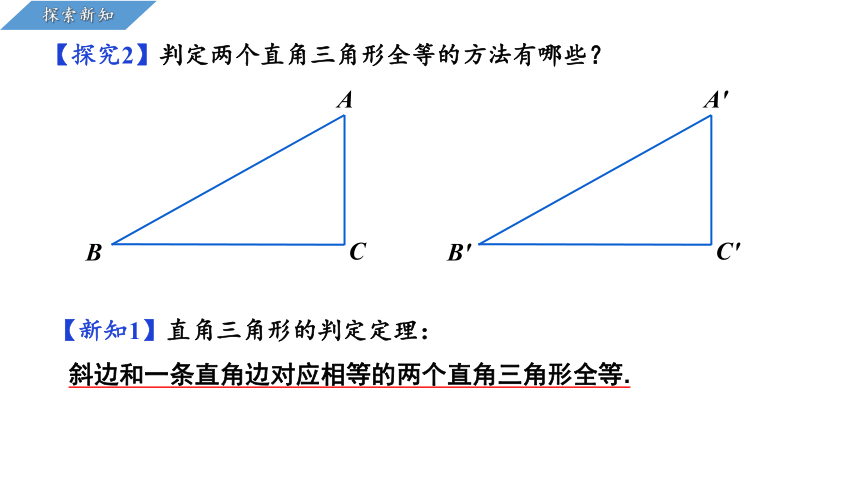
【探究2】判定两个直角三角形全等的方法有哪些?
探索新知
A
B
C
A′
B′
C′
斜边和一条直角边对应相等的两个直角三角形全等.
【新知1】直角三角形的判定定理:
探究新知
A
B
C
A′
B′
C′
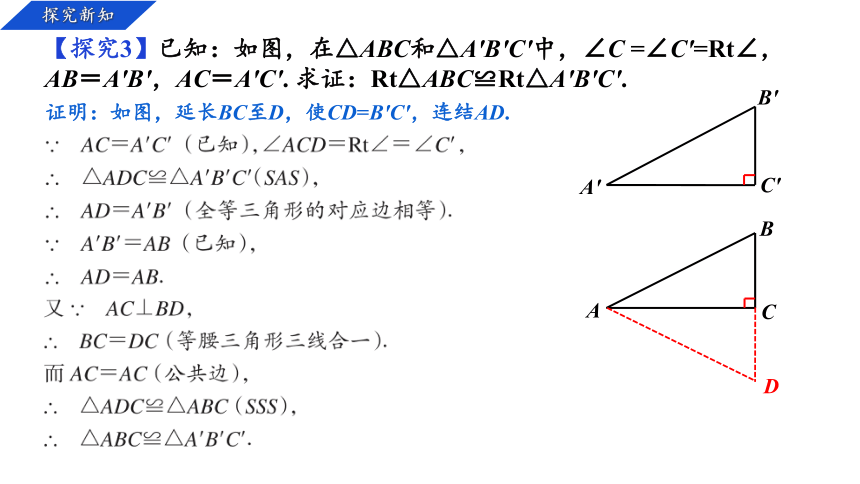
【探究3】已知:如图,在△ABC和△A′B′C′中,∠C =∠C′=Rt∠,
AB=A′B′,AC=A′C′. 求证:Rt△ABC≌Rt△A′B′C′.
证明:如图,延长BC至D,使CD=B′C′,连结AD.
D
新知学习
【新知1】直角三角形全等的判定定理:
(1)文字语言:斜边和一条直角边对应相等的两个直角三角形全等.
(2)符号语言:
A
B
C
A′
B′
C′
(可以简写成“斜边、直角边”或“HL”).
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
∵
【例1】如图,已知P是∠AOB内部一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE,求证:点P在∠AOB的平分线上.
B
O
A
E
P
D
1
2
作射线OP.
解:
∵ PD⊥OA,PE⊥OB
∴ ∠PDO=∠PEO=Rt∠
又∵ OP = OP
PD = PE
∴ Rt△PDO≌ Rt△PEO
∴ ∠1=∠2
即点P在∠AOB的平分线上
(已知)
(已知)
(公共边)
(HL)
(角平分线的定义)
探究新知
新知学习
【新知2】角平分线性质定理的逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上.
符号语言:
∴ 点P在∠AOB的平分线上.
∵
B
O
A
E
P
D
PD⊥OA,PE⊥OB,PD=PE
例题探究
【例2】如图,在△ABC和△A′B′C′中,CD,C′D′分别是两个三角形的高线,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.△ABC与△A′B′C′全等吗?请说明理由.
例题探究
【例3】如图,在等腰直角三角形ABC中,∠ACB=90°,D是斜边AB上任一点,AE⊥CD,垂足为E,BF⊥CD交CD的延长线于点F,CH⊥AB,垂足为H,交AE于点G.问:CG与BD相等吗?请说明理由.
例题探究
【例4】如图2.8 3,在△ABC中,点P在BC边的垂直平分线上,过点P分别作AB,AC(或其延长线)的垂线,垂足分别为M,N,且MB=NC,那么点P在∠BAC的平分线上吗?请说明理由.
课内练习
【1】如图,已知AB=DC,BE⊥AD于点E,CF⊥AD于点F,有下列条件,其中,选择一个就可以判断Rt△ABE≌Rt△DCF的是_______.
①∠B=∠C ②AB∥CD ③BE=CF ④AF=DE
【解析】解:∵BE⊥AD,CF⊥AD,AB=DC,∴∠AEB=∠CFD,选择①可利用AAS定理证明Rt△ABE≌Rt△DCF;选择②可得∠A=∠D,可利用AAS定理证明Rt△ABE≌Rt△DCF;选择③可利用HL定理证明Rt△ABE≌Rt△DCF;选择④可得AE=DF,可利用HL定理证明Rt△ABE≌Rt△DCF.故填:①②③④.
课内练习
【2】如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,求BE的长.
【解析】解:连接CD,BD,∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,∴AE=AF,∵DG是BC的垂直平分线,∴CD=BD,在Rt△CDF和Rt△BDE中,
CD=BD,DF=DE,∴Rt△CDF≌Rt△BDE(HL),∴BE=CF,∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,∵AB=6,AC=4,∴BE=1.
课内练习
【3】已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;(2)线段DM与AM有怎样的位置关系?请说明理由.
【解析】解:(1)AM平分∠DAB,理由为:证明:过点M作ME⊥AD,垂足为E,∵DM平分∠ADC,∴∠1=∠2,∵MC⊥CD,ME⊥AD,∴ME=MC,又∵MC=MB,∴ME=MB,∵MB⊥AB,ME⊥AD,∴AM平分∠DAB.(2)AM⊥DM,理由如下:∵∠B=∠C=90°,∴DC⊥CB,AB⊥CB,∴CD∥AB,∴∠CDA+∠DAB=180°又∵∠1=∠CDA÷2,∠3=∠DAB÷2∴2∠1+2∠3=180°,∴∠1+∠3=90°,∴∠AMD=90度.即AM⊥DM.
E
课内练习
【4】如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm.
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm.
故当AP=5cm或10cm时,△ABC才能和△APQ全等.
斜边和一条直角边对应相等的两个直角三角形全等.
课堂总结
【1】两个直角三角形全等的方法有哪些?
【2】角平分线性质定理的逆定理:
(1)一般三角形判定全等的方法
SAS,ASA,AAS,SSS.
(2)直角三角形全等的判定定理:
(HL)
角的内部,到角两边距离相等的点,在这个角的平分线上.
2.8 直角三角形全等的判定
第2章 特殊三角形
浙教版 八年级上册
学习目标
学习目标
a
b
c
1.探索并理解直角三角形全等的判定方法“HL”,理解角平分线性质定理的逆定理.
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
3.掌握角平分线性质定理的逆定理并应用其解题.
课前复习
a
b
c
【探究1】(1)判定两个三角形全等的方法有哪些?
(2)有两条边和一个角对应相等的两个三角形全等吗?请举例说明.
探索新知
A
B
C
A
B
C
【探究2】判定两个直角三角形全等的方法有哪些?
探索新知
A
B
C
A′
B′
C′
斜边和一条直角边对应相等的两个直角三角形全等.
【新知1】直角三角形的判定定理:
探究新知
A
B
C
A′
B′
C′
【探究3】已知:如图,在△ABC和△A′B′C′中,∠C =∠C′=Rt∠,
AB=A′B′,AC=A′C′. 求证:Rt△ABC≌Rt△A′B′C′.
证明:如图,延长BC至D,使CD=B′C′,连结AD.
D
新知学习
【新知1】直角三角形全等的判定定理:
(1)文字语言:斜边和一条直角边对应相等的两个直角三角形全等.
(2)符号语言:
A
B
C
A′
B′
C′
(可以简写成“斜边、直角边”或“HL”).
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC≌Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
∵
【例1】如图,已知P是∠AOB内部一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE,求证:点P在∠AOB的平分线上.
B
O
A
E
P
D
1
2
作射线OP.
解:
∵ PD⊥OA,PE⊥OB
∴ ∠PDO=∠PEO=Rt∠
又∵ OP = OP
PD = PE
∴ Rt△PDO≌ Rt△PEO
∴ ∠1=∠2
即点P在∠AOB的平分线上
(已知)
(已知)
(公共边)
(HL)
(角平分线的定义)
探究新知
新知学习
【新知2】角平分线性质定理的逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上.
符号语言:
∴ 点P在∠AOB的平分线上.
∵
B
O
A
E
P
D
PD⊥OA,PE⊥OB,PD=PE
例题探究
【例2】如图,在△ABC和△A′B′C′中,CD,C′D′分别是两个三角形的高线,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.△ABC与△A′B′C′全等吗?请说明理由.
例题探究
【例3】如图,在等腰直角三角形ABC中,∠ACB=90°,D是斜边AB上任一点,AE⊥CD,垂足为E,BF⊥CD交CD的延长线于点F,CH⊥AB,垂足为H,交AE于点G.问:CG与BD相等吗?请说明理由.
例题探究
【例4】如图2.8 3,在△ABC中,点P在BC边的垂直平分线上,过点P分别作AB,AC(或其延长线)的垂线,垂足分别为M,N,且MB=NC,那么点P在∠BAC的平分线上吗?请说明理由.
课内练习
【1】如图,已知AB=DC,BE⊥AD于点E,CF⊥AD于点F,有下列条件,其中,选择一个就可以判断Rt△ABE≌Rt△DCF的是_______.
①∠B=∠C ②AB∥CD ③BE=CF ④AF=DE
【解析】解:∵BE⊥AD,CF⊥AD,AB=DC,∴∠AEB=∠CFD,选择①可利用AAS定理证明Rt△ABE≌Rt△DCF;选择②可得∠A=∠D,可利用AAS定理证明Rt△ABE≌Rt△DCF;选择③可利用HL定理证明Rt△ABE≌Rt△DCF;选择④可得AE=DF,可利用HL定理证明Rt△ABE≌Rt△DCF.故填:①②③④.
课内练习
【2】如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,求BE的长.
【解析】解:连接CD,BD,∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,∴AE=AF,∵DG是BC的垂直平分线,∴CD=BD,在Rt△CDF和Rt△BDE中,
CD=BD,DF=DE,∴Rt△CDF≌Rt△BDE(HL),∴BE=CF,∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,∵AB=6,AC=4,∴BE=1.
课内练习
【3】已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;(2)线段DM与AM有怎样的位置关系?请说明理由.
【解析】解:(1)AM平分∠DAB,理由为:证明:过点M作ME⊥AD,垂足为E,∵DM平分∠ADC,∴∠1=∠2,∵MC⊥CD,ME⊥AD,∴ME=MC,又∵MC=MB,∴ME=MB,∵MB⊥AB,ME⊥AD,∴AM平分∠DAB.(2)AM⊥DM,理由如下:∵∠B=∠C=90°,∴DC⊥CB,AB⊥CB,∴CD∥AB,∴∠CDA+∠DAB=180°又∵∠1=∠CDA÷2,∠3=∠DAB÷2∴2∠1+2∠3=180°,∴∠1+∠3=90°,∴∠AMD=90度.即AM⊥DM.
E
课内练习
【4】如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm.
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm.
故当AP=5cm或10cm时,△ABC才能和△APQ全等.
斜边和一条直角边对应相等的两个直角三角形全等.
课堂总结
【1】两个直角三角形全等的方法有哪些?
【2】角平分线性质定理的逆定理:
(1)一般三角形判定全等的方法
SAS,ASA,AAS,SSS.
(2)直角三角形全等的判定定理:
(HL)
角的内部,到角两边距离相等的点,在这个角的平分线上.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
