2.6 探索勾股定理（1）

课件28张PPT。2.6 勾股定理（1)义务教育课程标准实验教科书　
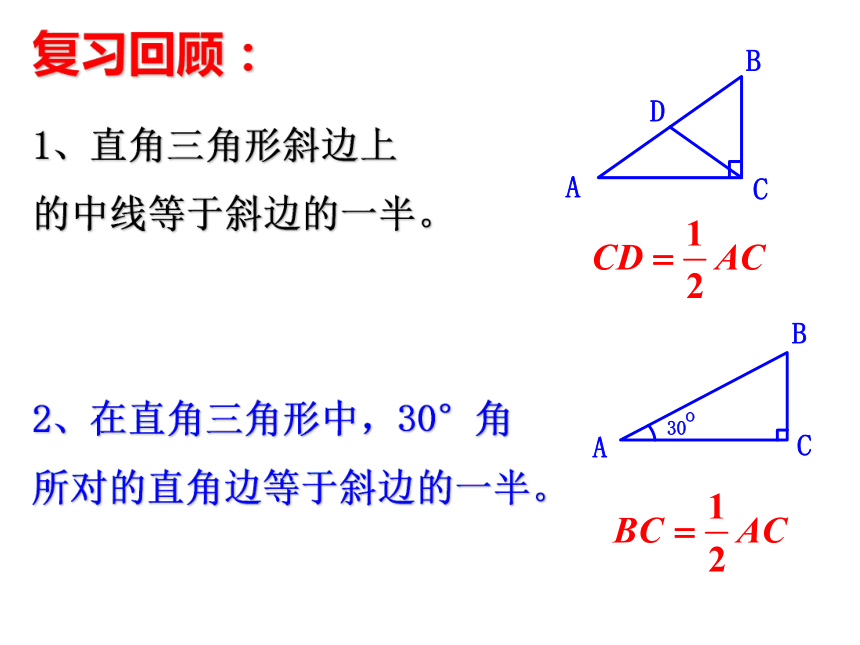
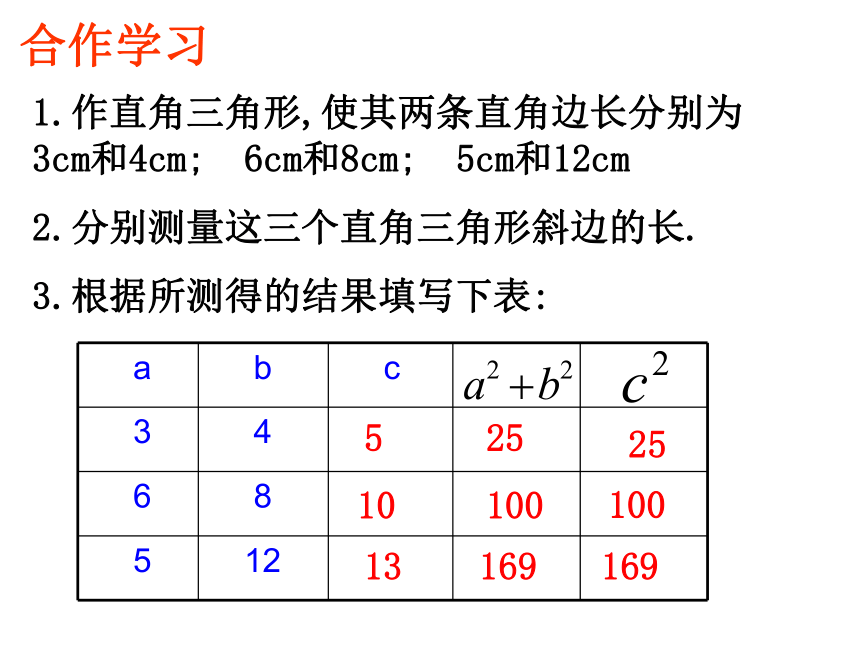
浙江版《数学》八年级上册复习回顾： 在《九章算术》中记载了一道有趣的数学题：“今有池方一丈，葭生其中央．出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何？”这道题的意思是说：有一个边长为1丈的正方形水池，在池的中央长着一根芦苇，芦苇露出水面1尺。若将芦苇拉到池边中点处，芦苇的顶端恰好到达水面。问水有多深？芦苇有多长？51合作学习1.作直角三角形,使其两条直角边长分别为 3cm和4cm; 6cm和8cm; 5cm和12cm
2.分别测量这三个直角三角形斜边的长.
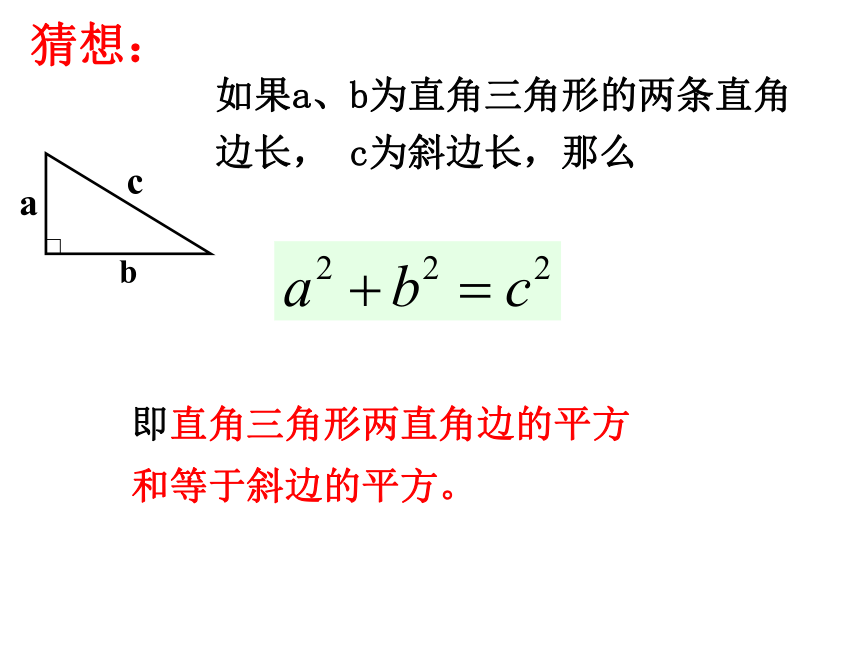
3.根据所测得的结果填写下表:525251010010013169169猜想：如果a、b为直角三角形的两条直角边长， c为斜边长，那么即直角三角形两直角边的平方和等于斜边的平方。拼图游戏:
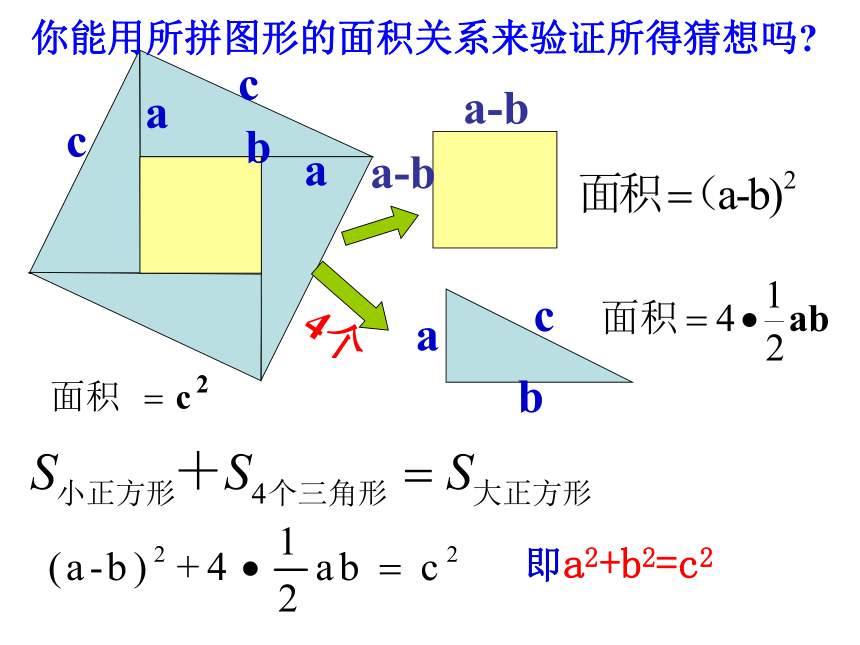
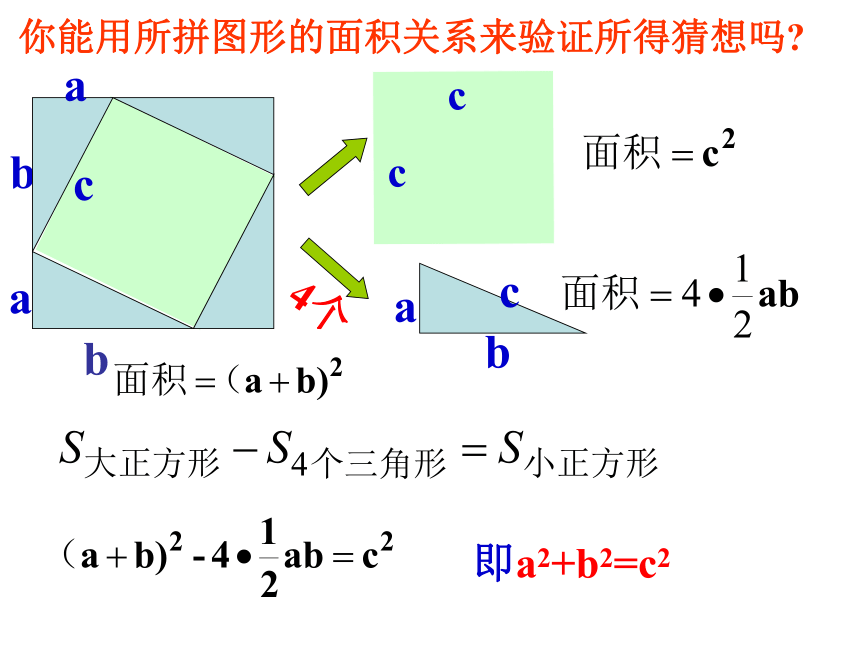
给定四个全等的直角三角形纸片,假设三角形的两直角边分别为a、b，斜边为c。你们能用这四个三角形纸片，围出一个正方形吗?abcca即a2+b2=c2 你能用所拼图形的面积关系来验证所得猜想吗?即a2+b2=c2 你能用所拼图形的面积关系来验证所得猜想吗?勾股定理　　如果直角三角形两直角边分别为a、b，斜边为c，那么　　即 直角三角形两直角边的平方和等于斜边的平方．中国古代数学家——赵爽的验证方法 还可以认为是四个三角形与一个小正方形的和，即2002年在北京召开的国际数学家大会的会标就是依据我国古代数学家赵爽的弦图制作的。∴∵毕达哥拉斯 在国外，相传勾股定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”，埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 商高是公元前十一世纪(西周)的中国人。在大约战国时期西汉的数学著作 《周髀 算经》中记录着商高同周公的一段对话。商高说：“…故折矩，勾广三，股修四，经隅五。” 后来人们就简单地把这个事实说成“勾三股四弦五”。这就是著名的勾股定理. 世界上几个文明古国都对勾股定理的发现作出过自己的贡献。大约成书于公元前2世纪的我国天文学著作《周髀》（后人改称《周髀算经》）中，记载了“勾三、股四、弦五”（如图），勾股定理在国外又称毕达哥拉斯定理，相传是古希腊数学家毕达哥拉斯发现的。 勾股定理史话 在漫长的岁月中，人们对勾股定理创造了形形色色的奇妙的证明方法，据不完全统计，目前已有370多种不同证法。例1 、已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=C
已知: a=1, b=2, 求c;
已知: a=15, c=17, 求b; abc解:(1)根据勾股定理得:c2=a2+b2=12 +22 =5(2)根据勾股定理得:∵b>0 , ∴b=8=172 -152=64=(17＋15)(17－15)b2 = c2 -a2 练一练 解：设a＝8x，则b＝15x(x>0)∵a2+b2=c2∴(8x)2+(15x)2=342∴x2=4∵x>0,∴x=2∴ a＝16，b＝30温馨提示：学会用方程来解决几何问题2、在《九章算术》中记载了一道有趣的数学题：“今有池方一丈，葭生其中央．出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何？”这道题的意思是说：有一个边长为1丈的正方形水池，在池的中央长着一根芦苇，芦苇露出水面1尺。若将芦苇拉到池边中点处，芦苇的顶端恰好到达水面。问水有多深？芦苇有多长？xX+1设水深x尺，则芦苇长(x+1)尺，X2+52=(x+1)23、求下列图中字母所代表的正方形面积：3260AB225814、若△ABC的两边为3和4，你能求出第三边吗？为什么？若Rt△ABC的两边为3和4，求第三边的长。注意要进行分类讨论32 6、今年夏天，受台风“桑美”影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？
你会算吗? 试试看！例2、如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离。ABC409016040解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。 AC=90-40=50(mm),BC=160-40=120(mm).∵ ∠C =90。∴ AB2=AC2+BC2 ∵AB>0∴AB=130(mm)答:两孔中心A,B之间的距离为130mm.说说你对本题的收获 温馨提示：在实际问题中，要会根据需要构造直角三角形，再通过勾股定理来解决问题=502+1202 =16900(mm2) 1、飞机在空中水平飞行，某一时刻刚好飞到一个男孩头顶上方4000米处，过了20秒，飞机距离这个男孩头顶5000米。飞机每时飞行多少千米？ABC试一试 2、某同学的妈妈买了一部29英寸（74厘米）的电视机。该同学量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你认为售货员搞错了吗？为什么？∴售货员没搞错解：∵荧屏对角线大约为74厘米温馨提示：我们通常所说的29英寸或74厘米的 电视机，是指其荧屏对角线的长度.∴ AB2=AC2+BC2∴AB2= 462+582 = 5480∴AB≈74厘米4658ABC∵∠C=90°741.勾股定理的内容2.勾股定理的证明方法3.勾股定理在生活中的应用4.探究—猜想—归纳—推理的数学思想你说我说大家说请你谈谈通过本节课的学习你学到了什么!(1)求墙的高度? （精确到0.1米）解：∵∠ACB=90°AB=3，BC=1≈2.8(米)(2)若梯子的顶端下滑50厘米,
底端将向外水平移动多少米?AA′BB′3m1mC∴ AB2=AC2+BC2 有一架3米长的梯子靠在墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。探究1 做一个长，宽，高分别为50厘米，40厘米，30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明。探究2如图，在△ABC中，AB=AC。已知AB=17，BC=16。(1)求BC边上的中线AD的长。(2)求△ABC的面积。(3)过点B作BE⊥AC，垂足为E，求BE的长。探究3再见！