第3章圆的基本性质专题3.5 圆周角定理【十大题型】(含解析)
文档属性
| 名称 | 第3章圆的基本性质专题3.5 圆周角定理【十大题型】(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-18 15:59:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
圆周角定理10大题型
TOC \o "1-3" \h \u
HYPERLINK \l "_Toc24819" 【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】 2
HYPERLINK \l "_Toc32120" 【题型2 同弧或等弧所对的圆周角相等的运用】 5
HYPERLINK \l "_Toc2689" 【题型3 直径所对的圆周角是90°的运用】 9
HYPERLINK \l "_Toc21132" 【题型4 翻折中的圆周角的运用】 13
HYPERLINK \l "_Toc10283" 【题型5 利用圆周角求最值】 18
HYPERLINK \l "_Toc27772" 【题型6 圆周角中的证明】 22
HYPERLINK \l "_Toc9392" 【题型7 圆周角中的多结论问题】 28
HYPERLINK \l "_Toc11917" 【题型8 构造圆利用圆周角解决三角形或四边形中的问题】 32
HYPERLINK \l "_Toc29627" 【题型9 圆周角与量角器的综合运用】 37
HYPERLINK \l "_Toc19793" 【题型10 利用圆周角求取值范围】 40
【知识点1 圆周角定理及其推论】
圆周角定理 定理:圆周角的度数等于它所对的弧的圆心角度数的一半 是所对的圆心角,是所对的圆周角,
推论1:同弧或等弧所对的圆周角相等 和都是所对的圆周角
推论2:直径所对的圆周角是直角,的圆周角所对的弦是直径 是的直径是所对的圆周角是所对的圆周角 是的直径
【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】
【例1】(2022 鼓楼区校级模拟)如图,CD是⊙O的直径,⊙O上的两点A,B分别在直径CD的两侧,且∠ABC=78°,则∠AOD的度数为( )
A.12° B.22° C.24° D.44°
【变式1-1】(2022 温州)如图,AB,AC是⊙O的两条弦,OD⊥AB于点D,OE⊥AC于点E,连结OB,OC.若∠DOE=130°,则∠BOC的度数为( )
A.95° B.100° C.105° D.130°
【变式1-2】(2022 蓝山县一模)如图,点A,B,C在⊙O上,∠1=40°,∠C=25°,则∠B=( )
A.100° B.70° C.55° D.65°
【变式1-3】(2022春 汉阳区校级月考)如图,AB,CD为⊙O的两条弦,若∠A+∠C=120°,AB=2,CD=4,则⊙O的半径为( )
A.2 B.2 C. D.
【题型2 同弧或等弧所对的圆周角相等的运用】
【例2】(2022 保亭县二模)如图,AB为⊙O的直径,点C、D在圆上,CE⊥AB于点E,若∠D=48°,则∠1=( )
A.42° B.45° C.48° D.52°
【变式2-1】(2022 南充)如图,AB为⊙O的直径,弦CD⊥AB于点E,OF⊥BC于点F,∠BOF=65°,则∠AOD为( )
A.70° B.65° C.50° D.45°
【变式2-2】(2022 十堰二模)如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以BC为直径的⊙O交AB于点D.E是⊙O上一点,且,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
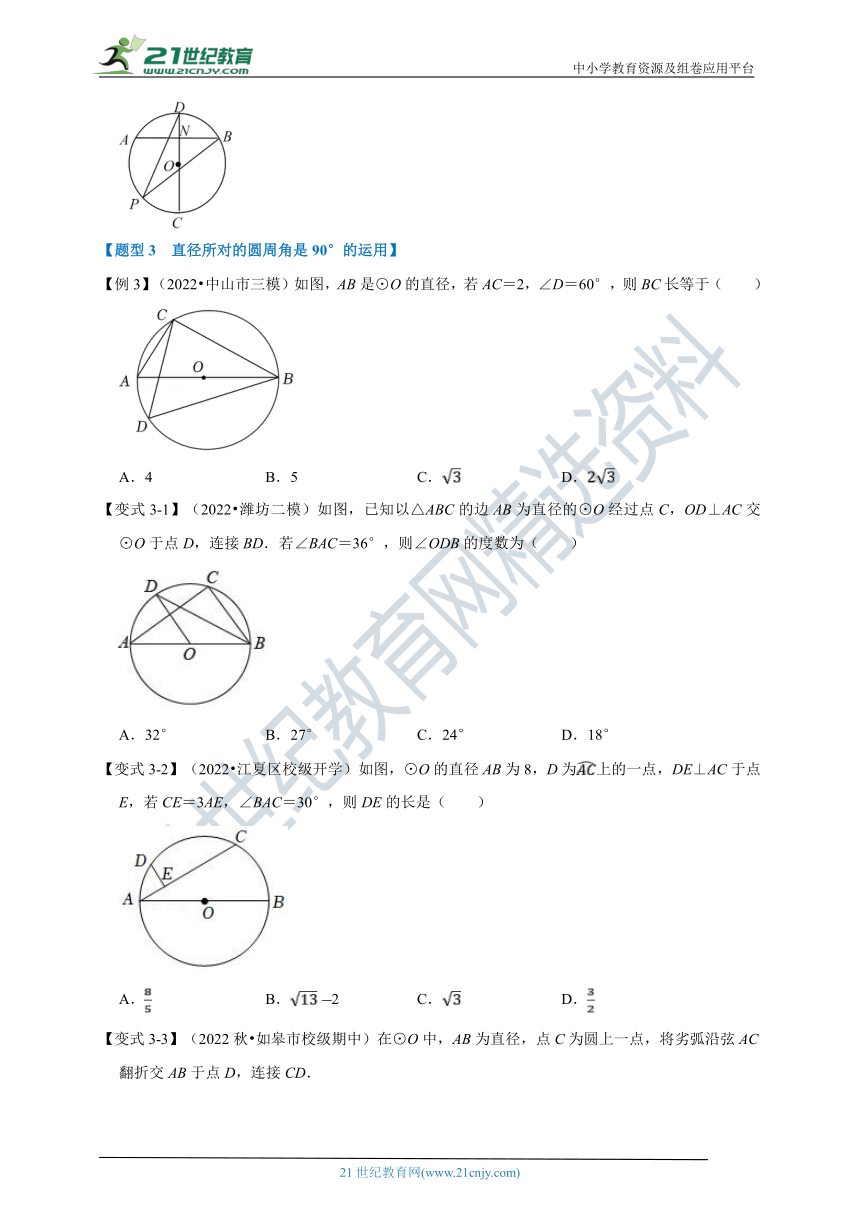
【变式2-3】(2022 本溪模拟)如图,在⊙O中,,直径CD⊥AB于点N,P是上一点,则∠BPD的度数是 .
【题型3 直径所对的圆周角是90°的运用】
【例3】(2022 中山市三模)如图,AB是⊙O的直径,若AC=2,∠D=60°,则BC长等于( )
A.4 B.5 C. D.
【变式3-1】(2022 潍坊二模)如图,已知以△ABC的边AB为直径的⊙O经过点C,OD⊥AC交⊙O于点D,连接BD.若∠BAC=36°,则∠ODB的度数为( )
A.32° B.27° C.24° D.18°
【变式3-2】(2022 江夏区校级开学)如图,⊙O的直径AB为8,D为上的一点,DE⊥AC于点E,若CE=3AE,∠BAC=30°,则DE的长是( )
A. B.2 C. D.
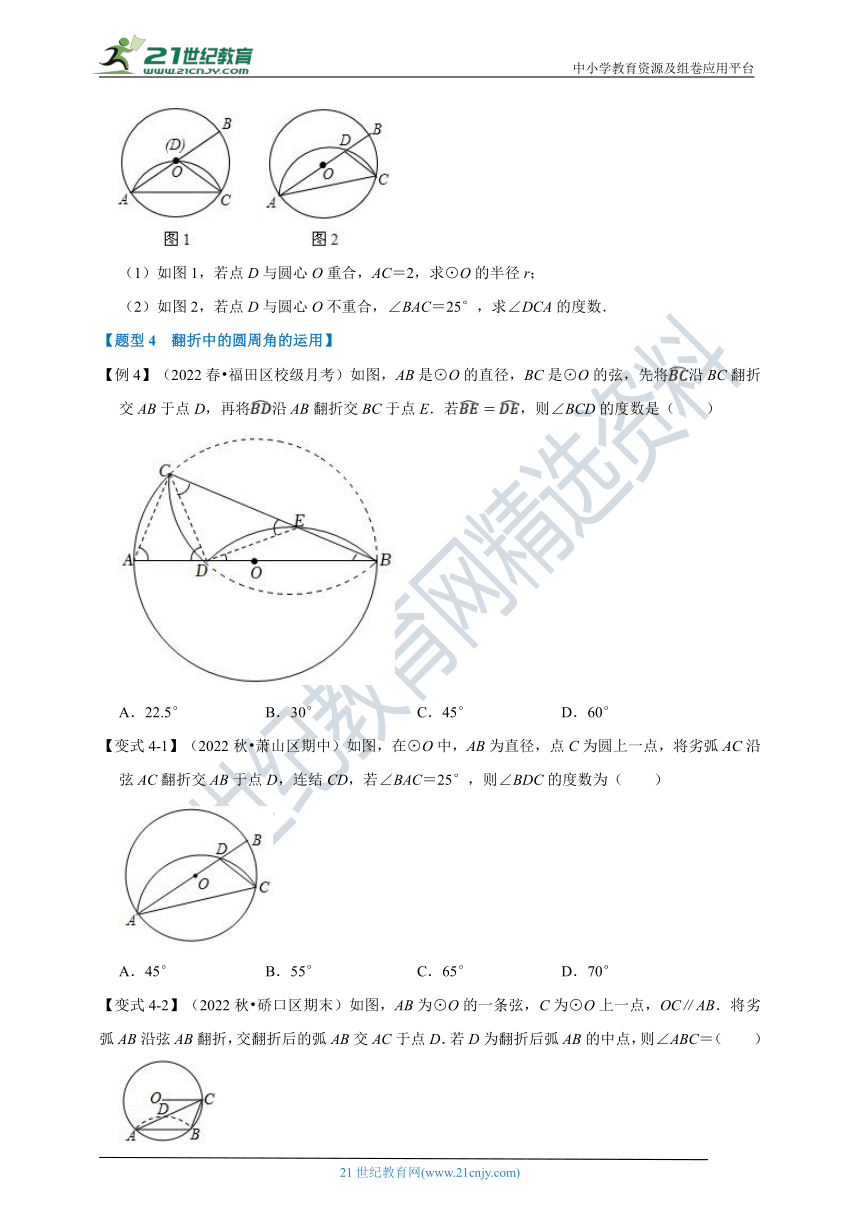
【变式3-3】(2022秋 如皋市校级期中)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
【题型4 翻折中的圆周角的运用】
【例4】(2022春 福田区校级月考)如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若,则∠BCD的度数是( )
A.22.5° B.30° C.45° D.60°
【变式4-1】(2022秋 萧山区期中)如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D,连结CD,若∠BAC=25°,则∠BDC的度数为( )
A.45° B.55° C.65° D.70°
【变式4-2】(2022秋 硚口区期末)如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=( )
A.110° B.112.5° C.115° D.117.5°
【变式4-3】(2022秋 丹江口市期中)已知⊙O的直径AB长为10,弦CD⊥AB,将⊙O沿CD翻折,翻折后点B的对应点为点B′,若AB′=6,CB′的长为( )
A. B.或 C. D.或
【题型5 利用圆周角求最值】
【例5】(2022 瑶海区三模)如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
【变式5-1】(2022 陈仓区一模)如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
【变式5-2】(2022秋 大连期末)如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为的中点,E是直径AB上一动点,则CE+DE最小值为( )
A.1 B. C. D.2
【变式5-3】(2022 杏花岭区校级三模)如图,矩形ABCD中,AB,BC=AB2,E为射线BA上一动点,连接CE交以BE为直径的圆于点H,则线段DH长度的最小值为 .
【题型6 圆周角中的证明】
【例6】(2022秋 定陶区期末)如图1.在⊙O中AB=AC,∠ACB=70°,点E在劣弧上运动,连接EC,BE,交AC于点F.
(1)求∠E的度数;
(2)当点E运动到使BE⊥AC时,连接AO并延长,交BE于点D,交BC于点G,交⊙O于点M,依据题意在备用图中画出图形.并证明:G为DM的中点.
【变式6-1】(2022春 金山区校级月考)已知CD为⊙O的直径,A、B为⊙O上两点,点C为劣弧AB中点,连接DA、BA、AC,且∠B=30°.
(1)求证:∠D=30°;
(2)F、G分别为线段CD、AC上两点,满足DF=AG,连接AF、OG,取OG中点H,连接CH,请猜测AF与CH之间的数量关系,并证明.
【变式6-2】(2022 武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE的形状,并证明你的结论;
(2)若AB=10,BE=2,求BC的长.
【变式6-3】(2022 南召县四模)阅读下面材料,完成相应的任务:
阿基米德是有史以来最伟大的数学家之一、《阿基米德全集》收集了已发现的阿基米德著作,它对于了解古希腊数学,研究古希腊数学思想以及整个科技史都是十分宝贵的.其中论述了阿基米德折弦定理:从圆周上任一点出发的两条弦,所组成的折线,称之为该圆的一条折弦.一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影,就是折弦的中点.
如图1,AB和BC是⊙O的两条弦(即ABC是圆的一条折弦),BC>AB.M是弧ABC的中点,则从M向BC所作垂线之垂足D是折弦ABC的中点,即CD=AB+BD.
小明认为可以利用“截长法”,如图2:在线段CB上从C点截取一段线段CN=AB,连接MA,MB,MC,MN.
小丽认为可以利用“垂线法”,如图3:过点M作MH⊥AB于点H,连接MA,MB,MC.
任务:(1)请你从小明和小丽的方法中任选一种证明思路,继续书写出证明过程.
(2)就图3证明:MC2﹣MB2=BC AB.
【题型7 圆周角中的多结论问题】
【例7】(2022 兰陵县二模)如图,在⊙O中,AB是⊙O的直径,AB=10,,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
【变式7-1】(2022秋 淅川县期末)如图,已知:点A、B、C、D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
A.2 B.3 C.4 D.5
【变式7-2】(2022秋 厦门期末)在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D.要使得⊙O与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是 .(写出所有正确答案的序号)
①∠BAC>60°;②45°<∠ABC<60°;③BDAB;④AB<DEAB.
【变式7-3】(2022秋 东台市月考)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是 .(填序号)
【题型8 构造圆利用圆周角解决三角形或四边形中的问题】
【例8】(2022春 杏花岭区校级月考)如图,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴正半轴上,且∠ACB=45°,则点C的坐标为( )
A.(0,7) B.(0,2) C.(0,6) D.(0,3)
【变式8-1】(2022秋 秦淮区期末)如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= °.
【变式8-2】(2022 北京模拟)已知三角形ABC是锐角三角形,其中∠A=30°,BC=4,设BC边上的高为h,则h的取值范围是 .
【变式8-3】(2022春 西湖区校级月考)已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为 .
【题型9 圆周角与量角器的综合运用】
【例9】(2022 南召县模拟)以O为中心点的量角器与直角三角板ABC按如图方式摆放,量角器的0刻度线与斜边AB重合.点D为斜边AB上一点,作射线CD交弧AB于点E,如果点E所对应的读数为50°,那么∠BDE的大小为( )
A.100° B.110° C.115° D.130°
【变式9-1】(2022秋 南京期中)将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆圆心上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A= .
【变式9-2】(2022秋 高港区期中)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应的刻度值为50°,则∠BCD的度数为 .
【变式9-3】(2022秋 北京期末)如图,量角器的直径与直角三角尺ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,则第20秒点E在量角器上对应的读数是 °.
【题型10 利用圆周角求取值范围】
【例10】(2022 观山湖区模拟)如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是 .
【变式10-1】(2022 河南三模)如图,点O是以AC为直径的半圆的圆心,点B在上,∠ACB=30°,AC=2.点D是直径AC上一动点(与点A,C不重合),记OD的长为m.连接BD,点A关于BD的对称点为点A′,当点A′落在由直径AC,弦围成的封闭图形内部时(不包含边界),m的取值范围是 .
【变式10-2】(2022秋 台州期中)如图,已知AB是⊙O的一条弦,点C是⊙O的优弧ACB上的一个动点(不与A,B不重合),
(1)设∠ACB的平分线与劣弧AB交于点P,试猜想点P劣弧AB上的位置是否会随点C的运动而变化?请说明理由
(2)如图②,设AB=8,⊙O的半径为5,在(1)的条件下,四边形ACBP的面积是否为定值?若是定值,请求出这个定值;若不是定值,请求出ACBP的面积的取值范围.
【变式10-3】(2022秋 高新区校级期末)如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB是⊙O上关于A、B的滑动角.若⊙O的半径是1,AB,则∠APB的取值范围为 .
圆周角定理【十大题型】
TOC \o "1-3" \h \u
HYPERLINK \l "_Toc24819" 【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】 2
HYPERLINK \l "_Toc32120" 【题型2 同弧或等弧所对的圆周角相等的运用】 5
HYPERLINK \l "_Toc2689" 【题型3 直径所对的圆周角是90°的运用】 9
HYPERLINK \l "_Toc21132" 【题型4 翻折中的圆周角的运用】 13
HYPERLINK \l "_Toc10283" 【题型5 利用圆周角求最值】 18
HYPERLINK \l "_Toc27772" 【题型6 圆周角中的证明】 22
HYPERLINK \l "_Toc9392" 【题型7 圆周角中的多结论问题】 28
HYPERLINK \l "_Toc11917" 【题型8 构造圆利用圆周角解决三角形或四边形中的问题】 32
HYPERLINK \l "_Toc29627" 【题型9 圆周角与量角器的综合运用】 37
HYPERLINK \l "_Toc19793" 【题型10 利用圆周角求取值范围】 40
【知识点1 圆周角定理及其推论】
圆周角定理 定理:圆周角的度数等于它所对的弧的圆心角度数的一半 是所对的圆心角,是所对的圆周角,
推论1:同弧或等弧所对的圆周角相等 和都是所对的圆周角
推论2:直径所对的圆周角是直角,的圆周角所对的弦是直径 是的直径是所对的圆周角是所对的圆周角 是的直径
【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】
【例1】(2022 鼓楼区校级模拟)如图,CD是⊙O的直径,⊙O上的两点A,B分别在直径CD的两侧,且∠ABC=78°,则∠AOD的度数为( )
A.12° B.22° C.24° D.44°
【分析】利用圆周角定理求出∠AOC=156°,可得结论.
【解答】解:∵∠AOC=2∠ABC,∠ABC=78°,
∴∠AOC=156°,
∴∠AOD=180°﹣∠AOC=24°,
故选:C.
【变式1-1】(2022 温州)如图,AB,AC是⊙O的两条弦,OD⊥AB于点D,OE⊥AC于点E,连结OB,OC.若∠DOE=130°,则∠BOC的度数为( )
A.95° B.100° C.105° D.130°
【分析】根据四边形的内角和等于360°计算可得∠BAC=50°,再根据圆周角定理得到∠BOC=2∠BAC,进而可以得到答案.
【解答】解:∵OD⊥AB,OE⊥AC,
∴∠ADO=90°,∠AEO=90°,
∵∠DOE=130°,
∴∠BAC=360°﹣90°﹣90°﹣130°=50°,
∴∠BOC=2∠BAC=100°,
故选:B.
【变式1-2】(2022 蓝山县一模)如图,点A,B,C在⊙O上,∠1=40°,∠C=25°,则∠B=( )
A.100° B.70° C.55° D.65°
【分析】根据圆周角定理得出∠BOC=2∠1=80°,根据三角形内角和定理得出∠1+∠B+∠ADB=180°,∠C+∠BOC+∠ODC=180°,求出∠1+∠B=∠BOC+∠C即可.
【解答】解:设OB交AC于D,
∵∠1=40°,
∴∠BOC=2∠1=80°,
∵∠1+∠B+∠ADB=180°,∠C+∠BOC+∠ODC=180°,∠ADB=∠ODC,
∴∠1+∠B=∠BOC+∠C,
∵∠C=25°,
∴40°+∠B=80°+25°,
∴∠B=65°,
故选:D.
【变式1-3】(2022春 汉阳区校级月考)如图,AB,CD为⊙O的两条弦,若∠A+∠C=120°,AB=2,CD=4,则⊙O的半径为( )
A.2 B.2 C. D.
【分析】连接OB,OA,OC,OD,证明∠AOB+∠COD=90°,在⊙O上点D的右侧取一点E,使得DE=AB,过点E作ET⊥CD交CD的延长线于点T,则,利用勾股定理求解即可.
【解答】解:如图,连接OB,OA,OC,OD,
∵∠BOC=2∠CAB,∠AOD=2∠ACD,∠CAB+∠ACD=120°,
∴∠BOC+∠AOD=240°,
∴∠AOB+∠COD=120°,
在⊙O上点D的右侧取一点E,使得DE=AB,过点E作ET⊥CD交CD的延长线于点T,则,
∴∠AOB=∠DOE,
∴∠COE=120°,
∴∠CDE=120°,
∴∠EDT=60°,
∵DE=AB=2,
∴DT=1,ET,
∴CT=CD+DT=4+1=5,
∴CE,
作OF⊥CE,则∠COF=60°,CF,
∴OC=OE,
故选:D.
【题型2 同弧或等弧所对的圆周角相等的运用】
【例2】(2022 保亭县二模)如图,AB为⊙O的直径,点C、D在圆上,CE⊥AB于点E,若∠D=48°,则∠1=( )
A.42° B.45° C.48° D.52°
【分析】连接AC,根据圆周角定理得出∠A=∠D=48°,∠ACB=90°,求出∠ABC,根据垂直求出∠CEB,再求出∠1即可.
【解答】解:连接AC,
由圆周角定理得:∠A=∠D,
∵∠D=48°,
∴∠A=48°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC=90°﹣∠A=42°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠1=90°﹣∠ABC=48°,
故选:C.
【变式2-1】(2022 南充)如图,AB为⊙O的直径,弦CD⊥AB于点E,OF⊥BC于点F,∠BOF=65°,则∠AOD为( )
A.70° B.65° C.50° D.45°
【分析】先根据三角形的内角和定理可得∠B=25°,由垂径定理得:,最后由圆周角定理可得结论.
【解答】解:∵OF⊥BC,
∴∠BFO=90°,
∵∠BOF=65°,
∴∠B=90°﹣65°=25°,
∵弦CD⊥AB,AB为⊙O的直径,
∴,
∴∠AOD=2∠B=50°.
故选:C.
【变式2-2】(2022 十堰二模)如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以BC为直径的⊙O交AB于点D.E是⊙O上一点,且,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
【分析】连接OD,根据圆心角、弧、弦之间的关系得出∠DOC=∠EOC,根据直角三角形的两锐角互余得出∠B=90°﹣∠A=36°,根据圆周角定理求出∠DOC=2∠B=72°,求出∠EOC=∠DOC=72°,再根据四边形的内角和等于360°求出即可.
【解答】解:解法一、连接OD,
∵,
∴∠DOC=∠EOC,
∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∴∠DOC=2∠B=72°,
∴∠EOC=∠DOC=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
解法二、∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∵,
∴∠COE=2∠B=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
故选:B.
【变式2-3】(2022 本溪模拟)如图,在⊙O中,,直径CD⊥AB于点N,P是上一点,则∠BPD的度数是 30° .
【分析】连接OA、OB,如图,先根据垂径定理得到,所以,利用圆心角、弧、弦的关系得到∠AOC=∠BOC=∠AOB=120°,所以∠BOD=60°,然后根据圆周角定理求解.
【解答】解:连接OA、OB,如图,
∵CD⊥AB,
∴,
∵,
∴,
∴∠AOC=∠BOC=∠AOB360°=120°,
∴∠BOD=180°﹣120°=60°,
∴∠BPD∠BOD=30°.
故答案为:30°.
【题型3 直径所对的圆周角是90°的运用】
【例3】(2022 中山市三模)如图,AB是⊙O的直径,若AC=2,∠D=60°,则BC长等于( )
A.4 B.5 C. D.
【分析】根据圆周角定理得出∠ACB=90°,∠CAB=∠D=60°,求出∠ABC=90°﹣∠CAB=30°,根据含30度角的直角三角形的性质求出AB=2AC=4,再根据勾股定理求出BC即可.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠D=60°,
∴∠CAB=∠D=60°,
∴∠ABC=90°﹣∠CAB=30°,
∵AC=2,
∴AB=2AC=4,
∴BC2,
故选:D.
【变式3-1】(2022 潍坊二模)如图,已知以△ABC的边AB为直径的⊙O经过点C,OD⊥AC交⊙O于点D,连接BD.若∠BAC=36°,则∠ODB的度数为( )
A.32° B.27° C.24° D.18°
【分析】设AC与OD相交于点E,根据直径所对的圆周角是直角可得∠ACB=90°,从而求出∠ABC=54°,再根据垂直定义可得∠AEO=90°,从而可得OD∥BC,然后利用等腰三角形和平行线的性质可得BD平分∠ABC,即可解答.
【解答】解:设AC与OD相交于点E,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=36°,
∴∠ABC=90°﹣∠BAC=54°,
∵OD⊥AC,
∴∠AEO=90°,
∴∠AEO=∠ACB=90°,
∴OD∥BC,
∴∠ODB=∠DBC,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠OBD=∠DBC∠ABC=27°,
∴∠ODB=∠OBD=27°,
故选:B.
【变式3-2】(2022 江夏区校级开学)如图,⊙O的直径AB为8,D为上的一点,DE⊥AC于点E,若CE=3AE,∠BAC=30°,则DE的长是( )
A. B.2 C. D.
【分析】在30°的直角三角形ABC中求出AC=4,根据CE=3AE得到AE,再分别求出DF、ME、MF的长度即可得解.
【解答】解:如图,连接连接BC、OD,作OF⊥DE,交DE的延长线于点F,DF、AB交于点M
∵AB为直径,
∴∠ACB=90°,
又∵∠BAC=30°,
∴BC=4,AC=4,
∵CE=3AE,
∴AE,
∵DE⊥AC,∠BAC=30°,
∴EM=1,AM=2,
∴OM=OA﹣AM=4﹣2=2,
在Rt△OMF中,
∵∠OFM=90°,∠OMF=∠AME=90°﹣30°=60°,OM=2,
∴MF=1,OF,
∵∠F=90°,
∴DF,
∴DE=DF﹣ME﹣MF.
故选:B.
【变式3-3】(2022秋 如皋市校级期中)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
【分析】(1)过点O作OE⊥AC于E,由垂径定理可知AEAC2=1,根据翻折后点D与圆心O重合,可知OEr,在Rt△AOE中,根据勾股定理可得出r的值;
(2)连接BC,根据直径所对的圆周角是直角求出∠ACB,根据直角三角形两锐角互余求出∠B,再根据翻折的性质得到所对的圆周角,然后根据∠ACD等于所对的圆周角减去所对的圆周角,计算即可得解.
【解答】解:(1)如图1,过点O作OE⊥AC于E
则AEAC2=1,
∵翻折后点D与圆心O重合,
∴OEr,
在Rt△AOE中,AO2=AE2+OE2,
即r2=12+(r)2,解得r;
(2)连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质,所对的圆周角为∠B,所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.
【题型4 翻折中的圆周角的运用】
【例4】(2022春 福田区校级月考)如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若,则∠BCD的度数是( )
A.22.5° B.30° C.45° D.60°
【分析】证明∠CAB=3α,利用三角形内角和定理求出α,可得结论.
【解答】解:设∠ABC=α,
则,,的度数都为2α,
∴的度数=4α,
∵翻折,
∴的度数=4α,
∴的度数=2α+4α=6α,
∵的度数的度数=180°,
∴2α+6α=180°,
∴α=22.5°.
∴的度数=90°
∴∠BCD=45°.
故选:C.
【变式4-1】(2022秋 萧山区期中)如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D,连结CD,若∠BAC=25°,则∠BDC的度数为( )
A.45° B.55° C.65° D.70°
【分析】解法一、补齐翻折后的弧为圆⊙P,根据圆周角定理得出,求出∠BDC=∠DBC,根据圆周角定理求出∠ACB=90°,再求出∠ABC即可;解法二、过D作DE⊥AC于E,延长DE交⊙O于F,连接AF、CF、BC,根据圆周角定理得出∠ACB=90°,根据翻折变换得出∠FAC=∠BAC=25°,∠DCA=∠FCA,根据圆内接四边形的性质得出∠BAF+∠BCF=180°,求出∠ACF=40°,求出∠ACD=∠ACF=40°,再根据三角形的外角性质求出即可.
【解答】解:解法一、补齐翻折后的弧为圆⊙P
则⊙O和⊙P为等圆,
∵∠BAC在⊙O和⊙P中分别对应弧BC和弧DC,
∴(在同圆或等圆中,相等的圆周角所对的弧相等),
∴BC=DC,
∴∠BDC=∠DBC,
∵AB为⊙O直径,
∴∠DBC=90°﹣∠BAC=65°,
∴∠BDC=65°;
解法二、过D作DE⊥AC于E,延长DE交⊙O于F,连接AF、CF、BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵将劣弧AC沿弦AC翻折交AB于点D,连结CD,∠BAC=25°,
∴∠FAC=∠BAC=25°,∠DCA=∠FCA,
∵点A、F、C、B四点共圆,
∴∠BAF+∠BCF=180°,
∴25°+25°+90°+∠ACF=180°,
解得:∠ACF=40°,
即∠ACD=∠ACF=40°,
∵∠BAC=25°,
∴∠BDC=∠BAC+∠ACD=25°+40°=65°,
故选:C.
【变式4-2】(2022秋 硚口区期末)如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=( )
A.110° B.112.5° C.115° D.117.5°
【分析】如图,连接OA,OB,BD.设∠DAB=x.用x表示出∠BDC,∠BCD,∠DBC,利用三角形内角和定理,构建方程求解.
【解答】解:如图,连接OA,OB,BD.设∠DAB=x.
∵,
∴DA=DB,
∵,
∴BD=CD,
∴∠DAB=∠DBA=x,∠BDC=∠BCD=∠DAB+∠ABD=2x,
∵OC∥AB,
∴∠OCA=∠DAB=x,
∵OA=OC=OB,
∴∠OCB=∠OBC=3x,∠OAD=∠OCA=x,∠OAB=∠OBA=2x,
∴∠OBD=x,
∴∠CBD=4x,
在△BDC中,∠BDC+∠DCB+∠DBC=180°,
∴2x+2x+4x=180°,
∴x=22.5°,
∴∠ABC=5x=112.5°,
故选:B.
【变式4-3】(2022秋 丹江口市期中)已知⊙O的直径AB长为10,弦CD⊥AB,将⊙O沿CD翻折,翻折后点B的对应点为点B′,若AB′=6,CB′的长为( )
A. B.或 C. D.或
【分析】分点B'在线段AB上,点B'在BA延长线上两种情况讨论,根据勾股定理可求MB'的长度.
【解答】解:①如图1中:当点B'在线段AB上,连接OC.
∵AB=10,AB'=6,
∴AO=BO=5=OC,BB'=4,
∴B'O=1,
∵B,B′关于CD对称,
∴BE=B'E=2,
∴OE=OB′+EB′=3,
在Rt△OCE中,CE2=OC2﹣OE2=25﹣9=16,
在Rt△B'CE中,B'C2.
②若点B'在BA的延长线上,连接OC,
∵AB'=6,AB=10,
∴B'B=16,AO=BO=OC=5,
∵B,B′关于CD对称,
∴B'E=BE=8,
∴OE=BE﹣BO=3,
在Rt△CEO,CE2=CO2﹣OE2=25﹣9=16,
在Rt△B'CE中,B'C4,
综上所述B'C=2或4,
故选:B.
【题型5 利用圆周角求最值】
【例5】(2022 瑶海区三模)如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
【分析】根据轴对称的性质得到:点N关于AB的对称点N′,连接MN′交AB于P,此时PM+PN最小,即△PMN周长的最小,利用圆心角、弧、弦的关系以及轴对称的性质进行计算即可.
【解答】解:如图,作点N关于AB的对称点N′,则点N′在⊙O上,连接MN′交AB于P,此时PM+PN最小,即PM+PN=MN′,
∵点N是的中点,∠BAM=20°,
∴,
∴∠BAN′=10°,
∴∠MAN′=20°+10°=30°,
∴∠MON′=60°,
∴△MON′是正三角形,
∴OM=ON′=MN′AB=4,
又∵MN=2,
∴△PMN周长的最小值为2+4=6,
故选:C.
【变式5-1】(2022 陈仓区一模)如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
【分析】如图,由题意当AD⊥BC时,⊙O的半径最小,因为∠EAF=60°,是定值,所以此时EF的值最小.
【解答】解:如图,∵∠ABC=45°,∠ACB=75°,
∴BAC=180°﹣75°﹣45°=60°,
由题意当AD⊥BC时,⊙O的半径最小,
∵∠EAF=60°,是定值,
∴此时EF的值最小,
过OD的中点K作MN⊥AD交⊙O于M、N,连接ON、AN、AM,则△AMN是等边三角形,
在Rt△ABD中,∠ABC=45°,AB=4,
∴AD=BD=2,
∴OK=KD,ON,
在Rt△ONK中,NK=KM,
∴MN,
∴∠EAF=∠MAN=60°,
∴,
∴EF=MN,
∴EF的最小值为,
故答案为:.
【变式5-2】(2022秋 大连期末)如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为的中点,E是直径AB上一动点,则CE+DE最小值为( )
A.1 B. C. D.2
【分析】作点D关于AB的对称点为D′,连接OC,OD,OD′,CD′,交AB于点E,则CE+DE的最小值就是CD′的长度,根据已知易证∠COD′=90°,然后利用勾股定理进行计算即可解答.
【解答】解:作点D关于AB的对称点为D′,连接OC,OD,OD′,CD′,交AB于点E,
∴DE=D′E,
∴CE+DE=CE+D′E=CD′,
∵∠CAB=30°,
∴∠COB=2∠CAB=60°,
∵D为的中点,
∴,
∵,
∴,
∴∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∵AB=2,
∴OC=OD′=1,
∴CD′,
∴CE+DE最小值为:,
故选:B.
【变式5-3】(2022 杏花岭区校级三模)如图,矩形ABCD中,AB,BC=AB2,E为射线BA上一动点,连接CE交以BE为直径的圆于点H,则线段DH长度的最小值为 .
【分析】取BC的中点G,连接BH,HG,DG.解直角三角形求出GH,DG,根据DH≥DG﹣GH即可判断.
【解答】解:取BC的中点G,连接BH,HG,DG.
∵四边形ABCD是矩形,
∴AB=CD,BC=AB2,∠DCG=90°,
∵CG=BG,
∴DG,
∵BE是直径,
∴∠BHE=∠BHC=90°,
∵BG=GC,
∴HGBC,
∵DH≥DG﹣HG,
∴DH,
∴DH的最小值为.
故答案为.
【题型6 圆周角中的证明】
【例6】(2022秋 定陶区期末)如图1.在⊙O中AB=AC,∠ACB=70°,点E在劣弧上运动,连接EC,BE,交AC于点F.
(1)求∠E的度数;
(2)当点E运动到使BE⊥AC时,连接AO并延长,交BE于点D,交BC于点G,交⊙O于点M,依据题意在备用图中画出图形.并证明:G为DM的中点.
【分析】(1)求出∠A=40°,利用圆周角定理解决问题即可;
(2)证明BD=BM,BG⊥DM,利用等腰三角形的三线合一的性质证明即可.
【解答】(1)解:如图1中,∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°﹣2×70°=40°,
∵弧BC=弧BC,
∴∠BEC=∠BAC=40°;
(2)证明:依据题意画图如下:
连接BM,CM.
∵AB=AC,
∴,
又∵,
∴,
∴BM=CM,AM⊥BC,∠BAM=∠CAM=20°,
∴∠MBC=∠CAM=20°,
∵BE⊥AC,AM⊥BC,
∴∠BGD=∠AFD=90°,
∴∠BDG=∠ADF=70°,
∵,
∴∠BMA=∠ACB=70°,
∴∠BMA=∠BDG=70°,
∴BD=BM,
又∵BG⊥DM,
∴GD=GM,即点G为DM的中点.
【变式6-1】(2022春 金山区校级月考)已知CD为⊙O的直径,A、B为⊙O上两点,点C为劣弧AB中点,连接DA、BA、AC,且∠B=30°.
(1)求证:∠D=30°;
(2)F、G分别为线段CD、AC上两点,满足DF=AG,连接AF、OG,取OG中点H,连接CH,请猜测AF与CH之间的数量关系,并证明.
【分析】(1)利用圆周角定理证明即可;
(2)结论:AF=2CH.延长DC到T,使得CT=CO,证明△CGT≌△OFA(SAS),推出AF=GT,再利用三角形中位线定理证明.
【解答】(1)证明:∵∠ABC=30°,
又∵∠D=∠ABC,
∴∠D=30°;
(2)解:结论:AF=2CH.
理由:延长DC到T,使得CT=CO.
∵∠AOC=2∠ABC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠ACO=∠AOC=60°,AC=OA=OC,
∴CT=OC=OA,∠AOF=∠GCT=120°,
∵OA=AC,DF=AG,
∴OF=CG,
在△CGT和△OFA中,
,
∴△CGT≌△OFA(SAS),
∴AF=GT,
∵OH=HG,OC=CT,
∴GT=2CH,
∴AF=2CH.
【变式6-2】(2022 武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE的形状,并证明你的结论;
(2)若AB=10,BE=2,求BC的长.
【分析】(1)由角平分线的定义可知,∠BAE=∠CAD=∠CBD,∠ABE=∠EBC,所以∠BED=∠DBE,所以BD=ED,因为AB为直径,所以∠ADB=90°,所以△BDE是等腰直角三角形.
(2)连接OC、CD、OD,OD交BC于点F.因为∠DBC=∠CAD=∠BAD=∠BCD.所以BD=DC.因为OB=OC.所以OD垂直平分BC.由△BDE是等腰直角三角形,BE=2,可得BD=2.因为OB=OD=5.设OF=t,则DF=5﹣t.在Rt△BOF和Rt△BDF中,52﹣t2=(2)2﹣(5﹣t)2,解出t的值即可.
【解答】解:(1)△BDE为等腰直角三角形.理由如下:
∵AE 平分∠BAC,BE 平分∠ABC,
∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠DBC+∠CBE,
∴∠BED=∠DBE.
∴BD=ED.
∵AB为直径,
∴∠ADB=90°
∴△BDE是等腰直角三角形.
另解:计算∠AEB=135°也可以得证.
(2)解:连接OC、CD、OD,OD交BC于点F.
∵∠DBC=∠CAD=∠BAD=∠BCD.
∴BD=DC.
∵OB=OC.
∴OD垂直平分BC.
∵△BDE是等腰直角三角形,BE=2,
∴BD=2.
∵AB=10,
∴OB=OD=5.
设OF=t,则DF=5﹣t.
在Rt△BOF和Rt△BDF中,52﹣t2=(2)2﹣(5﹣t)2,
解得t=3,
∴BF=4.
∴BC=8.
另解:分别延长AC,BD相交于点G.则△MBG为等腰三角形,先计算AG=10,BG=4,AD=4,再根据面积相等求得BC.
【变式6-3】(2022 南召县四模)阅读下面材料,完成相应的任务:
阿基米德是有史以来最伟大的数学家之一、《阿基米德全集》收集了已发现的阿基米德著作,它对于了解古希腊数学,研究古希腊数学思想以及整个科技史都是十分宝贵的.其中论述了阿基米德折弦定理:从圆周上任一点出发的两条弦,所组成的折线,称之为该圆的一条折弦.一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影,就是折弦的中点.
如图1,AB和BC是⊙O的两条弦(即ABC是圆的一条折弦),BC>AB.M是弧ABC的中点,则从M向BC所作垂线之垂足D是折弦ABC的中点,即CD=AB+BD.
小明认为可以利用“截长法”,如图2:在线段CB上从C点截取一段线段CN=AB,连接MA,MB,MC,MN.
小丽认为可以利用“垂线法”,如图3:过点M作MH⊥AB于点H,连接MA,MB,MC.
任务:(1)请你从小明和小丽的方法中任选一种证明思路,继续书写出证明过程.
(2)就图3证明:MC2﹣MB2=BC AB.
【分析】(1)截长法:首先证明△MBA≌△MNC(SAS),进而得出MB=MN,再利用等腰三角形的性质得出BD=ND,即可得出答案;
垂线法:证明△AHM≌△CDM(AAS),推出MH=DM,AH=CD,再证明Rt△BMH≌△BMD(HL),推出BH=BD,可得结论;
(2)由(1)可知,AC=AM,BH=BD,AH=CD,整理等式即可证得结论.
【解答】(1)截长法:
证明:如图2,在CB上截取CN=AB,连接MA,MB,MC和MN.
∵M是的中点,
∴MA=MC,
在△MBA和△MGC中,
,
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC
∴BD=GD,
∴CD=GC+GD=AB+BD;
垂线法:
证明:如图3,过点M作MH⊥AB于点H,连接MA,MB,MC,
∵M是的中点,
∴AM=CM,
∵MH⊥AH,MD⊥BC,
∴∠H=∠CDM=90°,
∵∠A=∠C,
在△AHM和△CDM中,
,
∴△AHM≌△CDM(AAS),
∴MH=DM,AH=CD,
∵∠H=∠BDM=90°,BM=BM,
∴Rt△BMH≌△BMD(HL),
∴BH=BD,
∴CD=AH=AB+BH=AB+BD;
(2)在Rt△AHM中,AM2=AH2+MH2,
在Rt△BHM中,BM2=BH2+MH2,
由(1)可知,AC=AM,BH=BD,AH=CD,
∴MC2﹣MB2=AM2﹣MB2=AH2+HM2﹣BH
【题型7 圆周角中的多结论问题】
【例7】(2022 兰陵县二模)如图,在⊙O中,AB是⊙O的直径,AB=10,,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】①错误,证明∠EOB=∠BOD=60°即可;
②正确.证明∠CED=30°,可得结论;
③错误,M是动点,DM不一定垂直CE;
④正确,连接EM,证明ME=MD,推出MC+MD=MC+ME≥CE=10,可得结论.
【解答】解:∵,
∴∠AOC=∠COD=∠DOB=60°,
∵E,D关于AB对称,
∴∠EOB=∠BOD=60°,故①错误,
∵∠CED∠COD=30°,
∴∠DOB=2∠CED,故②正确,
∵M是动点,
∴DM不一定垂直CE,故③错误,
连接EM.
则ME=MD,
∴CM+DM=MC+ME≥CE=10,故④正确,
故选:B.
【变式7-1】(2022秋 淅川县期末)如图,已知:点A、B、C、D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
A.2 B.3 C.4 D.5
【分析】根据圆内接四边形的性质、圆周角定理和圆心角、弧、弦之间的关系逐个判断即可.
【解答】解:∵AB=CD,
∴,
∴,
∴∠AOC=∠BOD,故①正确;
∵圆周角∠BAD和圆心角∠BOD都对着,
∴∠BOD=2∠BAD,故②正确;
∵,
∴AC=BD,故③正确;
∵圆周角∠CAB和∠BDC都对着,
∴∠CAB=∠BDC,故④正确;
延长DO交⊙O于M,连接AM,
∵D、C、A、M四点共圆,
∴∠CDO+∠CAM=180°(圆内接四边形对角互补),
∵∠CAM>∠CAO,
∴∠CAO+∠CDO<180°,故⑤错误;
即正确的个数是4个,
故选:C.
【变式7-2】(2022秋 厦门期末)在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D.要使得⊙O与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是 ②④ .(写出所有正确答案的序号)
①∠BAC>60°;②45°<∠ABC<60°;③BDAB;④AB<DEAB.
【分析】结合等腰三角形的性质及圆周角定理对所给条件逐个进行分析判断.
【解答】解:在△ABC中,AB=AC,
①当∠BAC>60°时,若∠BAC=90°时,此时点E与点A重合,不符合题意,故①不满足;
②当∠ABC≤45°时,点E与点A重合,不符合题意,
当∠ABC≥60°时,点E与点O不关于AD对称,
当45°<∠ABC<60°时,点E关于直线AD的对称点在线段OA上,故②满足条件;
③当AB≤BDAB时,点E关于直线AD的对称点在线段OA上,故③不满足条件;
④AB<DEAB时,点E关于直线AD的对称点在线段OA上,故④满足条件;
故答案为:②④.
【变式7-3】(2022秋 东台市月考)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是 ①③④ .(填序号)
【分析】①由直径所对圆周角是直角,
②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
③由平行线得到∠OCB=∠DBC,再由同圆的半径相等得到结论判断出∠OBC=∠DBC;
④用半径垂直于不是直径的弦,必平分弦;
⑤得不到△CEF和△BED中对应相等的边,所以不一定全等.
【解答】解:①∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
故①正确;
②∵∠AEC=∠ABC+∠A,∠AOC=∠ABC+∠C,
根据图形及已知不能推出∠C=∠A,
∴∠AOC≠∠AEC,
故②不正确;
③∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,
故③正确;
④∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥BD,
∴∠AFO=90°,
∵点O为圆心,
∴AF=DF,
故④正确;
⑤∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故⑤不正确;
综上可知:其中一定成立的有①③④,
故答案为:①③④.
【题型8 构造圆利用圆周角解决三角形或四边形中的问题】
【例8】(2022春 杏花岭区校级月考)如图,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴正半轴上,且∠ACB=45°,则点C的坐标为( )
A.(0,7) B.(0,2) C.(0,6) D.(0,3)
【分析】在x轴的上方作等腰直角△ABF,FB=FA,∠BAF=90°,以F为圆心,FA为半径作⊙F交y轴于M,首先证明点C即为点M,根据FC,构建方程即可解决问题.
【解答】解:在x轴的上方作等腰直角△ABF,FB=FA,∠BAF=90°,以F为圆心,FA为半径作⊙F交y轴于M,
∵∠ACB∠AFB=45°,
∴点C即为点M,
∵A(﹣2,0),B(3,0),△ABF是等腰直角三角形,
∴F(,),FA=FB=FC,设C(0,m),
则()2+(m)2=()2,
解得m=6或﹣1(舍弃),
∴C(0,6),
故选:C.
【变式8-1】(2022秋 秦淮区期末)如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= 124 °.
【分析】根据AB=BD=BC得出A、D、C在以B为圆心,以AB为半径的圆上,作圆周角∠AEC,根据圆周角定理得出∠EABC=56°,根据圆内接四边形的性质得出∠ADC+∠E=180°,再求出答案即可.
【解答】解:∵AB=BD=BC,
∴A、D、C在以B为圆心,以AB为半径的圆上,
如图,作圆周角∠AEC,
∵∠ABC=112°,
∴∠EABC=56°,
∵四边形ADCE是⊙B的圆内接四边形,
∴∠ADC+∠E=180°,
∴∠ADC=180°﹣56°=124°,
故答案为:124.
【变式8-2】(2022 北京模拟)已知三角形ABC是锐角三角形,其中∠A=30°,BC=4,设BC边上的高为h,则h的取值范围是 4h≤4+2 .
【分析】做出三角形的外接圆,根据h≤AO+OP求解即可.
【解答】解:如图1,作△ABC的外接圆⊙O,连接OA,OB,OC,过O作OP⊥BC,
∵∠BAC=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∵BC=4,
∴OA=BC=4,PO=2,
∴h≤AO+OP=4+2,
如图2,A1B⊥BC,A2C⊥BC,则A1B=4,
∵三角形ABC是锐角三角形,
∴点A在之间,
∴h的取值范围是:4h≤4+2,
故答案为:4h≤4+2.
【变式8-3】(2022春 西湖区校级月考)已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为 或4或2或2 .
【分析】如图,连接AC,AE,根据已知条件得到△ABC是等边三角形,求得BE=CE=2,AE⊥BC,∠EAC=30°,推出AC是以CE为弦的圆的直径,设圆心为O,当⊙O与CD边交于P1,则∠EP1C=30°,过C作CH⊥P1E于H,解直角三角形得到P1E;当⊙O与AD交于P2,A(P3),由AD∥CE,推出四边形AECP2是矩形,得到P2E=AC=4,P3E=1E=2,当⊙O与AB交于P4,得到△BP4E是等边三角形,求得P4E=BE=2,于是得到结论.
【解答】解:如图,连接AC,AE,
∵AB=BC=4,∠B=60°,
∴△ABC是等边三角形,
∵点E为BC的中点,
∴BE=CE=2,AE⊥BC,∠EAC=30°,
∴AC是以CE为弦的圆的直径,
设圆心为O,
当⊙O与CD边交于P1,则∠EP1C=30°,
∵∠ECP1=105°,
∴∠P1EC=45°,
过C作CH⊥P1E于H,
∴EH=CHCE,
∴P1HHC,
∴P1E;
当⊙O与AD交于P2,A(P3),
∵AD∥CE,
∴∠ECP2=∠AP2C=90°,
∴四边形AECP2是矩形,
∴P2E=AC=4,P3E=P2C=2,
当⊙O与AB交于P4,
∵∠AP4C=90°,∠EP4C=30°,
∴∠BP4E=60°,
∴△BP4E是等边三角形,
∴P4E=BE=2,
综上所述,若∠CPE=30°,则EP的长为或4或2或2,
故答案为:或4或2或2.
【题型9 圆周角与量角器的综合运用】
【例9】(2022 南召县模拟)以O为中心点的量角器与直角三角板ABC按如图方式摆放,量角器的0刻度线与斜边AB重合.点D为斜边AB上一点,作射线CD交弧AB于点E,如果点E所对应的读数为50°,那么∠BDE的大小为( )
A.100° B.110° C.115° D.130°
【分析】由圆周角定理得出∠ACE=25°,进而得出∠BCE=65°,再由外角的性质得出∠BDE=∠BCE+∠CBD,代入计算即可得出答案.
【解答】解:如图,连接OE,
∵点E所对应的读数为50°,
∴∠AOE=50°,
∵AB为直径,∠ACB=90°,
∴点C在⊙O上,
∴∠ACE∠AOE50°=25°,
∴∠BCE=90°﹣25°=65°,
∵∠BDE是△BDC的外角,
∴∠BDE=∠BCE+∠DBC=65°+45°=110°,
故选:B.
【变式9-1】(2022秋 南京期中)将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆圆心上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A= 24° .
【分析】以EF为直径作半圆,延长BO交圆于M,连接OC,根据已知度数求出∠BOA、∠BOF、∠AOB的度数,根据圆周角定理求出∠B,根据三角形内角和定理求出即可.
【解答】解:如图,以EF为直径作半圆,延长BO交圆于M,连接OC,
∵点B,C,D对应的读数分别为160°、72°、50°,
∴∠BOA=160°﹣50°=110°,∠BOF=180°﹣160°=20°,∠COE=72°,
∴∠COM=72°+20°=92°,
∴∠B∠COM=46°,
∴∠A=180°﹣∠B﹣∠AOB=180°﹣110°﹣46°=24°.
故答案为:24°.
【变式9-2】(2022秋 高港区期中)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应的刻度值为50°,则∠BCD的度数为 65° .
【分析】根据圆周角定理分别求出∠ACB、∠ACD,计算即可.
【解答】解:由圆周角定理可知,∠ACD50°=25°,∠ACB=90°,
∴∠BCD=∠ACB﹣∠ACD=65°,
故答案为:65°.
【变式9-3】(2022秋 北京期末)如图,量角器的直径与直角三角尺ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,则第20秒点E在量角器上对应的读数是 120 °.
【分析】首先连接OE,由∠ACB=90°,易得点E,A,B,C共圆,然后由圆周角定理,求得点E在量角器上对应的读数.
【解答】解:
连接OE,
∵∠ACB=90°,AB为半圆的直径,
∴E、A、C、B四点共圆,
∴∠ACP=3°×20=60°,
∴∠AOE=2∠ACP=120°,
即第20秒点E在量角器上对应的读数是120°,
故答案为:120.
【题型10 利用圆周角求取值范围】
【例10】(2022 观山湖区模拟)如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是 60°<β<75° .
【分析】当P点与D点重合是∠DAB=75°,与O重合则OAB=60°,∠OAB<∠PAB<∠DAB,即可得出结果.
【解答】解:连接DA,OA,则△OAB是等边三角形,
∴∠OAB=∠AOB=60°,
∵DC是直径,DC⊥AB,
∴∠AOC∠AOB=30°,
∴∠ADC=15°,
∴∠DAB=75°,
∵∠OAB<∠PAB<∠DAB,
∴60°<β<75°;
故答案为:60°<β<75°.
【变式10-1】(2022 河南三模)如图,点O是以AC为直径的半圆的圆心,点B在上,∠ACB=30°,AC=2.点D是直径AC上一动点(与点A,C不重合),记OD的长为m.连接BD,点A关于BD的对称点为点A′,当点A′落在由直径AC,弦围成的封闭图形内部时(不包含边界),m的取值范围是 0<m .
【分析】直径所对的圆周角是直角,在直角三角形中,30°所对的直角边是斜边的一半,根据点A关于BD的对称点为点A′,得到DA=DA′,考虑点A′进入该区域和离开该区域的两个m的值即可得出答案.
【解答】解:如图,∵AC是半圆的直径,
∴∠ABC=90°,
∵∠ACB=30°,AC=2,
∴AB=1,
∵点A关于BD的对称点为点A′,
∴DA=DA′,
当点D与点O重合时,DA=DA′=r,点A′在上,m=0;
当点D在AO中点时,点A′在直径AC上,m,
∴m的取值范围为:0<m.
故答案为:0<m.
【变式10-2】(2022秋 台州期中)如图,已知AB是⊙O的一条弦,点C是⊙O的优弧ACB上的一个动点(不与A,B不重合),
(1)设∠ACB的平分线与劣弧AB交于点P,试猜想点P劣弧AB上的位置是否会随点C的运动而变化?请说明理由
(2)如图②,设AB=8,⊙O的半径为5,在(1)的条件下,四边形ACBP的面积是否为定值?若是定值,请求出这个定值;若不是定值,请求出ACBP的面积的取值范围.
【分析】(1)点P位置不会随点C的运动而变化,根据角平分线的定义得到∠ACP=∠BCP,于是得到,即P是劣弧AB的中点.即可得到点P位置不会变化.
(2)如图,连接OP,交AB于E,根据垂径定理得到OP⊥AB,AEAB=4.根据勾股定理得到OE3,PE=2.求得S△ABP.于是得到当CP经过圆心O时,如图,C到AB距离最大,即△ABC的AB边上的最大高线是CE=8.求得四边形ACBP的最大面积是40.即可得到结论.
【解答】解:(1)点P位置不会随点C的运动而变化,
理由:如图1,
∵CP平分∠ACB,
∴∠ACP=∠BCP,
∴,
即P是劣弧AB的中点.
∴点P位置不会变化.
(2)∵△ABC的面积不是定值,△ABP的面积为定值
∴四边形ACBP的面积不是定值.
如图,连接OP,交AB于E,
∵,OP是半径.
∴OP⊥AB,AEAB=4.
∵OA=5.
∴OE3,PE=2.
∴S△ABP.
∴当CP经过圆心O时,如图,C到AB距离最大,即△ABC的AB边上的最大高线是CE=8.
∵AB=8,
∴△ABC的最大面积是32.
∴四边形ACBP的最大面积是40.
综上,四边形ACBP的面积不是定值,它的取值范围是8<S四边形ACBP≤40.
【变式10-3】(2022秋 高新区校级期末)如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB是⊙O上关于A、B的滑动角.若⊙O的半径是1,AB,则∠APB的取值范围为 45°≤∠APB≤60°或120°≤∠APB≤135° .
【分析】首先连接OA,OB,AB,先假设AB求出∠APB的度数,同理得出当AB时,∠APB的度数即可.
【解答】解:连接OA,OB,AB,假设AB
∵圆O半径为1,AB,
∴OA2+OB2=AB2,
∴∠AOB=90°,
若点P在优弧AB上,则∠APB∠AOB=45°,
若点P在劣弧AB上,则∠AP′B=180°﹣∠APB=135°.
∴∠APB的度数为45°或135°.
假设AB,
∵圆O半径为1,
∴∠OAB=30°,
∴∠AOB=120°,
∴若点P在优弧AB上,则∠APB∠AOB=60°,
若点P在劣弧AB上,则∠AP′B=180°﹣∠APB=120°.
故∠APB的取值范围为:45°≤∠APB≤60°或120°≤∠APB≤135°.
故答案为:45°≤∠APB≤60°或120°≤∠APB≤135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
圆周角定理10大题型
TOC \o "1-3" \h \u
HYPERLINK \l "_Toc24819" 【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】 2
HYPERLINK \l "_Toc32120" 【题型2 同弧或等弧所对的圆周角相等的运用】 5
HYPERLINK \l "_Toc2689" 【题型3 直径所对的圆周角是90°的运用】 9
HYPERLINK \l "_Toc21132" 【题型4 翻折中的圆周角的运用】 13
HYPERLINK \l "_Toc10283" 【题型5 利用圆周角求最值】 18
HYPERLINK \l "_Toc27772" 【题型6 圆周角中的证明】 22
HYPERLINK \l "_Toc9392" 【题型7 圆周角中的多结论问题】 28
HYPERLINK \l "_Toc11917" 【题型8 构造圆利用圆周角解决三角形或四边形中的问题】 32
HYPERLINK \l "_Toc29627" 【题型9 圆周角与量角器的综合运用】 37
HYPERLINK \l "_Toc19793" 【题型10 利用圆周角求取值范围】 40
【知识点1 圆周角定理及其推论】
圆周角定理 定理:圆周角的度数等于它所对的弧的圆心角度数的一半 是所对的圆心角,是所对的圆周角,
推论1:同弧或等弧所对的圆周角相等 和都是所对的圆周角
推论2:直径所对的圆周角是直角,的圆周角所对的弦是直径 是的直径是所对的圆周角是所对的圆周角 是的直径
【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】
【例1】(2022 鼓楼区校级模拟)如图,CD是⊙O的直径,⊙O上的两点A,B分别在直径CD的两侧,且∠ABC=78°,则∠AOD的度数为( )
A.12° B.22° C.24° D.44°
【变式1-1】(2022 温州)如图,AB,AC是⊙O的两条弦,OD⊥AB于点D,OE⊥AC于点E,连结OB,OC.若∠DOE=130°,则∠BOC的度数为( )
A.95° B.100° C.105° D.130°
【变式1-2】(2022 蓝山县一模)如图,点A,B,C在⊙O上,∠1=40°,∠C=25°,则∠B=( )
A.100° B.70° C.55° D.65°
【变式1-3】(2022春 汉阳区校级月考)如图,AB,CD为⊙O的两条弦,若∠A+∠C=120°,AB=2,CD=4,则⊙O的半径为( )
A.2 B.2 C. D.
【题型2 同弧或等弧所对的圆周角相等的运用】
【例2】(2022 保亭县二模)如图,AB为⊙O的直径,点C、D在圆上,CE⊥AB于点E,若∠D=48°,则∠1=( )
A.42° B.45° C.48° D.52°
【变式2-1】(2022 南充)如图,AB为⊙O的直径,弦CD⊥AB于点E,OF⊥BC于点F,∠BOF=65°,则∠AOD为( )
A.70° B.65° C.50° D.45°
【变式2-2】(2022 十堰二模)如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以BC为直径的⊙O交AB于点D.E是⊙O上一点,且,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
【变式2-3】(2022 本溪模拟)如图,在⊙O中,,直径CD⊥AB于点N,P是上一点,则∠BPD的度数是 .
【题型3 直径所对的圆周角是90°的运用】
【例3】(2022 中山市三模)如图,AB是⊙O的直径,若AC=2,∠D=60°,则BC长等于( )
A.4 B.5 C. D.
【变式3-1】(2022 潍坊二模)如图,已知以△ABC的边AB为直径的⊙O经过点C,OD⊥AC交⊙O于点D,连接BD.若∠BAC=36°,则∠ODB的度数为( )
A.32° B.27° C.24° D.18°
【变式3-2】(2022 江夏区校级开学)如图,⊙O的直径AB为8,D为上的一点,DE⊥AC于点E,若CE=3AE,∠BAC=30°,则DE的长是( )
A. B.2 C. D.
【变式3-3】(2022秋 如皋市校级期中)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
【题型4 翻折中的圆周角的运用】
【例4】(2022春 福田区校级月考)如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若,则∠BCD的度数是( )
A.22.5° B.30° C.45° D.60°
【变式4-1】(2022秋 萧山区期中)如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D,连结CD,若∠BAC=25°,则∠BDC的度数为( )
A.45° B.55° C.65° D.70°
【变式4-2】(2022秋 硚口区期末)如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=( )
A.110° B.112.5° C.115° D.117.5°
【变式4-3】(2022秋 丹江口市期中)已知⊙O的直径AB长为10,弦CD⊥AB,将⊙O沿CD翻折,翻折后点B的对应点为点B′,若AB′=6,CB′的长为( )
A. B.或 C. D.或
【题型5 利用圆周角求最值】
【例5】(2022 瑶海区三模)如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
【变式5-1】(2022 陈仓区一模)如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
【变式5-2】(2022秋 大连期末)如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为的中点,E是直径AB上一动点,则CE+DE最小值为( )
A.1 B. C. D.2
【变式5-3】(2022 杏花岭区校级三模)如图,矩形ABCD中,AB,BC=AB2,E为射线BA上一动点,连接CE交以BE为直径的圆于点H,则线段DH长度的最小值为 .
【题型6 圆周角中的证明】
【例6】(2022秋 定陶区期末)如图1.在⊙O中AB=AC,∠ACB=70°,点E在劣弧上运动,连接EC,BE,交AC于点F.
(1)求∠E的度数;
(2)当点E运动到使BE⊥AC时,连接AO并延长,交BE于点D,交BC于点G,交⊙O于点M,依据题意在备用图中画出图形.并证明:G为DM的中点.
【变式6-1】(2022春 金山区校级月考)已知CD为⊙O的直径,A、B为⊙O上两点,点C为劣弧AB中点,连接DA、BA、AC,且∠B=30°.
(1)求证:∠D=30°;
(2)F、G分别为线段CD、AC上两点,满足DF=AG,连接AF、OG,取OG中点H,连接CH,请猜测AF与CH之间的数量关系,并证明.
【变式6-2】(2022 武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE的形状,并证明你的结论;
(2)若AB=10,BE=2,求BC的长.
【变式6-3】(2022 南召县四模)阅读下面材料,完成相应的任务:
阿基米德是有史以来最伟大的数学家之一、《阿基米德全集》收集了已发现的阿基米德著作,它对于了解古希腊数学,研究古希腊数学思想以及整个科技史都是十分宝贵的.其中论述了阿基米德折弦定理:从圆周上任一点出发的两条弦,所组成的折线,称之为该圆的一条折弦.一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影,就是折弦的中点.
如图1,AB和BC是⊙O的两条弦(即ABC是圆的一条折弦),BC>AB.M是弧ABC的中点,则从M向BC所作垂线之垂足D是折弦ABC的中点,即CD=AB+BD.
小明认为可以利用“截长法”,如图2:在线段CB上从C点截取一段线段CN=AB,连接MA,MB,MC,MN.
小丽认为可以利用“垂线法”,如图3:过点M作MH⊥AB于点H,连接MA,MB,MC.
任务:(1)请你从小明和小丽的方法中任选一种证明思路,继续书写出证明过程.
(2)就图3证明:MC2﹣MB2=BC AB.
【题型7 圆周角中的多结论问题】
【例7】(2022 兰陵县二模)如图,在⊙O中,AB是⊙O的直径,AB=10,,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
【变式7-1】(2022秋 淅川县期末)如图,已知:点A、B、C、D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
A.2 B.3 C.4 D.5
【变式7-2】(2022秋 厦门期末)在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D.要使得⊙O与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是 .(写出所有正确答案的序号)
①∠BAC>60°;②45°<∠ABC<60°;③BDAB;④AB<DEAB.
【变式7-3】(2022秋 东台市月考)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是 .(填序号)
【题型8 构造圆利用圆周角解决三角形或四边形中的问题】
【例8】(2022春 杏花岭区校级月考)如图,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴正半轴上,且∠ACB=45°,则点C的坐标为( )
A.(0,7) B.(0,2) C.(0,6) D.(0,3)
【变式8-1】(2022秋 秦淮区期末)如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= °.
【变式8-2】(2022 北京模拟)已知三角形ABC是锐角三角形,其中∠A=30°,BC=4,设BC边上的高为h,则h的取值范围是 .
【变式8-3】(2022春 西湖区校级月考)已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为 .
【题型9 圆周角与量角器的综合运用】
【例9】(2022 南召县模拟)以O为中心点的量角器与直角三角板ABC按如图方式摆放,量角器的0刻度线与斜边AB重合.点D为斜边AB上一点,作射线CD交弧AB于点E,如果点E所对应的读数为50°,那么∠BDE的大小为( )
A.100° B.110° C.115° D.130°
【变式9-1】(2022秋 南京期中)将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆圆心上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A= .
【变式9-2】(2022秋 高港区期中)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应的刻度值为50°,则∠BCD的度数为 .
【变式9-3】(2022秋 北京期末)如图,量角器的直径与直角三角尺ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,则第20秒点E在量角器上对应的读数是 °.
【题型10 利用圆周角求取值范围】
【例10】(2022 观山湖区模拟)如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是 .
【变式10-1】(2022 河南三模)如图,点O是以AC为直径的半圆的圆心,点B在上,∠ACB=30°,AC=2.点D是直径AC上一动点(与点A,C不重合),记OD的长为m.连接BD,点A关于BD的对称点为点A′,当点A′落在由直径AC,弦围成的封闭图形内部时(不包含边界),m的取值范围是 .
【变式10-2】(2022秋 台州期中)如图,已知AB是⊙O的一条弦,点C是⊙O的优弧ACB上的一个动点(不与A,B不重合),
(1)设∠ACB的平分线与劣弧AB交于点P,试猜想点P劣弧AB上的位置是否会随点C的运动而变化?请说明理由
(2)如图②,设AB=8,⊙O的半径为5,在(1)的条件下,四边形ACBP的面积是否为定值?若是定值,请求出这个定值;若不是定值,请求出ACBP的面积的取值范围.
【变式10-3】(2022秋 高新区校级期末)如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB是⊙O上关于A、B的滑动角.若⊙O的半径是1,AB,则∠APB的取值范围为 .
圆周角定理【十大题型】
TOC \o "1-3" \h \u
HYPERLINK \l "_Toc24819" 【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】 2
HYPERLINK \l "_Toc32120" 【题型2 同弧或等弧所对的圆周角相等的运用】 5
HYPERLINK \l "_Toc2689" 【题型3 直径所对的圆周角是90°的运用】 9
HYPERLINK \l "_Toc21132" 【题型4 翻折中的圆周角的运用】 13
HYPERLINK \l "_Toc10283" 【题型5 利用圆周角求最值】 18
HYPERLINK \l "_Toc27772" 【题型6 圆周角中的证明】 22
HYPERLINK \l "_Toc9392" 【题型7 圆周角中的多结论问题】 28
HYPERLINK \l "_Toc11917" 【题型8 构造圆利用圆周角解决三角形或四边形中的问题】 32
HYPERLINK \l "_Toc29627" 【题型9 圆周角与量角器的综合运用】 37
HYPERLINK \l "_Toc19793" 【题型10 利用圆周角求取值范围】 40
【知识点1 圆周角定理及其推论】
圆周角定理 定理:圆周角的度数等于它所对的弧的圆心角度数的一半 是所对的圆心角,是所对的圆周角,
推论1:同弧或等弧所对的圆周角相等 和都是所对的圆周角
推论2:直径所对的圆周角是直角,的圆周角所对的弦是直径 是的直径是所对的圆周角是所对的圆周角 是的直径
【题型1 圆周角的度数等于它所对弧上的圆心角的一半的运用】
【例1】(2022 鼓楼区校级模拟)如图,CD是⊙O的直径,⊙O上的两点A,B分别在直径CD的两侧,且∠ABC=78°,则∠AOD的度数为( )
A.12° B.22° C.24° D.44°
【分析】利用圆周角定理求出∠AOC=156°,可得结论.
【解答】解:∵∠AOC=2∠ABC,∠ABC=78°,
∴∠AOC=156°,
∴∠AOD=180°﹣∠AOC=24°,
故选:C.
【变式1-1】(2022 温州)如图,AB,AC是⊙O的两条弦,OD⊥AB于点D,OE⊥AC于点E,连结OB,OC.若∠DOE=130°,则∠BOC的度数为( )
A.95° B.100° C.105° D.130°
【分析】根据四边形的内角和等于360°计算可得∠BAC=50°,再根据圆周角定理得到∠BOC=2∠BAC,进而可以得到答案.
【解答】解:∵OD⊥AB,OE⊥AC,
∴∠ADO=90°,∠AEO=90°,
∵∠DOE=130°,
∴∠BAC=360°﹣90°﹣90°﹣130°=50°,
∴∠BOC=2∠BAC=100°,
故选:B.
【变式1-2】(2022 蓝山县一模)如图,点A,B,C在⊙O上,∠1=40°,∠C=25°,则∠B=( )
A.100° B.70° C.55° D.65°
【分析】根据圆周角定理得出∠BOC=2∠1=80°,根据三角形内角和定理得出∠1+∠B+∠ADB=180°,∠C+∠BOC+∠ODC=180°,求出∠1+∠B=∠BOC+∠C即可.
【解答】解:设OB交AC于D,
∵∠1=40°,
∴∠BOC=2∠1=80°,
∵∠1+∠B+∠ADB=180°,∠C+∠BOC+∠ODC=180°,∠ADB=∠ODC,
∴∠1+∠B=∠BOC+∠C,
∵∠C=25°,
∴40°+∠B=80°+25°,
∴∠B=65°,
故选:D.
【变式1-3】(2022春 汉阳区校级月考)如图,AB,CD为⊙O的两条弦,若∠A+∠C=120°,AB=2,CD=4,则⊙O的半径为( )
A.2 B.2 C. D.
【分析】连接OB,OA,OC,OD,证明∠AOB+∠COD=90°,在⊙O上点D的右侧取一点E,使得DE=AB,过点E作ET⊥CD交CD的延长线于点T,则,利用勾股定理求解即可.
【解答】解:如图,连接OB,OA,OC,OD,
∵∠BOC=2∠CAB,∠AOD=2∠ACD,∠CAB+∠ACD=120°,
∴∠BOC+∠AOD=240°,
∴∠AOB+∠COD=120°,
在⊙O上点D的右侧取一点E,使得DE=AB,过点E作ET⊥CD交CD的延长线于点T,则,
∴∠AOB=∠DOE,
∴∠COE=120°,
∴∠CDE=120°,
∴∠EDT=60°,
∵DE=AB=2,
∴DT=1,ET,
∴CT=CD+DT=4+1=5,
∴CE,
作OF⊥CE,则∠COF=60°,CF,
∴OC=OE,
故选:D.
【题型2 同弧或等弧所对的圆周角相等的运用】
【例2】(2022 保亭县二模)如图,AB为⊙O的直径,点C、D在圆上,CE⊥AB于点E,若∠D=48°,则∠1=( )
A.42° B.45° C.48° D.52°
【分析】连接AC,根据圆周角定理得出∠A=∠D=48°,∠ACB=90°,求出∠ABC,根据垂直求出∠CEB,再求出∠1即可.
【解答】解:连接AC,
由圆周角定理得:∠A=∠D,
∵∠D=48°,
∴∠A=48°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC=90°﹣∠A=42°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠1=90°﹣∠ABC=48°,
故选:C.
【变式2-1】(2022 南充)如图,AB为⊙O的直径,弦CD⊥AB于点E,OF⊥BC于点F,∠BOF=65°,则∠AOD为( )
A.70° B.65° C.50° D.45°
【分析】先根据三角形的内角和定理可得∠B=25°,由垂径定理得:,最后由圆周角定理可得结论.
【解答】解:∵OF⊥BC,
∴∠BFO=90°,
∵∠BOF=65°,
∴∠B=90°﹣65°=25°,
∵弦CD⊥AB,AB为⊙O的直径,
∴,
∴∠AOD=2∠B=50°.
故选:C.
【变式2-2】(2022 十堰二模)如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以BC为直径的⊙O交AB于点D.E是⊙O上一点,且,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
【分析】连接OD,根据圆心角、弧、弦之间的关系得出∠DOC=∠EOC,根据直角三角形的两锐角互余得出∠B=90°﹣∠A=36°,根据圆周角定理求出∠DOC=2∠B=72°,求出∠EOC=∠DOC=72°,再根据四边形的内角和等于360°求出即可.
【解答】解:解法一、连接OD,
∵,
∴∠DOC=∠EOC,
∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∴∠DOC=2∠B=72°,
∴∠EOC=∠DOC=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
解法二、∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∵,
∴∠COE=2∠B=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
故选:B.
【变式2-3】(2022 本溪模拟)如图,在⊙O中,,直径CD⊥AB于点N,P是上一点,则∠BPD的度数是 30° .
【分析】连接OA、OB,如图,先根据垂径定理得到,所以,利用圆心角、弧、弦的关系得到∠AOC=∠BOC=∠AOB=120°,所以∠BOD=60°,然后根据圆周角定理求解.
【解答】解:连接OA、OB,如图,
∵CD⊥AB,
∴,
∵,
∴,
∴∠AOC=∠BOC=∠AOB360°=120°,
∴∠BOD=180°﹣120°=60°,
∴∠BPD∠BOD=30°.
故答案为:30°.
【题型3 直径所对的圆周角是90°的运用】
【例3】(2022 中山市三模)如图,AB是⊙O的直径,若AC=2,∠D=60°,则BC长等于( )
A.4 B.5 C. D.
【分析】根据圆周角定理得出∠ACB=90°,∠CAB=∠D=60°,求出∠ABC=90°﹣∠CAB=30°,根据含30度角的直角三角形的性质求出AB=2AC=4,再根据勾股定理求出BC即可.
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠D=60°,
∴∠CAB=∠D=60°,
∴∠ABC=90°﹣∠CAB=30°,
∵AC=2,
∴AB=2AC=4,
∴BC2,
故选:D.
【变式3-1】(2022 潍坊二模)如图,已知以△ABC的边AB为直径的⊙O经过点C,OD⊥AC交⊙O于点D,连接BD.若∠BAC=36°,则∠ODB的度数为( )
A.32° B.27° C.24° D.18°
【分析】设AC与OD相交于点E,根据直径所对的圆周角是直角可得∠ACB=90°,从而求出∠ABC=54°,再根据垂直定义可得∠AEO=90°,从而可得OD∥BC,然后利用等腰三角形和平行线的性质可得BD平分∠ABC,即可解答.
【解答】解:设AC与OD相交于点E,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=36°,
∴∠ABC=90°﹣∠BAC=54°,
∵OD⊥AC,
∴∠AEO=90°,
∴∠AEO=∠ACB=90°,
∴OD∥BC,
∴∠ODB=∠DBC,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠OBD=∠DBC∠ABC=27°,
∴∠ODB=∠OBD=27°,
故选:B.
【变式3-2】(2022 江夏区校级开学)如图,⊙O的直径AB为8,D为上的一点,DE⊥AC于点E,若CE=3AE,∠BAC=30°,则DE的长是( )
A. B.2 C. D.
【分析】在30°的直角三角形ABC中求出AC=4,根据CE=3AE得到AE,再分别求出DF、ME、MF的长度即可得解.
【解答】解:如图,连接连接BC、OD,作OF⊥DE,交DE的延长线于点F,DF、AB交于点M
∵AB为直径,
∴∠ACB=90°,
又∵∠BAC=30°,
∴BC=4,AC=4,
∵CE=3AE,
∴AE,
∵DE⊥AC,∠BAC=30°,
∴EM=1,AM=2,
∴OM=OA﹣AM=4﹣2=2,
在Rt△OMF中,
∵∠OFM=90°,∠OMF=∠AME=90°﹣30°=60°,OM=2,
∴MF=1,OF,
∵∠F=90°,
∴DF,
∴DE=DF﹣ME﹣MF.
故选:B.
【变式3-3】(2022秋 如皋市校级期中)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
【分析】(1)过点O作OE⊥AC于E,由垂径定理可知AEAC2=1,根据翻折后点D与圆心O重合,可知OEr,在Rt△AOE中,根据勾股定理可得出r的值;
(2)连接BC,根据直径所对的圆周角是直角求出∠ACB,根据直角三角形两锐角互余求出∠B,再根据翻折的性质得到所对的圆周角,然后根据∠ACD等于所对的圆周角减去所对的圆周角,计算即可得解.
【解答】解:(1)如图1,过点O作OE⊥AC于E
则AEAC2=1,
∵翻折后点D与圆心O重合,
∴OEr,
在Rt△AOE中,AO2=AE2+OE2,
即r2=12+(r)2,解得r;
(2)连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质,所对的圆周角为∠B,所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.
【题型4 翻折中的圆周角的运用】
【例4】(2022春 福田区校级月考)如图,AB是⊙O的直径,BC是⊙O的弦,先将沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若,则∠BCD的度数是( )
A.22.5° B.30° C.45° D.60°
【分析】证明∠CAB=3α,利用三角形内角和定理求出α,可得结论.
【解答】解:设∠ABC=α,
则,,的度数都为2α,
∴的度数=4α,
∵翻折,
∴的度数=4α,
∴的度数=2α+4α=6α,
∵的度数的度数=180°,
∴2α+6α=180°,
∴α=22.5°.
∴的度数=90°
∴∠BCD=45°.
故选:C.
【变式4-1】(2022秋 萧山区期中)如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点D,连结CD,若∠BAC=25°,则∠BDC的度数为( )
A.45° B.55° C.65° D.70°
【分析】解法一、补齐翻折后的弧为圆⊙P,根据圆周角定理得出,求出∠BDC=∠DBC,根据圆周角定理求出∠ACB=90°,再求出∠ABC即可;解法二、过D作DE⊥AC于E,延长DE交⊙O于F,连接AF、CF、BC,根据圆周角定理得出∠ACB=90°,根据翻折变换得出∠FAC=∠BAC=25°,∠DCA=∠FCA,根据圆内接四边形的性质得出∠BAF+∠BCF=180°,求出∠ACF=40°,求出∠ACD=∠ACF=40°,再根据三角形的外角性质求出即可.
【解答】解:解法一、补齐翻折后的弧为圆⊙P
则⊙O和⊙P为等圆,
∵∠BAC在⊙O和⊙P中分别对应弧BC和弧DC,
∴(在同圆或等圆中,相等的圆周角所对的弧相等),
∴BC=DC,
∴∠BDC=∠DBC,
∵AB为⊙O直径,
∴∠DBC=90°﹣∠BAC=65°,
∴∠BDC=65°;
解法二、过D作DE⊥AC于E,延长DE交⊙O于F,连接AF、CF、BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵将劣弧AC沿弦AC翻折交AB于点D,连结CD,∠BAC=25°,
∴∠FAC=∠BAC=25°,∠DCA=∠FCA,
∵点A、F、C、B四点共圆,
∴∠BAF+∠BCF=180°,
∴25°+25°+90°+∠ACF=180°,
解得:∠ACF=40°,
即∠ACD=∠ACF=40°,
∵∠BAC=25°,
∴∠BDC=∠BAC+∠ACD=25°+40°=65°,
故选:C.
【变式4-2】(2022秋 硚口区期末)如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=( )
A.110° B.112.5° C.115° D.117.5°
【分析】如图,连接OA,OB,BD.设∠DAB=x.用x表示出∠BDC,∠BCD,∠DBC,利用三角形内角和定理,构建方程求解.
【解答】解:如图,连接OA,OB,BD.设∠DAB=x.
∵,
∴DA=DB,
∵,
∴BD=CD,
∴∠DAB=∠DBA=x,∠BDC=∠BCD=∠DAB+∠ABD=2x,
∵OC∥AB,
∴∠OCA=∠DAB=x,
∵OA=OC=OB,
∴∠OCB=∠OBC=3x,∠OAD=∠OCA=x,∠OAB=∠OBA=2x,
∴∠OBD=x,
∴∠CBD=4x,
在△BDC中,∠BDC+∠DCB+∠DBC=180°,
∴2x+2x+4x=180°,
∴x=22.5°,
∴∠ABC=5x=112.5°,
故选:B.
【变式4-3】(2022秋 丹江口市期中)已知⊙O的直径AB长为10,弦CD⊥AB,将⊙O沿CD翻折,翻折后点B的对应点为点B′,若AB′=6,CB′的长为( )
A. B.或 C. D.或
【分析】分点B'在线段AB上,点B'在BA延长线上两种情况讨论,根据勾股定理可求MB'的长度.
【解答】解:①如图1中:当点B'在线段AB上,连接OC.
∵AB=10,AB'=6,
∴AO=BO=5=OC,BB'=4,
∴B'O=1,
∵B,B′关于CD对称,
∴BE=B'E=2,
∴OE=OB′+EB′=3,
在Rt△OCE中,CE2=OC2﹣OE2=25﹣9=16,
在Rt△B'CE中,B'C2.
②若点B'在BA的延长线上,连接OC,
∵AB'=6,AB=10,
∴B'B=16,AO=BO=OC=5,
∵B,B′关于CD对称,
∴B'E=BE=8,
∴OE=BE﹣BO=3,
在Rt△CEO,CE2=CO2﹣OE2=25﹣9=16,
在Rt△B'CE中,B'C4,
综上所述B'C=2或4,
故选:B.
【题型5 利用圆周角求最值】
【例5】(2022 瑶海区三模)如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=2,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
【分析】根据轴对称的性质得到:点N关于AB的对称点N′,连接MN′交AB于P,此时PM+PN最小,即△PMN周长的最小,利用圆心角、弧、弦的关系以及轴对称的性质进行计算即可.
【解答】解:如图,作点N关于AB的对称点N′,则点N′在⊙O上,连接MN′交AB于P,此时PM+PN最小,即PM+PN=MN′,
∵点N是的中点,∠BAM=20°,
∴,
∴∠BAN′=10°,
∴∠MAN′=20°+10°=30°,
∴∠MON′=60°,
∴△MON′是正三角形,
∴OM=ON′=MN′AB=4,
又∵MN=2,
∴△PMN周长的最小值为2+4=6,
故选:C.
【变式5-1】(2022 陈仓区一模)如图,△ABC中,∠ABC=45°,∠ACB=75°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O,分别交AB、AC于点E、F,连接EF,则线段EF长度的最小值为 .
【分析】如图,由题意当AD⊥BC时,⊙O的半径最小,因为∠EAF=60°,是定值,所以此时EF的值最小.
【解答】解:如图,∵∠ABC=45°,∠ACB=75°,
∴BAC=180°﹣75°﹣45°=60°,
由题意当AD⊥BC时,⊙O的半径最小,
∵∠EAF=60°,是定值,
∴此时EF的值最小,
过OD的中点K作MN⊥AD交⊙O于M、N,连接ON、AN、AM,则△AMN是等边三角形,
在Rt△ABD中,∠ABC=45°,AB=4,
∴AD=BD=2,
∴OK=KD,ON,
在Rt△ONK中,NK=KM,
∴MN,
∴∠EAF=∠MAN=60°,
∴,
∴EF=MN,
∴EF的最小值为,
故答案为:.
【变式5-2】(2022秋 大连期末)如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为的中点,E是直径AB上一动点,则CE+DE最小值为( )
A.1 B. C. D.2
【分析】作点D关于AB的对称点为D′,连接OC,OD,OD′,CD′,交AB于点E,则CE+DE的最小值就是CD′的长度,根据已知易证∠COD′=90°,然后利用勾股定理进行计算即可解答.
【解答】解:作点D关于AB的对称点为D′,连接OC,OD,OD′,CD′,交AB于点E,
∴DE=D′E,
∴CE+DE=CE+D′E=CD′,
∵∠CAB=30°,
∴∠COB=2∠CAB=60°,
∵D为的中点,
∴,
∵,
∴,
∴∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∵AB=2,
∴OC=OD′=1,
∴CD′,
∴CE+DE最小值为:,
故选:B.
【变式5-3】(2022 杏花岭区校级三模)如图,矩形ABCD中,AB,BC=AB2,E为射线BA上一动点,连接CE交以BE为直径的圆于点H,则线段DH长度的最小值为 .
【分析】取BC的中点G,连接BH,HG,DG.解直角三角形求出GH,DG,根据DH≥DG﹣GH即可判断.
【解答】解:取BC的中点G,连接BH,HG,DG.
∵四边形ABCD是矩形,
∴AB=CD,BC=AB2,∠DCG=90°,
∵CG=BG,
∴DG,
∵BE是直径,
∴∠BHE=∠BHC=90°,
∵BG=GC,
∴HGBC,
∵DH≥DG﹣HG,
∴DH,
∴DH的最小值为.
故答案为.
【题型6 圆周角中的证明】
【例6】(2022秋 定陶区期末)如图1.在⊙O中AB=AC,∠ACB=70°,点E在劣弧上运动,连接EC,BE,交AC于点F.
(1)求∠E的度数;
(2)当点E运动到使BE⊥AC时,连接AO并延长,交BE于点D,交BC于点G,交⊙O于点M,依据题意在备用图中画出图形.并证明:G为DM的中点.
【分析】(1)求出∠A=40°,利用圆周角定理解决问题即可;
(2)证明BD=BM,BG⊥DM,利用等腰三角形的三线合一的性质证明即可.
【解答】(1)解:如图1中,∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°﹣2×70°=40°,
∵弧BC=弧BC,
∴∠BEC=∠BAC=40°;
(2)证明:依据题意画图如下:
连接BM,CM.
∵AB=AC,
∴,
又∵,
∴,
∴BM=CM,AM⊥BC,∠BAM=∠CAM=20°,
∴∠MBC=∠CAM=20°,
∵BE⊥AC,AM⊥BC,
∴∠BGD=∠AFD=90°,
∴∠BDG=∠ADF=70°,
∵,
∴∠BMA=∠ACB=70°,
∴∠BMA=∠BDG=70°,
∴BD=BM,
又∵BG⊥DM,
∴GD=GM,即点G为DM的中点.
【变式6-1】(2022春 金山区校级月考)已知CD为⊙O的直径,A、B为⊙O上两点,点C为劣弧AB中点,连接DA、BA、AC,且∠B=30°.
(1)求证:∠D=30°;
(2)F、G分别为线段CD、AC上两点,满足DF=AG,连接AF、OG,取OG中点H,连接CH,请猜测AF与CH之间的数量关系,并证明.
【分析】(1)利用圆周角定理证明即可;
(2)结论:AF=2CH.延长DC到T,使得CT=CO,证明△CGT≌△OFA(SAS),推出AF=GT,再利用三角形中位线定理证明.
【解答】(1)证明:∵∠ABC=30°,
又∵∠D=∠ABC,
∴∠D=30°;
(2)解:结论:AF=2CH.
理由:延长DC到T,使得CT=CO.
∵∠AOC=2∠ABC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠ACO=∠AOC=60°,AC=OA=OC,
∴CT=OC=OA,∠AOF=∠GCT=120°,
∵OA=AC,DF=AG,
∴OF=CG,
在△CGT和△OFA中,
,
∴△CGT≌△OFA(SAS),
∴AF=GT,
∵OH=HG,OC=CT,
∴GT=2CH,
∴AF=2CH.
【变式6-2】(2022 武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE的形状,并证明你的结论;
(2)若AB=10,BE=2,求BC的长.
【分析】(1)由角平分线的定义可知,∠BAE=∠CAD=∠CBD,∠ABE=∠EBC,所以∠BED=∠DBE,所以BD=ED,因为AB为直径,所以∠ADB=90°,所以△BDE是等腰直角三角形.
(2)连接OC、CD、OD,OD交BC于点F.因为∠DBC=∠CAD=∠BAD=∠BCD.所以BD=DC.因为OB=OC.所以OD垂直平分BC.由△BDE是等腰直角三角形,BE=2,可得BD=2.因为OB=OD=5.设OF=t,则DF=5﹣t.在Rt△BOF和Rt△BDF中,52﹣t2=(2)2﹣(5﹣t)2,解出t的值即可.
【解答】解:(1)△BDE为等腰直角三角形.理由如下:
∵AE 平分∠BAC,BE 平分∠ABC,
∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠DBC+∠CBE,
∴∠BED=∠DBE.
∴BD=ED.
∵AB为直径,
∴∠ADB=90°
∴△BDE是等腰直角三角形.
另解:计算∠AEB=135°也可以得证.
(2)解:连接OC、CD、OD,OD交BC于点F.
∵∠DBC=∠CAD=∠BAD=∠BCD.
∴BD=DC.
∵OB=OC.
∴OD垂直平分BC.
∵△BDE是等腰直角三角形,BE=2,
∴BD=2.
∵AB=10,
∴OB=OD=5.
设OF=t,则DF=5﹣t.
在Rt△BOF和Rt△BDF中,52﹣t2=(2)2﹣(5﹣t)2,
解得t=3,
∴BF=4.
∴BC=8.
另解:分别延长AC,BD相交于点G.则△MBG为等腰三角形,先计算AG=10,BG=4,AD=4,再根据面积相等求得BC.
【变式6-3】(2022 南召县四模)阅读下面材料,完成相应的任务:
阿基米德是有史以来最伟大的数学家之一、《阿基米德全集》收集了已发现的阿基米德著作,它对于了解古希腊数学,研究古希腊数学思想以及整个科技史都是十分宝贵的.其中论述了阿基米德折弦定理:从圆周上任一点出发的两条弦,所组成的折线,称之为该圆的一条折弦.一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影,就是折弦的中点.
如图1,AB和BC是⊙O的两条弦(即ABC是圆的一条折弦),BC>AB.M是弧ABC的中点,则从M向BC所作垂线之垂足D是折弦ABC的中点,即CD=AB+BD.
小明认为可以利用“截长法”,如图2:在线段CB上从C点截取一段线段CN=AB,连接MA,MB,MC,MN.
小丽认为可以利用“垂线法”,如图3:过点M作MH⊥AB于点H,连接MA,MB,MC.
任务:(1)请你从小明和小丽的方法中任选一种证明思路,继续书写出证明过程.
(2)就图3证明:MC2﹣MB2=BC AB.
【分析】(1)截长法:首先证明△MBA≌△MNC(SAS),进而得出MB=MN,再利用等腰三角形的性质得出BD=ND,即可得出答案;
垂线法:证明△AHM≌△CDM(AAS),推出MH=DM,AH=CD,再证明Rt△BMH≌△BMD(HL),推出BH=BD,可得结论;
(2)由(1)可知,AC=AM,BH=BD,AH=CD,整理等式即可证得结论.
【解答】(1)截长法:
证明:如图2,在CB上截取CN=AB,连接MA,MB,MC和MN.
∵M是的中点,
∴MA=MC,
在△MBA和△MGC中,
,
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC
∴BD=GD,
∴CD=GC+GD=AB+BD;
垂线法:
证明:如图3,过点M作MH⊥AB于点H,连接MA,MB,MC,
∵M是的中点,
∴AM=CM,
∵MH⊥AH,MD⊥BC,
∴∠H=∠CDM=90°,
∵∠A=∠C,
在△AHM和△CDM中,
,
∴△AHM≌△CDM(AAS),
∴MH=DM,AH=CD,
∵∠H=∠BDM=90°,BM=BM,
∴Rt△BMH≌△BMD(HL),
∴BH=BD,
∴CD=AH=AB+BH=AB+BD;
(2)在Rt△AHM中,AM2=AH2+MH2,
在Rt△BHM中,BM2=BH2+MH2,
由(1)可知,AC=AM,BH=BD,AH=CD,
∴MC2﹣MB2=AM2﹣MB2=AH2+HM2﹣BH
【题型7 圆周角中的多结论问题】
【例7】(2022 兰陵县二模)如图,在⊙O中,AB是⊙O的直径,AB=10,,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:
①∠BOE=30°;②∠DOB=2∠CED;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】①错误,证明∠EOB=∠BOD=60°即可;
②正确.证明∠CED=30°,可得结论;
③错误,M是动点,DM不一定垂直CE;
④正确,连接EM,证明ME=MD,推出MC+MD=MC+ME≥CE=10,可得结论.
【解答】解:∵,
∴∠AOC=∠COD=∠DOB=60°,
∵E,D关于AB对称,
∴∠EOB=∠BOD=60°,故①错误,
∵∠CED∠COD=30°,
∴∠DOB=2∠CED,故②正确,
∵M是动点,
∴DM不一定垂直CE,故③错误,
连接EM.
则ME=MD,
∴CM+DM=MC+ME≥CE=10,故④正确,
故选:B.
【变式7-1】(2022秋 淅川县期末)如图,已知:点A、B、C、D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
A.2 B.3 C.4 D.5
【分析】根据圆内接四边形的性质、圆周角定理和圆心角、弧、弦之间的关系逐个判断即可.
【解答】解:∵AB=CD,
∴,
∴,
∴∠AOC=∠BOD,故①正确;
∵圆周角∠BAD和圆心角∠BOD都对着,
∴∠BOD=2∠BAD,故②正确;
∵,
∴AC=BD,故③正确;
∵圆周角∠CAB和∠BDC都对着,
∴∠CAB=∠BDC,故④正确;
延长DO交⊙O于M,连接AM,
∵D、C、A、M四点共圆,
∴∠CDO+∠CAM=180°(圆内接四边形对角互补),
∵∠CAM>∠CAO,
∴∠CAO+∠CDO<180°,故⑤错误;
即正确的个数是4个,
故选:C.
【变式7-2】(2022秋 厦门期末)在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D.要使得⊙O与AC边的交点E关于直线AD的对称点在线段OA上(不与端点重合),需满足的条件可以是 ②④ .(写出所有正确答案的序号)
①∠BAC>60°;②45°<∠ABC<60°;③BDAB;④AB<DEAB.
【分析】结合等腰三角形的性质及圆周角定理对所给条件逐个进行分析判断.
【解答】解:在△ABC中,AB=AC,
①当∠BAC>60°时,若∠BAC=90°时,此时点E与点A重合,不符合题意,故①不满足;
②当∠ABC≤45°时,点E与点A重合,不符合题意,
当∠ABC≥60°时,点E与点O不关于AD对称,
当45°<∠ABC<60°时,点E关于直线AD的对称点在线段OA上,故②满足条件;
③当AB≤BDAB时,点E关于直线AD的对称点在线段OA上,故③不满足条件;
④AB<DEAB时,点E关于直线AD的对称点在线段OA上,故④满足条件;
故答案为:②④.
【变式7-3】(2022秋 东台市月考)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是 ①③④ .(填序号)
【分析】①由直径所对圆周角是直角,
②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
③由平行线得到∠OCB=∠DBC,再由同圆的半径相等得到结论判断出∠OBC=∠DBC;
④用半径垂直于不是直径的弦,必平分弦;
⑤得不到△CEF和△BED中对应相等的边,所以不一定全等.
【解答】解:①∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
故①正确;
②∵∠AEC=∠ABC+∠A,∠AOC=∠ABC+∠C,
根据图形及已知不能推出∠C=∠A,
∴∠AOC≠∠AEC,
故②不正确;
③∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,
故③正确;
④∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥BD,
∴∠AFO=90°,
∵点O为圆心,
∴AF=DF,
故④正确;
⑤∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故⑤不正确;
综上可知:其中一定成立的有①③④,
故答案为:①③④.
【题型8 构造圆利用圆周角解决三角形或四边形中的问题】
【例8】(2022春 杏花岭区校级月考)如图,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴正半轴上,且∠ACB=45°,则点C的坐标为( )
A.(0,7) B.(0,2) C.(0,6) D.(0,3)
【分析】在x轴的上方作等腰直角△ABF,FB=FA,∠BAF=90°,以F为圆心,FA为半径作⊙F交y轴于M,首先证明点C即为点M,根据FC,构建方程即可解决问题.
【解答】解:在x轴的上方作等腰直角△ABF,FB=FA,∠BAF=90°,以F为圆心,FA为半径作⊙F交y轴于M,
∵∠ACB∠AFB=45°,
∴点C即为点M,
∵A(﹣2,0),B(3,0),△ABF是等腰直角三角形,
∴F(,),FA=FB=FC,设C(0,m),
则()2+(m)2=()2,
解得m=6或﹣1(舍弃),
∴C(0,6),
故选:C.
【变式8-1】(2022秋 秦淮区期末)如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= 124 °.
【分析】根据AB=BD=BC得出A、D、C在以B为圆心,以AB为半径的圆上,作圆周角∠AEC,根据圆周角定理得出∠EABC=56°,根据圆内接四边形的性质得出∠ADC+∠E=180°,再求出答案即可.
【解答】解:∵AB=BD=BC,
∴A、D、C在以B为圆心,以AB为半径的圆上,
如图,作圆周角∠AEC,
∵∠ABC=112°,
∴∠EABC=56°,
∵四边形ADCE是⊙B的圆内接四边形,
∴∠ADC+∠E=180°,
∴∠ADC=180°﹣56°=124°,
故答案为:124.
【变式8-2】(2022 北京模拟)已知三角形ABC是锐角三角形,其中∠A=30°,BC=4,设BC边上的高为h,则h的取值范围是 4h≤4+2 .
【分析】做出三角形的外接圆,根据h≤AO+OP求解即可.
【解答】解:如图1,作△ABC的外接圆⊙O,连接OA,OB,OC,过O作OP⊥BC,
∵∠BAC=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∵BC=4,
∴OA=BC=4,PO=2,
∴h≤AO+OP=4+2,
如图2,A1B⊥BC,A2C⊥BC,则A1B=4,
∵三角形ABC是锐角三角形,
∴点A在之间,
∴h的取值范围是:4h≤4+2,
故答案为:4h≤4+2.
【变式8-3】(2022春 西湖区校级月考)已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为 或4或2或2 .
【分析】如图,连接AC,AE,根据已知条件得到△ABC是等边三角形,求得BE=CE=2,AE⊥BC,∠EAC=30°,推出AC是以CE为弦的圆的直径,设圆心为O,当⊙O与CD边交于P1,则∠EP1C=30°,过C作CH⊥P1E于H,解直角三角形得到P1E;当⊙O与AD交于P2,A(P3),由AD∥CE,推出四边形AECP2是矩形,得到P2E=AC=4,P3E=1E=2,当⊙O与AB交于P4,得到△BP4E是等边三角形,求得P4E=BE=2,于是得到结论.
【解答】解:如图,连接AC,AE,
∵AB=BC=4,∠B=60°,
∴△ABC是等边三角形,
∵点E为BC的中点,
∴BE=CE=2,AE⊥BC,∠EAC=30°,
∴AC是以CE为弦的圆的直径,
设圆心为O,
当⊙O与CD边交于P1,则∠EP1C=30°,
∵∠ECP1=105°,
∴∠P1EC=45°,
过C作CH⊥P1E于H,
∴EH=CHCE,
∴P1HHC,
∴P1E;
当⊙O与AD交于P2,A(P3),
∵AD∥CE,
∴∠ECP2=∠AP2C=90°,
∴四边形AECP2是矩形,
∴P2E=AC=4,P3E=P2C=2,
当⊙O与AB交于P4,
∵∠AP4C=90°,∠EP4C=30°,
∴∠BP4E=60°,
∴△BP4E是等边三角形,
∴P4E=BE=2,
综上所述,若∠CPE=30°,则EP的长为或4或2或2,
故答案为:或4或2或2.
【题型9 圆周角与量角器的综合运用】
【例9】(2022 南召县模拟)以O为中心点的量角器与直角三角板ABC按如图方式摆放,量角器的0刻度线与斜边AB重合.点D为斜边AB上一点,作射线CD交弧AB于点E,如果点E所对应的读数为50°,那么∠BDE的大小为( )
A.100° B.110° C.115° D.130°
【分析】由圆周角定理得出∠ACE=25°,进而得出∠BCE=65°,再由外角的性质得出∠BDE=∠BCE+∠CBD,代入计算即可得出答案.
【解答】解:如图,连接OE,
∵点E所对应的读数为50°,
∴∠AOE=50°,
∵AB为直径,∠ACB=90°,
∴点C在⊙O上,
∴∠ACE∠AOE50°=25°,
∴∠BCE=90°﹣25°=65°,
∵∠BDE是△BDC的外角,
∴∠BDE=∠BCE+∠DBC=65°+45°=110°,
故选:B.
【变式9-1】(2022秋 南京期中)将量角器按如图所示的方式放置在三角形纸片上,使点O在半圆圆心上,点B在半圆上,边AB,AO分别交半圆于点C,D,点B,C,D对应的读数分别为160°、72°、50°,则∠A= 24° .
【分析】以EF为直径作半圆,延长BO交圆于M,连接OC,根据已知度数求出∠BOA、∠BOF、∠AOB的度数,根据圆周角定理求出∠B,根据三角形内角和定理求出即可.
【解答】解:如图,以EF为直径作半圆,延长BO交圆于M,连接OC,
∵点B,C,D对应的读数分别为160°、72°、50°,
∴∠BOA=160°﹣50°=110°,∠BOF=180°﹣160°=20°,∠COE=72°,
∴∠COM=72°+20°=92°,
∴∠B∠COM=46°,
∴∠A=180°﹣∠B﹣∠AOB=180°﹣110°﹣46°=24°.
故答案为:24°.
【变式9-2】(2022秋 高港区期中)如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应的刻度值为50°,则∠BCD的度数为 65° .
【分析】根据圆周角定理分别求出∠ACB、∠ACD,计算即可.
【解答】解:由圆周角定理可知,∠ACD50°=25°,∠ACB=90°,
∴∠BCD=∠ACB﹣∠ACD=65°,
故答案为:65°.
【变式9-3】(2022秋 北京期末)如图,量角器的直径与直角三角尺ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转,CP与量角器的半圆弧交于点E,则第20秒点E在量角器上对应的读数是 120 °.
【分析】首先连接OE,由∠ACB=90°,易得点E,A,B,C共圆,然后由圆周角定理,求得点E在量角器上对应的读数.
【解答】解:
连接OE,
∵∠ACB=90°,AB为半圆的直径,
∴E、A、C、B四点共圆,
∴∠ACP=3°×20=60°,
∴∠AOE=2∠ACP=120°,
即第20秒点E在量角器上对应的读数是120°,
故答案为:120.
【题型10 利用圆周角求取值范围】
【例10】(2022 观山湖区模拟)如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是 60°<β<75° .
【分析】当P点与D点重合是∠DAB=75°,与O重合则OAB=60°,∠OAB<∠PAB<∠DAB,即可得出结果.
【解答】解:连接DA,OA,则△OAB是等边三角形,
∴∠OAB=∠AOB=60°,
∵DC是直径,DC⊥AB,
∴∠AOC∠AOB=30°,
∴∠ADC=15°,
∴∠DAB=75°,
∵∠OAB<∠PAB<∠DAB,
∴60°<β<75°;
故答案为:60°<β<75°.
【变式10-1】(2022 河南三模)如图,点O是以AC为直径的半圆的圆心,点B在上,∠ACB=30°,AC=2.点D是直径AC上一动点(与点A,C不重合),记OD的长为m.连接BD,点A关于BD的对称点为点A′,当点A′落在由直径AC,弦围成的封闭图形内部时(不包含边界),m的取值范围是 0<m .
【分析】直径所对的圆周角是直角,在直角三角形中,30°所对的直角边是斜边的一半,根据点A关于BD的对称点为点A′,得到DA=DA′,考虑点A′进入该区域和离开该区域的两个m的值即可得出答案.
【解答】解:如图,∵AC是半圆的直径,
∴∠ABC=90°,
∵∠ACB=30°,AC=2,
∴AB=1,
∵点A关于BD的对称点为点A′,
∴DA=DA′,
当点D与点O重合时,DA=DA′=r,点A′在上,m=0;
当点D在AO中点时,点A′在直径AC上,m,
∴m的取值范围为:0<m.
故答案为:0<m.
【变式10-2】(2022秋 台州期中)如图,已知AB是⊙O的一条弦,点C是⊙O的优弧ACB上的一个动点(不与A,B不重合),
(1)设∠ACB的平分线与劣弧AB交于点P,试猜想点P劣弧AB上的位置是否会随点C的运动而变化?请说明理由
(2)如图②,设AB=8,⊙O的半径为5,在(1)的条件下,四边形ACBP的面积是否为定值?若是定值,请求出这个定值;若不是定值,请求出ACBP的面积的取值范围.
【分析】(1)点P位置不会随点C的运动而变化,根据角平分线的定义得到∠ACP=∠BCP,于是得到,即P是劣弧AB的中点.即可得到点P位置不会变化.
(2)如图,连接OP,交AB于E,根据垂径定理得到OP⊥AB,AEAB=4.根据勾股定理得到OE3,PE=2.求得S△ABP.于是得到当CP经过圆心O时,如图,C到AB距离最大,即△ABC的AB边上的最大高线是CE=8.求得四边形ACBP的最大面积是40.即可得到结论.
【解答】解:(1)点P位置不会随点C的运动而变化,
理由:如图1,
∵CP平分∠ACB,
∴∠ACP=∠BCP,
∴,
即P是劣弧AB的中点.
∴点P位置不会变化.
(2)∵△ABC的面积不是定值,△ABP的面积为定值
∴四边形ACBP的面积不是定值.
如图,连接OP,交AB于E,
∵,OP是半径.
∴OP⊥AB,AEAB=4.
∵OA=5.
∴OE3,PE=2.
∴S△ABP.
∴当CP经过圆心O时,如图,C到AB距离最大,即△ABC的AB边上的最大高线是CE=8.
∵AB=8,
∴△ABC的最大面积是32.
∴四边形ACBP的最大面积是40.
综上,四边形ACBP的面积不是定值,它的取值范围是8<S四边形ACBP≤40.
【变式10-3】(2022秋 高新区校级期末)如图,A、B为⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合),我们称∠APB是⊙O上关于A、B的滑动角.若⊙O的半径是1,AB,则∠APB的取值范围为 45°≤∠APB≤60°或120°≤∠APB≤135° .
【分析】首先连接OA,OB,AB,先假设AB求出∠APB的度数,同理得出当AB时,∠APB的度数即可.
【解答】解:连接OA,OB,AB,假设AB
∵圆O半径为1,AB,
∴OA2+OB2=AB2,
∴∠AOB=90°,
若点P在优弧AB上,则∠APB∠AOB=45°,
若点P在劣弧AB上,则∠AP′B=180°﹣∠APB=135°.
∴∠APB的度数为45°或135°.
假设AB,
∵圆O半径为1,
∴∠OAB=30°,
∴∠AOB=120°,
∴若点P在优弧AB上,则∠APB∠AOB=60°,
若点P在劣弧AB上,则∠AP′B=180°﹣∠APB=120°.
故∠APB的取值范围为:45°≤∠APB≤60°或120°≤∠APB≤135°.
故答案为:45°≤∠APB≤60°或120°≤∠APB≤135°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
