浙教版数学九年级上册4.3相似三角形 同步训练(含解析)
文档属性
| 名称 | 浙教版数学九年级上册4.3相似三角形 同步训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 491.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-20 07:28:41 | ||
图片预览



文档简介
4.3相似三角形同步训练——浙教版数学九年级上册
一、选择题
1.如图,已知△ABC∽△DEF,若∠A=35°,∠B=65°,则∠F的度数是( )
A.30° B.35° C.80° D.100°
2.的三边长分别为2,3,4,另有一个与它相似的三角形,其最长边为16,则的周长是( )
A.54 B.36 C.27 D.21
3.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A. B. C. D.
4.若△ABC∽△DEF,且△ABC与△DEF的面积比是,则△ABC与△DEF的对应高的比为( )
A. B. C. D.
5.如图,在等边三角形中,点,分别在,边上,如果∽,,,那么的周长等于( )
A. B. C. D.
6.已知与相似,又,,那么不可能是( )
A.40° B.60° C.80° D.100°
7.如图,已知,若,,,则AC的长是( )
A.12 B.13 C.14 D.15
8.如图△ABC∽△ACD,则下列式子中不成立的是( )
A. = B. =
C.AC2=AD AB D. =
9.如图,已知: , , , 的度数为( )
A. B. C. D.
10.内接于,,延长线交于,若与相似,则( ).
A. B. C. D.
11.如图,在纸板中,,,,是上一点,沿过点的直线剪下一个与相似的小三角形纸板.针对的不同取值,三人的说法如下.下列判断正确的是( )
甲:若,则有种不同的剪法;
乙:若,则有种不同的剪法;
丙:若,则有种不同的剪法.
A.乙错,丙对 B.甲和乙都错 C.乙对,丙错 D.甲错,丙对
二、填空题
12.若D为中边上一点,且EDBC交于E,,若与的相似比为,则 .
13.要把一根1m长的铜丝截成两段,用它们围成两个相似三角形,且相似比为 ,那么截成的两段铜丝的长度差应是 m.
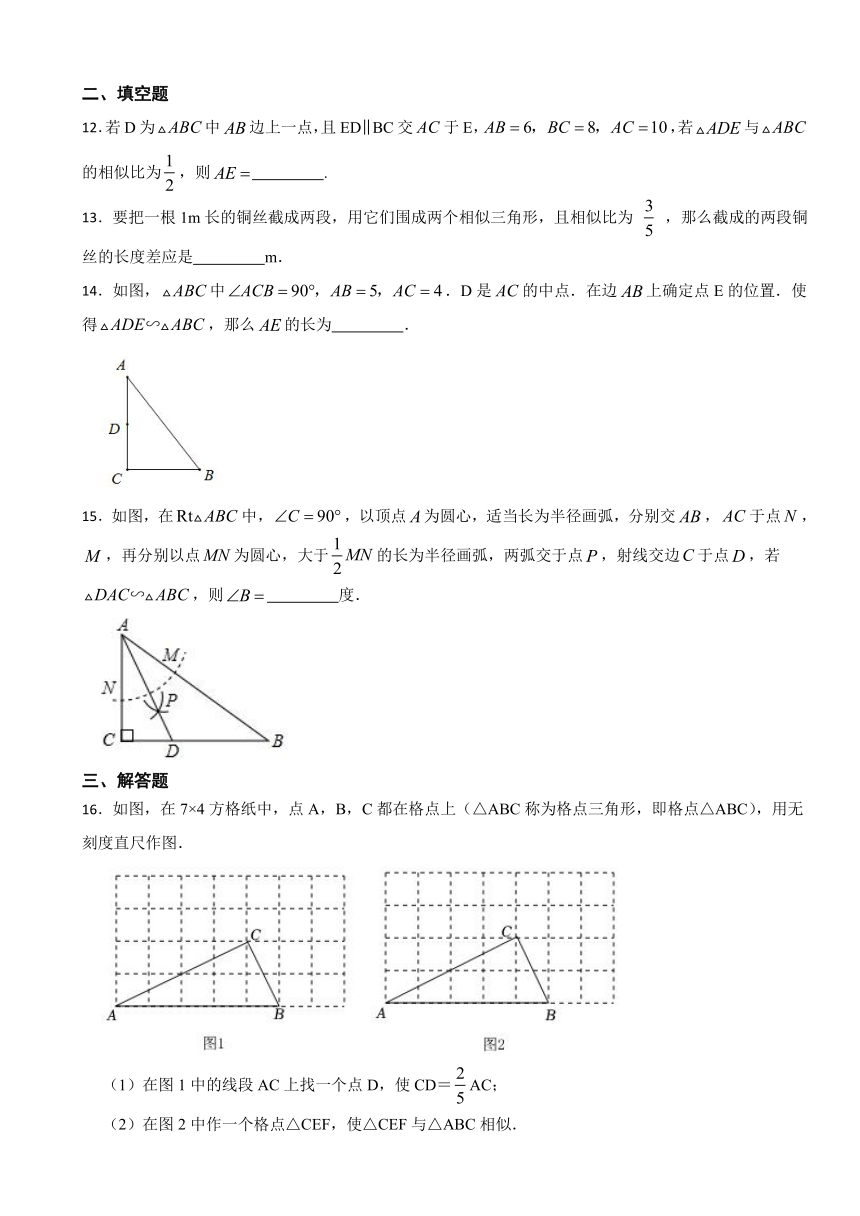
14.如图,中.D是的中点.在边上确定点E的位置.使得,那么的长为 .
15.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以点为圆心,大于的长为半径画弧,两弧交于点,射线交边于点,若,则 度.
三、解答题
16.如图,在7×4方格纸中,点A,B,C都在格点上(△ABC称为格点三角形,即格点△ABC),用无刻度直尺作图.
(1)在图1中的线段AC上找一个点D,使CD=AC;
(2)在图2中作一个格点△CEF,使△CEF与△ABC相似.
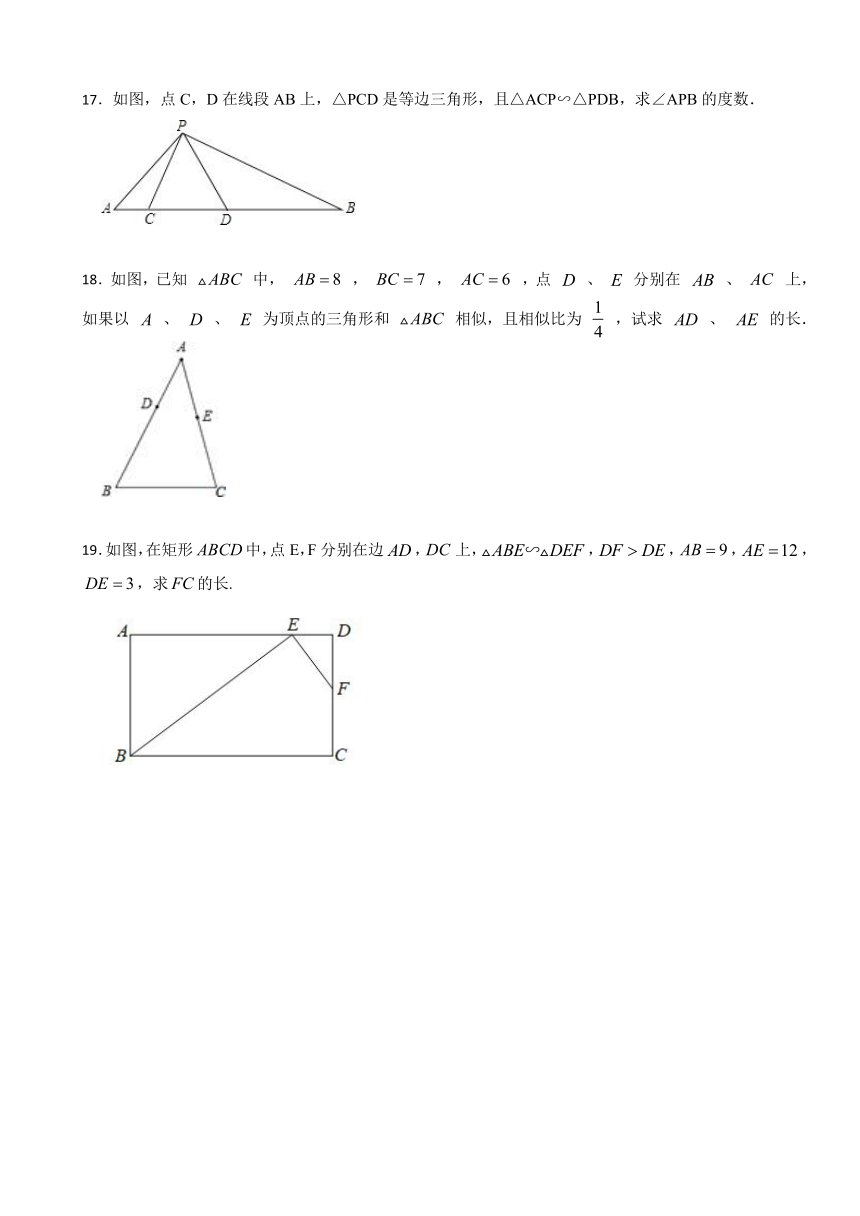
17.如图,点C,D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
18.如图,已知 中, , , ,点 、 分别在 、 上,如果以 、 、 为顶点的三角形和 相似,且相似比为 ,试求 、 的长.
19.如图,在矩形中,点E,F分别在边,上,,,,,,求的长.
答案解析部分
1.【答案】C
【解析】解:∵△ABC中,∠A=35°,∠B=65°,
∴∠C=180°-∠A-∠B=180°-35°-65°=80°,
又∵△ABC∽△DEF,
∴∠F=∠C=80°,
故答案为:C.
2.【答案】B
【解析】解:∵△ABC∽△DEF
∴相似比为:,
△ABC的周长为:,
∴△DEF的周长为:,
故答案为:B.
3.【答案】C
【解析】解:∵由图可知,AB=AC=6,∠B=75°,
∴∠C=75°,∠A=30°,
A、三角形各角的度数分别为75°,52.5°,52.5°,
B、三角形各角的度数都是60°,
C、三角形各角的度数分别为75°,30°,75°,
D、三角形各角的度数分别为40°,70°,70°,
∴只有C选项中三角形各角的度数与题干中三角形各角的度数相等,利用AAA可以判断两个三角形相似.
故答案为:C.
4.【答案】D
【解析】解:∵△ABC∽△DEF,△ABC与△DEF的面积比是,
∴△ABC与△DEF的相似比为,
∴△ABC与△DEF对应高的比为,
故答案为:D.
5.【答案】C
【解析】解:∵△ADE∽△ABC,AD:AB=1:4
∴其周长比为1:4,
∵BC=8cm,三角形ABC为等边三角形
∴△ABC的周长为:24cm
∴的周长等于
答案为:C.
6.【答案】D
【解析】解:∵中,,
∴∠C=180°-∠A-∠B=80°
∵与相似
∴∠D=∠A=40°或∠D=∠B=60°或∠D=∠C=80°
∴不可能是100°
故答案为:D.
7.【答案】A
【解析】解:∵△ADE∽△ACB,
∴,
∴,
故答案为:A.
8.【答案】D
【解析】解:∵△ABC∽△ACD,
∴ = , = , ,
∴AC2=AD AB,
∴A、B、C成立,不符合题意;
D错误,符合题意.
故答案为:D.
9.【答案】D
【解析】解: △ABC∽△DAC
∴∠DAC=∠B=36°,∠BAC=∠D=117°
∠BAD=∠DAC+∠BAC=36°+117°=153°.
故答案为:D
10.【答案】C
【解析】解:如图,连接,设.
∵与相似
∴
∵
∴
又∵
∴
∴
∴
故答案为:C.
11.【答案】C
【解析】解:如下图,过点P作PE∥AB交AC于E,或者过P作PD∥AC交AB与D,
∴,
∴此时
如下图,过P作交AB于F,
∴
此时
如下图,过P作交AC于G,
∴
当G与A重合时,即,
得,
此时
当时,有四种剪法,当时,有3种剪法,
∴甲和乙对,丙错,
故答案为:C.
12.【答案】5
【解析】解:∵ED∥BC,△ADE与△ABC的相似比为,
∴,
∵,
∴.
故答案为:5.
13.【答案】 .
【解析】根据题意知:一段长为 ,另一段长为
所以:两段铜丝的长度差应是 .
14.【答案】
【解析】解:∵△ADE∽△ABC,
∴,
∵D是AC的中点,AC=4,
∴,
∴,
∴,
故答案为:.
15.【答案】30
【解析】解:由作图可知,AD平分∠CAB,
∴∠CAD=∠DAB,
∵△DAC∽△ABC,
∴∠CAD=∠B,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为:30.
16.【答案】(1)解:如图1,点D即为所求;
(2)解:如图2,△CEF即为所求.
17.【答案】解:∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠ACP=120°,
∵△ACP∽△PDB,
∴∠APC=∠B,又∠A=∠A,
∴△ACP∽△ABP,
∴∠APB=∠ACP=120°
18.【答案】解:当 时,相似比为 ,
,
即: ,
解得: , ;
当 时,
,
即: ,
解得: ,
19.【答案】解:∵,
∴,
∵,,,
∴,
解得:,
∵四边形是矩形,
∴,
∴.
即的长度为5.
一、选择题
1.如图,已知△ABC∽△DEF,若∠A=35°,∠B=65°,则∠F的度数是( )
A.30° B.35° C.80° D.100°
2.的三边长分别为2,3,4,另有一个与它相似的三角形,其最长边为16,则的周长是( )
A.54 B.36 C.27 D.21
3.已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A. B. C. D.
4.若△ABC∽△DEF,且△ABC与△DEF的面积比是,则△ABC与△DEF的对应高的比为( )
A. B. C. D.
5.如图,在等边三角形中,点,分别在,边上,如果∽,,,那么的周长等于( )
A. B. C. D.
6.已知与相似,又,,那么不可能是( )
A.40° B.60° C.80° D.100°
7.如图,已知,若,,,则AC的长是( )
A.12 B.13 C.14 D.15
8.如图△ABC∽△ACD,则下列式子中不成立的是( )
A. = B. =
C.AC2=AD AB D. =
9.如图,已知: , , , 的度数为( )
A. B. C. D.
10.内接于,,延长线交于,若与相似,则( ).
A. B. C. D.
11.如图,在纸板中,,,,是上一点,沿过点的直线剪下一个与相似的小三角形纸板.针对的不同取值,三人的说法如下.下列判断正确的是( )
甲:若,则有种不同的剪法;
乙:若,则有种不同的剪法;
丙:若,则有种不同的剪法.
A.乙错,丙对 B.甲和乙都错 C.乙对,丙错 D.甲错,丙对
二、填空题
12.若D为中边上一点,且EDBC交于E,,若与的相似比为,则 .
13.要把一根1m长的铜丝截成两段,用它们围成两个相似三角形,且相似比为 ,那么截成的两段铜丝的长度差应是 m.
14.如图,中.D是的中点.在边上确定点E的位置.使得,那么的长为 .
15.如图,在中,,以顶点为圆心,适当长为半径画弧,分别交,于点,,再分别以点为圆心,大于的长为半径画弧,两弧交于点,射线交边于点,若,则 度.
三、解答题
16.如图,在7×4方格纸中,点A,B,C都在格点上(△ABC称为格点三角形,即格点△ABC),用无刻度直尺作图.
(1)在图1中的线段AC上找一个点D,使CD=AC;
(2)在图2中作一个格点△CEF,使△CEF与△ABC相似.
17.如图,点C,D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
18.如图,已知 中, , , ,点 、 分别在 、 上,如果以 、 、 为顶点的三角形和 相似,且相似比为 ,试求 、 的长.
19.如图,在矩形中,点E,F分别在边,上,,,,,,求的长.
答案解析部分
1.【答案】C
【解析】解:∵△ABC中,∠A=35°,∠B=65°,
∴∠C=180°-∠A-∠B=180°-35°-65°=80°,
又∵△ABC∽△DEF,
∴∠F=∠C=80°,
故答案为:C.
2.【答案】B
【解析】解:∵△ABC∽△DEF
∴相似比为:,
△ABC的周长为:,
∴△DEF的周长为:,
故答案为:B.
3.【答案】C
【解析】解:∵由图可知,AB=AC=6,∠B=75°,
∴∠C=75°,∠A=30°,
A、三角形各角的度数分别为75°,52.5°,52.5°,
B、三角形各角的度数都是60°,
C、三角形各角的度数分别为75°,30°,75°,
D、三角形各角的度数分别为40°,70°,70°,
∴只有C选项中三角形各角的度数与题干中三角形各角的度数相等,利用AAA可以判断两个三角形相似.
故答案为:C.
4.【答案】D
【解析】解:∵△ABC∽△DEF,△ABC与△DEF的面积比是,
∴△ABC与△DEF的相似比为,
∴△ABC与△DEF对应高的比为,
故答案为:D.
5.【答案】C
【解析】解:∵△ADE∽△ABC,AD:AB=1:4
∴其周长比为1:4,
∵BC=8cm,三角形ABC为等边三角形
∴△ABC的周长为:24cm
∴的周长等于
答案为:C.
6.【答案】D
【解析】解:∵中,,
∴∠C=180°-∠A-∠B=80°
∵与相似
∴∠D=∠A=40°或∠D=∠B=60°或∠D=∠C=80°
∴不可能是100°
故答案为:D.
7.【答案】A
【解析】解:∵△ADE∽△ACB,
∴,
∴,
故答案为:A.
8.【答案】D
【解析】解:∵△ABC∽△ACD,
∴ = , = , ,
∴AC2=AD AB,
∴A、B、C成立,不符合题意;
D错误,符合题意.
故答案为:D.
9.【答案】D
【解析】解: △ABC∽△DAC
∴∠DAC=∠B=36°,∠BAC=∠D=117°
∠BAD=∠DAC+∠BAC=36°+117°=153°.
故答案为:D
10.【答案】C
【解析】解:如图,连接,设.
∵与相似
∴
∵
∴
又∵
∴
∴
∴
故答案为:C.
11.【答案】C
【解析】解:如下图,过点P作PE∥AB交AC于E,或者过P作PD∥AC交AB与D,
∴,
∴此时
如下图,过P作交AB于F,
∴
此时
如下图,过P作交AC于G,
∴
当G与A重合时,即,
得,
此时
当时,有四种剪法,当时,有3种剪法,
∴甲和乙对,丙错,
故答案为:C.
12.【答案】5
【解析】解:∵ED∥BC,△ADE与△ABC的相似比为,
∴,
∵,
∴.
故答案为:5.
13.【答案】 .
【解析】根据题意知:一段长为 ,另一段长为
所以:两段铜丝的长度差应是 .
14.【答案】
【解析】解:∵△ADE∽△ABC,
∴,
∵D是AC的中点,AC=4,
∴,
∴,
∴,
故答案为:.
15.【答案】30
【解析】解:由作图可知,AD平分∠CAB,
∴∠CAD=∠DAB,
∵△DAC∽△ABC,
∴∠CAD=∠B,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为:30.
16.【答案】(1)解:如图1,点D即为所求;
(2)解:如图2,△CEF即为所求.
17.【答案】解:∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠ACP=120°,
∵△ACP∽△PDB,
∴∠APC=∠B,又∠A=∠A,
∴△ACP∽△ABP,
∴∠APB=∠ACP=120°
18.【答案】解:当 时,相似比为 ,
,
即: ,
解得: , ;
当 时,
,
即: ,
解得: ,
19.【答案】解:∵,
∴,
∵,,,
∴,
解得:,
∵四边形是矩形,
∴,
∴.
即的长度为5.
同课章节目录
