浙教八年级下册数学第五章第1节《矩形的性质与判定》复习课件(共29张PPT)
文档属性
| 名称 | 浙教八年级下册数学第五章第1节《矩形的性质与判定》复习课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 385.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-12 11:27:21 | ||
图片预览





文档简介
(共29张PPT)
A
B
E
C
D
F
G
中
1、定义:
有一个角是 的 叫矩形。
2、性质和判定:
性 质 判 定
边
角
对角线
同平行四边形
平行四边形
直角
四个角都是直角
对角线相等且互相平分
3、对角线相等的平行四边形.
2、有三个角是直角的四边形.
1、有一个角是直角的平行四边形.
A
B
C
D
∟
∟
∟
∟
O
中
3、直角三角形的性质及判定方法:
角:
直角三角形两锐角互余。
线段:
边角关系:
1、勾股定理:两直角边的平方和等于斜边
的平方。
2、斜边中线的性质:直角三角形斜边中线
等于斜边的一半。
1、直角三角形中,30°角所对的直角边
等于斜边的一半。
2、直角三角形中,若直角边等于斜边的一半,
那么这条直角边所对的角等于30°。
A
B
C
D
中
1、已知矩形的一条对角线与一边的夹角
是40°,则两条对角线所成的锐角的
度数是( )
A、100° B、90° C、80° D、70°
2、矩形的一边长为6,各边中点围成的四
边形的周长是20 ,则矩形的对角线长
为 ,面积为 。
3、平行四边形四个内角的平分线,如果能围成
一个四边形,那么这个四边形一定是( )
A、矩形 B、菱形
C、正方形 D、等腰梯形
4、如图,矩形ABCD中,O是对角线的交点,
若AE⊥BD于E,且
OE∶OD=1∶2,
AE= cm,
则∠AOD = ,
DE= cm。
5、已知:如图,在 ABCD 中,E、F分别为边
AB、CD的中点,BD是对角线,AG∥DB交CB的
延长线于G.
(1)求证:DE=BF;
(2)若四边形 BEDF是
菱形,则四边形
AGBD是什么特殊
四边形?并证明
你的结论.
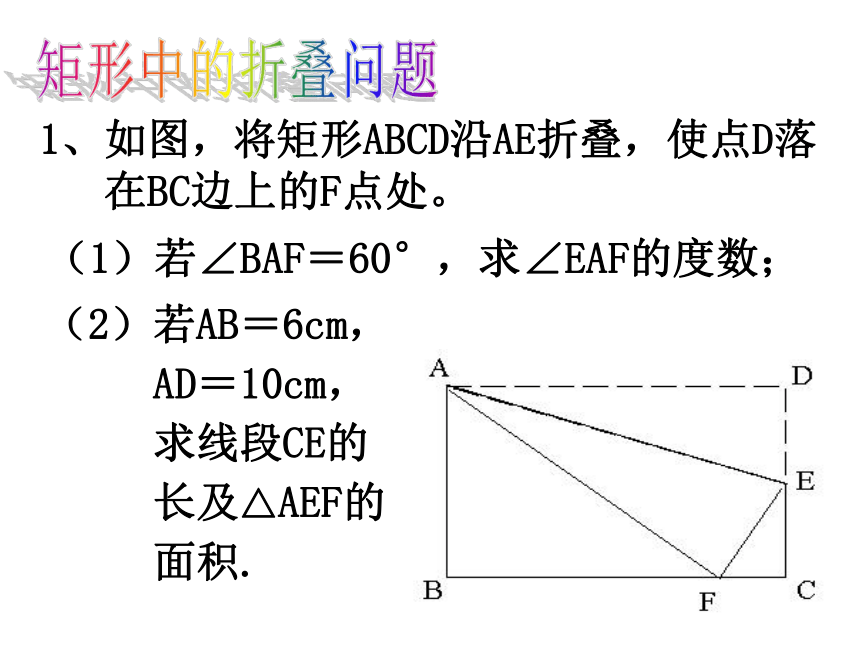
1、如图,将矩形ABCD沿AE折叠,使点D落
在BC边上的F点处。
(1)若∠BAF=60°,求∠EAF的度数;
(2)若AB=6cm,
AD=10cm,
求线段CE的
长及△AEF的
面积.
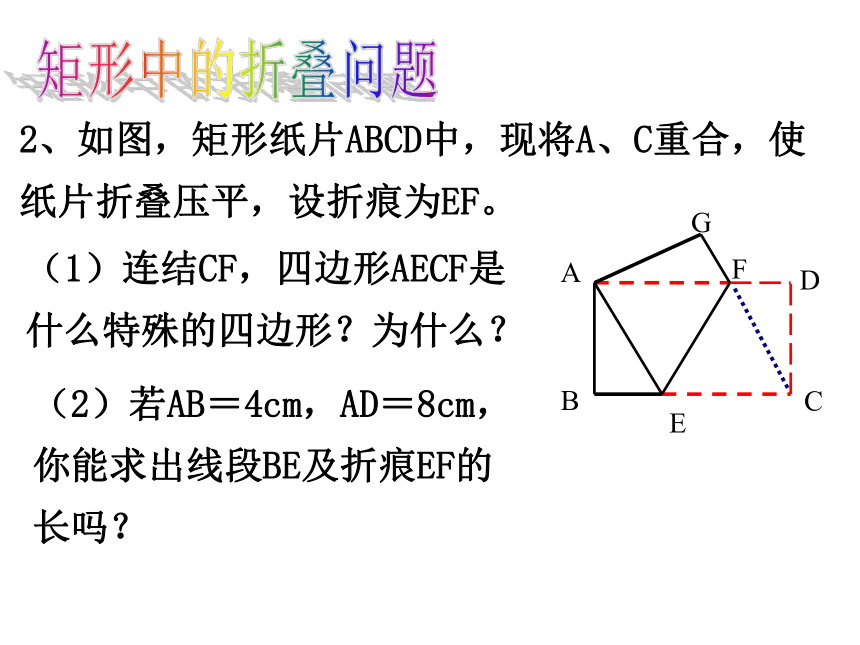
2、如图,矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF。
A
B
E
C
D
F
G
(1)连结CF,四边形AECF是什么特殊的四边形?为什么?
(2)若AB=4cm,AD=8cm,你能求出线段BE及折痕EF的长吗?
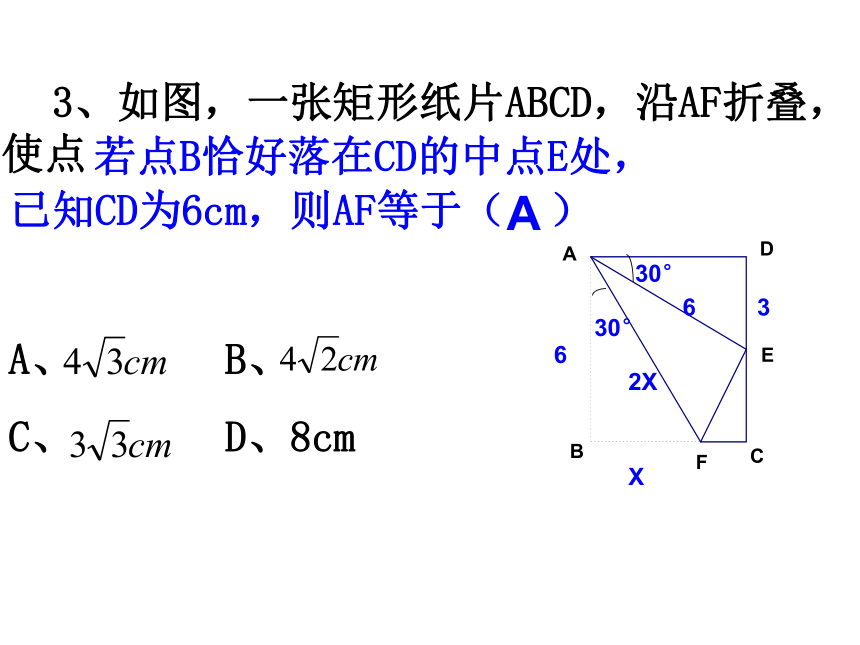
3、如图,一张矩形纸片ABCD,沿AF折叠,使点B落在CD边上。若∠AFB=55°,那么∠FEC= 。
已知CD为6cm,则AF等于( )
A、 B、
C、 D、8cm
若点B恰好落在CD的中点E处,
6
6
3
30°
30°
X
2X
A
4、 如图,矩形纸片ABCD中,AB=3厘米,BC=4厘米,现将A、C重合,使纸片折叠压平,设折痕为EF。试确定重叠部分△AEF的面积。
A
B
E
C
D
F
G
1
2
3
X
4-X
4-X
5、矩形ABCD中,AB=3,BC=4,P是边AD上的动点,PE⊥AC,PF⊥BD,
PE∥OD,PF∥OA,
A
B
C
D
P
E
F
O
O
(2)求PE+PF的值。
(1)在△ACD中,试求AC边上的高。
6、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。
(1)求对角线OB所在直线的解析式;
O
C
A
B
x
y
6、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。
(2)如图,将△OAB沿对角线OB翻折得到△OBN,ON与AB交于点M。
O
C
A
B
x
y
② 试求直线MN的解析式.
① 判断△OBM是什么三角形,并说明理由;
折叠型问题在“大小”方面的应用,通常有求线段的长,角的度数,图形的周长与面积的变化关系等问题。
一、在“大小”方面的应用
1、求线段与线段的大小关系
例1 如图,AD是 ABC的中线, ADC=45 ,把 ADC沿AD对折,点C落在点C'的位置,求BC'与BC之间的数量关系。
解 由轴对称可知 ADC ≌ ADC' , ADC'= ADC=45 , C'D=CD=BD
BC D为Rt BC’= 2 BD= BC
2
2
练习1 如图,有一块直角三角形纸片,两直角边AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ) (A)2 (B)3 (C )4 (D)5
例2 如图,折叠矩形的一边AD,点D落在BC边上点F处,已知AB=8,BC=10,则EC的长是 。
解 设EC=x,则DE=8-x,由轴对称可知:EF=DE=8-x,AF=AD=10,又因AB=8,故BF=6,故FC=BC-BF=4。在Rt FCE中,42+x2=(8-x)2,解之得x=3
B
练习2 如图,将矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线MN上,若AB= 3,则折痕AE的长为( )。 (A) 3 3/2 (B) 3 3/4 (C ) 2 (D) 2 3
E
C
2、求角的度数
例3 将长方形ABCD的纸片,沿EF折成如图所示;已知 EFG=55 ,则 FGE= 。
70
练习3如图,矩形ABCD沿BE折叠,使点C落在AD边上的F点处,如果 ABF=60 ,则 CBE等于( )。 (A)15 (B)30 (C )45 (D)60
A
练习4 如图,将矩形纸片ABCD沿一对角线BD折叠一次(折痕与折叠后得到的图形用虚线表示),将得到的所有的全等三角形(包括实线、虚线在内)用符号写出来。
练习5 如图,矩形纸片ABCD,若把 ABE沿折痕BE上翻,使A点恰好落在CD上,此时,AE:ED=5:3,BE=5 5,求矩形的长和宽。
答案:△ABD≌△CDB, △CDB≌△EDB, △EDB≌△ABD, △ABF≌△EDF.
答案:矩形的长为10,宽为8。
4、求线段与面积间的变化关系
例5 已知一三角形纸片ABC,面积为25,BC的长为10, B和 C都为锐角,M为AB上的一动点(M与A、B不重合),过点M作MN∥BC,交AC于点N,设MN=x. (1)用x表示△AMN的面积SΔAMN。 (2)ΔAMN沿MN折叠,设点A关于ΔAMN对称的点为A ,ΔA MN与四边形BCMN重叠部分的面积为y.①试求出y与x的函数关系式,并写出自变量X的取值范围;
例6 将长方形ABCD的纸片,沿EF折成如图所示,延长C`E交AD于H,连结GH。求证:EF与GH互相垂直平分。
二、在“位置”方面的应用
由于图形折叠后,点、线、面等相应的位置发生变化,带来图形间的位置关系重新组合。
1、线段与线段的位置关系
证明:由题意知FH∥GE,FG∥HE,∴ 。
又 ,
∴四边形 是 ,∴FE与GH互相垂直平分。
2、点的位置的确定
例7 已知:如图,矩形AOBC,以O为坐标原点,OB、OA分别在x轴,y轴上,点A坐标为(0,3),∠OAB=60 ,以AB为轴对折后,使C点落在D点处,求D点坐标。
→x
↑y
解由题意知,OA=3,∠OAB=60 ,∴OB=3tan60 =3√3 .
∵Rt△ACB≌Rt△ADB, ∴AD=AC=OB=3√3 .
→x
↑y
过点D作Y轴垂线,垂足为E,
在直角三角形AED中,ED= ,AE= ,故OE= 。
故点D的坐标为(3/2√3 ,- 3/2)。
练习7 如图,在直角三角形ABC中,∠C=90 ,沿着B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合。当∠A满足什么条件时,点D恰好是AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB中点。
条件:∠A=30
证明:由轴对称可得,△BCE≌△BDE,
∴ BC=BD ,
在△ABC中,∵ ∠C=90 ,∠A=30 ,
∴ BC= AB ,
∴ BD = AB ,即点D为AB的中点。
5
4
3
P
D
C
B
A
2、如图,P是矩形ABCD内一点,
PA=3,PD=4,PC=5,
则PB= 。
∟
E
F
提示:过点P作其中一边的垂线,利用勾股定理来解。
面积类应用题:
1.如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( )
A.1米 B.1.5米 C.2米 D.2.5米
A
面积类应用题:
2.如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
⑴怎样围才能使矩形场地的面积为750m2
⑵能否使所围矩形场地的面积为810m2,为什么
B
A
D
C
墙
增长率类应用题:
3.2008年爆发的世界金融危机,是自上世纪三十年代以来世界最严重的一场金融危机。受金融危机的影响,某商品原价为200元,连续两次降价a%后售价为148元,下面所列方程正确的是( )
A.200(1+a%)2=148; B.200(1-a%)2=148;
C.200(1-2a%)=148; D.200(1+a2%)=148;
B
A
B
C
P
Q
(1)用含x的代数式表
示BQ、PB的长度;
(2)当为何值时,△PBQ为等腰三角形;
(3)是否存在x的值,使得四边形APQC的面积等于20cm2?若存在,请求出此时x的值;若不存在,请说明理由。
其它类型应用题:
4.如图,Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止。连结PQ。设动点运动时间为x秒。
其它类型应用题:
5.在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,沿线段CB 以每秒1个单位长度的速度向点B运动. 点P、Q分别从点D、C同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.
问:当t为何值时,△BPQ是等腰三角形?
A
D
B
C
P
Q
分类讨论思想
或
A
B
P
D
C
已知△ABP的一边AB=
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
设DP=a,请用含a的代数式 表示AP,BP.则AP=_____,BP=_____。
当a=3,则PA+PB=____
拓展题:
①则AD=____ BC=____
1
2
②
当a=1 时,则PA+PB=____,
③
PA+PB是否存在一个最小值?
④
A
B
E
C
D
F
G
中
1、定义:
有一个角是 的 叫矩形。
2、性质和判定:
性 质 判 定
边
角
对角线
同平行四边形
平行四边形
直角
四个角都是直角
对角线相等且互相平分
3、对角线相等的平行四边形.
2、有三个角是直角的四边形.
1、有一个角是直角的平行四边形.
A
B
C
D
∟
∟
∟
∟
O
中
3、直角三角形的性质及判定方法:
角:
直角三角形两锐角互余。
线段:
边角关系:
1、勾股定理:两直角边的平方和等于斜边
的平方。
2、斜边中线的性质:直角三角形斜边中线
等于斜边的一半。
1、直角三角形中,30°角所对的直角边
等于斜边的一半。
2、直角三角形中,若直角边等于斜边的一半,
那么这条直角边所对的角等于30°。
A
B
C
D
中
1、已知矩形的一条对角线与一边的夹角
是40°,则两条对角线所成的锐角的
度数是( )
A、100° B、90° C、80° D、70°
2、矩形的一边长为6,各边中点围成的四
边形的周长是20 ,则矩形的对角线长
为 ,面积为 。
3、平行四边形四个内角的平分线,如果能围成
一个四边形,那么这个四边形一定是( )
A、矩形 B、菱形
C、正方形 D、等腰梯形
4、如图,矩形ABCD中,O是对角线的交点,
若AE⊥BD于E,且
OE∶OD=1∶2,
AE= cm,
则∠AOD = ,
DE= cm。
5、已知:如图,在 ABCD 中,E、F分别为边
AB、CD的中点,BD是对角线,AG∥DB交CB的
延长线于G.
(1)求证:DE=BF;
(2)若四边形 BEDF是
菱形,则四边形
AGBD是什么特殊
四边形?并证明
你的结论.
1、如图,将矩形ABCD沿AE折叠,使点D落
在BC边上的F点处。
(1)若∠BAF=60°,求∠EAF的度数;
(2)若AB=6cm,
AD=10cm,
求线段CE的
长及△AEF的
面积.
2、如图,矩形纸片ABCD中,现将A、C重合,使纸片折叠压平,设折痕为EF。
A
B
E
C
D
F
G
(1)连结CF,四边形AECF是什么特殊的四边形?为什么?
(2)若AB=4cm,AD=8cm,你能求出线段BE及折痕EF的长吗?
3、如图,一张矩形纸片ABCD,沿AF折叠,使点B落在CD边上。若∠AFB=55°,那么∠FEC= 。
已知CD为6cm,则AF等于( )
A、 B、
C、 D、8cm
若点B恰好落在CD的中点E处,
6
6
3
30°
30°
X
2X
A
4、 如图,矩形纸片ABCD中,AB=3厘米,BC=4厘米,现将A、C重合,使纸片折叠压平,设折痕为EF。试确定重叠部分△AEF的面积。
A
B
E
C
D
F
G
1
2
3
X
4-X
4-X
5、矩形ABCD中,AB=3,BC=4,P是边AD上的动点,PE⊥AC,PF⊥BD,
PE∥OD,PF∥OA,
A
B
C
D
P
E
F
O
O
(2)求PE+PF的值。
(1)在△ACD中,试求AC边上的高。
6、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。
(1)求对角线OB所在直线的解析式;
O
C
A
B
x
y
6、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。
(2)如图,将△OAB沿对角线OB翻折得到△OBN,ON与AB交于点M。
O
C
A
B
x
y
② 试求直线MN的解析式.
① 判断△OBM是什么三角形,并说明理由;
折叠型问题在“大小”方面的应用,通常有求线段的长,角的度数,图形的周长与面积的变化关系等问题。
一、在“大小”方面的应用
1、求线段与线段的大小关系
例1 如图,AD是 ABC的中线, ADC=45 ,把 ADC沿AD对折,点C落在点C'的位置,求BC'与BC之间的数量关系。
解 由轴对称可知 ADC ≌ ADC' , ADC'= ADC=45 , C'D=CD=BD
BC D为Rt BC’= 2 BD= BC
2
2
练习1 如图,有一块直角三角形纸片,两直角边AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ) (A)2 (B)3 (C )4 (D)5
例2 如图,折叠矩形的一边AD,点D落在BC边上点F处,已知AB=8,BC=10,则EC的长是 。
解 设EC=x,则DE=8-x,由轴对称可知:EF=DE=8-x,AF=AD=10,又因AB=8,故BF=6,故FC=BC-BF=4。在Rt FCE中,42+x2=(8-x)2,解之得x=3
B
练习2 如图,将矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线MN上,若AB= 3,则折痕AE的长为( )。 (A) 3 3/2 (B) 3 3/4 (C ) 2 (D) 2 3
E
C
2、求角的度数
例3 将长方形ABCD的纸片,沿EF折成如图所示;已知 EFG=55 ,则 FGE= 。
70
练习3如图,矩形ABCD沿BE折叠,使点C落在AD边上的F点处,如果 ABF=60 ,则 CBE等于( )。 (A)15 (B)30 (C )45 (D)60
A
练习4 如图,将矩形纸片ABCD沿一对角线BD折叠一次(折痕与折叠后得到的图形用虚线表示),将得到的所有的全等三角形(包括实线、虚线在内)用符号写出来。
练习5 如图,矩形纸片ABCD,若把 ABE沿折痕BE上翻,使A点恰好落在CD上,此时,AE:ED=5:3,BE=5 5,求矩形的长和宽。
答案:△ABD≌△CDB, △CDB≌△EDB, △EDB≌△ABD, △ABF≌△EDF.
答案:矩形的长为10,宽为8。
4、求线段与面积间的变化关系
例5 已知一三角形纸片ABC,面积为25,BC的长为10, B和 C都为锐角,M为AB上的一动点(M与A、B不重合),过点M作MN∥BC,交AC于点N,设MN=x. (1)用x表示△AMN的面积SΔAMN。 (2)ΔAMN沿MN折叠,设点A关于ΔAMN对称的点为A ,ΔA MN与四边形BCMN重叠部分的面积为y.①试求出y与x的函数关系式,并写出自变量X的取值范围;
例6 将长方形ABCD的纸片,沿EF折成如图所示,延长C`E交AD于H,连结GH。求证:EF与GH互相垂直平分。
二、在“位置”方面的应用
由于图形折叠后,点、线、面等相应的位置发生变化,带来图形间的位置关系重新组合。
1、线段与线段的位置关系
证明:由题意知FH∥GE,FG∥HE,∴ 。
又 ,
∴四边形 是 ,∴FE与GH互相垂直平分。
2、点的位置的确定
例7 已知:如图,矩形AOBC,以O为坐标原点,OB、OA分别在x轴,y轴上,点A坐标为(0,3),∠OAB=60 ,以AB为轴对折后,使C点落在D点处,求D点坐标。
→x
↑y
解由题意知,OA=3,∠OAB=60 ,∴OB=3tan60 =3√3 .
∵Rt△ACB≌Rt△ADB, ∴AD=AC=OB=3√3 .
→x
↑y
过点D作Y轴垂线,垂足为E,
在直角三角形AED中,ED= ,AE= ,故OE= 。
故点D的坐标为(3/2√3 ,- 3/2)。
练习7 如图,在直角三角形ABC中,∠C=90 ,沿着B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合。当∠A满足什么条件时,点D恰好是AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB中点。
条件:∠A=30
证明:由轴对称可得,△BCE≌△BDE,
∴ BC=BD ,
在△ABC中,∵ ∠C=90 ,∠A=30 ,
∴ BC= AB ,
∴ BD = AB ,即点D为AB的中点。
5
4
3
P
D
C
B
A
2、如图,P是矩形ABCD内一点,
PA=3,PD=4,PC=5,
则PB= 。
∟
E
F
提示:过点P作其中一边的垂线,利用勾股定理来解。
面积类应用题:
1.如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为( )
A.1米 B.1.5米 C.2米 D.2.5米
A
面积类应用题:
2.如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
⑴怎样围才能使矩形场地的面积为750m2
⑵能否使所围矩形场地的面积为810m2,为什么
B
A
D
C
墙
增长率类应用题:
3.2008年爆发的世界金融危机,是自上世纪三十年代以来世界最严重的一场金融危机。受金融危机的影响,某商品原价为200元,连续两次降价a%后售价为148元,下面所列方程正确的是( )
A.200(1+a%)2=148; B.200(1-a%)2=148;
C.200(1-2a%)=148; D.200(1+a2%)=148;
B
A
B
C
P
Q
(1)用含x的代数式表
示BQ、PB的长度;
(2)当为何值时,△PBQ为等腰三角形;
(3)是否存在x的值,使得四边形APQC的面积等于20cm2?若存在,请求出此时x的值;若不存在,请说明理由。
其它类型应用题:
4.如图,Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止。连结PQ。设动点运动时间为x秒。
其它类型应用题:
5.在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,AD=21,DC=12,动点P从点D出发,沿线段DA方向以每秒2个单位长度的速度运动,动点Q从点C出发,沿线段CB 以每秒1个单位长度的速度向点B运动. 点P、Q分别从点D、C同时出发,当点P运动到点A时,点Q随之停止运动,设运动时间为t秒.
问:当t为何值时,△BPQ是等腰三角形?
A
D
B
C
P
Q
分类讨论思想
或
A
B
P
D
C
已知△ABP的一边AB=
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
设DP=a,请用含a的代数式 表示AP,BP.则AP=_____,BP=_____。
当a=3,则PA+PB=____
拓展题:
①则AD=____ BC=____
1
2
②
当a=1 时,则PA+PB=____,
③
PA+PB是否存在一个最小值?
④
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
