浙教八年级下册数学第四章第4节《平行四边形的判定定理(1)》(共14张PPT)
文档属性
| 名称 | 浙教八年级下册数学第四章第4节《平行四边形的判定定理(1)》(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-15 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
4.4 平行四边形的判定定理(1)
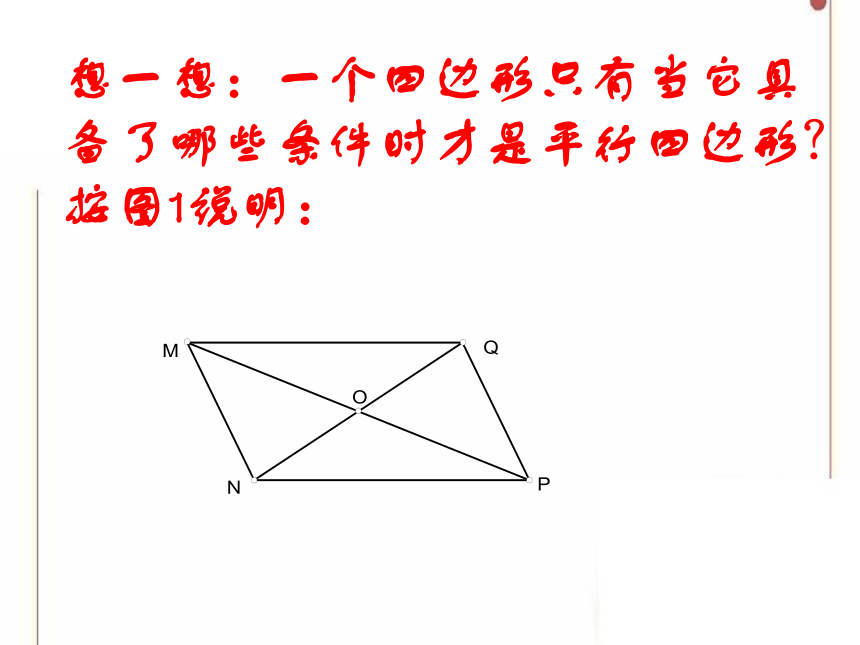
想一想:一个四边形只有当它具备了哪些条件时才是平行四边形?按图1说明:
说一说:
平行四边形有哪些性质?
性质1
平行四边形的对角相等
性质2
平行四边形的对边相等
性质3
平行四边形的对角线互相平分
找一找:
平行四边形ABCD的每一组对边有什么关系
平行四边形的对边平行且相等,这种
关系可记作AB CD
问题:请猜想“一组对边平行且相等的四边形是平行四边形”这个命题是真命题还是假命题?
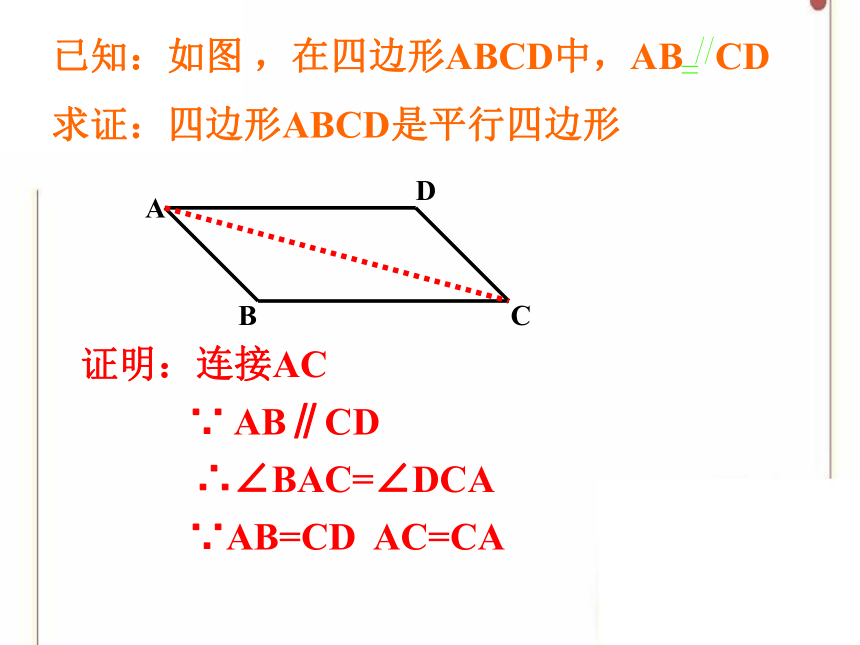
已知:如图 ,在四边形ABCD中,AB CD
求证:四边形ABCD是平行四边形
∵ AB∥CD
∴∠BAC=∠DCA
∵AB=CD AC=CA
证明:连接AC
A
B
C
D
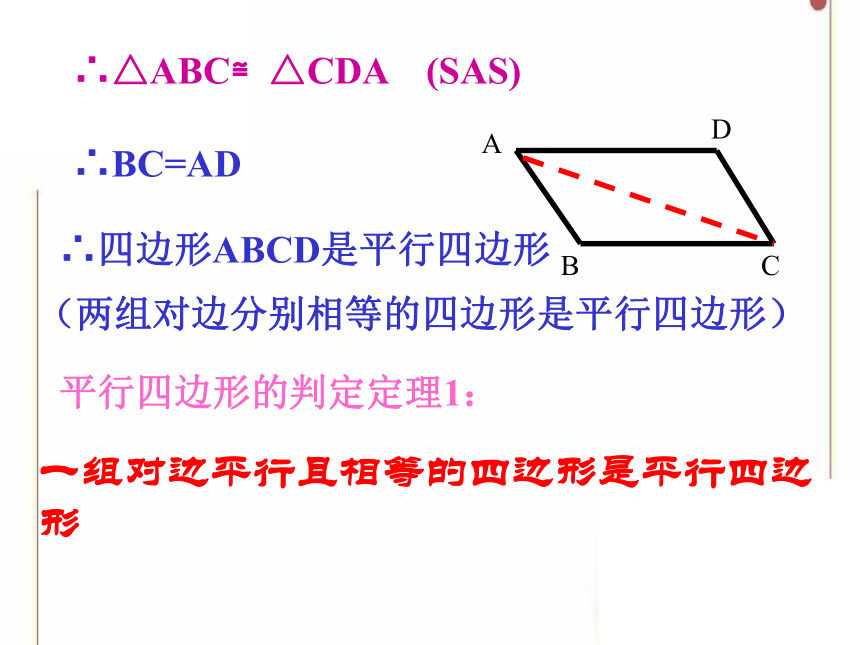
∴△ABC≌△CDA (SAS)
∴BC=AD
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形
A
B
C
D
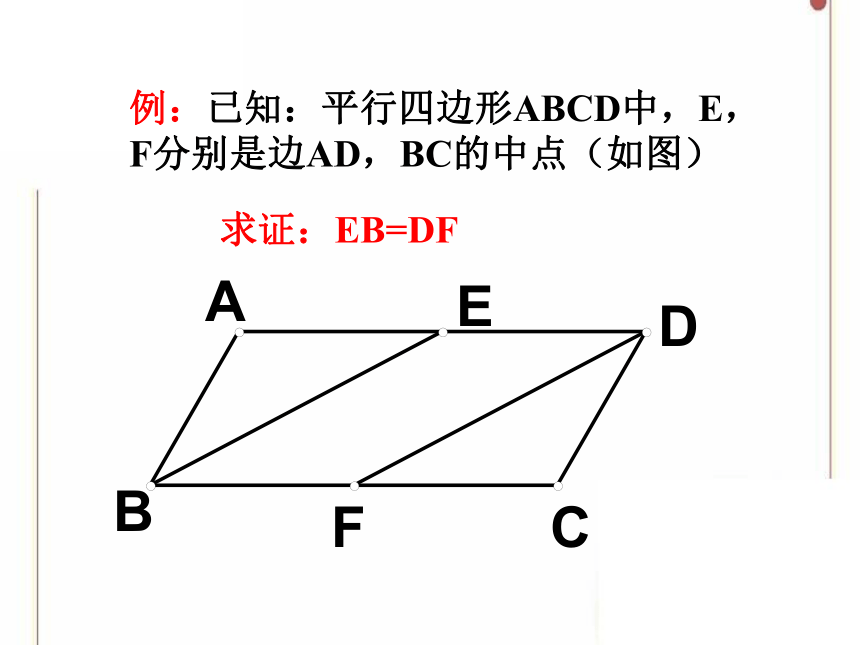
例:已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)
求证:EB=DF
例:已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)
求证:EB=DF
例:已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图)
求证:EB=DF
证明:∵四边形ABCD
是平行四边形
∴AD BC
∵ED=1/2AD BF=1/2BC
∴ED BF
∴四边形EBFD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
∴EB=DF
已知:如图,在 □ABCD 中,E,F分别是AB,CD的中点。
求证:EF∥AD
证明:∵四边形ABCD是平行四边
形,E、F分别为AB、CD的中点
∴AB DC,AE DF
∴EF AD
∴四边形AEFD是平行四边形(定理1)
练习 已知:如图,在 ABCD中,E,F分别是边 AB,CD的中点。 求证:EF//AD//BC
A
B
C
D
E
F
小结:平行四边形的三个判定方法:
从边看:
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形
作业布置:
1. P94课内练习1、2
2. 课后作业题A、B组
4.4 平行四边形的判定定理(1)
想一想:一个四边形只有当它具备了哪些条件时才是平行四边形?按图1说明:
说一说:
平行四边形有哪些性质?
性质1
平行四边形的对角相等
性质2
平行四边形的对边相等
性质3
平行四边形的对角线互相平分
找一找:
平行四边形ABCD的每一组对边有什么关系
平行四边形的对边平行且相等,这种
关系可记作AB CD
问题:请猜想“一组对边平行且相等的四边形是平行四边形”这个命题是真命题还是假命题?
已知:如图 ,在四边形ABCD中,AB CD
求证:四边形ABCD是平行四边形
∵ AB∥CD
∴∠BAC=∠DCA
∵AB=CD AC=CA
证明:连接AC
A
B
C
D
∴△ABC≌△CDA (SAS)
∴BC=AD
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形
A
B
C
D
例:已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)
求证:EB=DF
例:已知:平行四边形ABCD中,E,
F分别是边AD,BC的中点(如图)
求证:EB=DF
例:已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图)
求证:EB=DF
证明:∵四边形ABCD
是平行四边形
∴AD BC
∵ED=1/2AD BF=1/2BC
∴ED BF
∴四边形EBFD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
∴EB=DF
已知:如图,在 □ABCD 中,E,F分别是AB,CD的中点。
求证:EF∥AD
证明:∵四边形ABCD是平行四边
形,E、F分别为AB、CD的中点
∴AB DC,AE DF
∴EF AD
∴四边形AEFD是平行四边形(定理1)
练习 已知:如图,在 ABCD中,E,F分别是边 AB,CD的中点。 求证:EF//AD//BC
A
B
C
D
E
F
小结:平行四边形的三个判定方法:
从边看:
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形
作业布置:
1. P94课内练习1、2
2. 课后作业题A、B组
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
