4.1 多边形课件（2）

(共16张PPT)
四边形的内角和是多少度 怎样得到的？
四边形的外角和是多少度
四边形的内角和是360度，通过画对角线把四边形问题化归为三角形问题来解决。
四边形的外角和是360度
温故知新
我们知道 边数为3的多边形叫三角形,边数为4的多边形叫四边形.
六角螺帽
依此类推，边数为5的多边形叫五边形,……边数为n的多边形叫n边形.(n为大于或等于3的正整数)
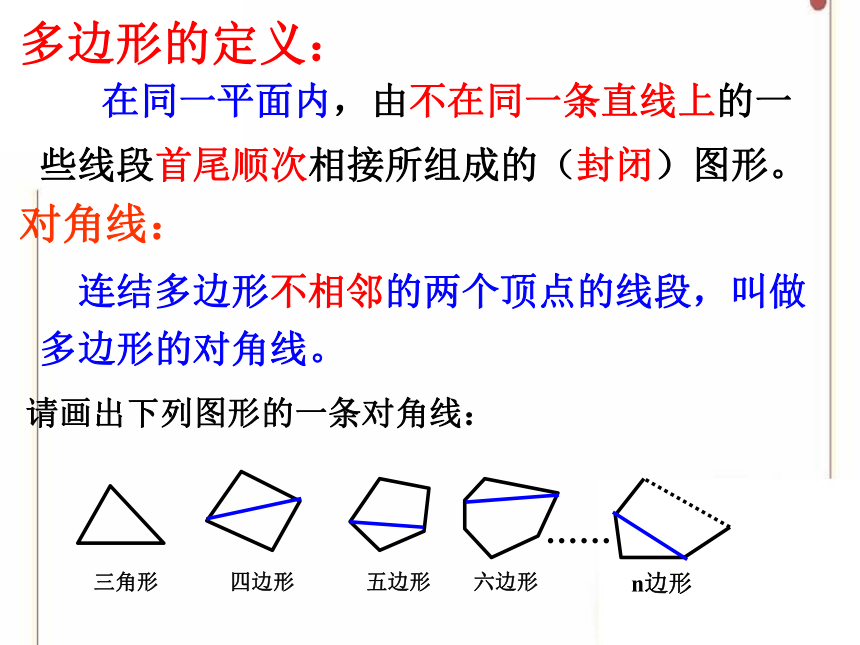
多边形的定义：
　　在同一平面内，由不在同一条直线上的一些线段首尾顺次相接所组成的（封闭）图形。
对角线：
　连结多边形不相邻的两个顶点的线段，叫做多边形的对角线。
n边形
……
三角形
四边形
五边形
六边形
请画出下列图形的一条对角线：
三角形
六边形
四边形
八边形
……..
五边形
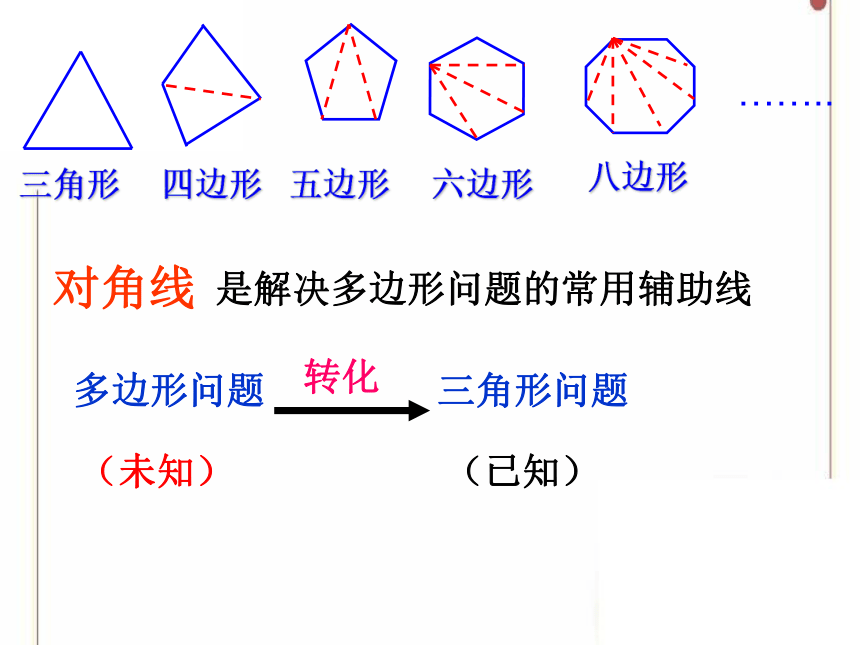
是解决多边形问题的常用辅助线
对角线
多边形问题 三角形问题
转化
（未知）
（已知）
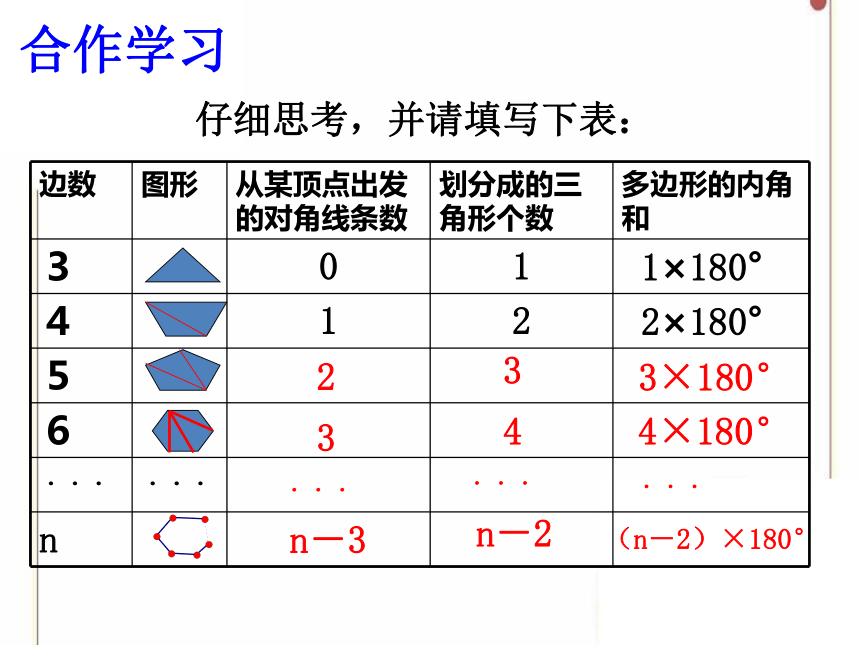
合作学习
仔细思考，并请填写下表：
边数 图形 从某顶点出发的对角线条数 划分成的三角形个数 多边形的内角和
３ 0 1 1×180°
４ 1 2 2×180°
５
６
．．． ．．．
n
2
3
3
4
3×180°
4×180°
．．．
．．．
．．．
n－3
n－2
（n－2）×180°
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-1×180o=360o
4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
n×180o-(n-2)×180o=360o
多边形的外角和
n边形的内角和为 。
n边形从一个顶点出发的对角线有 条
n边形共有对角线 条
(n－3) (n≥3)
(n≥3)
(n－2) ×180°(n≥3)
归纳小结
任何多边形的外角和等于 。
360
1、求十边形的内角和与外角和。
2、已知一个多边形的内角和为900°，这个多边形是几边形？
3、已知一个多边形的内角和为1080° ，问这个多边形是几边形？
4、已知一个多边形的每一个外角都是72°，求这个多边形的边数。
1440 °360 °
七边形
八边形
五边形
试一试
5、在五边形ABCDE中，若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80o
例2、一个六边形如图，已知AB∥DE，BC∥EF，CD∥AF，求∠A＋∠C＋∠E的度数。
A
B
C
D
E
F
1
2
3
4
解：如图所示，连结AD，
∵AB∥DE， CD∥AF（已知）
∴∠1＝∠3，∠2＝∠4
（两直线平行，内错角相等）
∴∠1+∠2＝∠3+∠4，
即∠FAB＝∠CDE，同理∠B＝∠E，∠C＝∠F
∴∠FAB＋∠C＋∠E= 1／2 ×720°=360°
∵∠FAB＋∠B＋∠C＋∠CDE＋∠E＋∠F
=（6－2）×180°= 720°
思考：有没有其它的解法？
F
E
D
C
B
A
P
R
Q
3
2
1
A
B
C
D
E
F
∵∠FAB+∠ABC+∠BCD+∠CDE＋∠DEF＋∠AFE=（6-2）×180°=720°
1
2
P
Q
R
如图所示：可向两个方向分别延长AB，CD，EF三条边，构成△PQR。
∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1＝∠2，
∴∠CDE=∠FAB
同理∠AFE＝∠BCD，∠ABC=∠DEF
∴∠FAB＋∠BCD＋∠DEF= 1／2 ×720°=360°
解法二：
1、已知六边形的各内角相等，问各内角、外角分别是多少度？
练一练
2、一个内角和为1620°的多边形有多少条对角线
3、已知六边形ABCDEF，它的各内角都相等，DE=2，EF=3，FA=1，BC=1，求六边形ABCDEF的周长、面积？
F
E
D
C
B
A
P
Q
R
练一练
练一练
4、如图，点E，F，G，H在长方形ABCD的四条边上，已知∠1=∠2=300，∠3=200。求五边形FGCHE各个内角的度数。
A
H
G
F
E
D
C
B
1
3
2
①设计一个六边形ABCDEF，使它的各内角都相等。
A
B
C
D
E
F
P
Q
R
P
E
F
Q
A
B
R
C
D
②校园里准备建造一个各边长为4米，各内角相等的六边形花坛，请画出平面图.(比例尺1：200)
（1）已知边数如何求内角和。
（2）已知内角和如何求边数。
n边形内角和等于（n -2）180°（n≥3）。
n边形的外角和等于360°。
n边形的对角线条数= （n≥3）。
说说这节课的收获和体验．