5.1 矩形课件（1）

(共12张PPT)
5.1 矩形 (1)
自主学习
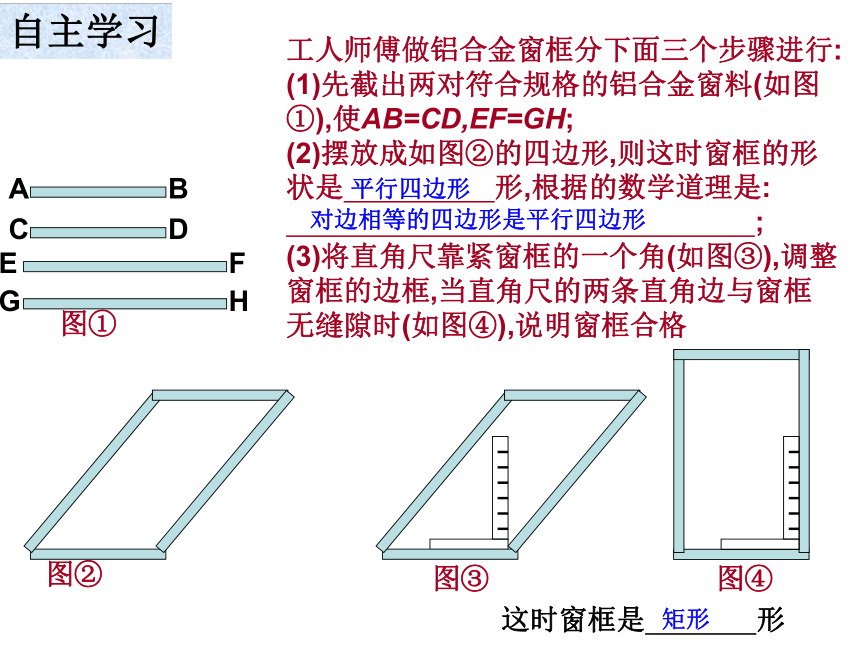
工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图
①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形
状是 形,根据的数学道理是:
;
(3)将直角尺靠紧窗框的一个角(如图③),调整
窗框的边框,当直角尺的两条直角边与窗框
无缝隙时(如图④),说明窗框合格
图①
图②
图③
图④
A
B
C
D
E
F
G
H
这时窗框是 形
平行四边形
对边相等的四边形是平行四边形
矩形
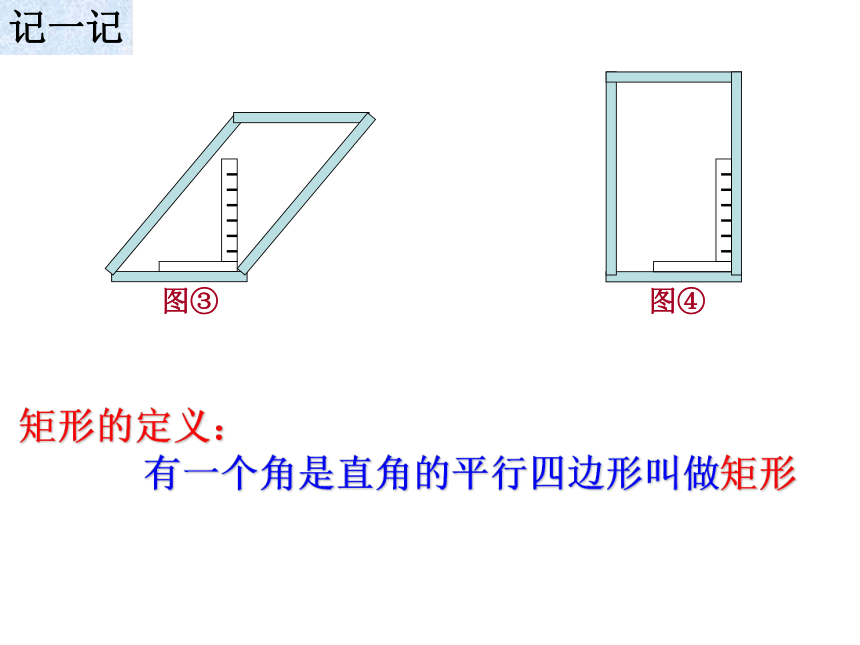
有一个角是直角的平行四边形叫做矩形
记一记
矩形的定义：
图③
图④
自主学习
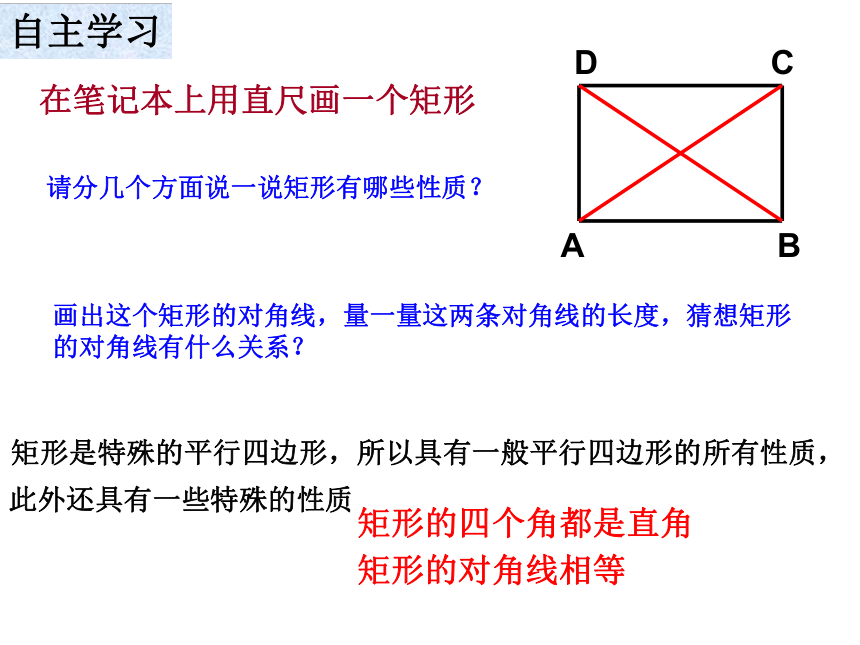
在笔记本上用直尺画一个矩形
请分几个方面说一说矩形有哪些性质？
A
B
C
D
画出这个矩形的对角线，量一量这两条对角线的长度，猜想矩形的对角线有什么关系？
矩形是特殊的平行四边形，所以具有一般平行四边形的所有性质，
此外还具有一些特殊的性质
矩形的四个角都是直角
矩形的对角线相等
探索矩形的性质
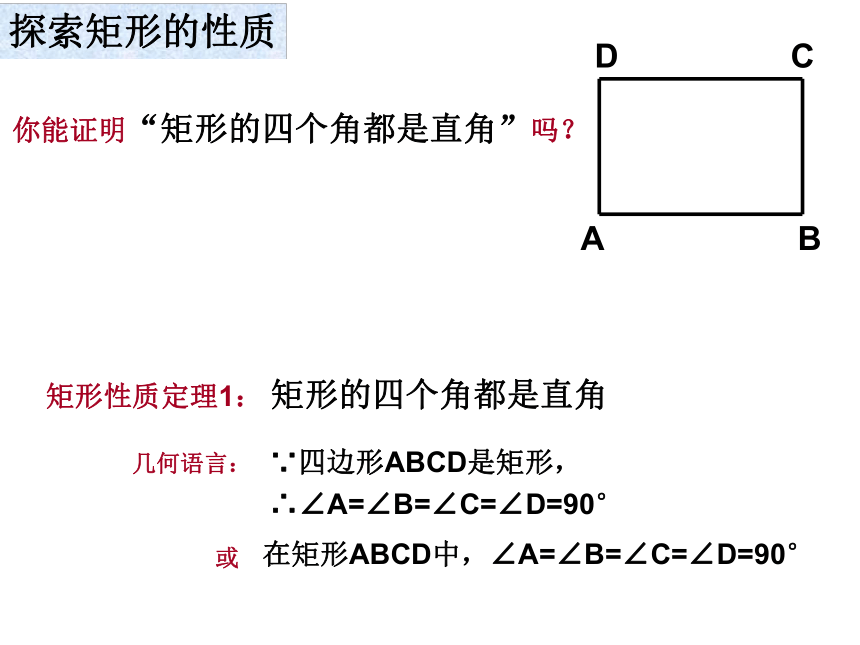
你能证明“矩形的四个角都是直角”吗？
A
B
C
D
矩形性质定理1： 矩形的四个角都是直角
几何语言：
∵四边形ABCD是矩形，
∴∠A=∠B=∠C=∠D=90°
或
在矩形ABCD中，∠A=∠B=∠C=∠D=90°
探索矩形的性质
A
B
C
D
书面证明： “矩形的对角线相等”
矩形性质定理2： 矩形的对角线相等
几何语言：
∵四边形ABCD是矩形，
∴AC=BD
或
在矩形ABCD中，AC=BD
已知：如图，AC，BD是矩形ABCD的对角线
求证：AC=BD
证明：
∴AD=BC
∠DAB=∠CBA=90°
AB=BA
∴△DAB≌△CBA
∴AC=BD
∵四边形ABCD是矩形
练习1：如图，矩形ABCD的两条对角线相交于点O
自主学习
A
B
C
D
O
（1）△AOD是什么三角形？并说明理由.图中像这样的三角形共有几个，分别是？
（2）图中有多少对全等三角形？请把它们都写出来.
例1：已知：如图，在矩形ABCD中对角线AC、BD相交于点O，∠AOD=120°，AB=4cm。
(1)判断△AOB的形状；
(2)求对角线的长；
自主学习
∴△AOB是等边三角形
（2）∵AB=4，
∴AC=BD=2AB=8
解：（1）∵四边形ABCD是矩形，
∴AC=BD
∴OA=OB
∵∠AOD=120°
∴∠AOB=60°
自主学习
练习2：如图，在矩形ABCD中，E，F分别是AB，CD的中点.
求证：四边形AEFD是矩形
A
B
C
D
E
F
定义：有一个角是直角的平行四边形是矩形
A
B
C
D
O
矩形的对称性:
矩形是中心对称图形,又是轴对称图形。
矩形的对称中心在哪？
矩形是对称轴有几条
探索矩形的其他性质
做一做：P114 课内练习3
本节课你学到什么？
作业：
课本P114-115
1.课后作业题 1、2、3、4必做，5、6选做　　　
2.预习下一节课