3.3垂径定理 浙教版初中数学九年级上册同步练习(含解析)
文档属性
| 名称 | 3.3垂径定理 浙教版初中数学九年级上册同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.3垂径定理浙教版初中数学九年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在农政全书中用图画描绘了筒车的工作原理,如图筒车盛水桶的运行轨道是以轴心为圆心的圆,如图已知圆心在水面上方,且被水面截得的弦长为米,半径长为米若点为运行轨道的最低点,则点到弦所在直线的距离是( )
A. 米 B. 米 C. 米 D. 米
2.如图,是的直径,弦于点,,,则的长为
( )
A. B. C. D.
3.如图,在圆内有折线,其中,,,则的长为( )
A.
B.
C.
D.
4.如图,是的直径,弦交于点,,,,则的长为( )
A. B. C. D.
5.高速公路的隧道和桥梁最多,如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径( )
A. 米 B. 米 C. 米 D. 米
6.如图,是的直径,弦交于点,,,,则的长为( )
A.
B.
C.
D.
7.如图,在直角坐标系中,直线交轴于点,交轴于点,以坐标原点为圆心,以为半径作交直线于点,则的值( )
A.
B.
C.
D.
8.如图,点在的直径上,作正方形和正方形,其中点,在直径所在直线上,点,,,都在上,若两个正方形的面积之和为,,则的长是( )
A.
B.
C.
D.
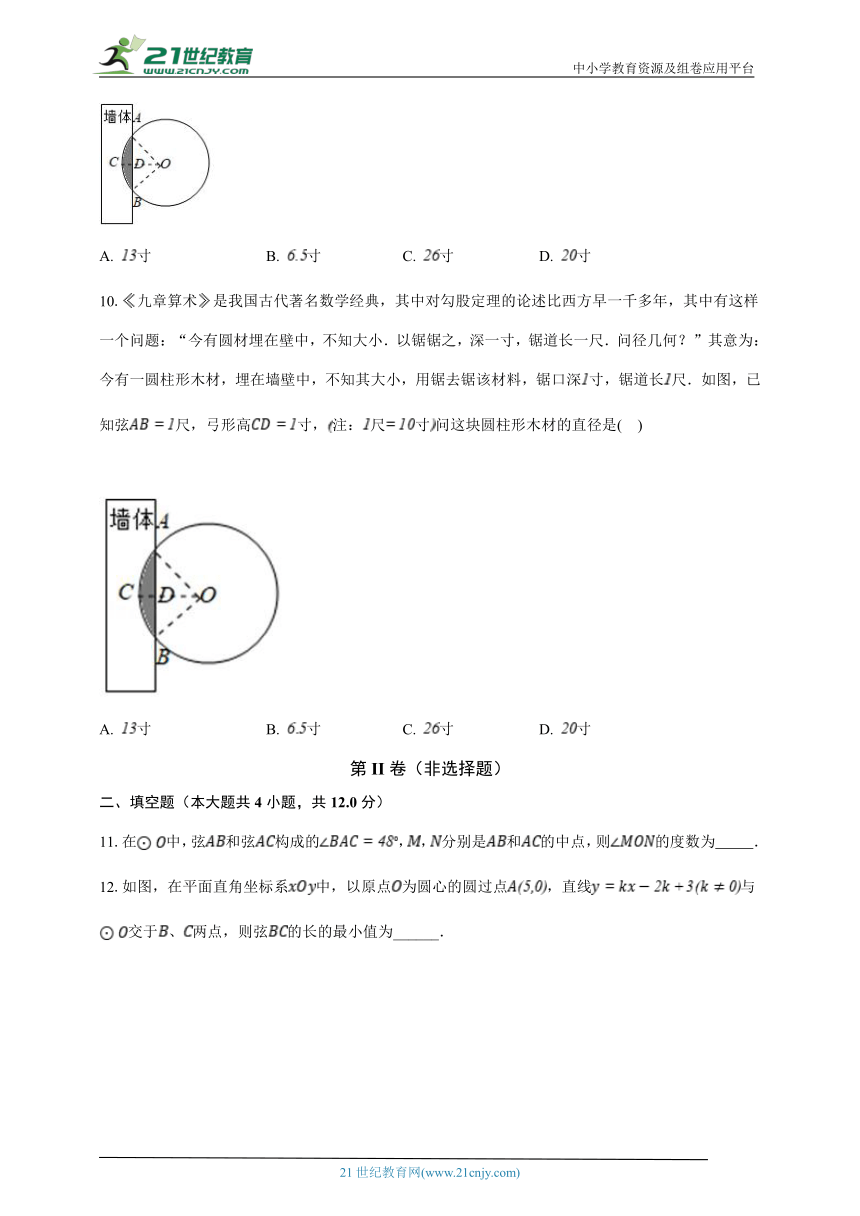
9.九章算术是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年其中有这样一个问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小用锯去锯该材料,锯口深寸,锯道长尺,如图,已知弦尺,弓形高寸注:尺寸,问这块圆柱形木材的直径是( )
A. 寸 B. 寸 C. 寸 D. 寸
10.九章算术是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深寸,锯道长尺.如图,已知弦尺,弓形高寸,注:尺寸问这块圆柱形木材的直径是( )
A. 寸 B. 寸 C. 寸 D. 寸
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.在中,弦和弦构成的,,分别是和的中点,则的度数为 .
12.如图,在平面直角坐标系中,以原点为圆心的圆过点,直线与交于、两点,则弦的长的最小值为______.
13.如图,在中,弦,点在上移动,连接,过点作交于点,则的最大值为 .
14.如图,已知半径,点为圆上的一点,点为劣弧上的一动点,,,连接,要使取得最大值,则等于_______.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
15.本小题分
如图,一座拱桥呈圆弧形,它的跨度,拱高.
求圆弧所在圆的半径的长.
当水位上涨至跨度只有时,必须采取紧急措施.若水位上涨至离拱顶,即,此时是否需采取紧急措施?
16.本小题分
如图,在中,,,,以点为圆心,为半径的圆与交于点求的长.
17.本小题分
如图,在以点为圆心的两个同心圆中,大圆的弦交小圆于点、.
求证;
若,大圆和小圆的半径分别为和,则的长度是____.
18.本小题分
如图,为一张直径为的圆形纸片,现将上任意一点与圆心重合折叠,得折痕求折痕的长.
19.本小题分
如图所示,破残的圆形轮片上,弦的垂直平分线交弧于点,交弦于点已知,.
求作此残片所在的圆不写作法,保留作图痕迹;
求中所作圆的半径.
20.本小题分
如图,是的直径,四边形内接于,交于点,.
求证:;
若,,求的长.
答案和解析
1.【答案】
【解析】【分析】
连接交于点,连接,根据垂径定理得到,根据勾股定理求出,结合图形计算,得到答案.
本题考查的是垂径定理的应用,掌握垂直于弦的直径平分这条弦是解题的关键.
【解答】
解:连接交于点,连接,
点为运行轨道的最低点,
,
米,
在中,米,
点到弦所在直线的距离米,
故选:.
2.【答案】
【解析】【分析】
此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.根据垂径定理可以得到的长,在直角中,根据勾股定理即可求得.
【解答】
解:为圆的直径,弦,垂足为点.
.
在直角中,
.
则.
故选A
3.【答案】
【解析】【分析】
此题主要考查了等边三角形的判定和性质,垂径定理的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
延长交于,根据、的度数易证得是等边三角形,由此可求出、的长;过作的垂线,设垂足为;在中,根据的长及的度数易求得的长,进而可求出的长;由垂径定理知,由此得解.
【解答】
解:延长交于,作于.
,
;
为等边三角形;
;
,
又,
;
;
;
故选:.
4.【答案】
【解析】如图,过点作于点,连结.,.
,,,,.
在中,,.
在中,,,,.
5.【答案】
【解析】【分析】
本题考查垂径定理,勾股定理,关键是应用勾股定理列出关于半径的方程,设的半径是米,由垂径定理,勾股定理,列出关于的方程,即可求解.
【解答】
解:设的半径是米,
,
米,
,
,
,
的半径是米.
故选A.
6.【答案】
【解析】【分析】
本题考查了垂径定理.也考查了勾股定理以及含度的直角三角形的性质.
作于,连结,如图,根据垂径定理由得到,再利用,可计算出半径,则,接着在中根据含度的直角三角形的性质计算出,然后在中利用勾股定理计算出,即.
【解答】
解:作于,连结,如图,
,
,
,,
,
,
,
在中,
,
,
在中,
,,
故选C.
7.【答案】
【解析】解:如图,过点作于点,则,
直线交轴于点,交轴于点,
,,
在中,,,由勾股定理得,
,
,
在中,,,由勾股定理得,
,
.
故选:.
过点作于点,则由垂径定理可得;由直线交轴于点,交轴于点,分别得出点和点的坐标,由勾股定理得出的值;再由面积法得出的长;然后由勾股定理求得的长,则的值也可得,最后用的长减去和的长即为的长.
本题考查了垂径定理、一次函数在几何问题中的应用、面积法及勾股定理等知识点,熟练掌握相关性质及定理是解题的关键.
8.【答案】
【解析】解:作于,设正方形的边长是,
四边形是正方形,
,
,
是等腰直角三角形,
,
,
,
两个正方形的面积之和为,
,
或舍,
,,
,,
.
故选:.
设正方形的边长是,由条件得到,从而求出正方形的边长,得到正方形的边长,进一步求出,的长,即可求出的长.
本题考查正方形的性质,垂径定理,关键是由条件列出关于小正方形边长的方程,求出小正方形边长.
9.【答案】
【解析】解:设的半径为.
在中,,,,
则有,
解得,
的直径为寸,
故选:.
设的半径为在中,,,,则有,解方程即可;
本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
10.【答案】
【解析】解:设的半径为.
在中,,,,
则有,
解得,
的直径为寸,
故选:.
本题考查垂径定理的应用、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.设的半径为在中,,,,则有,解方程即可.
11.【答案】或
【解析】【分析】
本题主要考查了垂径定理,分类讨论,数形结合是解答此题的关键.
连接,,利用垂径定理得,,再分类讨论,当,在圆心异侧时如图,利用四边形内角和得结果;当,在圆心同侧时如图,利用等角的余角相等得结果.
【解答】
解:连结,,
,分别是和的中点,
,.
当,在圆心异侧时,如图,在四边形中,
,
当,在圆心同侧时,如图,
,,
即.
综上,的度数为或.
12.【答案】
【解析】【分析】
本题主要考查了直线上点的坐标特征、垂径定理、勾股定理等知识,发现直线恒经过点以及运用“过圆内定点的所有弦中,与垂直的弦最短”这个经验是解决该选择题的关键.
易知直线过定点,运用勾股定理可求出,由条件可求出半径,由于过圆内定点的所有弦中,与垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题.
【解答】
解:对于直线,当时,,
故直线恒经过点,记为点.
过点作轴于点,
则有,,
.
过点,
,
.
由于过圆内定点的所有弦中,与垂直的弦最短,如图所示,
因此运用垂径定理及勾股定理可得:
的最小值为.
故答案为.
13.【答案】
【解析】【分析】
本题考查了垂线段最短,勾股定理和垂径定理等知识点,能求出点的位置是解此题的关键.
连接,如图,利用勾股定理得到,利用垂线段最短得到当时,最小,根据勾股定理求出,代入求出即可.
【解答】
解:连接,如图,
,
,
,
当的值最小时,的值最大,
而时,最小,此时,
的最大值为,
故答案为:.
14.【答案】
【解析】解:如图,延长交于,延长交于,连接.
,,
,,
,
当是直径时,的长最大,
连接,
,,,
,,
,
如图,延长交于,延长交于,连接根据垂径定理以及三角形的中位线定理,可得,当是直径时,的长最大,再证明,即可解决问题.
本题考查垂径定理,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.
15.【答案】解:连结,
由题意得:,,
在中,由勾股定理得:,
解得,,
故圆弧所在的圆的半径的长为;
连结,
,
在中,由勾股定理得:
,即:,
解得:.
.
,
不需要采取紧急措施.
【解析】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
连结,利用表示出的长,在中根据勾股定理求出的值即可;
连结,在中,由勾股定理得出的长,进而可得出的长,据此可得出结论.
16.【答案】解:过点作于点,
则,
,,,
,
,
,
,
.
【解析】此题考查了垂径定理、勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
首先过点作于点,由,,,可求得的长,又由直角三角形斜边上的高等于两直角边乘积除以斜边,即可求得的长,由勾股定理求得的长,然后由垂径定理求得的长.
17.【答案】证明:作于,如图,
,
,,
,
.
【解析】【分析】
本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧也考查了勾股定理.
作于,如图,根据垂径定理得到,,利用等量减等量差相等可得到结论
连接,如图,设,利用勾股定理得到,,则,然后解方程求出即可得到的长.
【解答】
见答案;
解:连接,如图,设,
在中,,
在中,,
,
解得,
.
故答案为.
18.【答案】略
【解析】略
19.【答案】解:作弦或的垂直平分线与弦的垂直平分线交于点,以为圆心,或、长为半径作圆,就是此残片所在的圆,如图.
如图,连接,设,则.
,
.
根据勾股定理列方程,得,
解得.
故所作圆的半径为.
【解析】本题主要考查了尺规作图,垂径定理,中垂线的性质,勾股定理,熟练掌握垂径定理是解决此题的关键.
由垂径定理知,垂直于弦的直径是弦的中垂线,故作,的中垂线交于点,则点是弧所在圆的圆心;
在中,由勾股定理可求得半径的长.
20.【答案】证明:,
,
,
,
是直径,
,
,
.
解:,
,
设,
在中,,
,
,
,
,,
.
【解析】这部分证明,可得结论.
利用勾股定理求出半径,再求出,利用三角形的中位线定理可得结论.
本题考查垂径定理,平行线的判定,三角形的中位线定理,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
3.3垂径定理浙教版初中数学九年级上册同步练习
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在农政全书中用图画描绘了筒车的工作原理,如图筒车盛水桶的运行轨道是以轴心为圆心的圆,如图已知圆心在水面上方,且被水面截得的弦长为米,半径长为米若点为运行轨道的最低点,则点到弦所在直线的距离是( )
A. 米 B. 米 C. 米 D. 米
2.如图,是的直径,弦于点,,,则的长为
( )
A. B. C. D.
3.如图,在圆内有折线,其中,,,则的长为( )
A.
B.
C.
D.
4.如图,是的直径,弦交于点,,,,则的长为( )
A. B. C. D.
5.高速公路的隧道和桥梁最多,如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径( )
A. 米 B. 米 C. 米 D. 米
6.如图,是的直径,弦交于点,,,,则的长为( )
A.
B.
C.
D.
7.如图,在直角坐标系中,直线交轴于点,交轴于点,以坐标原点为圆心,以为半径作交直线于点,则的值( )
A.
B.
C.
D.
8.如图,点在的直径上,作正方形和正方形,其中点,在直径所在直线上,点,,,都在上,若两个正方形的面积之和为,,则的长是( )
A.
B.
C.
D.
9.九章算术是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年其中有这样一个问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小用锯去锯该材料,锯口深寸,锯道长尺,如图,已知弦尺,弓形高寸注:尺寸,问这块圆柱形木材的直径是( )
A. 寸 B. 寸 C. 寸 D. 寸
10.九章算术是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深寸,锯道长尺.如图,已知弦尺,弓形高寸,注:尺寸问这块圆柱形木材的直径是( )
A. 寸 B. 寸 C. 寸 D. 寸
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
11.在中,弦和弦构成的,,分别是和的中点,则的度数为 .
12.如图,在平面直角坐标系中,以原点为圆心的圆过点,直线与交于、两点,则弦的长的最小值为______.
13.如图,在中,弦,点在上移动,连接,过点作交于点,则的最大值为 .
14.如图,已知半径,点为圆上的一点,点为劣弧上的一动点,,,连接,要使取得最大值,则等于_______.
三、解答题(本大题共6小题,共48.0分。解答应写出文字说明,证明过程或演算步骤)
15.本小题分
如图,一座拱桥呈圆弧形,它的跨度,拱高.
求圆弧所在圆的半径的长.
当水位上涨至跨度只有时,必须采取紧急措施.若水位上涨至离拱顶,即,此时是否需采取紧急措施?
16.本小题分
如图,在中,,,,以点为圆心,为半径的圆与交于点求的长.
17.本小题分
如图,在以点为圆心的两个同心圆中,大圆的弦交小圆于点、.
求证;
若,大圆和小圆的半径分别为和,则的长度是____.
18.本小题分
如图,为一张直径为的圆形纸片,现将上任意一点与圆心重合折叠,得折痕求折痕的长.
19.本小题分
如图所示,破残的圆形轮片上,弦的垂直平分线交弧于点,交弦于点已知,.
求作此残片所在的圆不写作法,保留作图痕迹;
求中所作圆的半径.
20.本小题分
如图,是的直径,四边形内接于,交于点,.
求证:;
若,,求的长.
答案和解析
1.【答案】
【解析】【分析】
连接交于点,连接,根据垂径定理得到,根据勾股定理求出,结合图形计算,得到答案.
本题考查的是垂径定理的应用,掌握垂直于弦的直径平分这条弦是解题的关键.
【解答】
解:连接交于点,连接,
点为运行轨道的最低点,
,
米,
在中,米,
点到弦所在直线的距离米,
故选:.
2.【答案】
【解析】【分析】
此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解,常见辅助线是过圆心作弦的垂线.根据垂径定理可以得到的长,在直角中,根据勾股定理即可求得.
【解答】
解:为圆的直径,弦,垂足为点.
.
在直角中,
.
则.
故选A
3.【答案】
【解析】【分析】
此题主要考查了等边三角形的判定和性质,垂径定理的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
延长交于,根据、的度数易证得是等边三角形,由此可求出、的长;过作的垂线,设垂足为;在中,根据的长及的度数易求得的长,进而可求出的长;由垂径定理知,由此得解.
【解答】
解:延长交于,作于.
,
;
为等边三角形;
;
,
又,
;
;
;
故选:.
4.【答案】
【解析】如图,过点作于点,连结.,.
,,,,.
在中,,.
在中,,,,.
5.【答案】
【解析】【分析】
本题考查垂径定理,勾股定理,关键是应用勾股定理列出关于半径的方程,设的半径是米,由垂径定理,勾股定理,列出关于的方程,即可求解.
【解答】
解:设的半径是米,
,
米,
,
,
,
的半径是米.
故选A.
6.【答案】
【解析】【分析】
本题考查了垂径定理.也考查了勾股定理以及含度的直角三角形的性质.
作于,连结,如图,根据垂径定理由得到,再利用,可计算出半径,则,接着在中根据含度的直角三角形的性质计算出,然后在中利用勾股定理计算出,即.
【解答】
解:作于,连结,如图,
,
,
,,
,
,
,
在中,
,
,
在中,
,,
故选C.
7.【答案】
【解析】解:如图,过点作于点,则,
直线交轴于点,交轴于点,
,,
在中,,,由勾股定理得,
,
,
在中,,,由勾股定理得,
,
.
故选:.
过点作于点,则由垂径定理可得;由直线交轴于点,交轴于点,分别得出点和点的坐标,由勾股定理得出的值;再由面积法得出的长;然后由勾股定理求得的长,则的值也可得,最后用的长减去和的长即为的长.
本题考查了垂径定理、一次函数在几何问题中的应用、面积法及勾股定理等知识点,熟练掌握相关性质及定理是解题的关键.
8.【答案】
【解析】解:作于,设正方形的边长是,
四边形是正方形,
,
,
是等腰直角三角形,
,
,
,
两个正方形的面积之和为,
,
或舍,
,,
,,
.
故选:.
设正方形的边长是,由条件得到,从而求出正方形的边长,得到正方形的边长,进一步求出,的长,即可求出的长.
本题考查正方形的性质,垂径定理,关键是由条件列出关于小正方形边长的方程,求出小正方形边长.
9.【答案】
【解析】解:设的半径为.
在中,,,,
则有,
解得,
的直径为寸,
故选:.
设的半径为在中,,,,则有,解方程即可;
本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
10.【答案】
【解析】解:设的半径为.
在中,,,,
则有,
解得,
的直径为寸,
故选:.
本题考查垂径定理的应用、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.设的半径为在中,,,,则有,解方程即可.
11.【答案】或
【解析】【分析】
本题主要考查了垂径定理,分类讨论,数形结合是解答此题的关键.
连接,,利用垂径定理得,,再分类讨论,当,在圆心异侧时如图,利用四边形内角和得结果;当,在圆心同侧时如图,利用等角的余角相等得结果.
【解答】
解:连结,,
,分别是和的中点,
,.
当,在圆心异侧时,如图,在四边形中,
,
当,在圆心同侧时,如图,
,,
即.
综上,的度数为或.
12.【答案】
【解析】【分析】
本题主要考查了直线上点的坐标特征、垂径定理、勾股定理等知识,发现直线恒经过点以及运用“过圆内定点的所有弦中,与垂直的弦最短”这个经验是解决该选择题的关键.
易知直线过定点,运用勾股定理可求出,由条件可求出半径,由于过圆内定点的所有弦中,与垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题.
【解答】
解:对于直线,当时,,
故直线恒经过点,记为点.
过点作轴于点,
则有,,
.
过点,
,
.
由于过圆内定点的所有弦中,与垂直的弦最短,如图所示,
因此运用垂径定理及勾股定理可得:
的最小值为.
故答案为.
13.【答案】
【解析】【分析】
本题考查了垂线段最短,勾股定理和垂径定理等知识点,能求出点的位置是解此题的关键.
连接,如图,利用勾股定理得到,利用垂线段最短得到当时,最小,根据勾股定理求出,代入求出即可.
【解答】
解:连接,如图,
,
,
,
当的值最小时,的值最大,
而时,最小,此时,
的最大值为,
故答案为:.
14.【答案】
【解析】解:如图,延长交于,延长交于,连接.
,,
,,
,
当是直径时,的长最大,
连接,
,,,
,,
,
如图,延长交于,延长交于,连接根据垂径定理以及三角形的中位线定理,可得,当是直径时,的长最大,再证明,即可解决问题.
本题考查垂径定理,三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题.
15.【答案】解:连结,
由题意得:,,
在中,由勾股定理得:,
解得,,
故圆弧所在的圆的半径的长为;
连结,
,
在中,由勾股定理得:
,即:,
解得:.
.
,
不需要采取紧急措施.
【解析】本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
连结,利用表示出的长,在中根据勾股定理求出的值即可;
连结,在中,由勾股定理得出的长,进而可得出的长,据此可得出结论.
16.【答案】解:过点作于点,
则,
,,,
,
,
,
,
.
【解析】此题考查了垂径定理、勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
首先过点作于点,由,,,可求得的长,又由直角三角形斜边上的高等于两直角边乘积除以斜边,即可求得的长,由勾股定理求得的长,然后由垂径定理求得的长.
17.【答案】证明:作于,如图,
,
,,
,
.
【解析】【分析】
本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧也考查了勾股定理.
作于,如图,根据垂径定理得到,,利用等量减等量差相等可得到结论
连接,如图,设,利用勾股定理得到,,则,然后解方程求出即可得到的长.
【解答】
见答案;
解:连接,如图,设,
在中,,
在中,,
,
解得,
.
故答案为.
18.【答案】略
【解析】略
19.【答案】解:作弦或的垂直平分线与弦的垂直平分线交于点,以为圆心,或、长为半径作圆,就是此残片所在的圆,如图.
如图,连接,设,则.
,
.
根据勾股定理列方程,得,
解得.
故所作圆的半径为.
【解析】本题主要考查了尺规作图,垂径定理,中垂线的性质,勾股定理,熟练掌握垂径定理是解决此题的关键.
由垂径定理知,垂直于弦的直径是弦的中垂线,故作,的中垂线交于点,则点是弧所在圆的圆心;
在中,由勾股定理可求得半径的长.
20.【答案】证明:,
,
,
,
是直径,
,
,
.
解:,
,
设,
在中,,
,
,
,
,,
.
【解析】这部分证明,可得结论.
利用勾股定理求出半径,再求出,利用三角形的中位线定理可得结论.
本题考查垂径定理,平行线的判定,三角形的中位线定理,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
