3.2实数(第2课时)课件(共19张PPT) 2023-2024学年七年级数学上册(浙教版)
文档属性
| 名称 | 3.2实数(第2课时)课件(共19张PPT) 2023-2024学年七年级数学上册(浙教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 20:54:02 | ||
图片预览





文档简介
(共19张PPT)
3.2 实数
第2课时 实数的大小比较
数学(浙教版)
七年级 上册
第3章 实数
学习目标
1.掌握实数与数轴上点的一一对应关系,运用数形结合的数学思想进行深入理解;
2.学会比较实数的大小;
温故知新
判断下列说法是否正确:
(1)无限小数都是无理数;
(2)无理数都是无限小数;
(3)带根号的数都是无理数。
×
√
×
按定义分类
讲授新课
知识点一 实数与数轴上点的一一对应关系
思考:每个有理数都可以用数轴上的点表示,那么有理数能不能将数轴排满?
无理数是否也可以用数轴上的点来表示呢?
试
一
试
你能在数轴上找到表示 的点吗?
讲授新课
如图所示,将两个边长为1的正方形分别沿对角线剪开,得到四个等腰直角三角形,即可拼成一个大正方形.容易知道,这个大正方形的面积是2,所以大正方形的边长为 .
讲授新课
这就是说,边长为1的正方形的对角线长是 .利用这个事实,我们容易在数轴上画出表示 的点,如图所示.
发现:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
概括
实数与数轴上的点是一一对应的.
讲授新课
典例精析
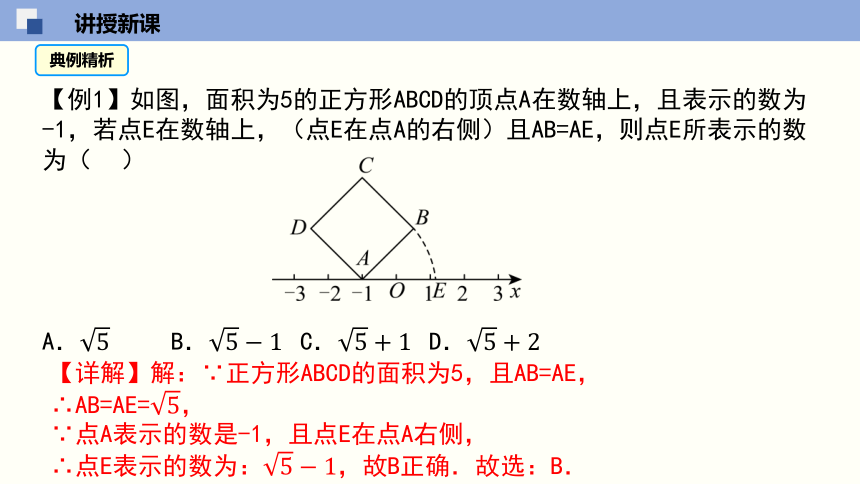
【例1】如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为-1,若点E在数轴上,(点E在点A的右侧)且AB=AE,则点E所表示的数为( )
A. B. C. D.
【详解】解:∵正方形ABCD的面积为5,且AB=AE,
∴AB=AE=,
∵点A表示的数是-1,且点E在点A右侧,
∴点E表示的数为:,故B正确.故选:B.
讲授新课
练一练
1.如图,数轴上表示实数的点可能是( )
A.点P B.点Q C.点R D.点S
【详解】解:∵4<7<9,
∴,即2<,
∴数轴上表示实数的点可能是Q,
故选:B.
讲授新课
2、如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
解析:∵ ≈1.414,∴ 和5.1之间的整数有2,3,4,5, ∴A,B两点之间表示整数的点共有4个.
C
【点睛】数轴上的点与实数一一对应,结合数轴分析,可轻松得出结论.
讲授新课
知识点二 实数的大小比较
思考:实数怎么比较大小呢?
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
讲授新课
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
总结归纳
讲授新课
,2可以看作分别是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
不用计算器, 与2比较哪个大?与3比较呢?
议一议
讲授新课
典例精析
例2: 在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
例3: 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
【点睛】熟记一些常见数的算术平方根;或用计算器估计.
讲授新课
练一练
1.比较 与 的大小.
解:因为
故
当堂检测
1.比较下列各数的大小:
(1) 与 ;(2) 与 .
解:(1)因为 所以
(2)因为4>3,所以 所以
当堂检测
2.比较下列各组数大小:
① ____6; ② ___ ;
③ ____0.5; ④ ____1.
<
<
>
<
当堂检测
3.如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
C
4.如图所示,数轴上的A,B,C ,D四点中,与数 表示的点最接近的是( )
A.点A B.点B C.点C D.点D
B
当堂检测
解:∵25< 31< 36, ∴5< < 6
∴ 的整数部分是5,
的小数部分是 -5。
归纳:小数部分=原数-整数部分
5.求 的整数部分和小数部分.
课堂小结
2、实数和数轴上的点是一一对应的.
3、与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
1、有理数和无理数都可以用数轴上的点表示.
实数的大小比较
3.2 实数
第2课时 实数的大小比较
数学(浙教版)
七年级 上册
第3章 实数
学习目标
1.掌握实数与数轴上点的一一对应关系,运用数形结合的数学思想进行深入理解;
2.学会比较实数的大小;
温故知新
判断下列说法是否正确:
(1)无限小数都是无理数;
(2)无理数都是无限小数;
(3)带根号的数都是无理数。
×
√
×
按定义分类
讲授新课
知识点一 实数与数轴上点的一一对应关系
思考:每个有理数都可以用数轴上的点表示,那么有理数能不能将数轴排满?
无理数是否也可以用数轴上的点来表示呢?
试
一
试
你能在数轴上找到表示 的点吗?
讲授新课
如图所示,将两个边长为1的正方形分别沿对角线剪开,得到四个等腰直角三角形,即可拼成一个大正方形.容易知道,这个大正方形的面积是2,所以大正方形的边长为 .
讲授新课
这就是说,边长为1的正方形的对角线长是 .利用这个事实,我们容易在数轴上画出表示 的点,如图所示.
发现:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
概括
实数与数轴上的点是一一对应的.
讲授新课
典例精析
【例1】如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为-1,若点E在数轴上,(点E在点A的右侧)且AB=AE,则点E所表示的数为( )
A. B. C. D.
【详解】解:∵正方形ABCD的面积为5,且AB=AE,
∴AB=AE=,
∵点A表示的数是-1,且点E在点A右侧,
∴点E表示的数为:,故B正确.故选:B.
讲授新课
练一练
1.如图,数轴上表示实数的点可能是( )
A.点P B.点Q C.点R D.点S
【详解】解:∵4<7<9,
∴,即2<,
∴数轴上表示实数的点可能是Q,
故选:B.
讲授新课
2、如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
解析:∵ ≈1.414,∴ 和5.1之间的整数有2,3,4,5, ∴A,B两点之间表示整数的点共有4个.
C
【点睛】数轴上的点与实数一一对应,结合数轴分析,可轻松得出结论.
讲授新课
知识点二 实数的大小比较
思考:实数怎么比较大小呢?
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
讲授新课
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
总结归纳
讲授新课
,2可以看作分别是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
不用计算器, 与2比较哪个大?与3比较呢?
议一议
讲授新课
典例精析
例2: 在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
例3: 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
【点睛】熟记一些常见数的算术平方根;或用计算器估计.
讲授新课
练一练
1.比较 与 的大小.
解:因为
故
当堂检测
1.比较下列各数的大小:
(1) 与 ;(2) 与 .
解:(1)因为 所以
(2)因为4>3,所以 所以
当堂检测
2.比较下列各组数大小:
① ____6; ② ___ ;
③ ____0.5; ④ ____1.
<
<
>
<
当堂检测
3.如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
C
4.如图所示,数轴上的A,B,C ,D四点中,与数 表示的点最接近的是( )
A.点A B.点B C.点C D.点D
B
当堂检测
解:∵25< 31< 36, ∴5< < 6
∴ 的整数部分是5,
的小数部分是 -5。
归纳:小数部分=原数-整数部分
5.求 的整数部分和小数部分.
课堂小结
2、实数和数轴上的点是一一对应的.
3、与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
1、有理数和无理数都可以用数轴上的点表示.
实数的大小比较
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
