2.2 简单事件的概率(2)课件(共16张PPT)
文档属性
| 名称 | 2.2 简单事件的概率(2)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-26 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
浙教版九年级上册
第二章 简单事件的概率
2.2 简单事件的概率(2)
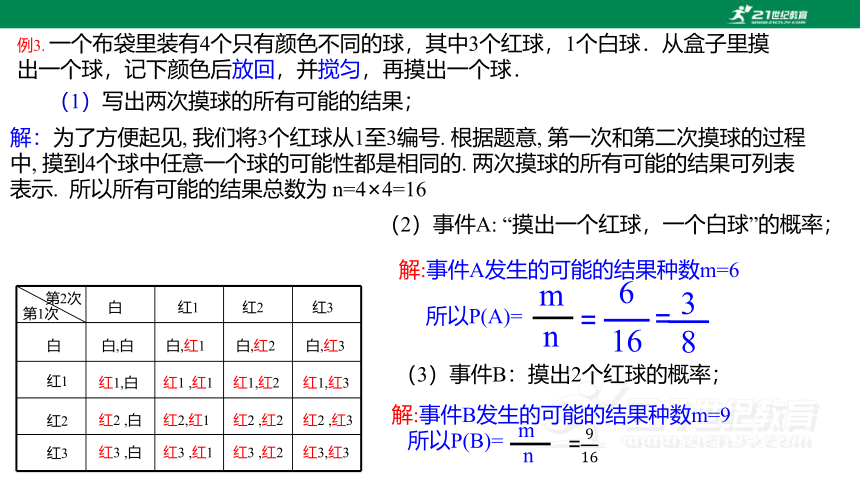
例3. 一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球.
(1)写出两次摸球的所有可能的结果;
解:为了方便起见, 我们将3个红球从1至3编号. 根据题意, 第一次和第二次摸球的过程中, 摸到4个球中任意一个球的可能性都是相同的. 两次摸球的所有可能的结果可列表表示. 所以所有可能的结果总数为 n=4×4=16
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
(2)事件A: “摸出一个红球,一个白球”的概率;
解:事件A发生的可能的结果种数m=6
所以P(A)=
n
m
=
6
16
38
=
(3)事件B:摸出2个红球的概率;
解:事件B发生的可能的结果种数m=9
所以P(B)=
n
m
=
.
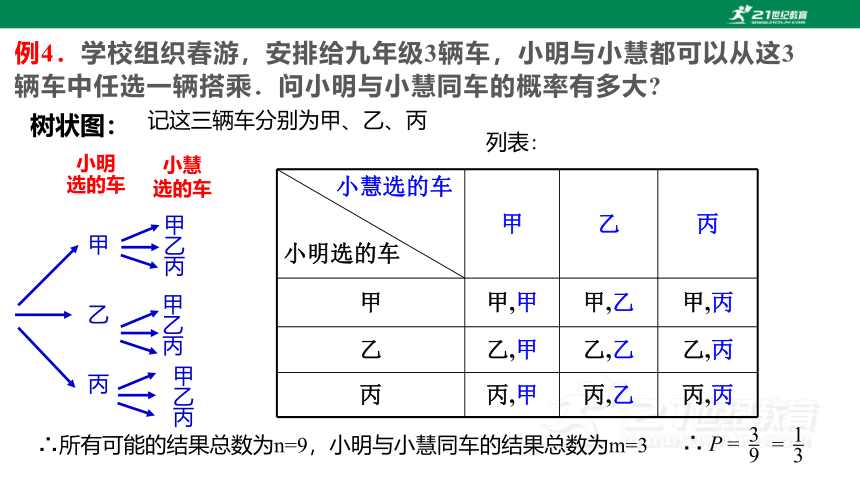
例4.学校组织春游,安排给九年级3辆车,小明与小慧都可以从这3辆车中任选一辆搭乘.问小明与小慧同车的概率有多大
树状图:
小明
选的车
小慧
选的车
甲
乙
丙
甲
乙
丙
甲
乙
丙
甲
乙
丙
记这三辆车分别为甲、乙、丙
∴所有可能的结果总数为n=9,小明与小慧同车的结果总数为m=3
∴ P =
3
9
1
3
=
小慧选的车 小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
列表:
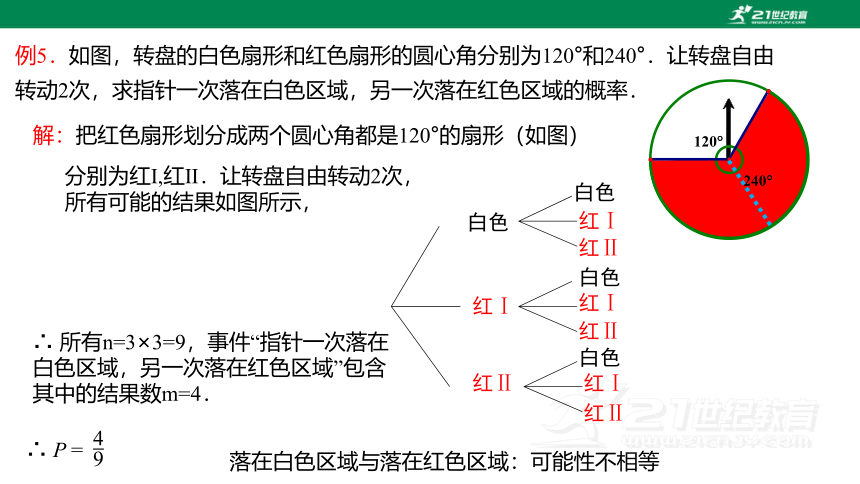
例5.如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
解:把红色扇形划分成两个圆心角都是120°的扇形(如图)
分别为红Ⅰ,红Ⅱ.让转盘自由转动2次,
所有可能的结果如图所示,
∴ 所有n=3×3=9,事件“指针一次落在白色区域,另一次落在红色区域”包含其中的结果数m=4.
∴ P =
4
9
白色
红Ⅰ
红Ⅱ
白色
红Ⅰ
红Ⅱ
白色
白色
红Ⅰ
红Ⅰ
红Ⅱ
红Ⅱ
落在白色区域与落在红色区域:可能性不相等
1.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.
1
3
黄2
开始
红
黄1
黄2
(红,黄2)
黄2
红
黄1
红
(黄1,黄2)
(黄1,红)
(黄2,黄1)
(黄2,红)
黄1
(红,黄1)
第一次
第二次
所有可能结果
夯实基础,稳扎稳打
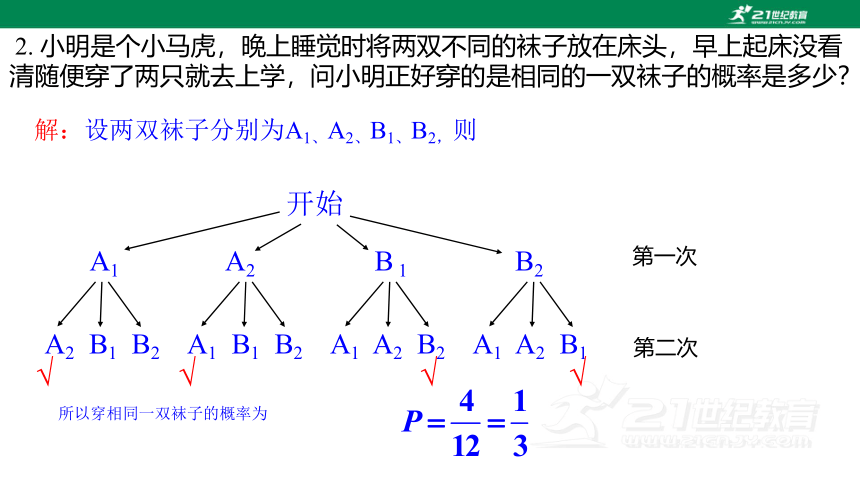
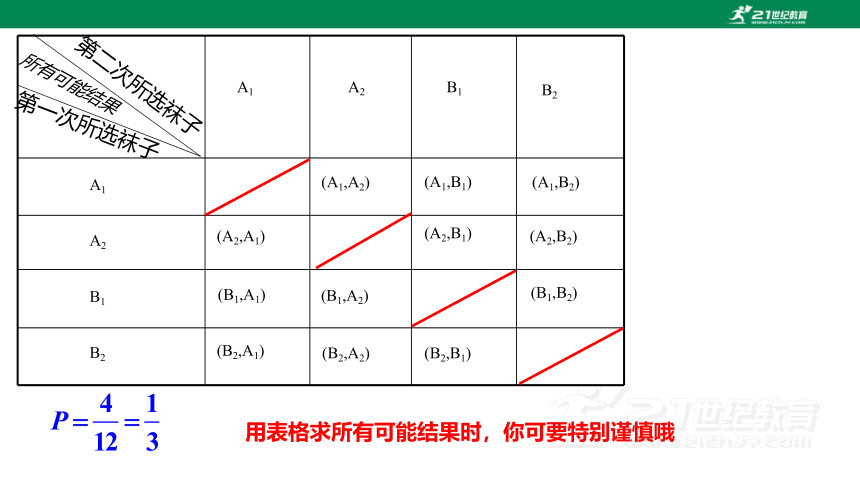
2. 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?
解:设两双袜子分别为A1、A2、B1、B2,则
开始
A1 A2 B 1 B2
A2 B1 B2 A1 B1 B2 A1 A2 B2 A1 A2 B1
√
√
√
√
所以穿相同一双袜子的概率为
第一次
第二次
第一次所选袜子
第二次所选袜子
所有可能结果
A1
A2
B1
B2
A1
A2
B1
B2
(A1,A2)
(A1,B1)
(A1,B2)
(A2,A1)
(A2,B1)
(A2,B2)
(B1,A1)
(B1,A2)
(B1,B2)
(B2,A1)
(B2,A2)
(B2,B1)
用表格求所有可能结果时,你可要特别谨慎哦
4. 小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?
解:(1)画树状图得:
∵总共有9种情况,每一种出现的机会均等,每人获胜的情形都是3种,
∴两人获胜的概率都是
小明
小刚
5.有一个转盘如图,绿色扇形的圆心角为90°,黄色扇形的圆心角为270°,让转盘自由转动2次,2次指针都落在绿色区域的概率是多少?
90°
黄1
黄2
黄3
第二次
绿
黄1
黄2
黄3
第一次
绿 黄1 黄2 黄3
绿 黄1 黄2 黄3
绿 黄1 黄2 黄3
绿 黄1 黄2 黄3
P(指针两次都落在绿色区域)=
.
6.一书架有上下两层,其中上层有2本语文书1本数学书,下层有2本语文书
2本数学书,现从上下层随机各取1本,求抽到的2本都是数学书的概率。
7. 已知一个口袋中装有7个除颜色外其他无差别的球,其中3个白球,4个黑球.从中随机取出一个球.若往口袋中再放入x个白球和y个黑球,使得取出白球的概率是 ,求y与x之间的函数关系式.
连续递推,豁然开朗
8.校园足球燃激情,绿茵场上展风采.甲、乙、丙三人在练习互相传球,规则是:第一次传球由甲将球随机地传给乙、丙中的某一人,以后的每一次传球都是由持球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在乙手中的概率;
解:画树状图如图:
两次传球后的所有结果有4种,每种结果发生的可能性相等,球恰好在乙手中
(记为事件A)的结果有1种,
(2)求三次传球后,球恰在甲手中的概率.
三次传球后的所有结果有8种,每种结果发生的可能性相等,其中球恰在甲手中
(记为事件B)的结果有2种,
树状图:
第一次传球由甲将球随机地传给乙、丙中的某一人,以后的每一次传球都是由持球者随机地传给其他两人中的某一人.
9.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
第二章 简单事件的概率
2.2 简单事件的概率(2)
例3. 一个布袋里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球.
(1)写出两次摸球的所有可能的结果;
解:为了方便起见, 我们将3个红球从1至3编号. 根据题意, 第一次和第二次摸球的过程中, 摸到4个球中任意一个球的可能性都是相同的. 两次摸球的所有可能的结果可列表表示. 所以所有可能的结果总数为 n=4×4=16
第1次
第2次
白
红1
红2
红3
白
红1
红2
红3
白,白
白,红1
白,红2
白,红3
红1,白
红1 ,红1
红1,红2
红1,红3
红2 ,白
红2,红1
红2 ,红2
红2 ,红3
红3 ,白
红3 ,红1
红3 ,红2
红3,红3
(2)事件A: “摸出一个红球,一个白球”的概率;
解:事件A发生的可能的结果种数m=6
所以P(A)=
n
m
=
6
16
38
=
(3)事件B:摸出2个红球的概率;
解:事件B发生的可能的结果种数m=9
所以P(B)=
n
m
=
.
例4.学校组织春游,安排给九年级3辆车,小明与小慧都可以从这3辆车中任选一辆搭乘.问小明与小慧同车的概率有多大
树状图:
小明
选的车
小慧
选的车
甲
乙
丙
甲
乙
丙
甲
乙
丙
甲
乙
丙
记这三辆车分别为甲、乙、丙
∴所有可能的结果总数为n=9,小明与小慧同车的结果总数为m=3
∴ P =
3
9
1
3
=
小慧选的车 小明选的车 甲 乙 丙
甲 甲,甲 甲,乙 甲,丙
乙 乙,甲 乙,乙 乙,丙
丙 丙,甲 丙,乙 丙,丙
列表:
例5.如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率.
解:把红色扇形划分成两个圆心角都是120°的扇形(如图)
分别为红Ⅰ,红Ⅱ.让转盘自由转动2次,
所有可能的结果如图所示,
∴ 所有n=3×3=9,事件“指针一次落在白色区域,另一次落在红色区域”包含其中的结果数m=4.
∴ P =
4
9
白色
红Ⅰ
红Ⅱ
白色
红Ⅰ
红Ⅱ
白色
白色
红Ⅰ
红Ⅰ
红Ⅱ
红Ⅱ
落在白色区域与落在红色区域:可能性不相等
1.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.
1
3
黄2
开始
红
黄1
黄2
(红,黄2)
黄2
红
黄1
红
(黄1,黄2)
(黄1,红)
(黄2,黄1)
(黄2,红)
黄1
(红,黄1)
第一次
第二次
所有可能结果
夯实基础,稳扎稳打
2. 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?
解:设两双袜子分别为A1、A2、B1、B2,则
开始
A1 A2 B 1 B2
A2 B1 B2 A1 B1 B2 A1 A2 B2 A1 A2 B1
√
√
√
√
所以穿相同一双袜子的概率为
第一次
第二次
第一次所选袜子
第二次所选袜子
所有可能结果
A1
A2
B1
B2
A1
A2
B1
B2
(A1,A2)
(A1,B1)
(A1,B2)
(A2,A1)
(A2,B1)
(A2,B2)
(B1,A1)
(B1,A2)
(B1,B2)
(B2,A1)
(B2,A2)
(B2,B1)
用表格求所有可能结果时,你可要特别谨慎哦
4. 小明和小刚玩“石头、剪刀、布”的游戏,每一局游戏双方各自随机做出“石头”、“剪刀”、“布”三种手势的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,相同的手势是和局.
(1)用树形图或列表法计算在一局游戏中两人获胜的概率各是多少?
解:(1)画树状图得:
∵总共有9种情况,每一种出现的机会均等,每人获胜的情形都是3种,
∴两人获胜的概率都是
小明
小刚
5.有一个转盘如图,绿色扇形的圆心角为90°,黄色扇形的圆心角为270°,让转盘自由转动2次,2次指针都落在绿色区域的概率是多少?
90°
黄1
黄2
黄3
第二次
绿
黄1
黄2
黄3
第一次
绿 黄1 黄2 黄3
绿 黄1 黄2 黄3
绿 黄1 黄2 黄3
绿 黄1 黄2 黄3
P(指针两次都落在绿色区域)=
.
6.一书架有上下两层,其中上层有2本语文书1本数学书,下层有2本语文书
2本数学书,现从上下层随机各取1本,求抽到的2本都是数学书的概率。
7. 已知一个口袋中装有7个除颜色外其他无差别的球,其中3个白球,4个黑球.从中随机取出一个球.若往口袋中再放入x个白球和y个黑球,使得取出白球的概率是 ,求y与x之间的函数关系式.
连续递推,豁然开朗
8.校园足球燃激情,绿茵场上展风采.甲、乙、丙三人在练习互相传球,规则是:第一次传球由甲将球随机地传给乙、丙中的某一人,以后的每一次传球都是由持球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在乙手中的概率;
解:画树状图如图:
两次传球后的所有结果有4种,每种结果发生的可能性相等,球恰好在乙手中
(记为事件A)的结果有1种,
(2)求三次传球后,球恰在甲手中的概率.
三次传球后的所有结果有8种,每种结果发生的可能性相等,其中球恰在甲手中
(记为事件B)的结果有2种,
树状图:
第一次传球由甲将球随机地传给乙、丙中的某一人,以后的每一次传球都是由持球者随机地传给其他两人中的某一人.
9.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
