2.4 概率 的简单应用 课件(共21张PPT)
文档属性
| 名称 | 2.4 概率 的简单应用 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
浙教版九年级上册
第二章 简单事件的概率
2. 4 概率的简单应用
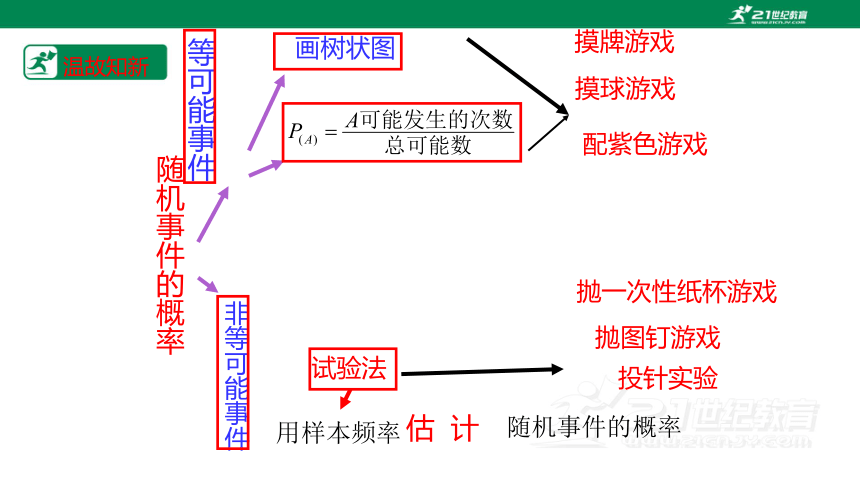
等可能事件
非等可能事件
画树状图
试验法
用样本频率
估 计
随机事件的概率
摸牌游戏
摸球游戏
配紫色游戏
抛一次性纸杯游戏
抛图钉游戏
投针实验
随机事件的概率
温故知新
例1. 某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?
解: 因为10000张奖券中能中一等奖的张数是10张, 所以1张奖券中一等奖的概率是:
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张)
所以1张奖券中奖的概率是
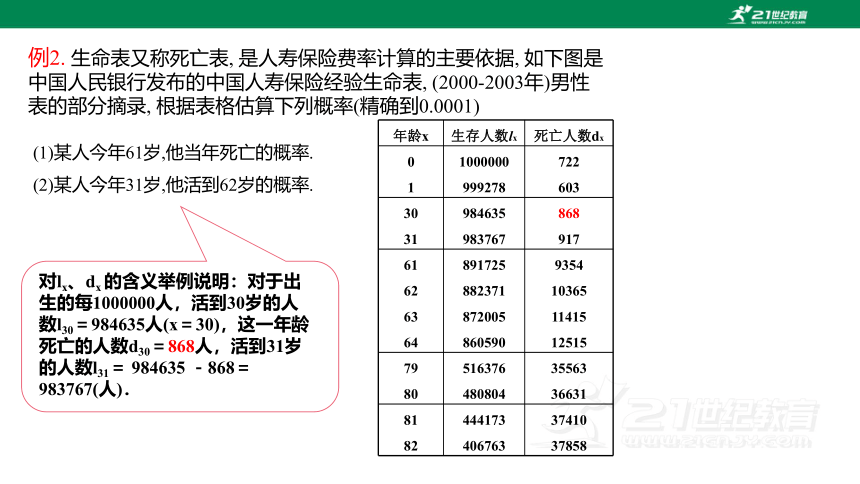
例2. 生命表又称死亡表, 是人寿保险费率计算的主要依据, 如下图是中国人民银行发布的中国人寿保险经验生命表, (2000-2003年)男性表的部分摘录, 根据表格估算下列概率(精确到0.0001)
年龄x 生存人数lx 死亡人数dx
0 1 1000000 999278 722
603
30 31 984635 983767 868
917
61 62 63 64 891725 882371 872005 860590 9354
10365
11415
12515
79 80 516376 480804 35563
36631
81 82 444173 406763 37410
37858
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
对lx、dx 的含义举例说明:对于出生的每1000000人,活到30岁的人数l30=984635人(x=30),这一年龄死亡的人数d30=868人,活到31岁的人数l31= 984635 -868= 983767(人).
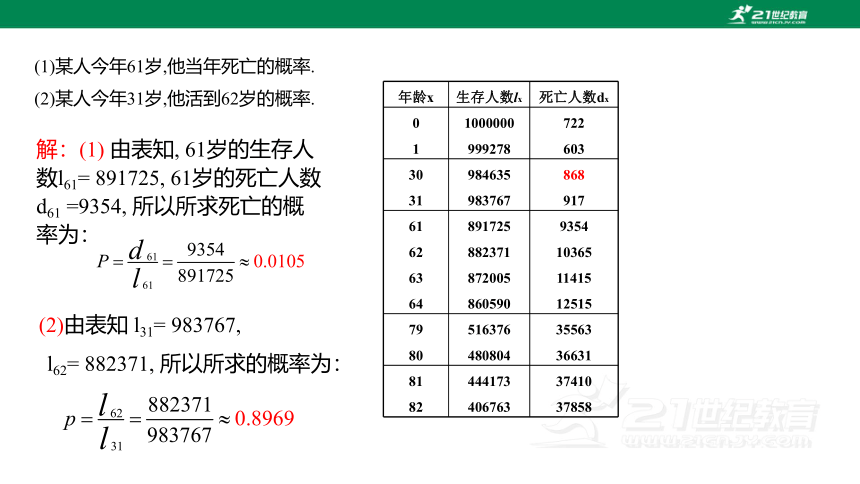
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
解:(1) 由表知, 61岁的生存人数l61= 891725, 61岁的死亡人数d61 =9354, 所以所求死亡的概率为:
(2)由表知 l31= 983767,
l62= 882371, 所以所求的概率为:
年龄x 生存人数lx 死亡人数dx
0 1 1000000 999278 722
603
30 31 984635 983767 868
917
61 62 63 64 891725 882371 872005 860590 9354
10365
11415
12515
79 80 516376 480804 35563
36631
81 82 444173 406763 37410
37858
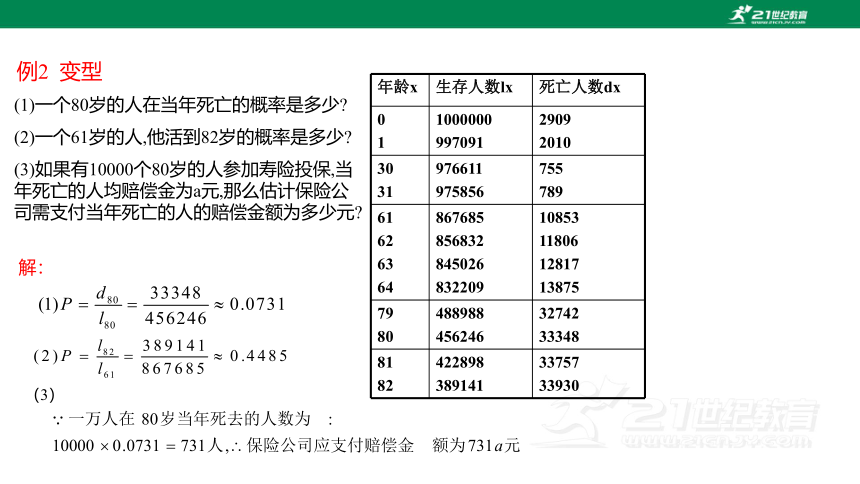
例2 变型
(1)一个80岁的人在当年死亡的概率是多少
(2)一个61岁的人,他活到82岁的概率是多少
(3)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元
年龄x 生存人数lx 死亡人数dx
0 1 1000000 997091 2909
2010
30 31 976611 975856 755
789
61 62 63 64 867685 856832 845026 832209 10853
11806
12817
13875
79 80 488988 456246 32742
33348
81 82 422898 389141 33757
33930
解:
(3)
1. 九年级三班同学作了关于私家车乘坐人数的统计, 在100辆私家车中,统计结果如下表:
每辆私家车乘客数目 1 2 3 4 5
私家车数目 58 27 8 4 3
根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少
夯实基础,稳扎稳打
B
3 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
解:(1)∵共有9种等可能的结果,其中2的倍数有4个,
(2)游戏不公平,
∵共有9种等可能的结果,其中3的倍数有3个,
∴游戏不公平
游戏是否公平的标准:
两者的概率相等,则游戏公平;否则游戏不公平
4.如图所示,一个转盘被平均分成六个扇形,并在上面依次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
(1)指针指向4的概率_____;(直接写出答案)
(2)指针指向数字是奇数的概率____;(直接写出答案)
(3)指针指向数字不小于5的概率_____;(直接写出答案)
(4)现只有一张电影票,小王和小李都想去看,请你利用这个转盘,设计一个公平的游戏规则.
.
(4)自由转动转盘,当它停止转动时,指针指向数字是偶数时小王胜,否则小李胜.
5.九(1)班组织班级联谊会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中数字为“2”“3”“3”“5”“6”的5张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌的数字后放回,完成一次抽奖.记每次抽出2张牌的数字之差为x,按表格要求确定奖项.
奖项 一等奖 二等奖 三等奖
|x| |x|=4 |x|=3 1≤|x|<3
(1)用列表或画树状图的方法求出甲同学抽奖一次获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
连续递推,豁然开朗
解:(1)画树状图如下:
∵共有20种等可能的情况,甲同学抽奖一次获得一等奖的有2种情况,
∴甲同学抽奖一次获得一等奖的概率为 = .
(2)不一定.理由:当抽出的两张牌的数字都是3时,|x|=0,不会获奖.
.
6.把大小和形状完全相同的6张卡片分成两组,每组3张,分别都标上数字1,2,3,将这两组卡片分别放入两个不透明的盒子中摇匀,再从中各随机抽取一张.
(1)请用画树状图或列表的方法求取出的两张卡片上的数字都为奇数的概率;
解:画树状图如下.
由上图可知,所有等可能结果共有9种,其中两张卡片都为奇数的结果有4种,
则取出的两张卡片上的数字都为奇数的概率是
(2)若取出的两张卡片上的数字都为奇数,则甲胜;取出的两张卡片上的数字为一奇一偶,则乙胜.试分析这个游戏是否公平,请说明理由.
取出的两张卡片上的数字为一奇一偶的概率为 ,
因此这个游戏公平.
7、四张大小、质地均相同的卡片上分别标有数字1,2,3,4,现将标有数字的一面朝下扣在桌子上,从中随机抽取一张(不放回),再从桌子上剩下的3张中随机抽取第二张.(1)用画树状图的方法,列出前后两次抽得的卡片上所标数字的所有可能情况;
(2)计算抽得的两张卡片上的数字之积为奇数的概率是多少?
(2)P(积为奇数)=
8.一个密码箱的密码,每个数位上的数都是从0到9的自然数。若要使不知道密码的人一次就拨对密码的概率小于,则密码的位数至少需要多少位?
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
10×10×10=1000
>
至少3位
9
白
蓝
红
黄
绿
蓝
红
10、用如图所示的两个转盘进行配“紫色”游戏,
其概率是多少
第一步
第二步
黄
蓝
红
绿
白
蓝
红
白
蓝
红
白
蓝
红
白
蓝
红
“配紫色”游戏体现了概率模型的思想,
它启示我们:概率是对随机现象的一种数学描述,
它可以帮助我们更好地认识随机现象,
并对生活中的一些不确定情况作出自己的决策.
一红一蓝----------紫色
P(配紫色)=
.
.
11.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级上册
第二章 简单事件的概率
2. 4 概率的简单应用
等可能事件
非等可能事件
画树状图
试验法
用样本频率
估 计
随机事件的概率
摸牌游戏
摸球游戏
配紫色游戏
抛一次性纸杯游戏
抛图钉游戏
投针实验
随机事件的概率
温故知新
例1. 某商场举办有奖销售活动,每张奖券获奖的可能性相同,以每10000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖100个,问1张奖券中一等奖的概率是多少?中奖的概率是多少?
解: 因为10000张奖券中能中一等奖的张数是10张, 所以1张奖券中一等奖的概率是:
又因为10000张奖券中能中奖的奖券总数是1+10+100=111(张)
所以1张奖券中奖的概率是
例2. 生命表又称死亡表, 是人寿保险费率计算的主要依据, 如下图是中国人民银行发布的中国人寿保险经验生命表, (2000-2003年)男性表的部分摘录, 根据表格估算下列概率(精确到0.0001)
年龄x 生存人数lx 死亡人数dx
0 1 1000000 999278 722
603
30 31 984635 983767 868
917
61 62 63 64 891725 882371 872005 860590 9354
10365
11415
12515
79 80 516376 480804 35563
36631
81 82 444173 406763 37410
37858
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
对lx、dx 的含义举例说明:对于出生的每1000000人,活到30岁的人数l30=984635人(x=30),这一年龄死亡的人数d30=868人,活到31岁的人数l31= 984635 -868= 983767(人).
(1)某人今年61岁,他当年死亡的概率.
(2)某人今年31岁,他活到62岁的概率.
解:(1) 由表知, 61岁的生存人数l61= 891725, 61岁的死亡人数d61 =9354, 所以所求死亡的概率为:
(2)由表知 l31= 983767,
l62= 882371, 所以所求的概率为:
年龄x 生存人数lx 死亡人数dx
0 1 1000000 999278 722
603
30 31 984635 983767 868
917
61 62 63 64 891725 882371 872005 860590 9354
10365
11415
12515
79 80 516376 480804 35563
36631
81 82 444173 406763 37410
37858
例2 变型
(1)一个80岁的人在当年死亡的概率是多少
(2)一个61岁的人,他活到82岁的概率是多少
(3)如果有10000个80岁的人参加寿险投保,当年死亡的人均赔偿金为a元,那么估计保险公司需支付当年死亡的人的赔偿金额为多少元
年龄x 生存人数lx 死亡人数dx
0 1 1000000 997091 2909
2010
30 31 976611 975856 755
789
61 62 63 64 867685 856832 845026 832209 10853
11806
12817
13875
79 80 488988 456246 32742
33348
81 82 422898 389141 33757
33930
解:
(3)
1. 九年级三班同学作了关于私家车乘坐人数的统计, 在100辆私家车中,统计结果如下表:
每辆私家车乘客数目 1 2 3 4 5
私家车数目 58 27 8 4 3
根据以上结果,估计抽查一辆私家车而它载有超过2名乘客的概率是多少
夯实基础,稳扎稳打
B
3 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
(1)转盘转到2的倍数的概率是多少?
(2)你认为这个游戏公平吗?请说明理由.
解:(1)∵共有9种等可能的结果,其中2的倍数有4个,
(2)游戏不公平,
∵共有9种等可能的结果,其中3的倍数有3个,
∴游戏不公平
游戏是否公平的标准:
两者的概率相等,则游戏公平;否则游戏不公平
4.如图所示,一个转盘被平均分成六个扇形,并在上面依次写上数字1、2、3、4、5、6;若自由转动转盘,当它停止转动时,求:
(1)指针指向4的概率_____;(直接写出答案)
(2)指针指向数字是奇数的概率____;(直接写出答案)
(3)指针指向数字不小于5的概率_____;(直接写出答案)
(4)现只有一张电影票,小王和小李都想去看,请你利用这个转盘,设计一个公平的游戏规则.
.
(4)自由转动转盘,当它停止转动时,指针指向数字是偶数时小王胜,否则小李胜.
5.九(1)班组织班级联谊会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中数字为“2”“3”“3”“5”“6”的5张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌的数字后放回,完成一次抽奖.记每次抽出2张牌的数字之差为x,按表格要求确定奖项.
奖项 一等奖 二等奖 三等奖
|x| |x|=4 |x|=3 1≤|x|<3
(1)用列表或画树状图的方法求出甲同学抽奖一次获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
连续递推,豁然开朗
解:(1)画树状图如下:
∵共有20种等可能的情况,甲同学抽奖一次获得一等奖的有2种情况,
∴甲同学抽奖一次获得一等奖的概率为 = .
(2)不一定.理由:当抽出的两张牌的数字都是3时,|x|=0,不会获奖.
.
6.把大小和形状完全相同的6张卡片分成两组,每组3张,分别都标上数字1,2,3,将这两组卡片分别放入两个不透明的盒子中摇匀,再从中各随机抽取一张.
(1)请用画树状图或列表的方法求取出的两张卡片上的数字都为奇数的概率;
解:画树状图如下.
由上图可知,所有等可能结果共有9种,其中两张卡片都为奇数的结果有4种,
则取出的两张卡片上的数字都为奇数的概率是
(2)若取出的两张卡片上的数字都为奇数,则甲胜;取出的两张卡片上的数字为一奇一偶,则乙胜.试分析这个游戏是否公平,请说明理由.
取出的两张卡片上的数字为一奇一偶的概率为 ,
因此这个游戏公平.
7、四张大小、质地均相同的卡片上分别标有数字1,2,3,4,现将标有数字的一面朝下扣在桌子上,从中随机抽取一张(不放回),再从桌子上剩下的3张中随机抽取第二张.(1)用画树状图的方法,列出前后两次抽得的卡片上所标数字的所有可能情况;
(2)计算抽得的两张卡片上的数字之积为奇数的概率是多少?
(2)P(积为奇数)=
8.一个密码箱的密码,每个数位上的数都是从0到9的自然数。若要使不知道密码的人一次就拨对密码的概率小于,则密码的位数至少需要多少位?
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
10×10×10=1000
>
至少3位
9
白
蓝
红
黄
绿
蓝
红
10、用如图所示的两个转盘进行配“紫色”游戏,
其概率是多少
第一步
第二步
黄
蓝
红
绿
白
蓝
红
白
蓝
红
白
蓝
红
白
蓝
红
“配紫色”游戏体现了概率模型的思想,
它启示我们:概率是对随机现象的一种数学描述,
它可以帮助我们更好地认识随机现象,
并对生活中的一些不确定情况作出自己的决策.
一红一蓝----------紫色
P(配紫色)=
.
.
11.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
