５．１多边形３(浙江省温州市瑞安市)

课件27张PPT。5.1多边形（3）n边形的内角和为(n－2) ×180°(n≥3)n边形从一个顶点出发的对角线有(n－3)条(n≥3)任何多边形的外角和为360°回顾：四边形的内角和、外角和有哪些性质？
四边形的内角和等于360°。四边形的外角和等于360°多边形对角线内角和、外角和有哪些性质？练一练:（2）已知一个多边形的内角和为720o ，则这个多边形是______边形6（1）八边形的内角和为______，外角和为_____1080360o（3）已知一个多边形的每一个外角都是72o，求这个边形的边数为______5（4）在五边形ABCDE中，若∠A=∠D=90o,且 ∠B:∠C:∠E=3:2:4,则∠C的度数为_______80o它们有什么共同特征呢？ 各边相等,各角也相等定 义我们把的多边形叫做正多边形三个角相等的三角形是正三角形吗？
三条边相等的三角形是正三角形吗？
四个角相等的四边形呢？
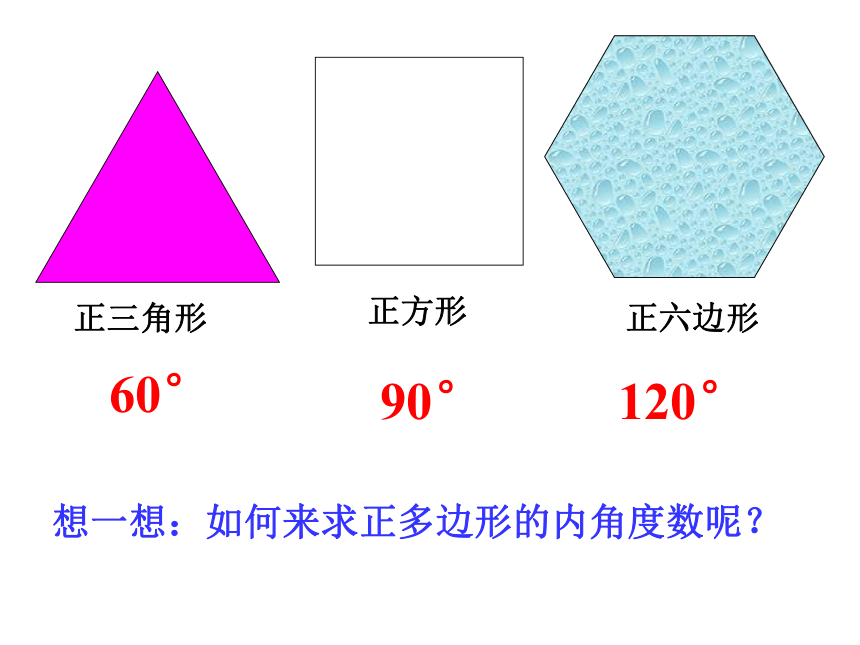
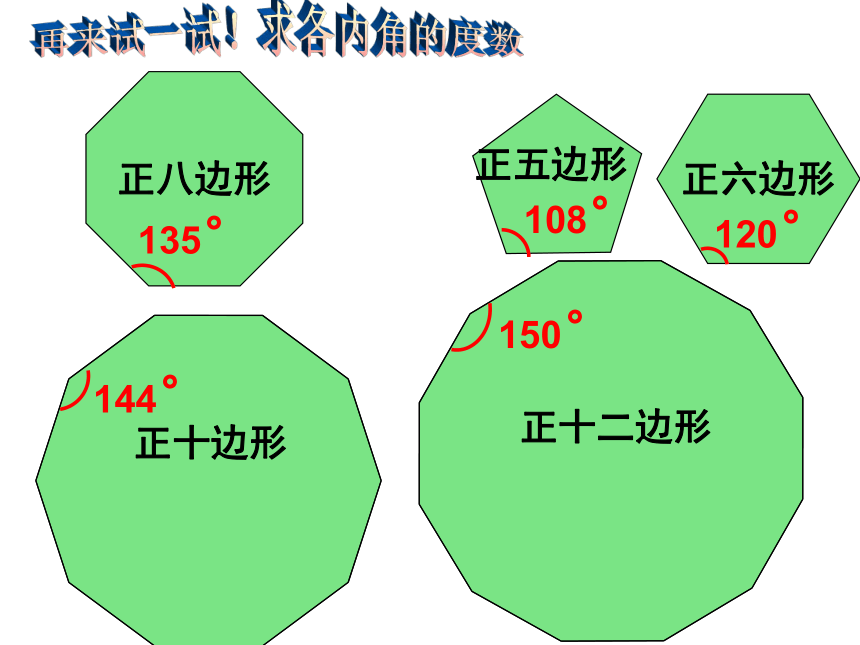
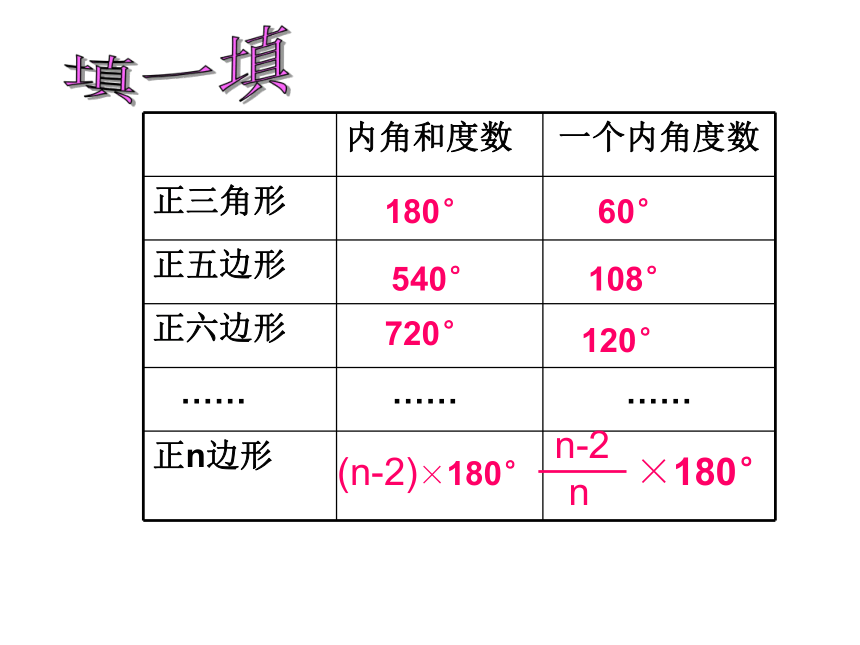
四条边相等的四边形呢？思考：正三角形正方形正六边形想一想：如何来求正多边形的内角度数呢？60°90°120°再来试一试！求各内角的度数正六边形正八边形正十边形正十二边形正五边形180°60°540°108°720°120°(n-2)×180°×180°填一填 正五边形、正八边形、都是轴对称图形吗？它们各有几条对称轴？一起欣赏◇ 由于正多边形有许多优良的性质，匀称美观，常被人们用于图案设计和镶嵌平面.镶嵌用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。图（1）图（2）图（3）有空隙有重叠 你能用一些全等的正三角形单独镶嵌成平面图案吗？探究活动一正方形、正五边形、正六边形也可以单独镶嵌吗？做一做，试试看.探究活动一拼不了啦,为什么呢?你能说说道理吗?123∠1+∠2+∠3=324°60°K=6能拼好90°K=4能拼好108°K=3不能拼好,
有缺口108°K=4不能拼好,
有重叠120°K=3能拼好 观察并指出在每个图案中,正多边形必须
具备下列条件:
1)边长_____,
2)顶点______,
3)在一个顶点处_________________________相等公用各多边形的内角之和为360度正六边形正八边形正十边形正十二边形正五边形(1)要用一种正多边形镶嵌,这个多边形的每个内角度数能整除360o仅用一种正多边形镶嵌，只有正三角形、正方形、正六边形能镶嵌成一个平面吗？再创情景 拓展探究 　　用两种正多边形镶嵌,哪些能镶嵌成一个平面?各用几个呢?需要满足什么条件呢?探究问题（二）一起欣赏 多种正边形镶嵌平面.试一试用边长相等的正三角形和正六边形能不能镶嵌呢？正六边形正六边形正六边形（1）、用边长相等的正四角形和正八边形能不能镶嵌呢？（2）、用边长相等的正五角形和正十边形能不能镶嵌呢？课外思考题！做一做（1）任意剪出一些形状、大小完全相同的三角形纸板,拼拼看,它们能否镶嵌成平面图案.（2）任意剪出一些形状、大小完全相同的四边形纸板,
拼拼看,它们能否镶嵌成平面图案.
课 堂 小 结 通过本节课的学习，你学到了什么？有什么收获呢？让我们一起回顾与分享吧！ 1、平面镶嵌的两个条件：不重叠，无空隙.
2、一种正多边形的镶嵌：
只有三种：正三角形、正四边形、正六边形
规律：正多边形的内角一定是360°的约数
3、两种正多边形的镶嵌：
规律：拼接在同一个点的各个角的和等于360°.