1.1 锐角三角函数 (1) 课件(共29张PPT)
文档属性
| 名称 | 1.1 锐角三角函数 (1) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-30 00:00:00 | ||
图片预览



文档简介
(共29张PPT)
浙教版九年级下册
1.1 锐角三角函数 (1)
第一章 解直角三角形
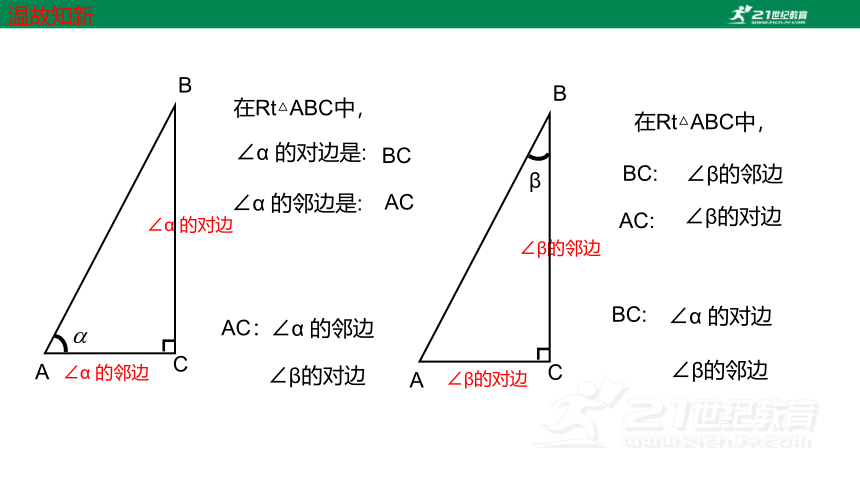
∠α 的对边是:
在Rt△ABC中,
A
B
C
┗
BC
∠α 的对边
∠α 的邻边是:
AC
∠α 的邻边
在Rt△ABC中,
BC:
∠β的邻边
∠β的邻边
A
B
C
┗
β
AC:
∠β的对边
∠β的对边
AC:
∠α 的邻边
∠β的对边
BC:
∠α 的对边
∠β的邻边
温故知新
A
B
C
B1
C1
┗
┗
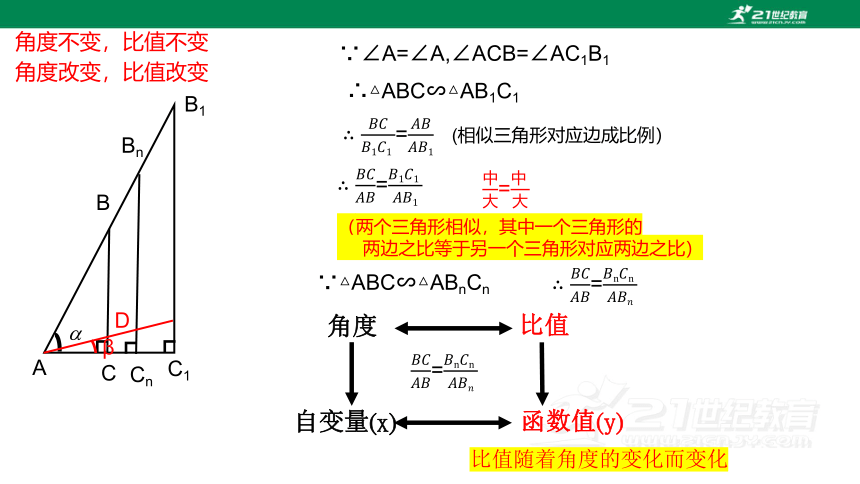
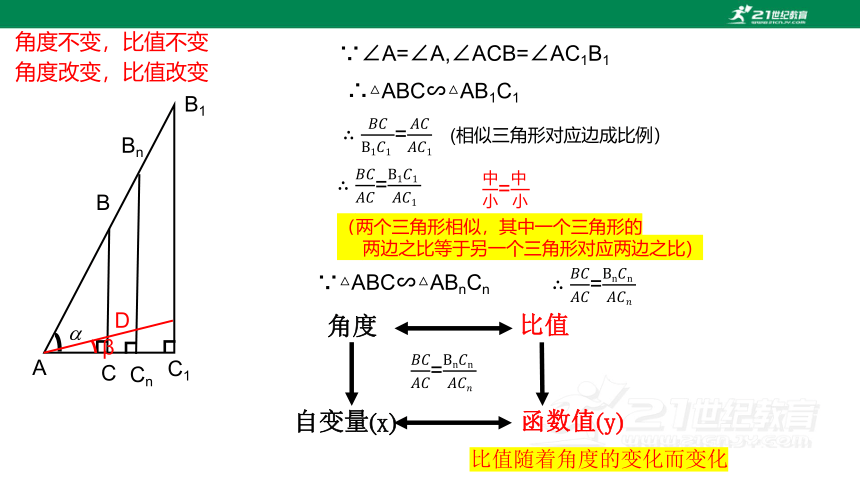
∵∠A=∠A,∠ACB=∠AC1B1
∴△ABC∽△AB1C1
=
= (相似三角形对应边成比例)
(两个三角形相似,其中一个三角形的
两边之比等于另一个三角形对应两边之比)
=
Bn
Cn
┗
∵△ABC∽△ABnCn
=
角度
角度不变,比值不变
比值
角度改变,比值改变
=
β
自变量(x)
函数值(y)
比值随着角度的变化而变化
D
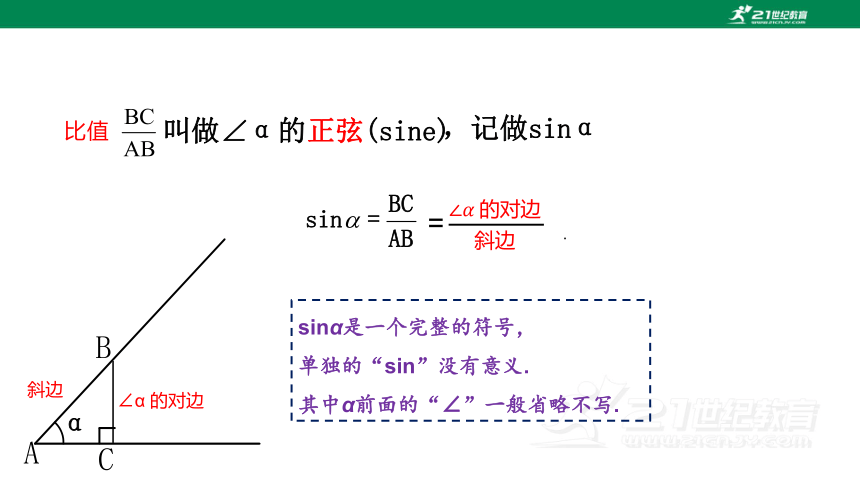
比值
叫做∠α的正弦(sine)
,记做sinα
A
α
B
C
sinα是一个完整的符号,
单独的“sin”没有意义.
其中α前面的“∠”一般省略不写.
∠α 的对边
斜边
=
.
A
B
C
B1
C1
┗
┗
∵∠A=∠A,∠ACB=∠AC1B1
∴△ABC∽△AB1C1
=
= (相似三角形对应边成比例)
(两个三角形相似,其中一个三角形的
两边之比等于另一个三角形对应两边之比)
=
Bn
Cn
┗
∵△ABC∽△ABnCn
=
角度
角度不变,比值不变
比值
角度改变,比值改变
=
β
自变量(x)
函数值(y)
比值随着角度的变化而变化
D
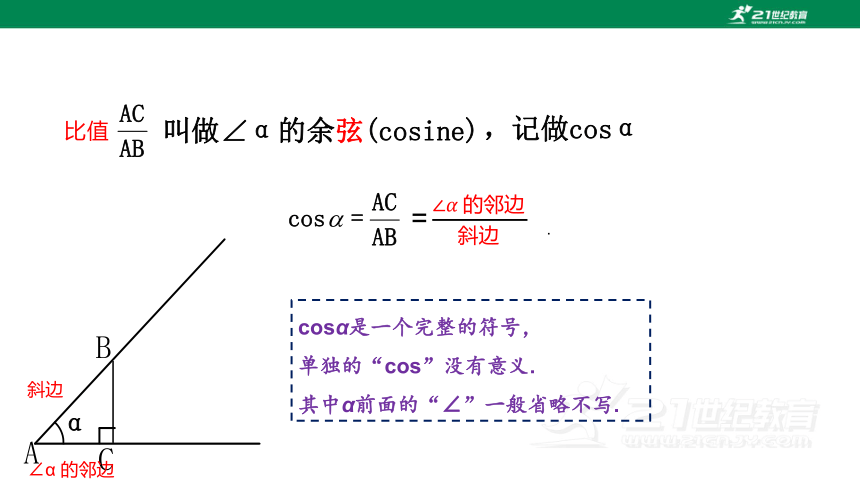
比值
叫做∠α的余弦(cosine)
,记做cosα
A
α
B
C
cosα是一个完整的符号,
单独的“cos”没有意义.
其中α前面的“∠”一般省略不写.
∠α 的邻边
斜边
=
.
A
B
C
B1
C1
┗
┗
∵∠A=∠A,∠ACB=∠AC1B1
∴△ABC∽△AB1C1
=
= (相似三角形对应边成比例)
(两个三角形相似,其中一个三角形的
两边之比等于另一个三角形对应两边之比)
=
Bn
Cn
┗
∵△ABC∽△ABnCn
=
角度
角度不变,比值不变
比值
角度改变,比值改变
=
β
自变量(x)
函数值(y)
比值随着角度的变化而变化
D
比值
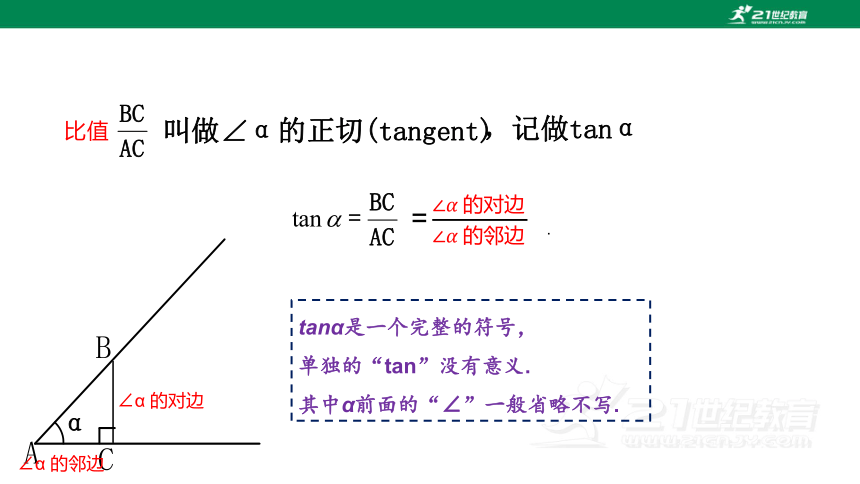
叫做∠α的正切(tangent)
,记做tanα
A
α
B
C
tanα是一个完整的符号,
单独的“tan”没有意义.
其中α前面的“∠”一般省略不写.
∠α 的对边
∠α 的邻边
=
.
A
C
B
一般地,对于每一个确定的锐角α,在角的一边上任取一点B,作BC⊥AC于点C,
都是一个确定的值,与点B在角的边上的位置无关。
都是锐角α的三角函数。
比值
C
B
A
比值
,叫做∠α的正弦
比值
,叫做∠α的余弦
比值
,叫做∠α的正切
记做:sinα
记做:cosα
记做:tanα
定义:
如图,在Rt△ABC中,∠C=Rt∠
A
B
C
∠A的对边
∠A的邻边
斜边
锐角α的正弦、余弦、正切统称为∠α的三角函数
1.作一个30°的∠A,在角的边上任意取一点B,
作BC⊥AC于点C.计算300的的正弦,余弦和正切值.
.
A
B
C
30°
= ,
.
,
.
=.
.
2. 如图,在Rt△ABC中,∠C=Rt∠,AB=5,BC=3.
求∠A的正弦,余弦和正切.
A
B
C
∴ sinA= = , cosA= = ,tanA= = .
.
解:如图,在Rt△ABC中,AB=5,BC=3,
∴AC=4.
.
α
3.已知∠α,根据三角函数的定义求sinα,cosα,tanα.
┗
a
b
c
sinα=
cosα=
tanα=
1. 如图,在Rt△ABC中,∠A=90°.
则∠B的对边是 ;
∠B的邻边是 ;
∠C的对边是 ;
∠C的邻边是 .
A
B
C
AC
AB
AB
AC
夯实基础,稳扎稳打
2.对于每一个确定的锐角α,在角一边上任取一点B,
作BC⊥AC于点C,如图所示,
3、如图,把Rt△ABC的三边的长度都扩大为原来的3倍,则∠A的正弦值( )
A、不变 B、缩小为原来的
C、扩大为原来的 D、不能确定
A
B
C
A
4、如右图,∠ACB=90°,CD⊥AB,AC=5,CD=3.
则sin∠ACD=_____=_____,cos∠ACD=_____=_____,
sinA=_____=_____,cosA=_____=_____.
┍
┌
A
C
B
D
.
.
.
.
.
.
.
.
5.如图,在Rt△ABC中,∠C=90°, AC=2,BC=3,求:
(1)sin A ,cos B;
A
B
C
(2)cos A ,sin B;
(3)观察(1)(2)计算结果,你发现了什么?
由于∠A+∠B=90°
∠A的对边就是∠B的邻边
∠A的邻边就是∠B的对边
6.小明在解决某一数学问题时,算得sinA= ,
你觉得他算的对吗?为什么?
.
分析:不对. 因为sinA= =<1, >1 ,
所以小明计算错误.
.
锐角三角函数的值都是正实数,并且0< sinα <1, 0< cosα <1.
A
B
C
连续递推,豁然开朗
斜大于直
7.如图所示,△ABC的三个顶点分别在正方形网格的格点上,则tan A的值是 ( )
A
∟
8.如图,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6,AC=8,则sin ∠ABD的值是 ( )
D
∟
∟
.
.
10、在等腰三角形ABC中, AB =AC =5,BC=6,求sinB,cosB,tanB.
解:如右图,作BC边上的高AD,则BD=CD.
∵ BC=6,∴ BD=CD=3.
又∵ AB =AC =5,∴ AD== 4.
∴ sinB==,cosB== ,tanB==.
A
B
C
D
∟
11.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是 .
∟
13.如图, ∠C=90°,CD⊥AB.
┍
┌
A
C
B
D
CD
BC
AC
AB
AD
AC
14.
tanα=
.
tanα'=
.
tanα的值可以大于100
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级下册
1.1 锐角三角函数 (1)
第一章 解直角三角形
∠α 的对边是:
在Rt△ABC中,
A
B
C
┗
BC
∠α 的对边
∠α 的邻边是:
AC
∠α 的邻边
在Rt△ABC中,
BC:
∠β的邻边
∠β的邻边
A
B
C
┗
β
AC:
∠β的对边
∠β的对边
AC:
∠α 的邻边
∠β的对边
BC:
∠α 的对边
∠β的邻边
温故知新
A
B
C
B1
C1
┗
┗
∵∠A=∠A,∠ACB=∠AC1B1
∴△ABC∽△AB1C1
=
= (相似三角形对应边成比例)
(两个三角形相似,其中一个三角形的
两边之比等于另一个三角形对应两边之比)
=
Bn
Cn
┗
∵△ABC∽△ABnCn
=
角度
角度不变,比值不变
比值
角度改变,比值改变
=
β
自变量(x)
函数值(y)
比值随着角度的变化而变化
D
比值
叫做∠α的正弦(sine)
,记做sinα
A
α
B
C
sinα是一个完整的符号,
单独的“sin”没有意义.
其中α前面的“∠”一般省略不写.
∠α 的对边
斜边
=
.
A
B
C
B1
C1
┗
┗
∵∠A=∠A,∠ACB=∠AC1B1
∴△ABC∽△AB1C1
=
= (相似三角形对应边成比例)
(两个三角形相似,其中一个三角形的
两边之比等于另一个三角形对应两边之比)
=
Bn
Cn
┗
∵△ABC∽△ABnCn
=
角度
角度不变,比值不变
比值
角度改变,比值改变
=
β
自变量(x)
函数值(y)
比值随着角度的变化而变化
D
比值
叫做∠α的余弦(cosine)
,记做cosα
A
α
B
C
cosα是一个完整的符号,
单独的“cos”没有意义.
其中α前面的“∠”一般省略不写.
∠α 的邻边
斜边
=
.
A
B
C
B1
C1
┗
┗
∵∠A=∠A,∠ACB=∠AC1B1
∴△ABC∽△AB1C1
=
= (相似三角形对应边成比例)
(两个三角形相似,其中一个三角形的
两边之比等于另一个三角形对应两边之比)
=
Bn
Cn
┗
∵△ABC∽△ABnCn
=
角度
角度不变,比值不变
比值
角度改变,比值改变
=
β
自变量(x)
函数值(y)
比值随着角度的变化而变化
D
比值
叫做∠α的正切(tangent)
,记做tanα
A
α
B
C
tanα是一个完整的符号,
单独的“tan”没有意义.
其中α前面的“∠”一般省略不写.
∠α 的对边
∠α 的邻边
=
.
A
C
B
一般地,对于每一个确定的锐角α,在角的一边上任取一点B,作BC⊥AC于点C,
都是一个确定的值,与点B在角的边上的位置无关。
都是锐角α的三角函数。
比值
C
B
A
比值
,叫做∠α的正弦
比值
,叫做∠α的余弦
比值
,叫做∠α的正切
记做:sinα
记做:cosα
记做:tanα
定义:
如图,在Rt△ABC中,∠C=Rt∠
A
B
C
∠A的对边
∠A的邻边
斜边
锐角α的正弦、余弦、正切统称为∠α的三角函数
1.作一个30°的∠A,在角的边上任意取一点B,
作BC⊥AC于点C.计算300的的正弦,余弦和正切值.
.
A
B
C
30°
= ,
.
,
.
=.
.
2. 如图,在Rt△ABC中,∠C=Rt∠,AB=5,BC=3.
求∠A的正弦,余弦和正切.
A
B
C
∴ sinA= = , cosA= = ,tanA= = .
.
解:如图,在Rt△ABC中,AB=5,BC=3,
∴AC=4.
.
α
3.已知∠α,根据三角函数的定义求sinα,cosα,tanα.
┗
a
b
c
sinα=
cosα=
tanα=
1. 如图,在Rt△ABC中,∠A=90°.
则∠B的对边是 ;
∠B的邻边是 ;
∠C的对边是 ;
∠C的邻边是 .
A
B
C
AC
AB
AB
AC
夯实基础,稳扎稳打
2.对于每一个确定的锐角α,在角一边上任取一点B,
作BC⊥AC于点C,如图所示,
3、如图,把Rt△ABC的三边的长度都扩大为原来的3倍,则∠A的正弦值( )
A、不变 B、缩小为原来的
C、扩大为原来的 D、不能确定
A
B
C
A
4、如右图,∠ACB=90°,CD⊥AB,AC=5,CD=3.
则sin∠ACD=_____=_____,cos∠ACD=_____=_____,
sinA=_____=_____,cosA=_____=_____.
┍
┌
A
C
B
D
.
.
.
.
.
.
.
.
5.如图,在Rt△ABC中,∠C=90°, AC=2,BC=3,求:
(1)sin A ,cos B;
A
B
C
(2)cos A ,sin B;
(3)观察(1)(2)计算结果,你发现了什么?
由于∠A+∠B=90°
∠A的对边就是∠B的邻边
∠A的邻边就是∠B的对边
6.小明在解决某一数学问题时,算得sinA= ,
你觉得他算的对吗?为什么?
.
分析:不对. 因为sinA= =<1, >1 ,
所以小明计算错误.
.
锐角三角函数的值都是正实数,并且0< sinα <1, 0< cosα <1.
A
B
C
连续递推,豁然开朗
斜大于直
7.如图所示,△ABC的三个顶点分别在正方形网格的格点上,则tan A的值是 ( )
A
∟
8.如图,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6,AC=8,则sin ∠ABD的值是 ( )
D
∟
∟
.
.
10、在等腰三角形ABC中, AB =AC =5,BC=6,求sinB,cosB,tanB.
解:如右图,作BC边上的高AD,则BD=CD.
∵ BC=6,∴ BD=CD=3.
又∵ AB =AC =5,∴ AD== 4.
∴ sinB==,cosB== ,tanB==.
A
B
C
D
∟
11.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是 .
∟
13.如图, ∠C=90°,CD⊥AB.
┍
┌
A
C
B
D
CD
BC
AC
AB
AD
AC
14.
tanα=
.
tanα'=
.
tanα的值可以大于100
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
