1.1 锐角三角函数 (2) 课件(共24张PPT)
文档属性
| 名称 | 1.1 锐角三角函数 (2) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
浙教版九年级下册
1.1 锐角三角函数 (2)
第一章 解直角三角形
在 中,
∠A的正弦:
∠A的余弦 :
温故知新
A
B
C
a
b
c
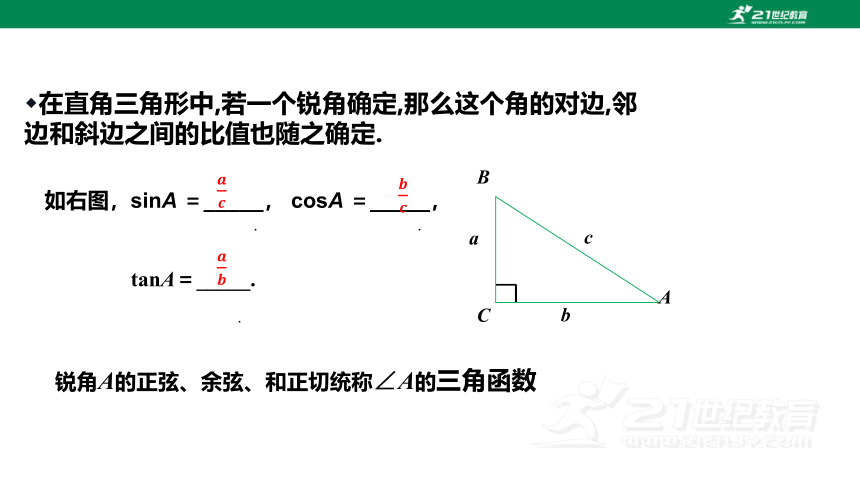
如右图,sinA =_____, cosA =_____,
tanA=_____.
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
锐角A的正弦、余弦、和正切统称∠A的三角函数
.
.
.
A
B
C
30°
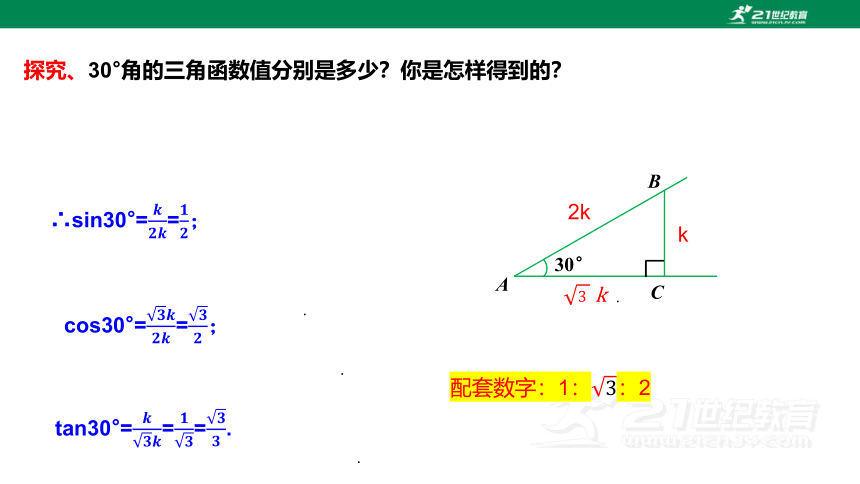
∴sin30°==;
.
cos30°==;
.
tan30°===.
.
探究、30°角的三角函数值分别是多少?你是怎样得到的?
配套数字:1::2
k
k
.
2k
A
B
C
60°
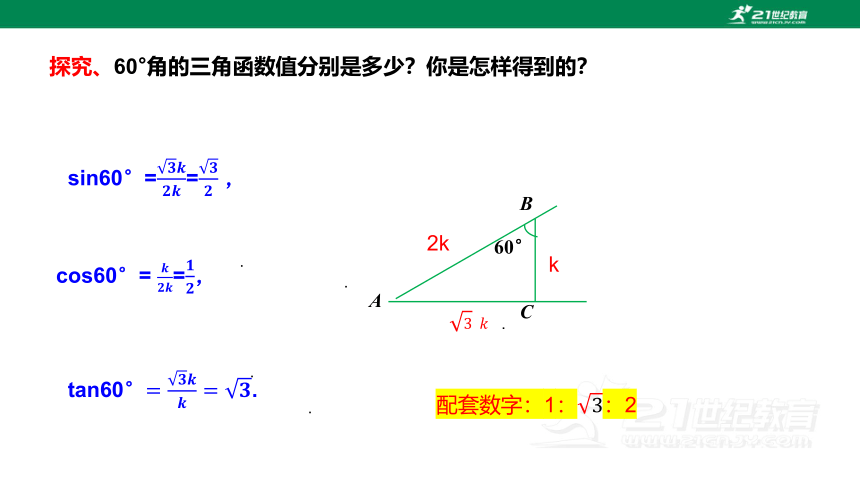
探究、60°角的三角函数值分别是多少?你是怎样得到的?
配套数字:1::2
k
.
2k
sin60°== ,
.
cos60°= =,
.
tan60°.
.
.
45°
A
B
C
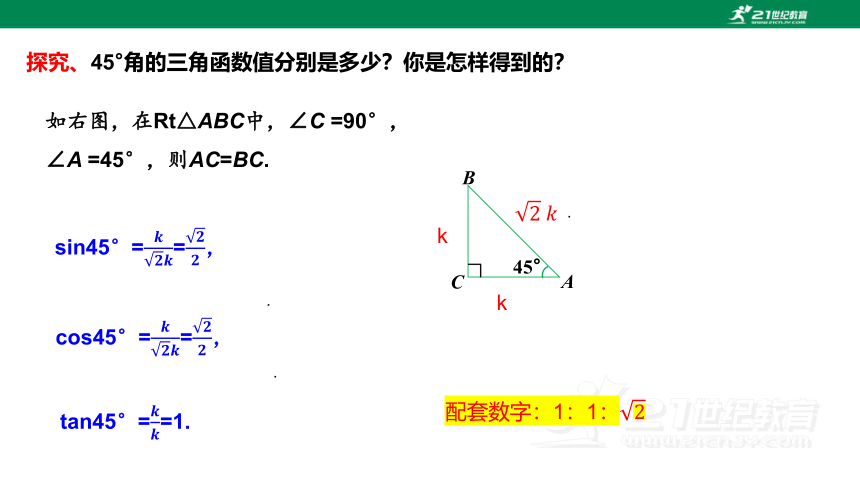
探究、45°角的三角函数值分别是多少?你是怎样得到的?
如右图,在Rt△ABC中,∠C =90°,
∠A =45°,则AC=BC.
sin45°==,
.
cos45°==,
.
tan45°==1.
.
配套数字:1:1:
k
k
.
.
.
.
.
.
.
.
1
.
.
.
A
B
C
30°
配套数字:1::2
1
.
2
45°
A
B
C
配套数字:1:1:
1
1
.
.
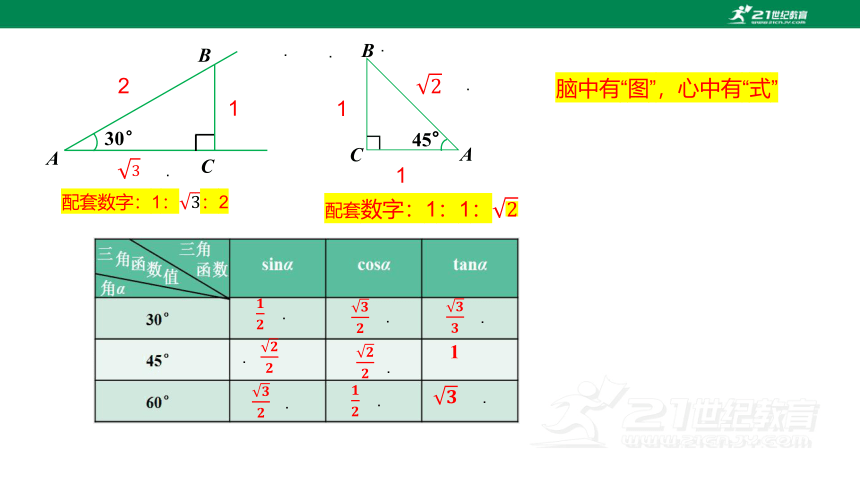
脑中有“图”,心中有“式”
cos245° 表示(cos45°)2.
例2 求下列各式的值:
(1)2sin30°-3cos60°;
(2)cos245°+tan60°sin60°;
(3)cos30° -sin45° + tan45°cos60°.
.
解:(1)2sin30°-3cos60°=2× -3×= - .
.
(2)cos 45°+tan60°sin60°= +×=2.
.
(3) cos30°-sin45°+tan45°cos60°
=× -× +1×=1.
.
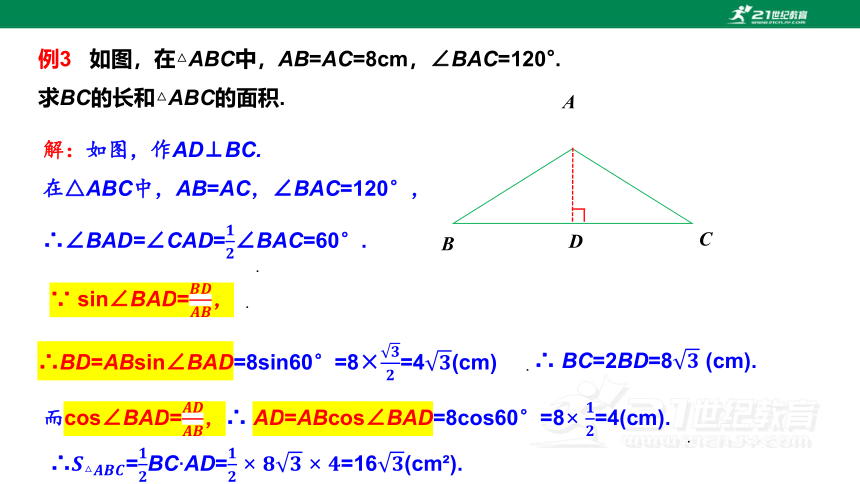
例3 如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
C
B
A
D
解:如图,作AD⊥BC.
在△ABC中,AB=AC,∠BAC=120°,
∴∠BAD=∠CAD=∠BAC=60°.
.
∵ sin∠BAD=,
.
∴BD=ABsin∠BAD=8sin60°=8×=4(cm)
.
∴ BC=2BD=8 (cm).
.
而cos∠BAD=,∴ AD=ABcos∠BAD=8cos60°=8=4(cm).
.
∴=BCAD==16(cm ).
.
A
B
C
30°
1
2
sin30 °=
cos30 °=
tan30 °=
2
3
脑中有“图”,心中有“式”
归纳总结
A
B
C
45°
sin45 °=
cos45°=
tan45°=
2
2
1
1
1
脑中有“图”,心中有“式”
A
C
B
60°
sin60°=
cos60°=
tan60°=
1
2
2
特殊角的三角函数值表
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
(1)当 时,α的正弦值随着角度的增大而增大,
(2)当 时, α的余弦值随着角度的增大而减小,
(3)当 时,α的正切值随着角度的增大而增大,
夯实基础,稳扎稳打
B
2.令a=sin 60°,b=cos 45°,c=tan 30°,则它们之间的大小关系是 ( )
A.c<b<a B.b<a<c
C.a<c<b D.b<c<a
A
∟
A
6
6tan300
.
100sin300
100
100cos300
线段的三角函数表示:
5.计算下列各式的值.
=
.
=
.
=()2 - 2××
.
= -
.
(3)
=()2+()2
.
sin2300+cos2300
=1
6.求下列各式的值:
(1)cos260°+sin260°
(2)
解: (1) cos260°+sin260°
=1
(2)
=0
7.求下列各式的值:
(1)1-2 sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3)
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
脑中有“图”,心中有“式”
8.计算与tan30°,与tan60°,你发现了什么?对于任意锐角α,是否都有=tanα?
.
解:= = =tan30°,= = = tan60°.
.
对于任意锐角α,都有=tanα成立.
.
α
┗
a
b
c
sinα=
.
cosα=
.
.
.
=tanα
.
连续递推,豁然开朗
9.计算下列各式:
(1) sin2450+cos2450
(2) sin2600+cos2600
你发现了什么?对于任意锐角α,是否都有sin2α+cos2α=1 请说明理由
=(
.
=
.
=(
.
=
.
α
┗
a
b
c
sinα=
.
cosα=
.
sin2α+cos2α=
=(
.
=
.
=1
=
.
10. 如图,在△ABC中,∠A=300,
求AB。
A
B
C
D
解:过点C作CD⊥AB于点D
∠A=300,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级下册
1.1 锐角三角函数 (2)
第一章 解直角三角形
在 中,
∠A的正弦:
∠A的余弦 :
温故知新
A
B
C
a
b
c
如右图,sinA =_____, cosA =_____,
tanA=_____.
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
锐角A的正弦、余弦、和正切统称∠A的三角函数
.
.
.
A
B
C
30°
∴sin30°==;
.
cos30°==;
.
tan30°===.
.
探究、30°角的三角函数值分别是多少?你是怎样得到的?
配套数字:1::2
k
k
.
2k
A
B
C
60°
探究、60°角的三角函数值分别是多少?你是怎样得到的?
配套数字:1::2
k
.
2k
sin60°== ,
.
cos60°= =,
.
tan60°.
.
.
45°
A
B
C
探究、45°角的三角函数值分别是多少?你是怎样得到的?
如右图,在Rt△ABC中,∠C =90°,
∠A =45°,则AC=BC.
sin45°==,
.
cos45°==,
.
tan45°==1.
.
配套数字:1:1:
k
k
.
.
.
.
.
.
.
.
1
.
.
.
A
B
C
30°
配套数字:1::2
1
.
2
45°
A
B
C
配套数字:1:1:
1
1
.
.
脑中有“图”,心中有“式”
cos245° 表示(cos45°)2.
例2 求下列各式的值:
(1)2sin30°-3cos60°;
(2)cos245°+tan60°sin60°;
(3)cos30° -sin45° + tan45°cos60°.
.
解:(1)2sin30°-3cos60°=2× -3×= - .
.
(2)cos 45°+tan60°sin60°= +×=2.
.
(3) cos30°-sin45°+tan45°cos60°
=× -× +1×=1.
.
例3 如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
求BC的长和△ABC的面积.
C
B
A
D
解:如图,作AD⊥BC.
在△ABC中,AB=AC,∠BAC=120°,
∴∠BAD=∠CAD=∠BAC=60°.
.
∵ sin∠BAD=,
.
∴BD=ABsin∠BAD=8sin60°=8×=4(cm)
.
∴ BC=2BD=8 (cm).
.
而cos∠BAD=,∴ AD=ABcos∠BAD=8cos60°=8=4(cm).
.
∴=BCAD==16(cm ).
.
A
B
C
30°
1
2
sin30 °=
cos30 °=
tan30 °=
2
3
脑中有“图”,心中有“式”
归纳总结
A
B
C
45°
sin45 °=
cos45°=
tan45°=
2
2
1
1
1
脑中有“图”,心中有“式”
A
C
B
60°
sin60°=
cos60°=
tan60°=
1
2
2
特殊角的三角函数值表
三角函数 锐角α 正弦sinα 余弦cosα 正切tanα
30°
45°
60°
(1)当 时,α的正弦值随着角度的增大而增大,
(2)当 时, α的余弦值随着角度的增大而减小,
(3)当 时,α的正切值随着角度的增大而增大,
夯实基础,稳扎稳打
B
2.令a=sin 60°,b=cos 45°,c=tan 30°,则它们之间的大小关系是 ( )
A.c<b<a B.b<a<c
C.a<c<b D.b<c<a
A
∟
A
6
6tan300
.
100sin300
100
100cos300
线段的三角函数表示:
5.计算下列各式的值.
=
.
=
.
=()2 - 2××
.
= -
.
(3)
=()2+()2
.
sin2300+cos2300
=1
6.求下列各式的值:
(1)cos260°+sin260°
(2)
解: (1) cos260°+sin260°
=1
(2)
=0
7.求下列各式的值:
(1)1-2 sin30°cos30° (2)3tan30°-tan45°+2sin60°
(3)
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
脑中有“图”,心中有“式”
8.计算与tan30°,与tan60°,你发现了什么?对于任意锐角α,是否都有=tanα?
.
解:= = =tan30°,= = = tan60°.
.
对于任意锐角α,都有=tanα成立.
.
α
┗
a
b
c
sinα=
.
cosα=
.
.
.
=tanα
.
连续递推,豁然开朗
9.计算下列各式:
(1) sin2450+cos2450
(2) sin2600+cos2600
你发现了什么?对于任意锐角α,是否都有sin2α+cos2α=1 请说明理由
=(
.
=
.
=(
.
=
.
α
┗
a
b
c
sinα=
.
cosα=
.
sin2α+cos2α=
=(
.
=
.
=1
=
.
10. 如图,在△ABC中,∠A=300,
求AB。
A
B
C
D
解:过点C作CD⊥AB于点D
∠A=300,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
