3.5 圆周角 课件(共37张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 3.5 圆周角 课件(共37张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 12:05:44 | ||
图片预览




文档简介
3.5 圆周角
数学(浙教版)
九年级 上册
第3章 圆的基本性质
学习目标
1、理解圆周角的概念,会叙述并证明圆周角定理;
2、理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题;
3、理解掌握圆周角定理的推论及其证明过程和运用;
温故知新
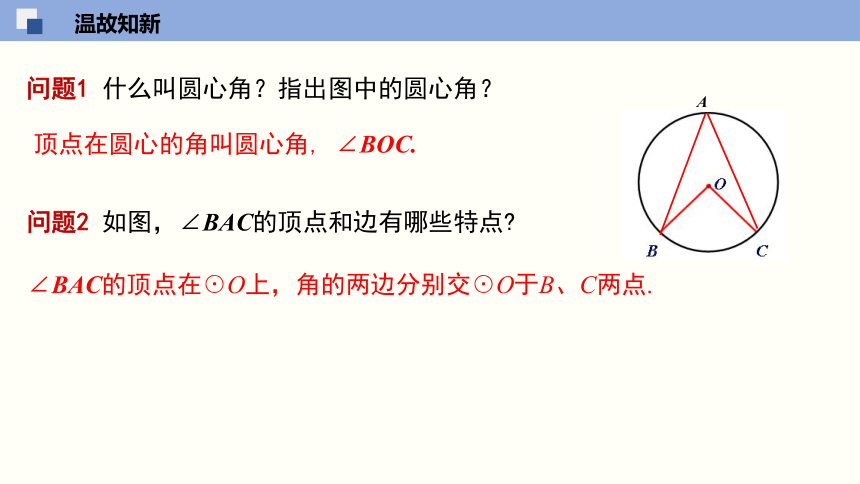
问题1 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2 如图,∠BAC的顶点和边有哪些特点?
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
讲授新课
知识点一 圆周角的定义
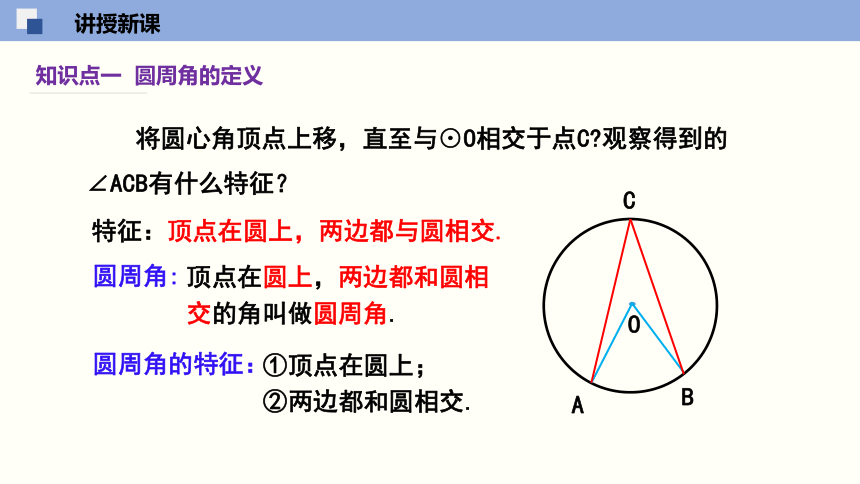
将圆心角顶点上移,直至与⊙O相交于点C?观察得到的∠ACB有什么特征?
O
A
C
B
特征:顶点在圆上,两边都与圆相交.
顶点在圆上,两边都和圆相交的角叫做圆周角.
圆周角的特征:
①顶点在圆上;
②两边都和圆相交.
圆周角:
讲授新课
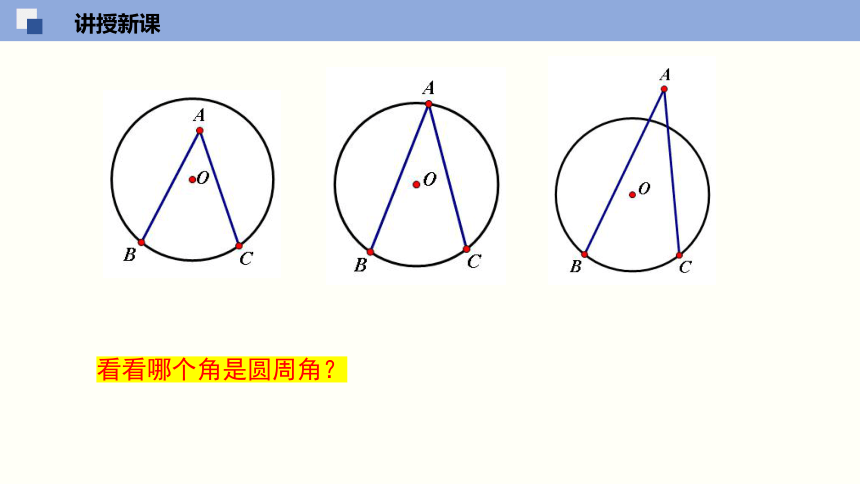
看看哪个角是圆周角?
讲授新课
【思考1】为何圆周角的定义里强调“两边都与圆相交”,而圆心角的定义里没有?
因为顶点在圆心的角,两边必然与圆相交。
O
讲授新课
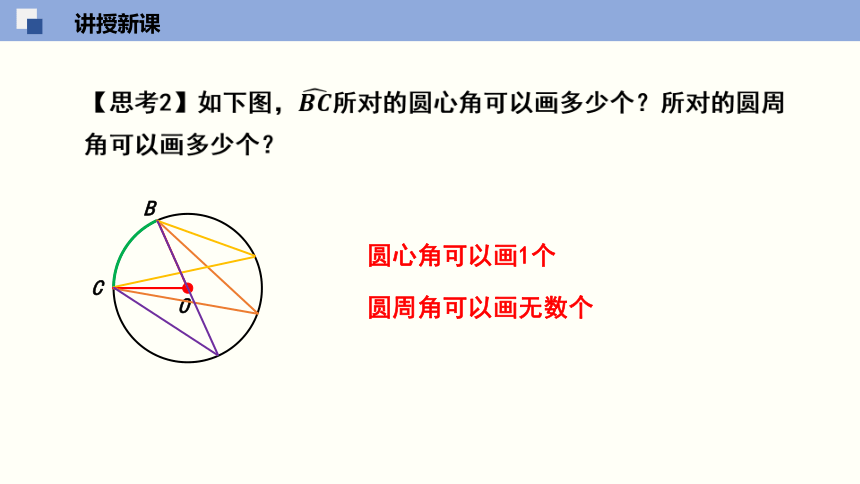
【思考2】如下图,????????所对的圆心角可以画多少个?所对的圆周角可以画多少个?
?
圆心角可以画1个
O
B
C
圆周角可以画无数个
讲授新课
圆心角
圆周角
定义
顶点在圆心
顶点在圆上;
两边都与圆相交
一条弧所对应的角的个数
只有一个
无数个
讲授新课
典例精析
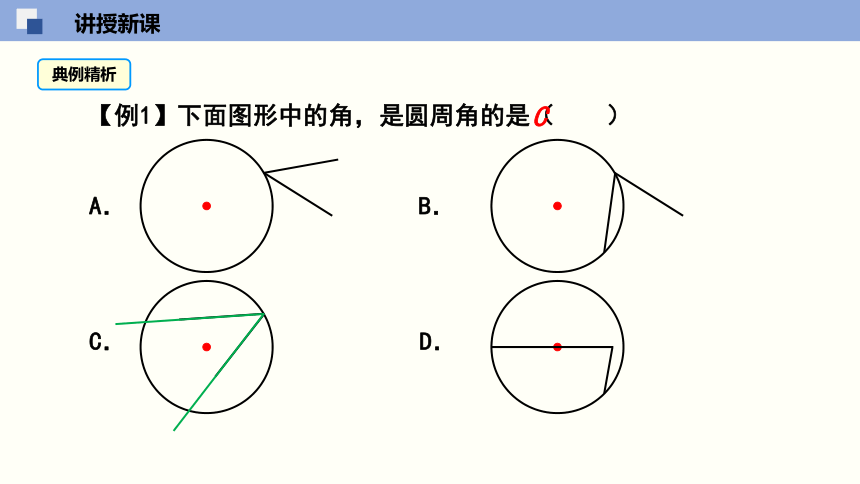
【例1】下面图形中的角,是圆周角的是( )
A. B.
C. D.
C
讲授新课
练一练
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
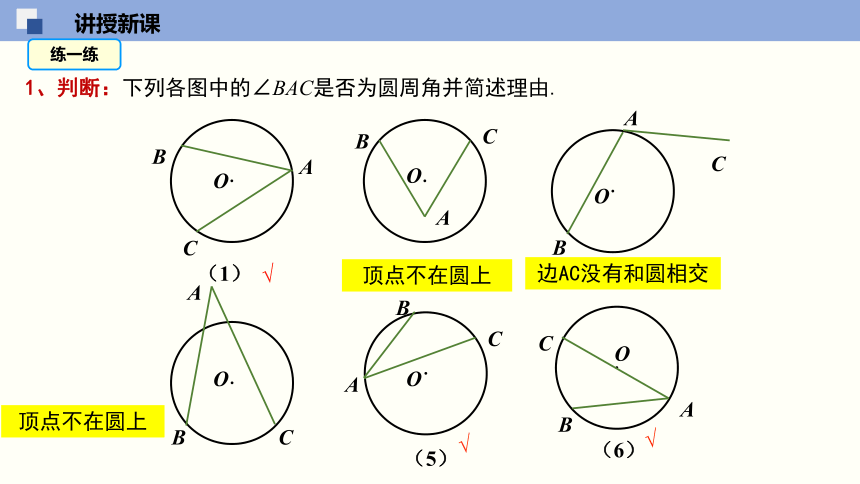
1、判断:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
讲授新课
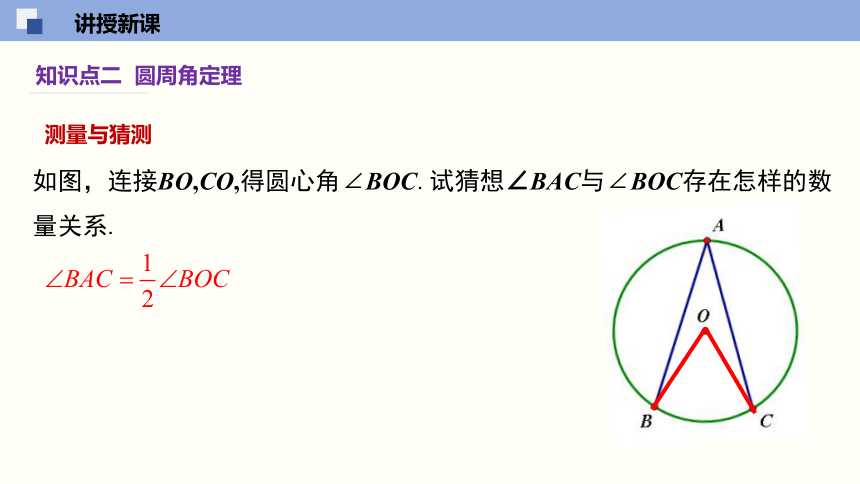
知识点二 圆周角定理
如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
测量与猜测
讲授新课
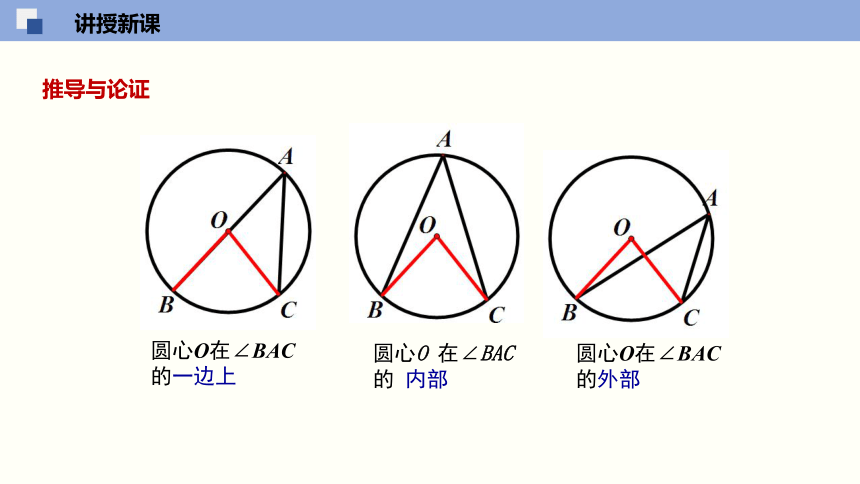
圆心O 在∠BAC的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
推导与论证
讲授新课
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
C
D
圆心O在∠BAC的内部
讲授新课
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
讲授新课
【总结】
圆周角的度数等于它所对弧上的圆心角度数的一半;
同弧所对的圆周角相等。
∵圆心角的度数=它所对的弧的度数,
∴我们也可以说,圆周角的度数=它所对的弧的度数的一半。
∵等弧所对的圆心角相等,
∴我们也可以说,等弧所对的圆周角相等。
讲授新课
圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等。
圆周角的度数等于它所对的弧的度数的一半。
公式简记:圆心角的度数=弧的度数=圆周角的度数×2。
讲授新课
典例精析
【例2】如图,在?O中,弦AB,CD相交于点P,∠CAB=40°,∠ABD=30°,则∠APD的度数为( )
A.30° B.35° C.40° D.70°
?
D
解:∵????????=????????,
∴∠D=∠CAB=40°,
∴∠APD=∠D+∠ABD=40°+30°=70°。
?
讲授新课
练一练
1、如图,A,B,C是?O上三点,若OA=AB=BC,则∠BAC的度数为( )
?A.30° B.40° C.45° D.60°
?
A
解:连接OB,OC,
∵OA=AB=BC,
∴OB=OC=BC,∴△OBC是等边三角形,
∴∠BOC=60°,
∴∠BAC=????????∠BOC=????????×60°=30°。
?
讲授新课
知识点三 圆周角定理的推论
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是圆上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
∴∠BAC=∠BDC.
解:相等.理由如下:
合作探究
∵
讲授新课
问题2 如图,若 ∠A与∠B相等吗?
解:相等.
想一想:反过来,如果∠A=∠B,那么 成立吗?
D
A
B
O
C
E
F
讲授新课
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
圆周角定理推论1
几何语言
知识要点
D
A
B
O
C
E
F
讲授新课
完成下列填空:
∠1= .
∠2= .
∠3= .
∠5= .
如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线,
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
练一练
讲授新课
思考:如图,AC是⊙O的直径,
则∠ADC = , ∠ABC= .
90°
90°
推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
O
A
C
B
D
讲授新课
典例精析
【例3】如图,AB为⊙O的直径,弦CD交AB于点P,∠ACD = 60°,∠ADC=70°. 求∠APC的度数.
. O
A
D
C
P
B
解:连接BC,如图,则∠ACB=90°,
∠DCB =∠ACB-∠ACD =
90°-60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC =∠BAD +∠ADC
=30°+70°=100°.
方法总结:在圆中,如果有直径,一般要找直径所对的圆周角,构造直角三角形解题.
讲授新课
练一练
1、如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么,∠ABC就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵OA=OB=OC,
∴△AOC、△BOC都是等腰三角形.
∴ ∠OAC=∠OCA,∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°.
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
讲授新课
2、如图,⊙O的直径AC为10cm,弦AD为6cm.
(1) 求DC的长;
解:∵AC是⊙O的直径,
∴ ∠ADC=90°.
在Rt△ADC中,
. O
A
D
C
讲授新课
(2) 若∠ADC的平分线交⊙O于B,求AB、BC的长.
B
.
O
A
D
C
解:∵ AC是⊙O的直径,∴ ∠ABC=90°.
∵DB平分∠ADC,∴∠ADB=∠CDB.
又∵∠ACB=∠ADB ,∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴ AB=BC,
∴△ABC为等腰直角三角形.
∴
方法总结:解答圆周角有关问题时,若题中出现“直径”这个条件,一般考虑构造直角三角形来求解.
当堂检测
1、如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
解析:∵BD是⊙O的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.故选C.
【点睛】在圆中,如果有直径,一般要找直径所对的圆周角,构造直角三角形解题.
C
当堂检测
2、如图,AB是⊙O的直径,弦CD交AB于点P,∠ACD=60°,∠ADC=70°.求∠APC的度数.
. O
A
D
C
P
B
解:连接BC,则∠ACB=90°,
∠DCB=∠ACB-∠ACD=90°-60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC=∠BAD+∠ADC=30°+70°=100°.
当堂检测
3、如图,AB是?O的直径,弦CD交AB于点E,连接AC、AD.若∠BAC=28°,则∠D的度数是( )
A.56° B.58° C.60° D.62°
?
D
解:如图,连接BC,
∵AB是?O的直径,∴∠ACB=90°,
∴∠ABC=90°-∠BAC=90°-28°=62°,
∵????????=????????,
∴∠B=∠D=62°。
?
当堂检测
4.如图,BC是半圆O的直径,AD⊥BC于点D,BA=AF ,BF与AD交于点E.求证:(1)∠BAD=∠ACB;(2)AE=BE.
(
(
证明:(1)∵BC是半圆O的直径,
∴∠BAC=90°.
∴∠BAD+∠CAD=90°.
∵AD⊥BC,∴∠ACB+∠CAD=90°.
∴∠BAD=∠ACB.
(2)∵BA=AF,∴∠ACB=∠ABF.
由(1)知∠BAD=∠ACB,
∴∠ABF=∠BAD.∴AE=BE.
(
(
当堂检测
5、如图,AB为?O的直径,D是弦AC延长线上一点,AC=CD,DB的延长线交?O于点E,连接CE.
(1)求证∠A=∠D;
(2)若????????的度数为108°,求∠E的度数.
?
(1)证明:连接BC,
∵AB为?O的直径,
∴∠ACB=90°,即AD⊥BC,
又∵AC=CD,∴AB=BD,
∴∠A=∠D;
?
当堂检测
(2)解:∵????????的度数为108°,∴∠EBA=54°,
又∵∠EBA=∠A+∠D,∠A=∠D,
∴∠A=????????∠EBA=27°,
又∵????????=????????,∴∠E=∠A=27°。
?
当堂检测
6、 已知 ⊙O 的弦 AB 长等于 ⊙O 的半径,求此弦 AB 所
对的圆周角的度数.
解:分下面两种情况:
如图①所示,连接OA,OB,在⊙O上任取一点C,
连接CA,CB.
∵AB=OA=OB,
∴∠AOB=60°,
∴∠ACB=1/2∠AOB=30°.
即弦AB所对的圆周角等于30°.
当堂检测
如图②所示,连接OA,OB,在劣弧上任取一点D,
连接AD,OD,BD,如图.
则∠BAD=1/2∠BOD,∠ABD=1/2∠AOD.
∴∠BAD+∠ABD=1/2(∠BOD+∠AOD)=1/2∠AOB.
∵AB的长等于⊙O的半径,
∴△AOB为等边三角形,
∴∠AOB=60°.
∴∠BAD+∠ABD=30°,
∠ADB=180°-(∠BAD+∠ABD)
=150°,
即弦AB所对的圆周角为150°.
综上所述,弦AB所对的圆周角的度数是30°或150°.
课堂小结
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等.
推论1:
推论2:
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
圆心角
圆周角
定义
顶点在圆心
顶点在圆上;
两边都与圆相交
一条弧所对应的角的个数
只有一个
无数个
谢 谢~
数学(浙教版)
九年级 上册
第3章 圆的基本性质
学习目标
1、理解圆周角的概念,会叙述并证明圆周角定理;
2、理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题;
3、理解掌握圆周角定理的推论及其证明过程和运用;
温故知新
问题1 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2 如图,∠BAC的顶点和边有哪些特点?
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
讲授新课
知识点一 圆周角的定义
将圆心角顶点上移,直至与⊙O相交于点C?观察得到的∠ACB有什么特征?
O
A
C
B
特征:顶点在圆上,两边都与圆相交.
顶点在圆上,两边都和圆相交的角叫做圆周角.
圆周角的特征:
①顶点在圆上;
②两边都和圆相交.
圆周角:
讲授新课
看看哪个角是圆周角?
讲授新课
【思考1】为何圆周角的定义里强调“两边都与圆相交”,而圆心角的定义里没有?
因为顶点在圆心的角,两边必然与圆相交。
O
讲授新课
【思考2】如下图,????????所对的圆心角可以画多少个?所对的圆周角可以画多少个?
?
圆心角可以画1个
O
B
C
圆周角可以画无数个
讲授新课
圆心角
圆周角
定义
顶点在圆心
顶点在圆上;
两边都与圆相交
一条弧所对应的角的个数
只有一个
无数个
讲授新课
典例精析
【例1】下面图形中的角,是圆周角的是( )
A. B.
C. D.
C
讲授新课
练一练
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
1、判断:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
讲授新课
知识点二 圆周角定理
如图,连接BO,CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
测量与猜测
讲授新课
圆心O 在∠BAC的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
推导与论证
讲授新课
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
C
D
圆心O在∠BAC的内部
讲授新课
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
讲授新课
【总结】
圆周角的度数等于它所对弧上的圆心角度数的一半;
同弧所对的圆周角相等。
∵圆心角的度数=它所对的弧的度数,
∴我们也可以说,圆周角的度数=它所对的弧的度数的一半。
∵等弧所对的圆心角相等,
∴我们也可以说,等弧所对的圆周角相等。
讲授新课
圆周角的度数等于它所对弧上的圆心角度数的一半,同弧或等弧所对的圆周角相等。
圆周角的度数等于它所对的弧的度数的一半。
公式简记:圆心角的度数=弧的度数=圆周角的度数×2。
讲授新课
典例精析
【例2】如图,在?O中,弦AB,CD相交于点P,∠CAB=40°,∠ABD=30°,则∠APD的度数为( )
A.30° B.35° C.40° D.70°
?
D
解:∵????????=????????,
∴∠D=∠CAB=40°,
∴∠APD=∠D+∠ABD=40°+30°=70°。
?
讲授新课
练一练
1、如图,A,B,C是?O上三点,若OA=AB=BC,则∠BAC的度数为( )
?A.30° B.40° C.45° D.60°
?
A
解:连接OB,OC,
∵OA=AB=BC,
∴OB=OC=BC,∴△OBC是等边三角形,
∴∠BOC=60°,
∴∠BAC=????????∠BOC=????????×60°=30°。
?
讲授新课
知识点三 圆周角定理的推论
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是圆上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
∴∠BAC=∠BDC.
解:相等.理由如下:
合作探究
∵
讲授新课
问题2 如图,若 ∠A与∠B相等吗?
解:相等.
想一想:反过来,如果∠A=∠B,那么 成立吗?
D
A
B
O
C
E
F
讲授新课
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
圆周角定理推论1
几何语言
知识要点
D
A
B
O
C
E
F
讲授新课
完成下列填空:
∠1= .
∠2= .
∠3= .
∠5= .
如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线,
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
练一练
讲授新课
思考:如图,AC是⊙O的直径,
则∠ADC = , ∠ABC= .
90°
90°
推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
O
A
C
B
D
讲授新课
典例精析
【例3】如图,AB为⊙O的直径,弦CD交AB于点P,∠ACD = 60°,∠ADC=70°. 求∠APC的度数.
. O
A
D
C
P
B
解:连接BC,如图,则∠ACB=90°,
∠DCB =∠ACB-∠ACD =
90°-60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC =∠BAD +∠ADC
=30°+70°=100°.
方法总结:在圆中,如果有直径,一般要找直径所对的圆周角,构造直角三角形解题.
讲授新课
练一练
1、如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么,∠ABC就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵OA=OB=OC,
∴△AOC、△BOC都是等腰三角形.
∴ ∠OAC=∠OCA,∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°.
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
讲授新课
2、如图,⊙O的直径AC为10cm,弦AD为6cm.
(1) 求DC的长;
解:∵AC是⊙O的直径,
∴ ∠ADC=90°.
在Rt△ADC中,
. O
A
D
C
讲授新课
(2) 若∠ADC的平分线交⊙O于B,求AB、BC的长.
B
.
O
A
D
C
解:∵ AC是⊙O的直径,∴ ∠ABC=90°.
∵DB平分∠ADC,∴∠ADB=∠CDB.
又∵∠ACB=∠ADB ,∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴ AB=BC,
∴△ABC为等腰直角三角形.
∴
方法总结:解答圆周角有关问题时,若题中出现“直径”这个条件,一般考虑构造直角三角形来求解.
当堂检测
1、如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
解析:∵BD是⊙O的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.故选C.
【点睛】在圆中,如果有直径,一般要找直径所对的圆周角,构造直角三角形解题.
C
当堂检测
2、如图,AB是⊙O的直径,弦CD交AB于点P,∠ACD=60°,∠ADC=70°.求∠APC的度数.
. O
A
D
C
P
B
解:连接BC,则∠ACB=90°,
∠DCB=∠ACB-∠ACD=90°-60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC=∠BAD+∠ADC=30°+70°=100°.
当堂检测
3、如图,AB是?O的直径,弦CD交AB于点E,连接AC、AD.若∠BAC=28°,则∠D的度数是( )
A.56° B.58° C.60° D.62°
?
D
解:如图,连接BC,
∵AB是?O的直径,∴∠ACB=90°,
∴∠ABC=90°-∠BAC=90°-28°=62°,
∵????????=????????,
∴∠B=∠D=62°。
?
当堂检测
4.如图,BC是半圆O的直径,AD⊥BC于点D,BA=AF ,BF与AD交于点E.求证:(1)∠BAD=∠ACB;(2)AE=BE.
(
(
证明:(1)∵BC是半圆O的直径,
∴∠BAC=90°.
∴∠BAD+∠CAD=90°.
∵AD⊥BC,∴∠ACB+∠CAD=90°.
∴∠BAD=∠ACB.
(2)∵BA=AF,∴∠ACB=∠ABF.
由(1)知∠BAD=∠ACB,
∴∠ABF=∠BAD.∴AE=BE.
(
(
当堂检测
5、如图,AB为?O的直径,D是弦AC延长线上一点,AC=CD,DB的延长线交?O于点E,连接CE.
(1)求证∠A=∠D;
(2)若????????的度数为108°,求∠E的度数.
?
(1)证明:连接BC,
∵AB为?O的直径,
∴∠ACB=90°,即AD⊥BC,
又∵AC=CD,∴AB=BD,
∴∠A=∠D;
?
当堂检测
(2)解:∵????????的度数为108°,∴∠EBA=54°,
又∵∠EBA=∠A+∠D,∠A=∠D,
∴∠A=????????∠EBA=27°,
又∵????????=????????,∴∠E=∠A=27°。
?
当堂检测
6、 已知 ⊙O 的弦 AB 长等于 ⊙O 的半径,求此弦 AB 所
对的圆周角的度数.
解:分下面两种情况:
如图①所示,连接OA,OB,在⊙O上任取一点C,
连接CA,CB.
∵AB=OA=OB,
∴∠AOB=60°,
∴∠ACB=1/2∠AOB=30°.
即弦AB所对的圆周角等于30°.
当堂检测
如图②所示,连接OA,OB,在劣弧上任取一点D,
连接AD,OD,BD,如图.
则∠BAD=1/2∠BOD,∠ABD=1/2∠AOD.
∴∠BAD+∠ABD=1/2(∠BOD+∠AOD)=1/2∠AOB.
∵AB的长等于⊙O的半径,
∴△AOB为等边三角形,
∴∠AOB=60°.
∴∠BAD+∠ABD=30°,
∠ADB=180°-(∠BAD+∠ABD)
=150°,
即弦AB所对的圆周角为150°.
综上所述,弦AB所对的圆周角的度数是30°或150°.
课堂小结
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等.
推论1:
推论2:
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
圆心角
圆周角
定义
顶点在圆心
顶点在圆上;
两边都与圆相交
一条弧所对应的角的个数
只有一个
无数个
谢 谢~
同课章节目录
