第三章圆的基本性质 圆心角与圆周角提高讲义2023-2024学年浙教版九年级数学上册
文档属性
| 名称 | 第三章圆的基本性质 圆心角与圆周角提高讲义2023-2024学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 720.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-01 17:03:32 | ||
图片预览

文档简介
圆心角与圆周角
一、知识讲解:
要点诠释
圆心角
1.定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
2.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优孤或劣弧。
3.正确理解和使用圆心角、弧、弦三者的关系
三者关系可理解为:在同圆或等圆中:①圆心角相等;②所对的弧相等;③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等。这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合。
【例1】(1)如图1,在△ABC中,,,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为_________。
(2)如图2,圆O通过五边形OABCD的四个顶点,若的度数为150°,,,则BC的度数为( )。
A.25° B.40° C.50° D.55°
(3)如图3,点A是半圆上一个三等分点(靠近点N这一侧),点B是弧AN的中点,点P是直径MN上的一个动点,若⊙O半径为3,则的最小值为_________。
【变式训练1】如图4,在⊙O中,若,则AC与2CD的大小关系是:AC_________2CD。(填“>”“<”或“=”)
【变式训练2】点A,B,C在⊙O上,,,则_________。
【例2】(1)如图5,在三角形ABC中,,⊙O截△ABC的三边所得的弦相等,则_________。
(2)如图6,在同圆中,弧AB等于弧CD的2倍,试判断AB与2CD的大小关系是
A. B. C. D.不能确定
【变式训练3】如图7,已知AB、CD是⊙O的直径,,,则∠COE的度数为________度。
【变式训练4】如图8,已知半⊙O的直径AB为3,弦AC与弦BD交于点E,OD⊥AC,垂足为点F,,则弦AC的长为________。
【变式训练5】如图9,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E。则下列结论:
①,②,③,④四边形AODC是菱形。
正确的个数是________。
【变式训练6】如图10,A、B、C、D是⊙O上的四个点,若,且弦,,则⊙O的半径为________。
【变式训练7】如图11,⊙O的半径为1cm,弦AB、CD的长度分别为,1cm,则弦AC、BD所夹的锐角________度。
【变式训练8】如图12,在平面直角坐标系xOy中,扇形OAB的圆心角,点A在x轴正半轴上且,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在扇形OAB内(不含边界),则点E的横坐标x取值范围为________。
要点诠释
圆周角
1.圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫作圆周角。
注意:圆周角必须满足两个条件:①顶点在圆上;②角的两条边都与圆相交,二者缺一不可。
2.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
3.在解圆的有关问题时,常常需要添加辅助线,构成直径所对的圆周角,这种基本技能技巧一定要掌握。
4.注意:①圆周角和圆心角的转化可通过作圆的半径构造等腰三角形,利用等腰三角形的顶点和底角的关系进行转化;②圆周角和圆周角的转化可利用其“桥梁”一圆心角转化;③定理成立的条件是“同一条弧所对的”两种角,在运用定理时不要忽略了这个条件,把不同弧所对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角。
【例1】如图13,AB是⊙O的直径,点C,D都在⊙O上,,则∠BDC的大小是________。
【变式训练1】如图14,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则_________度。
【变式训练2】如图15,点A,B,C在⊙O上,AD是∠BAC的角平分线,若,则∠CAD的度数为_________。
【变式训练3】如图16,AB为⊙O的直径,点C、D在⊙O上,若,则∠D的度数是_________。
【变式训练4】如图17,A,B,P是半径为2的⊙O上的三点,,则弦AB的长为( )。
A.2 B.4 C. D.
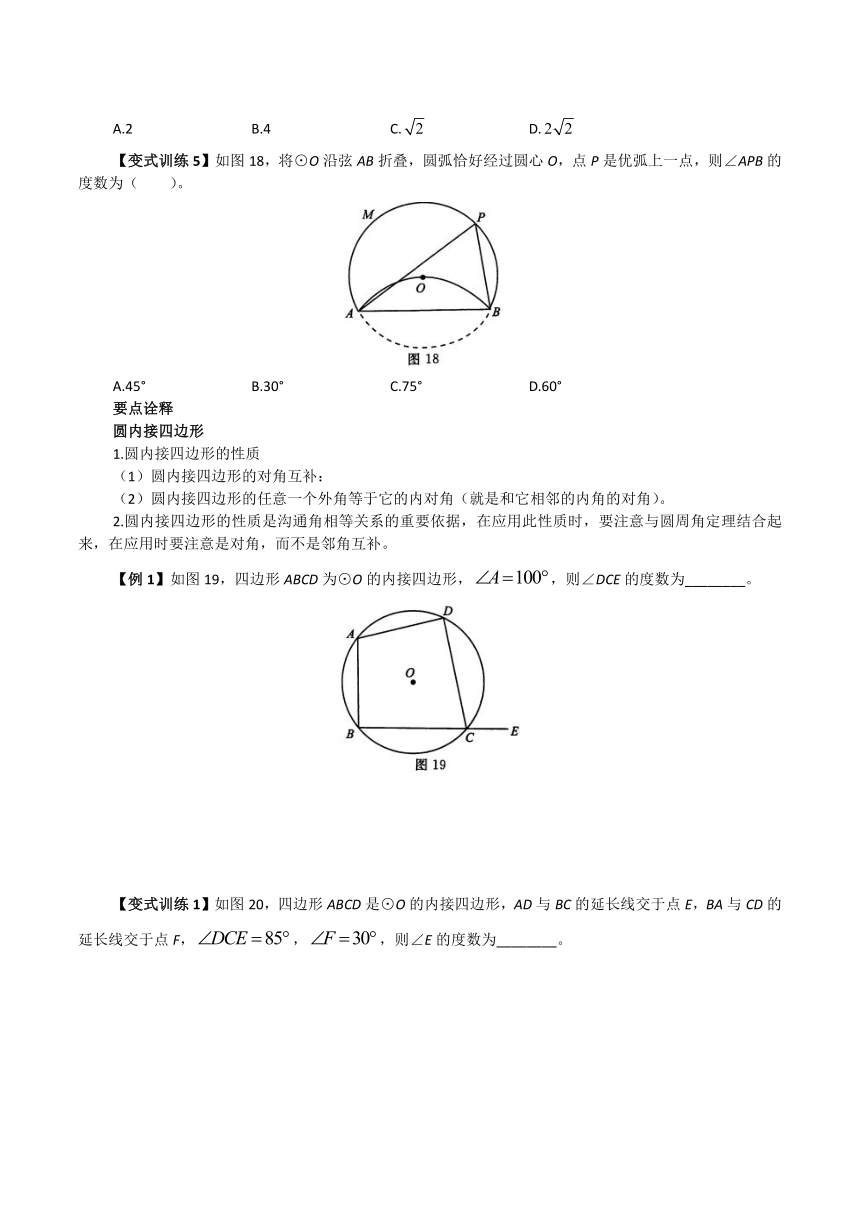
【变式训练5】如图18,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧上一点,则∠APB的度数为( )。
A.45° B.30° C.75° D.60°
要点诠释
圆内接四边形
1.圆内接四边形的性质
(1)圆内接四边形的对角互补:
(2)圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角)。
2.圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来,在应用时要注意是对角,而不是邻角互补。
【例1】如图19,四边形ABCD为⊙O的内接四边形,,则∠DCE的度数为________。
【变式训练1】如图20,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,,,则∠E的度数为________。
【变式训练2】如图21,点A、B、C、D、E在⊙O上,且为50°,则________。
【变式训练3】如图22,点A,B,C,D在⊙O上,,,,则________。
【变式训练4】如图23,A、B、C是⊙O上的三点,且四边形OABC是菱形,若点D是圆上异于A、B、C的另一点,则∠ADC的度数是________。
【变式训练5】如图24,在圆O的内接四边形ABCD中,,,,点C为的中点,则AC的长是________。
【变式训练6】如图25,AE是半圆O的直径,弦,弦,连结OB,OD,则图中两个阴影部分的面积和为________。
要点诠释
正多边形
把一个圆分成n(是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫作这个正多边形的外接圆。
【例1】如图26,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若,则这个正多边形的边数为________。
【变式训练1】如图27,图①、图②、图③、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
(1)求图①中∠APN的度数是________;图②中,∠APN的度数是________;图③中∠APN的度数是________。
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)________。
【变式训练2】(1)已知:如图28,图①△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点。求证:;
(2)已知:如图②四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点。求证:。
【变式训练3】(1)如图29,图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点且,连接OM、ON,求∠MON的度数;
(2)图②、③、…④中,M、N分别是⊙O的内接正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且,连接OM、ON,则图②中∠MON的度数是________;图③中∠MON的度数是________;…由此可猜测在n边形图中∠MON的度数是________;
(3)若3,各自有一个正多边形,则从中任取2个图形,恰好都是中心对称图形的概率是________。
【变式训练4】如图30,在正六边形ABCDEF中,是AB边上一点,交EF于,交CD于。
(1)直接写出的值为_________。
(2)若,①求证:;②求的值。
二、课后作业
1.有下列说法:①直径是圆中最长的弦;②等弧所对的弦相等;③圆中90°的角所对的弦是直径;④相等的圆心角对的弧相等。其中正确的有( )。
A.1个 B.2个 C.3个 D.4个
2.如图1,圆O通过五边形OABCD的四个顶点,若,,,则的度数为( )。
A.25° B.40° C.50° D.60°
3.如图2,A、B、C、D四个点均在⊙O上,,弦DC的长等于半径,则∠B的度数为( )。
A.40° B.45° C.50° D.55°
4.如图3,A、B、C、D四点在⊙O上的位置,其中,且,。若在上取一点P,在上取一点Q,使得,则下列叙述正确的是( )。
A.Q点在上,且 B.Q点在上,且
C.Q点在上,且 D.Q点在上,且
5.如图4,在⊙O中,弦AB所对的圆周角,,,则∠A度数为( )。
A.30° B.36° C.45° D.60°
6.如图5,在⊙O中,,,则∠BDC的度数是( )。
A.10° B.20° C.30° D.40°
7.如图6,AB是⊙O的直径,CD为⊙O的弦,且CD⊥AB于点E,点F为圆上一点,若,,,则BC的长为( )。
A. B. C.4 D.5
8.如图7,AB是⊙O的直径,点D,C在⊙O上,,,,则⊙O的半径为( )。
A. B. C. D.
9.如图8,四边形ABCD是⊙O的内接四边形,,若,则∠ABD的度数是________。
10.如图9,点A、B、C、D、E在⊙O上,且的度数为50°,则________。
11.如图10,AC是⊙O的弦,,点B是⊙O上的一个动点,且,若点M、N分别是AC、BC的中点,则MN的最大值是________。
12.如图11,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC、PD,DG⊥PC,垂足为G,∠PDG等于________度。
13.如图12,在△ABC中,,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且,则BE长为________。
14.如图13,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F。
(1)若时,求证:;
(2)若时,求∠A的度数;
(3)若,,且。请你用含有、的代数式表示∠A的大小。
5.如图14,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若。
(1)求证:;
(2)若,,求CD的长。
16.如图15,正方形ABCD的四个顶点都在⊙O上,E是⊙O上的一点。
(1)如图①,若点E在AB上,F是DE上的一点,。求证:△ADF≌△ABE;
(2)在(1)的条件下,小明还发现线段DE、BE、AE之间满足等量关系:。请你说明理由;
(3)如图②,若点E在上。写出线段DE、BE、AE之间的等量关系。(不必证明)
17.如图16,在⊙O中,点P为的中点,弦AD、PC互相垂直,垂足为M,BC分别与AD、PD相交于点E、N,连接BD、MN。
(1)求证:N为BE的中点;
(2)若⊙O的半径为8,的度数为90°,求线段MN的长。
一、知识讲解:
要点诠释
圆心角
1.定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
2.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优孤或劣弧。
3.正确理解和使用圆心角、弧、弦三者的关系
三者关系可理解为:在同圆或等圆中:①圆心角相等;②所对的弧相等;③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等。这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合。
【例1】(1)如图1,在△ABC中,,,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为_________。
(2)如图2,圆O通过五边形OABCD的四个顶点,若的度数为150°,,,则BC的度数为( )。
A.25° B.40° C.50° D.55°
(3)如图3,点A是半圆上一个三等分点(靠近点N这一侧),点B是弧AN的中点,点P是直径MN上的一个动点,若⊙O半径为3,则的最小值为_________。
【变式训练1】如图4,在⊙O中,若,则AC与2CD的大小关系是:AC_________2CD。(填“>”“<”或“=”)
【变式训练2】点A,B,C在⊙O上,,,则_________。
【例2】(1)如图5,在三角形ABC中,,⊙O截△ABC的三边所得的弦相等,则_________。
(2)如图6,在同圆中,弧AB等于弧CD的2倍,试判断AB与2CD的大小关系是
A. B. C. D.不能确定
【变式训练3】如图7,已知AB、CD是⊙O的直径,,,则∠COE的度数为________度。
【变式训练4】如图8,已知半⊙O的直径AB为3,弦AC与弦BD交于点E,OD⊥AC,垂足为点F,,则弦AC的长为________。
【变式训练5】如图9,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E。则下列结论:
①,②,③,④四边形AODC是菱形。
正确的个数是________。
【变式训练6】如图10,A、B、C、D是⊙O上的四个点,若,且弦,,则⊙O的半径为________。
【变式训练7】如图11,⊙O的半径为1cm,弦AB、CD的长度分别为,1cm,则弦AC、BD所夹的锐角________度。
【变式训练8】如图12,在平面直角坐标系xOy中,扇形OAB的圆心角,点A在x轴正半轴上且,点C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在扇形OAB内(不含边界),则点E的横坐标x取值范围为________。
要点诠释
圆周角
1.圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫作圆周角。
注意:圆周角必须满足两个条件:①顶点在圆上;②角的两条边都与圆相交,二者缺一不可。
2.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。
3.在解圆的有关问题时,常常需要添加辅助线,构成直径所对的圆周角,这种基本技能技巧一定要掌握。
4.注意:①圆周角和圆心角的转化可通过作圆的半径构造等腰三角形,利用等腰三角形的顶点和底角的关系进行转化;②圆周角和圆周角的转化可利用其“桥梁”一圆心角转化;③定理成立的条件是“同一条弧所对的”两种角,在运用定理时不要忽略了这个条件,把不同弧所对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角。
【例1】如图13,AB是⊙O的直径,点C,D都在⊙O上,,则∠BDC的大小是________。
【变式训练1】如图14,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则_________度。
【变式训练2】如图15,点A,B,C在⊙O上,AD是∠BAC的角平分线,若,则∠CAD的度数为_________。
【变式训练3】如图16,AB为⊙O的直径,点C、D在⊙O上,若,则∠D的度数是_________。
【变式训练4】如图17,A,B,P是半径为2的⊙O上的三点,,则弦AB的长为( )。
A.2 B.4 C. D.
【变式训练5】如图18,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧上一点,则∠APB的度数为( )。
A.45° B.30° C.75° D.60°
要点诠释
圆内接四边形
1.圆内接四边形的性质
(1)圆内接四边形的对角互补:
(2)圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角)。
2.圆内接四边形的性质是沟通角相等关系的重要依据,在应用此性质时,要注意与圆周角定理结合起来,在应用时要注意是对角,而不是邻角互补。
【例1】如图19,四边形ABCD为⊙O的内接四边形,,则∠DCE的度数为________。
【变式训练1】如图20,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,,,则∠E的度数为________。
【变式训练2】如图21,点A、B、C、D、E在⊙O上,且为50°,则________。
【变式训练3】如图22,点A,B,C,D在⊙O上,,,,则________。
【变式训练4】如图23,A、B、C是⊙O上的三点,且四边形OABC是菱形,若点D是圆上异于A、B、C的另一点,则∠ADC的度数是________。
【变式训练5】如图24,在圆O的内接四边形ABCD中,,,,点C为的中点,则AC的长是________。
【变式训练6】如图25,AE是半圆O的直径,弦,弦,连结OB,OD,则图中两个阴影部分的面积和为________。
要点诠释
正多边形
把一个圆分成n(是大于2的自然数)等份,依次连接各分点所得的多边形是这个圆的内接正多边形,这个圆叫作这个正多边形的外接圆。
【例1】如图26,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若,则这个正多边形的边数为________。
【变式训练1】如图27,图①、图②、图③、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
(1)求图①中∠APN的度数是________;图②中,∠APN的度数是________;图③中∠APN的度数是________。
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)________。
【变式训练2】(1)已知:如图28,图①△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点。求证:;
(2)已知:如图②四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点。求证:。
【变式训练3】(1)如图29,图①,M、N分别是⊙O的内接正△ABC的边AB、BC上的点且,连接OM、ON,求∠MON的度数;
(2)图②、③、…④中,M、N分别是⊙O的内接正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且,连接OM、ON,则图②中∠MON的度数是________;图③中∠MON的度数是________;…由此可猜测在n边形图中∠MON的度数是________;
(3)若3,各自有一个正多边形,则从中任取2个图形,恰好都是中心对称图形的概率是________。
【变式训练4】如图30,在正六边形ABCDEF中,是AB边上一点,交EF于,交CD于。
(1)直接写出的值为_________。
(2)若,①求证:;②求的值。
二、课后作业
1.有下列说法:①直径是圆中最长的弦;②等弧所对的弦相等;③圆中90°的角所对的弦是直径;④相等的圆心角对的弧相等。其中正确的有( )。
A.1个 B.2个 C.3个 D.4个
2.如图1,圆O通过五边形OABCD的四个顶点,若,,,则的度数为( )。
A.25° B.40° C.50° D.60°
3.如图2,A、B、C、D四个点均在⊙O上,,弦DC的长等于半径,则∠B的度数为( )。
A.40° B.45° C.50° D.55°
4.如图3,A、B、C、D四点在⊙O上的位置,其中,且,。若在上取一点P,在上取一点Q,使得,则下列叙述正确的是( )。
A.Q点在上,且 B.Q点在上,且
C.Q点在上,且 D.Q点在上,且
5.如图4,在⊙O中,弦AB所对的圆周角,,,则∠A度数为( )。
A.30° B.36° C.45° D.60°
6.如图5,在⊙O中,,,则∠BDC的度数是( )。
A.10° B.20° C.30° D.40°
7.如图6,AB是⊙O的直径,CD为⊙O的弦,且CD⊥AB于点E,点F为圆上一点,若,,,则BC的长为( )。
A. B. C.4 D.5
8.如图7,AB是⊙O的直径,点D,C在⊙O上,,,,则⊙O的半径为( )。
A. B. C. D.
9.如图8,四边形ABCD是⊙O的内接四边形,,若,则∠ABD的度数是________。
10.如图9,点A、B、C、D、E在⊙O上,且的度数为50°,则________。
11.如图10,AC是⊙O的弦,,点B是⊙O上的一个动点,且,若点M、N分别是AC、BC的中点,则MN的最大值是________。
12.如图11,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC、PD,DG⊥PC,垂足为G,∠PDG等于________度。
13.如图12,在△ABC中,,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且,则BE长为________。
14.如图13,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F。
(1)若时,求证:;
(2)若时,求∠A的度数;
(3)若,,且。请你用含有、的代数式表示∠A的大小。
5.如图14,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若。
(1)求证:;
(2)若,,求CD的长。
16.如图15,正方形ABCD的四个顶点都在⊙O上,E是⊙O上的一点。
(1)如图①,若点E在AB上,F是DE上的一点,。求证:△ADF≌△ABE;
(2)在(1)的条件下,小明还发现线段DE、BE、AE之间满足等量关系:。请你说明理由;
(3)如图②,若点E在上。写出线段DE、BE、AE之间的等量关系。(不必证明)
17.如图16,在⊙O中,点P为的中点,弦AD、PC互相垂直,垂足为M,BC分别与AD、PD相交于点E、N,连接BD、MN。
(1)求证:N为BE的中点;
(2)若⊙O的半径为8,的度数为90°,求线段MN的长。
同课章节目录
