3.8 弧长及扇形面积(第2课时)课件(共30张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 3.8 弧长及扇形面积(第2课时)课件(共30张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 21:33:39 | ||
图片预览








文档简介
3.8 弧长及扇形面积
第2课时 扇形的面积及应用
数学(浙教版)
九年级 上册
第3章 圆的基本性质
学习目标
1.理解扇形面积公式的探求过程;
2.会利用扇形面积的计算公式进行计算;
温故知新
【注意】用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
弧长公式
半径为R的圆中,圆心角为n°的弧长
导入新课
如图,由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形. (记作:扇形OAB) ?
扇形的面积除了与圆的半径有关外还与组成扇形的圆心角的大小有关.圆心角越大,扇形面积也就越大.怎样计算圆半径为R,圆心角为n°的扇形面积呢?
讲授新课
知识点一 扇形面积及应用
【探究】仿照弧长公式的推导过程,探究当圆的半径R确定时,扇形的面积S扇形与扇形的圆心角度数n之间的数量关系~
圆心角为360°的扇形的面积就是圆的面积πR2
圆心角为1°的扇形的面积为????????????????πR2
?
圆心角为n°的扇形的面积为????????????????πR2
?
讲授新课
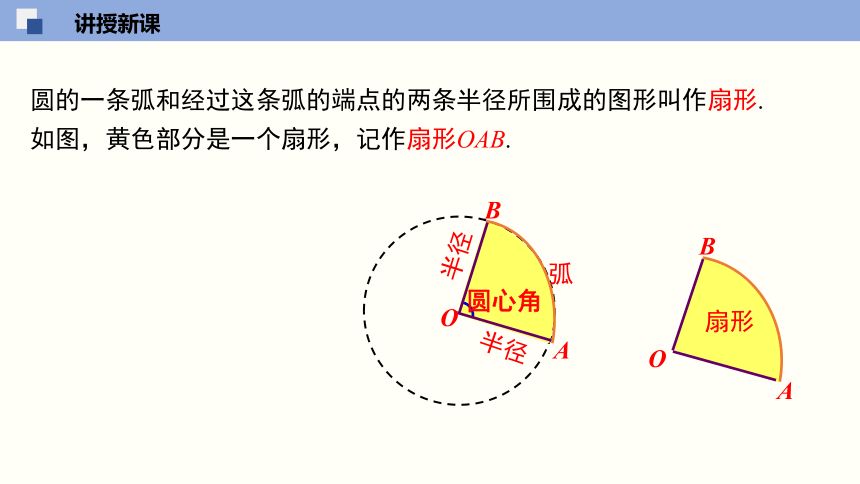
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
讲授新课
猜一猜:
有风不动无风动,
不动无风动有风.
(打一夏季常用生活用品)
讲授新课
S=πR2
(2)圆心角为1°的扇形的面积是多少?
(3)圆心角为n°的扇形的面积是圆心角为1°
的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少?
思考
(1)半径为R的圆,面积是多少?
合作探究
讲授新课
扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
要点归纳
讲授新课
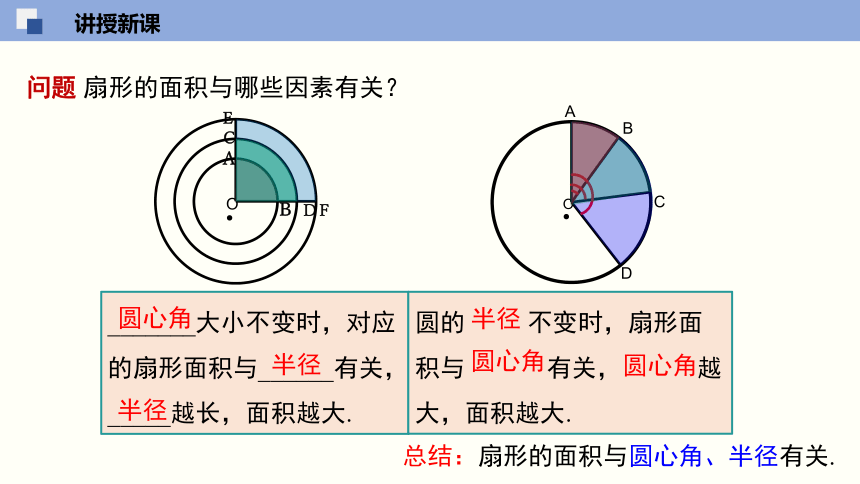
_______大小不变时,对应的扇形面积与______有关,
_____越长,面积越大.
圆心角
半径
半径
圆的 不变时,扇形面积与 有关, 越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
问题 扇形的面积与哪些因素有关?
讲授新课
在半径R的圆中,扇形的面积S扇形与弧长l之间有如下关系:
S扇形=????????lR。
?
∵S扇形=????????????????πR2=????????·????????????????????·R,
∴S扇形=????????lR
?
上述公式揭示了S扇形与n、R之间的数量关系,试探索S扇形与l、R之间的数量关系。
讲授新课
典例精析
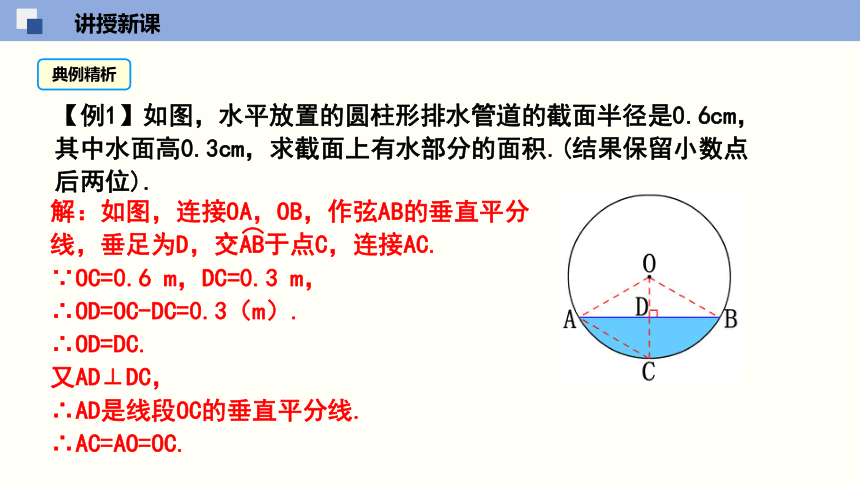
【例1】如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(结果保留小数点后两位).
解:如图,连接OA,OB,作弦AB的垂直平分线,垂足为D,交AB于点C,连接AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
(
讲授新课
从而∠AOD=60°,∠AOB=120°.
有水部分的面积
讲授新课
练一练
1.已知扇形的圆心角为120?,半径为2,则这个扇形的面积为____.
2.已知扇形的圆心角为30?,面积为3πcm?,则这个扇形的半径R=_____.
3.已知扇形的圆心角为150?,弧长为20πcm,则扇形的面积为________.
6cm
240πcm2
讲授新课
4.半径为6cm,圆心角为40°的扇形面积是______cm2.
5.扇形的弧长为2πcm,半径为3cm,则扇形面积为_____cm2.
4π
3π
讲授新课
知识点二 弓形的面积计算
弓形的定义?
如图,一条弦和这条弦所对的弧组成的图形叫做弓形。
O
讲授新课
以下三种类型的弓形的面积(阴影部分的面积)如何计算?
O
A
B
O
A
B
S弓形=S扇形AOB-S△AOB
S弓形=S扇形AOB+S△AOB
S弓形=????????S圆
?
和差法
讲授新课
典例精析
【例2】如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为________.
????????π-????
?
【分析】由题意可知:∠AOB=60°,
∵OA=OB,∴△AOB为等边三角形,
∴AB=AO=BO=2,
∴S△AOB=????????×22=????,S扇形AOB=????????????×????????????????????=????????π,
∴阴影部分的面积为:S扇形AOB-S△AOB=????????π-????.
?
A
B
O
讲授新课
练一练
1、如图,将半径为2cm的圆形纸片翻折,使得????????,????????恰好都经过圆心O,折痕为AB,BC,则阴影部分的面积为________.
?
43π
?
【分析】如图,作OD⊥AB于点D,连接AO,BO,CO,
∵OD=12AO,∴∠OAD=30°,∠AOD=60°,
∴∠AOB=2∠AOD=120°,
同理:∠BOC=120°,∴∠AOC=120°,
∴阴影部分的面积=S扇形AOC=120????×22360=43π(cm2).
?
割补法
当堂检测
1.如图,☉A、☉B、 ☉C、 ☉D两两不相交,且半径都是2cm,则图中阴影部分的面积是 .
A
B
C
D
当堂检测
2、如图,已知圆O的半径1.5cm,圆心角∠AOB=58o,求扇形OAB的面积(结果精确到0.1cm2)
58o
O
A
B
解 ∵r=1.5cm, n=58,
当堂检测
3.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为多少度?
解:设扇形半径为R,圆心角为n0,由扇形
公式
答:该扇形的圆心角为150度.
(cm)
可得:
当堂检测
4、 如图是一条圆弧形弯道,已知OA=20m,OC=12m, 弧CD的长度为9πm,求圆弧形弯道的面积.
解:设∠AOB=n°,
∵OC=12m,弧CD的长度为9πm,
解得n=135,即圆心∠COD=135°,
当堂检测
答:圆弧形弯道的面积为 .
当堂检测
5、如图,在?ABCD中,AB=4cm,BC=22cm,∠ABC=135°,将?ABCD绕点A逆时针旋转一定的角度,使点B的对应点B'恰好落在CD边上,则边BC扫过的面积(图中阴影部分)是________cm2.
?
【分析】如图,连接AC,AC′,过C点作CE⊥AB交AB的延长线于E,过B′点作B′F⊥AB交AB于F,
∵∠ABC=135°,∴∠CBE=45°,
∵BC=22cm,CE⊥AB,∴CE=BE=2cm,
∵AB=4cm,∴AC=????????2+????????2=210(cm),
?
当堂检测
∵CE⊥AB,B′F⊥AB,∴CE∥B′F,
∴四边形B′FEC是平行四边形,∴B′F=CE=2cm,
由旋转可知:AB′=AB=4cm,
∴AB′=12B′F,∴∠BAB′=30°,
?
由旋转可知:∠B′AC′=∠BAC,
∴∠CAC′=∠B′AC+∠B′AC′=∠B′AC+∠BAC=∠BAB′=30°,
由旋转可知:△AB′C′的面积等于△ABC的面积,
∴阴影部分的面积=S扇形ACC′-S扇形ABB′
=30????×2102360?30????×42360=2π(cm2).
?
割补法+和差法
当堂检测
6.如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.
(1)求证:∠ACO=∠BCP;
(2)若∠ABC=2∠BCP,求∠P的度数;
(1)证明:∵AB是半圆O的直径,∴∠ACB=90°,
∵CP是半圆O的切线,
∴∠OCP=90°,
∴∠ACB=∠OCP,
∴∠ACO=∠BCP;
当堂检测
(2)解:由(1)知∠ACO=∠BCP,
∵∠ABC=2∠BCP,
∴∠ABC=2∠ACO,
∵OA=OC,
∴∠ACO=∠A,
∴∠ABC=2∠A,
∵∠ABC+∠A=90°,
∴∠A=30°,∠ABC=60°,
∴∠ACO=∠BCP=30°,
∴∠P=∠ABC﹣∠BCP=60°﹣30°=30°.
课堂小结
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
谢 谢~
第2课时 扇形的面积及应用
数学(浙教版)
九年级 上册
第3章 圆的基本性质
学习目标
1.理解扇形面积公式的探求过程;
2.会利用扇形面积的计算公式进行计算;
温故知新
【注意】用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
弧长公式
半径为R的圆中,圆心角为n°的弧长
导入新课
如图,由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形. (记作:扇形OAB) ?
扇形的面积除了与圆的半径有关外还与组成扇形的圆心角的大小有关.圆心角越大,扇形面积也就越大.怎样计算圆半径为R,圆心角为n°的扇形面积呢?
讲授新课
知识点一 扇形面积及应用
【探究】仿照弧长公式的推导过程,探究当圆的半径R确定时,扇形的面积S扇形与扇形的圆心角度数n之间的数量关系~
圆心角为360°的扇形的面积就是圆的面积πR2
圆心角为1°的扇形的面积为????????????????πR2
?
圆心角为n°的扇形的面积为????????????????πR2
?
讲授新课
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
如图,黄色部分是一个扇形,记作扇形OAB.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
讲授新课
猜一猜:
有风不动无风动,
不动无风动有风.
(打一夏季常用生活用品)
讲授新课
S=πR2
(2)圆心角为1°的扇形的面积是多少?
(3)圆心角为n°的扇形的面积是圆心角为1°
的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少?
思考
(1)半径为R的圆,面积是多少?
合作探究
讲授新课
扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为
①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆).
注意
要点归纳
讲授新课
_______大小不变时,对应的扇形面积与______有关,
_____越长,面积越大.
圆心角
半径
半径
圆的 不变时,扇形面积与 有关, 越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O ●
A
B
D
C
E
F
O ●
A
B
C
D
问题 扇形的面积与哪些因素有关?
讲授新课
在半径R的圆中,扇形的面积S扇形与弧长l之间有如下关系:
S扇形=????????lR。
?
∵S扇形=????????????????πR2=????????·????????????????????·R,
∴S扇形=????????lR
?
上述公式揭示了S扇形与n、R之间的数量关系,试探索S扇形与l、R之间的数量关系。
讲授新课
典例精析
【例1】如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(结果保留小数点后两位).
解:如图,连接OA,OB,作弦AB的垂直平分线,垂足为D,交AB于点C,连接AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
(
讲授新课
从而∠AOD=60°,∠AOB=120°.
有水部分的面积
讲授新课
练一练
1.已知扇形的圆心角为120?,半径为2,则这个扇形的面积为____.
2.已知扇形的圆心角为30?,面积为3πcm?,则这个扇形的半径R=_____.
3.已知扇形的圆心角为150?,弧长为20πcm,则扇形的面积为________.
6cm
240πcm2
讲授新课
4.半径为6cm,圆心角为40°的扇形面积是______cm2.
5.扇形的弧长为2πcm,半径为3cm,则扇形面积为_____cm2.
4π
3π
讲授新课
知识点二 弓形的面积计算
弓形的定义?
如图,一条弦和这条弦所对的弧组成的图形叫做弓形。
O
讲授新课
以下三种类型的弓形的面积(阴影部分的面积)如何计算?
O
A
B
O
A
B
S弓形=S扇形AOB-S△AOB
S弓形=S扇形AOB+S△AOB
S弓形=????????S圆
?
和差法
讲授新课
典例精析
【例2】如图,有一个半径为2的圆形时钟,其中每个相邻刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为________.
????????π-????
?
【分析】由题意可知:∠AOB=60°,
∵OA=OB,∴△AOB为等边三角形,
∴AB=AO=BO=2,
∴S△AOB=????????×22=????,S扇形AOB=????????????×????????????????????=????????π,
∴阴影部分的面积为:S扇形AOB-S△AOB=????????π-????.
?
A
B
O
讲授新课
练一练
1、如图,将半径为2cm的圆形纸片翻折,使得????????,????????恰好都经过圆心O,折痕为AB,BC,则阴影部分的面积为________.
?
43π
?
【分析】如图,作OD⊥AB于点D,连接AO,BO,CO,
∵OD=12AO,∴∠OAD=30°,∠AOD=60°,
∴∠AOB=2∠AOD=120°,
同理:∠BOC=120°,∴∠AOC=120°,
∴阴影部分的面积=S扇形AOC=120????×22360=43π(cm2).
?
割补法
当堂检测
1.如图,☉A、☉B、 ☉C、 ☉D两两不相交,且半径都是2cm,则图中阴影部分的面积是 .
A
B
C
D
当堂检测
2、如图,已知圆O的半径1.5cm,圆心角∠AOB=58o,求扇形OAB的面积(结果精确到0.1cm2)
58o
O
A
B
解 ∵r=1.5cm, n=58,
当堂检测
3.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为多少度?
解:设扇形半径为R,圆心角为n0,由扇形
公式
答:该扇形的圆心角为150度.
(cm)
可得:
当堂检测
4、 如图是一条圆弧形弯道,已知OA=20m,OC=12m, 弧CD的长度为9πm,求圆弧形弯道的面积.
解:设∠AOB=n°,
∵OC=12m,弧CD的长度为9πm,
解得n=135,即圆心∠COD=135°,
当堂检测
答:圆弧形弯道的面积为 .
当堂检测
5、如图,在?ABCD中,AB=4cm,BC=22cm,∠ABC=135°,将?ABCD绕点A逆时针旋转一定的角度,使点B的对应点B'恰好落在CD边上,则边BC扫过的面积(图中阴影部分)是________cm2.
?
【分析】如图,连接AC,AC′,过C点作CE⊥AB交AB的延长线于E,过B′点作B′F⊥AB交AB于F,
∵∠ABC=135°,∴∠CBE=45°,
∵BC=22cm,CE⊥AB,∴CE=BE=2cm,
∵AB=4cm,∴AC=????????2+????????2=210(cm),
?
当堂检测
∵CE⊥AB,B′F⊥AB,∴CE∥B′F,
∴四边形B′FEC是平行四边形,∴B′F=CE=2cm,
由旋转可知:AB′=AB=4cm,
∴AB′=12B′F,∴∠BAB′=30°,
?
由旋转可知:∠B′AC′=∠BAC,
∴∠CAC′=∠B′AC+∠B′AC′=∠B′AC+∠BAC=∠BAB′=30°,
由旋转可知:△AB′C′的面积等于△ABC的面积,
∴阴影部分的面积=S扇形ACC′-S扇形ABB′
=30????×2102360?30????×42360=2π(cm2).
?
割补法+和差法
当堂检测
6.如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.
(1)求证:∠ACO=∠BCP;
(2)若∠ABC=2∠BCP,求∠P的度数;
(1)证明:∵AB是半圆O的直径,∴∠ACB=90°,
∵CP是半圆O的切线,
∴∠OCP=90°,
∴∠ACB=∠OCP,
∴∠ACO=∠BCP;
当堂检测
(2)解:由(1)知∠ACO=∠BCP,
∵∠ABC=2∠BCP,
∴∠ABC=2∠ACO,
∵OA=OC,
∴∠ACO=∠A,
∴∠ABC=2∠A,
∵∠ABC+∠A=90°,
∴∠A=30°,∠ABC=60°,
∴∠ACO=∠BCP=30°,
∴∠P=∠ABC﹣∠BCP=60°﹣30°=30°.
课堂小结
扇形
定义
公式
阴影部分面积
求法:整体思想
弓形
公式
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
谢 谢~
同课章节目录
