4.2 由平行线截得的比例线段 课件(共21张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 4.2 由平行线截得的比例线段 课件(共21张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 00:00:00 | ||
图片预览







文档简介
4.2 由平行线截得的比例线段
数学(浙教版)
九年级 上册
第4章 相似三角形
学习目标
1.理解平行线分线段成比例的基本事实及其推论;
2.掌握平行线分线段成比例的基本事实及其推论进行证明和计算;
温故知新
四条线段 a、b、c、d 中,如果 a:b=c:d,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.
比例的基本性质:
比例线段的概念:
等比的性质:
合比的性质:
如果ab=cd=…=mn (b+d+…+n≠0),那么a+c+…+m?b+d+…+n=ab.
?
如果????????=????????,,那么????+????????=????+????????, ?????????????=??????????????.
?
导入新课
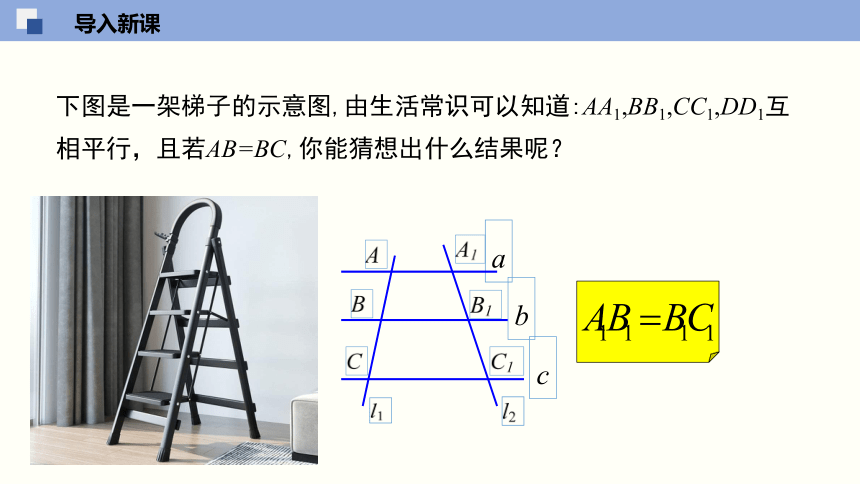
下图是一架梯子的示意图,由生活常识可以知道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
讲授新课
知识点一 平行线分线段成比例概念
算一算下列线段的比值:????????????????=??????????????????????????????=?
????????????????= ????????????????=
????????????????= ???????????????????= .
?
A
C
F
B
E
D
????3
?
????4
?
????2
?
????1
?
????5
?
活动1:如图,小方格的边长都是1,直线????????,????????被一组平行线????????,????????,????????所截,交点A,B,C,D,E,F都在格点上:
?
12
?
13
?
23
?
12
?
13
?
23
?
讲授新课
A
C
F
B
E
D
????3
?
????4
?
????2
?
????1
?
????5
?
活动2:当直线l4平移到如图所示的位置时,刚才的结论仍然成立吗?
算一算下列线段的比值:????????????????=??????????????????????????????=?
????????????????= ????????????????=
????????????????= ???????????????????= .
?
2
?
23
?
13
?
2
?
23
?
13
?
讲授新课
A
B
E
D
????3
?
????4
?
????2
?
????1
?
????5
?
活动3:当直线l5平移到如图所示的位置时,刚才的结论仍然成立吗?
算一算下列线段的比值:????????????????=??????????????????????????????=?
????????????????= ????????????????=
????????????????= ??????????????????????=
?
1
?
12
?
1
?
C
F
12
?
12
?
12
?
由此可知,当????????∥????????∥????????时,????????????????=????????????????,????????????????=????????????????,????????????????=????????????????.
?
讲授新课
一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
讲授新课
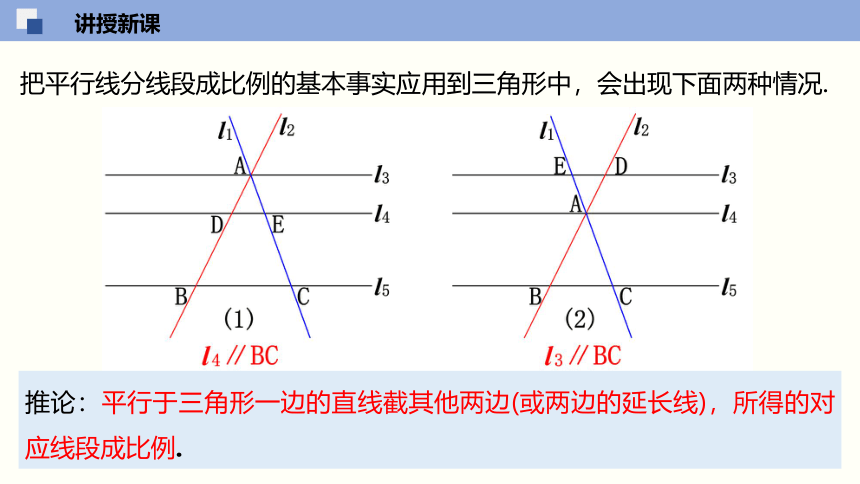
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
讲授新课
典例精析
【例】如图所示,在△ABC中,E,F,分别是AB和AC的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AE = 7, EB = 5 , FC = 4.
∴
讲授新课
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AB = 10 , AE = 6 , AF = 5.
∴
∴FC=AC – AF =
讲授新课
练一练
1、如图,已知l1∥l2∥l3,下列比例式中错误的是 ( )
A. B.
C. D.
D
A
C
E
B
D
F
l2
l1
l3
讲授新课
2、如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=52GC D.EG=2GC
?
【详解】∵DE∥FG∥BC,DB=4FB,∴????????????????=????????????????=31=3.故选B.
?
3、如图,直线l1//l2//l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为( )
A.2 B.3 C.4 D.103
?
【详解】解:∵直线l1∥l2∥l3,∴????????????????=????????????????.
∵AB=5,BC=6,EF=4,∴56=????????4.∴DE=103.故选:D.
?
当堂检测
A
B
C
D
E
1.已知:DE//BC, AB=15,AC=9,BD=4 .求AE的长.
解:
∵ DE∥BC,
AB AC
BD CE
∴
——
——
=
.(推论)
即
当堂检测
2. 如图,AD//BE//CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
?
【详解】解:∵AD//BE//CF,
∴ABBC=DEEF,即13=1.2EF,
∴EF=3.6,
∴DF=EF+DE=3.6+1.2=4.8,
故选B.
?
当堂检测
3、如图,在△ABC中,点D,E分别是AB和AC上的点,且DE//BC。若AE=1,AD=CE=2,则BD= ,AB= .
1
2
2
∵DE//BC,∴????????????????=?????????????????,则2????????=?12,
解得DB=4
?
∵DE//BC,∴????????????????=?????????????????,则2????????=?11+2?,
解得AB=6
?
当堂检测
4.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段????????的长是(????)
A.0.5 B.1 C.32 D.2
?
【详解】解:过点????作五条平行横线的垂线,交第三、四条直线,分别于????、????,根据题意得????????=2????????,
∵????????∥????????,
∴????????????????=????????????????=2,
又∵AB=3,
∴????????=12????????=32
故选:C
?
当堂检测
【详解】解:∵AE//DF,∴????????????????=????????????????,即6????????=32,
∴????????=4,∴????????=????????+????????=6+4=10,
∵????????//????????,∴????????????????=????????????????,即10????????=32,
∴????????=203,∴????????=????????+????????=323.
?
5.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE//AC、AE//DF,BD:AD=3:2,BF=6,求EF和FC的长.
课堂小结
可以发现,当l3∥l4∥l5时,有 , , , 等.
一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
课堂小结
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
谢 谢~
数学(浙教版)
九年级 上册
第4章 相似三角形
学习目标
1.理解平行线分线段成比例的基本事实及其推论;
2.掌握平行线分线段成比例的基本事实及其推论进行证明和计算;
温故知新
四条线段 a、b、c、d 中,如果 a:b=c:d,那么这四条线段a、b、c、d 叫做成比例的线段,简称比例线段.
比例的基本性质:
比例线段的概念:
等比的性质:
合比的性质:
如果ab=cd=…=mn (b+d+…+n≠0),那么a+c+…+m?b+d+…+n=ab.
?
如果????????=????????,,那么????+????????=????+????????, ?????????????=??????????????.
?
导入新课
下图是一架梯子的示意图,由生活常识可以知道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
讲授新课
知识点一 平行线分线段成比例概念
算一算下列线段的比值:????????????????=??????????????????????????????=?
????????????????= ????????????????=
????????????????= ???????????????????= .
?
A
C
F
B
E
D
????3
?
????4
?
????2
?
????1
?
????5
?
活动1:如图,小方格的边长都是1,直线????????,????????被一组平行线????????,????????,????????所截,交点A,B,C,D,E,F都在格点上:
?
12
?
13
?
23
?
12
?
13
?
23
?
讲授新课
A
C
F
B
E
D
????3
?
????4
?
????2
?
????1
?
????5
?
活动2:当直线l4平移到如图所示的位置时,刚才的结论仍然成立吗?
算一算下列线段的比值:????????????????=??????????????????????????????=?
????????????????= ????????????????=
????????????????= ???????????????????= .
?
2
?
23
?
13
?
2
?
23
?
13
?
讲授新课
A
B
E
D
????3
?
????4
?
????2
?
????1
?
????5
?
活动3:当直线l5平移到如图所示的位置时,刚才的结论仍然成立吗?
算一算下列线段的比值:????????????????=??????????????????????????????=?
????????????????= ????????????????=
????????????????= ??????????????????????=
?
1
?
12
?
1
?
C
F
12
?
12
?
12
?
由此可知,当????????∥????????∥????????时,????????????????=????????????????,????????????????=????????????????,????????????????=????????????????.
?
讲授新课
一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
讲授新课
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
讲授新课
典例精析
【例】如图所示,在△ABC中,E,F,分别是AB和AC的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AE = 7, EB = 5 , FC = 4.
∴
讲授新课
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
E
B
C
F
解: ∵EF∥BC,
∴
∵AB = 10 , AE = 6 , AF = 5.
∴
∴FC=AC – AF =
讲授新课
练一练
1、如图,已知l1∥l2∥l3,下列比例式中错误的是 ( )
A. B.
C. D.
D
A
C
E
B
D
F
l2
l1
l3
讲授新课
2、如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
A.EG=4GC B.EG=3GC C.EG=52GC D.EG=2GC
?
【详解】∵DE∥FG∥BC,DB=4FB,∴????????????????=????????????????=31=3.故选B.
?
3、如图,直线l1//l2//l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为( )
A.2 B.3 C.4 D.103
?
【详解】解:∵直线l1∥l2∥l3,∴????????????????=????????????????.
∵AB=5,BC=6,EF=4,∴56=????????4.∴DE=103.故选:D.
?
当堂检测
A
B
C
D
E
1.已知:DE//BC, AB=15,AC=9,BD=4 .求AE的长.
解:
∵ DE∥BC,
AB AC
BD CE
∴
——
——
=
.(推论)
即
当堂检测
2. 如图,AD//BE//CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=1.2,则DF的长为( )
A.3.6 B.4.8 C.5 D.5.2
?
【详解】解:∵AD//BE//CF,
∴ABBC=DEEF,即13=1.2EF,
∴EF=3.6,
∴DF=EF+DE=3.6+1.2=4.8,
故选B.
?
当堂检测
3、如图,在△ABC中,点D,E分别是AB和AC上的点,且DE//BC。若AE=1,AD=CE=2,则BD= ,AB= .
1
2
2
∵DE//BC,∴????????????????=?????????????????,则2????????=?12,
解得DB=4
?
∵DE//BC,∴????????????????=?????????????????,则2????????=?11+2?,
解得AB=6
?
当堂检测
4.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段AB=3,则线段????????的长是(????)
A.0.5 B.1 C.32 D.2
?
【详解】解:过点????作五条平行横线的垂线,交第三、四条直线,分别于????、????,根据题意得????????=2????????,
∵????????∥????????,
∴????????????????=????????????????=2,
又∵AB=3,
∴????????=12????????=32
故选:C
?
当堂检测
【详解】解:∵AE//DF,∴????????????????=????????????????,即6????????=32,
∴????????=4,∴????????=????????+????????=6+4=10,
∵????????//????????,∴????????????????=????????????????,即10????????=32,
∴????????=203,∴????????=????????+????????=323.
?
5.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE//AC、AE//DF,BD:AD=3:2,BF=6,求EF和FC的长.
课堂小结
可以发现,当l3∥l4∥l5时,有 , , , 等.
一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
课堂小结
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
谢 谢~
同课章节目录
